面向动态事件流的神经网络转换方法

张宇豪，袁孟雯，陆宇婧，燕锐，唐华锦，4

（1.四川大学 计算机学院，成都 610065；2.之江实验室 智能计算硬件研究中心，杭州 311100；3.浙江工业大学 计算机科学与技术学院，杭州 310023；4.浙江大学 计算机科学与技术学院，杭州 310027）

0 引言

近年来，事件相机作为一种生物启发的视觉传感器引起研究者广泛关注，其借鉴生物视网膜结构和功能机理，采用硅视网膜技术研制，具有高时域分辨率、高动态范围和低功耗等优势［1］。相较于传统相机，事件相机可以实时高效地捕捉场景变化，被用于多种计算机视觉任务，文献［2-5］中列举了一些常见的事件相机。由于传统方法较难适配事件相机输出的离散事件流数据格式，有效识别动态事件流模式成为计算机视觉领域的重要研究方向。

深度神经网络尤其卷积神经网络（Convolutional Neural Network，CNN）在图像识别等领域取得重大突破，被广泛应用于处理计算机视觉任务［6］。CNN 通常被用于处理基于帧的静态自然图像，虽然可以将事件流重构为图像帧［7］后再使用CNN 进行高效训练和识别，但在真实场景中通常需要对目标作出实时响应，事件流的重构处理会极大增加推理延迟。另一方面，CNN 采用大规模浮点乘累加运算，网络运行依赖大量算力，通常被部署于CPU 或GPU 等功耗较高的通用处理器，难以在现场可编程门阵列（Field Programmable Gate Array，FPGA）等专用硬件设备上高效实现。近年来，受大脑启发的脉冲神经网络（Spiking Neural Network，SNN）由于其更具生物合理性逐渐引起人们的兴趣［8］。相较于CNN，SNN 采用稀疏的脉冲序列进行通信，具有功耗低、计算量少等优势，已经在许多神经形态硬件上高效部署［9-13］。此外，SNN 采用事件驱动的计算范式，即脉冲神经元仅在输入脉冲到达时才更新内部状态，无脉冲或事件输入时神经元处于静息状态，更适于处理动态离散事件流数据。

在先前的研究工作中，部分研究人员基于视觉皮层［14］模型，提出使用事件驱动的Gabor 滤波器以及时间维度的最大池化方法以提取事件流特征，并训练单层SNN 分类器识别目标［15-17］；另一部分研究人员则采用时间表面的特征提取方法提取事件流特征［18-19］。但是，这些方法需要人工提取特征后再输入神经网络进行识别，并非端到端的计算模式，难以在专用硬件设备上有效部署。近年来，研究者基于代替梯度和时间反传方法直接训练深度SNN 以识别目标［20-22］。虽然获得了效果可接受的模型，但是在现有的通用处理器上直接训练深度SNN 用时较长、消耗资源较多，难以进行大规模高效训练。

为解决上述方法中深度SNN 在通用处理器上直接训练低效等问题，结合CNN 训练高效与SNN 低功耗、低延迟的优势，研究人员提出神经网络转换方法［23-24］。但是，他们识别的均为基于帧的静态自然图像，并未提出针对动态事件流模式的有效方案。文献［25］提出了可应用于事件流数据的转换方案，但与其他神经网络转换方法相同，转换后的网络中高精度权重等参数会占用大量的存储空间，难以被高效部署于资源有限的专用硬件设备。

本文提出一种面向动态事件流的神经网络转换方法并构建脉冲卷积神经网络（Spiking CNN，SCNN）。首先，将事件流数据重构以作为CNN 的输入，并使用量化激活函数和基于反向传播算法［26］的对称定点量化算法训练CNN；其次，在转换过程中采用脉冲计数等价原理以更好地适应数据的稀疏性；最后，将训练好的网络参数映射到SCNN 中。实验结果表明，所提出的SCNN 可以准确识别事件相机输出的事件流模式，降低网络转换的准确率损失。此外，网络参数均为定点数，易于在硬件上高效实现。

1 神经网络转换方法

1.1 人工神经元模型

人工神经元通过乘累加运算并使用非线性激活函数计算输出激活。如图1（a）所示，网络前馈过程计算如下：

其中：al为神经网络第l层神经元的输出激活向量；Wl-1为第l-1 层神经元与第l层神经元的突触连接权重矩阵；bl为第l层神经元的偏置向量。f(·)为非线性激活函数，最常使用的是线性整流函数（Rectified Linear Unit，ReLU）：

如上所述，传统深度神经网络通常用于处理静态自然图像，网络输入输出激活均为实数值，并且运行依赖大量算力，难以被高效部署于资源有限的专用硬件设备。

1.2 脉冲神经元模型

脉冲神经元具有丰富的动力学特性，通常使用微分方程对神经元动力学进行建模，常见的脉冲神经元模型有霍奇金-赫胥黎（Hodgkin-Huxley，HH）模型［27］、Izhikevich 模型［28］以及泄露聚集-发放（Leaky Integrate-and-Fire，LIF）模型［29］等。如图1（b）所示，相较于人工神经元，脉冲神经元的计算范式更适于处理动态离散事件流数据。为了计算高效且满足神经网络转换原理，脉冲神经元采用聚集-发放即IF 神经元模型：

其中：v为脉冲神经元膜电位；wi为第i个突触前脉冲神经元与该神经元的连接权重；n为突触前神经元数量；si(t)为t时刻突触前神经元的输入脉冲，取值为0 或1。

当突触后神经元膜电位累积达到阈值ϑ时，神经元发放脉冲且膜电位复位，如图2 所示。在实际操作中，通常将微分方程转化为离散迭代形式以进行网络前馈计算：

其中：dt为SNN 运行的时间步或时间分辨率（默认为1 ms）。

1.3 神经网络转换原理

神经网络转换方法的主要思想是脉冲神经元的脉冲发放频率与人工神经元的激活值等价，通常使用频率编码方式将输入激活编码为脉冲序列，即脉冲序列的频率值作为网络有效信息。单个脉冲神经元的脉冲发放频率可定义为：

其中：r为脉冲神经元的频率值；c为脉冲随时间的累积值即脉冲计数；T为脉冲发放时间窗；rmax为最大发放频率。

结合式（4）及神经元脉冲发放机制可得IF 神经元的输入脉冲计数与输出脉冲计数的关系为：

由式（1）和式（7）可知，当脉冲发放时间窗较大时，通过设置人工神经元偏置项为0 及脉冲神经元发放阈值为1，可以实现人工神经元激活值与脉冲神经元发放频率值近似等价（本文后续公式及方法均采用上述参数设置）。

2 面向事件流的网络转换方法

传统神经网络转换方法使用静态自然图像作为输入，因此需要对像素值采用频率编码的方式转化为脉冲序列，但这种重编码方案并不适用于具有时空特性的动态离散事件流数据。此外，由人工神经网络与脉冲神经网络的计算差异性可知，网络转换会存在准确率损失，并且网络通常采用大规模浮点参数，占用大量的存储空间和资源，难以在资源有限的神经形态硬件等专用硬件设备上高效部署。

为解决上述问题，本文提出一种面向动态事件流的神经网络转换方法并构建SCNN，转换流程如图3 所示。向量a、c和s的含义如前所述，其中CNN 传输的是激活向量a，SCNN传输的是脉冲向量s。

2.1 事件流重构

事件流数据的每个事件可以采用地址事件表示（Address-Event Representation，AER）格式表征［30］。AER 具体形式为（x，y，t，p）的四元组，其中x、y表示事件的像素位置坐标；t为事件产生的时间戳；p为事件所属极性，根据场景亮度变化分为由亮到暗（-1）和由暗到亮（+1）两种极性，如图4（a）所示。为匹配CNN 的输入数据格式，本文使用计算简便且高效的重构方案将动态事件流数据重构为静态图像帧数据。

首先，将事件的四维数据（x，y，t，p）转化为传统图像的三维张量，事件的像素位置对应传统图像的空间位置，事件所属极性对应传统图像的颜色通道。其次，根据事件流的稀疏程度确定转换后SCNN 的时间分辨率，根据时间分辨率可以将数据切分为多个三维张量图像，如图4（b）所示。最后，将对应像素位置的脉冲事件数据随时间累积为静态图像帧数据，如图4（c）所示。

2.2 量化激活函数

如1.3 节所述，通过设置神经元的参数可以实现两类神经元输出近似等价。但是，无论采用哪种等价原理（计数等价al⇔cl或频率等价al⇔rl），均会产生与成正比的损失。虽然当时间窗很大时采用频率等价造成的损失几乎为零，但计算量和运行时延会大幅增加。此外，随着网络层数的增多，两种等价原理的转换损失均呈指数型增长以致不可忽略。实验结果（见3.2.1 节）表明，对于稀疏的事件流数据，计数输入比频率输入的网络识别准确率更高，因此本文采用计数等价原理。

为了降低网络转换损失，本文采用Sorbaro等［25］提出的方案，该方案可以减小连续激活值被转换为有限数量脉冲时导致的激活误差。引入量化激活函数QReLU 代替传统ReLU 激活函数：

将式（8）代入式（1）可得网络前馈计算为（假设输出为正值且偏置项为0）：

其中：为激活向量取整后的小数向量。研究表明，由于QReLU 函数输出值均为整数，采用频率等价会导致网络训练失效，再次验证计数等价原理的有效性。结合式（6）可得网络转换损失为（假设输入完全等价无损且采用1.3 节参数设置）：

与均为小数部分，因此存在即εl≈0，表明人工神经元的激活值几乎可与脉冲神经元的脉冲计数完全等价。相较于传统网络转换方法，使用该激活函数可进一步降低网络转换损失且网络加深后转换损失可忽略不计。此外，Sorbaro等［25］表明使用该激活函数的网络可以在训练期间意识到离散化误差并自动调整参数以解释该误差，因此原始网络由于取整函数导致的准确率损失可忽略不计。

2.3 参数量化

网络参数必须为定点数才能在专用硬件设备上高效部署，为此研究人员提出二值权重量化算法Binary-Connect［31］。研究表明噪声权重即离散化权重提供了一种正则化形式，并且与深度学习的优化算法兼容，因此可以在确保识别准确率的同时使用二值化权重降低参数存储量，减少硬件资源。谷歌团队进一步提出非对称量化感知训练方法，以解决小模型训练后直接量化方法的准确率损失较大的问题［32］。在此基础上，本文改进了一种参数对称定点量化方法。

借鉴Binary-Connect 的权重二值化操作（即利用权重符号所构成的二值化权重进行网络前馈和反传计算），本文采用对称定点化权重进行有效训练：

其中：W为原始高精度浮点权重矩阵；Wq为量化后的定点权重矩阵；round(·)为四舍五入取整函数；α为量化尺度。若采用8 bit 定点量化，则α取127。注意，训练后的权重精度变为1，网络推理时可直接使用定点数（即乘以α）替换。网络训练过程中其他操作与Binary-Connect 相同，伪代码如算法1所示。

算法1 对称定点量化算法。

输入 输入激活向量a0，各层初始浮点权重矩阵W，网络层数L，训练学习率η。

输出 训练完成的量化权重矩阵Wq。

3 实验与结果分析

3.1 实验设计

3.1.1 数据集

本文在3 个公开的事件相机数据集上对所提算法进行实验验证，分别为基于异步时间图像传感器（Asynchronous Time-based Image Sensor，ATIS）［3］采集的N-MNIST 数据集［33］和动态视觉传感器（Dynamic Vision Sensor，DVS）［2］采集的POKER-DVS 数据集［34］及MNIST-DVS 数据集［34］。

3.1.2 网络架构

不同数据集使用的网络架构如图5 所示。图5 中32C3表示含有32 个3×3 卷积核的卷积层；128F 表示含有128 个输出神经元的全连接层，其余同理。由于N-MNIST 数据集和POKER-DVS 数据集尺寸较小，网络可采用较为简单的架构。对于MNIST-DVS 数据集，其数据尺寸为128×128，使用的网络架构相对复杂；同时，该数据集通过预处理已消除极性，输入通道数为1。

3.1.3 实验平台

实验采用的计算机CPU 为Intel Core i9-10900X，频率为3.70 GHz；GPU 为NVIDIA GV102，显存为11 GB。软件仿真环境采用Ubuntu 18.04.5 的操作系统，编程语言为Python 3.8.8，深度学习开发框架为PyTorch 1.8.0，GPU 加速工具为CUDA 10.1。

3.1.4 参数设置

本文使用多分类任务常用的交叉熵损失以及Adam 优化算法训练CNN，学习率初始化为0.001 且随迭代次数衰减。实验设定SCNN 最后一层脉冲神经元无阈值限制，即依据输出脉冲神经元的膜电位判断样本数据所属类别（即膜电位最高的神经元所属类别）。

如2.1 节所述，依据事件流的稀疏程度确定时间分辨率。POKER-DVS 数据集的数据较为密集，因此设定该数据集的时间分辨率为0.1 ms，其余数据集为1 ms。

3.1.5 评估指标

实验采用的主要评估指标是平均准确率Acc（accuracy），即分类正确的样本数占样本总数的比例，具体计算公式如下：

其中：Ncorrect为分类正确的样本数量，Ntotal为样本总数。此外，实验还采用余弦相似度评估特征图展平后的特征向量之间的差异性，具体计算公式为：

其中：x和y为两个特征向量，x·y为向量内积运算，‖ ‖· 为向量的模长。由于特征值均为正值，因此余弦相似度的取值范围是［0，1］。余弦相似度值为1 表明两个向量方向完全相同，0 表明两个向量完全独立，值越大表明向量之间的相似性越高，差异越小。

3.2 实验结果

3.2.1 时间窗与等价原理选取

首先采用不同时间窗及数据输入格式（即不同等价原理）训练CNN，识别结果见图6。由于事件流数据的稀疏性，与脉冲计数输入相比，频率输入的激活值较小，CNN 识别准确率较低，表明计数等价原理更适用于稀疏事件流数据。

另一方面，不同时间窗的实验结果显示，时间窗取值较小时，网络识别准确率较低；随着时间窗的增大，识别准确率逐渐提高，这表明网络需要积累一定事件信息才能区分不同模式。值得注意的是，N-MNIST 数据集上网络识别准确率随着时间窗的增大先提高后降低，可能是由于噪声事件的过量积累导致不同类别样本之间的差异减小，识别准确率有所下降。综上所述，为了计算高效且确保网络的识别准确率，不同数据集选用不同的时间窗以进行后续实验（N-MNIST 数据集的时间窗为50，POKER-DVS 数据集和MNIST-DVS 数据集为90）。

3.2.2 激活函数评估

为了验证QReLU 激活函数对识别准确率的影响，本文分别使用带有不同激活函数的网络进行实验，实验结果如表1 所示，每类实验分别运行10 次后取平均值。实验结果显示，虽然采用ReLU 函数的网络可以训练出准确率较高的CNN，但转换后的SCNN 准确率较低，转换损失较大。然而，采用QReLU 函数的网络在CNN 识别准确率相当的情况下，可以得到识别效果较好的SCNN，准确率分别提高了0.29、8.52 和3.95 个百分点，转换损失分别降低了21.77%、100.00%和92.48%。此外，由于N-MNIST 数据集的样本录制过程较为稳定，转换损失降低效果并不明显，而POKERDVS 与MNIST-DVS 数据集的转换损失降低效果较为明显（由于POKER-DVS 数据集的样本数量较少，识别结果较不稳定，相较于CNN 的识别准确率，SCNN 的识别准确率反而提高）。

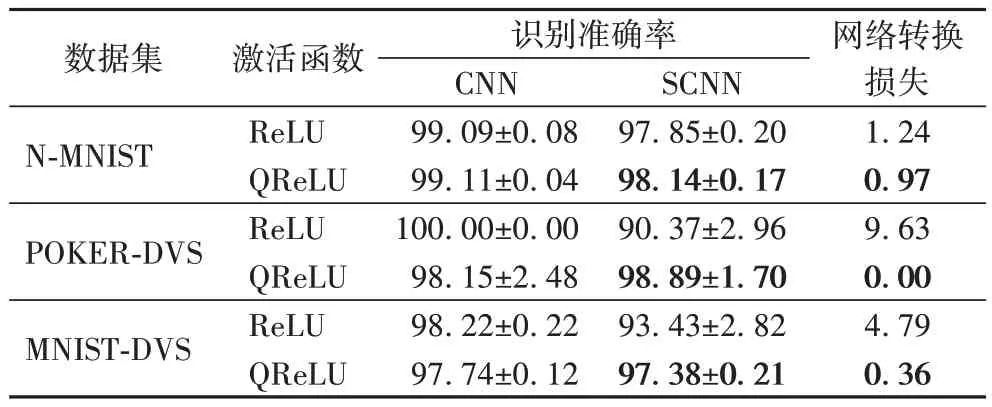
表1 采用不同激活函数的网络识别准确率 单位：%Tab.1 Network recognition accuracies with different activation functions unit：%

实验还对比了采用不同激活函数的网络提取的卷积特征图之间的差异，选用原始卷积特征图（最后一层卷积输出）与相应脉冲卷积特征图的平均余弦相似度作为评估指标，如表2 所示。实验结果表明，对于POKER-DVS 与MNIST-DVS数据集，网络采用QReLU 函数时特征图之间的平均余弦相似度较大，说明该函数可以缩小脉冲卷积特征图与原始卷积特征图之间的差异。对于N-MNIST 数据集，采用QReLU 函数网络的特征图余弦相似度比采用ReLU 函数的网络低，可能是由于该数据集录制结果较为稳定，特征图之间的差异较小。

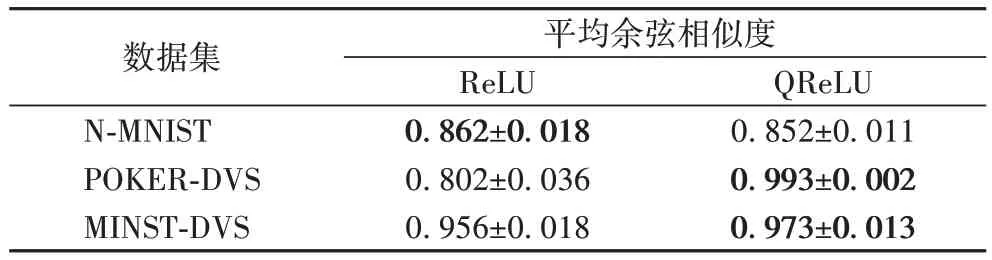
表2 采用不同激活函数的网络特征图的平均余弦相似度Tab.2 Average cosine similarities of network feature maps with different activation functions

3.2.3 参数量化评估

本文比较了传统高精度SCNN 与所提出的量化SCNN 的参数存储量，如表3 所示。所有脉冲神经元的发放阈值为统一值，增加的存储量可以忽略不计。因此，定点量化（8 bit）网络相较于传统高精度（32 bit）网络可以有效节省约75%的存储空间，更适用于资源受限的专用硬件设备。

表3 高精度SCNN与量化SCNN的参数存储量对比Tab.3 Parameter storage comparison of high-precision SCNN and quantized SCNN

同时，实验比较了训练中量化与训练后量化的识别准确率，如表4 所示（对比实验所用网络采用QReLU 激活函数）。结果表明，与训练后对参数直接进行量化的方法相比，本文的训练中定点量化方法可以提升一定的识别准确率并降低转换损失，并且网络训练过程中的权重参数具有定点化精度，有助于在硬件上实现训练过程。

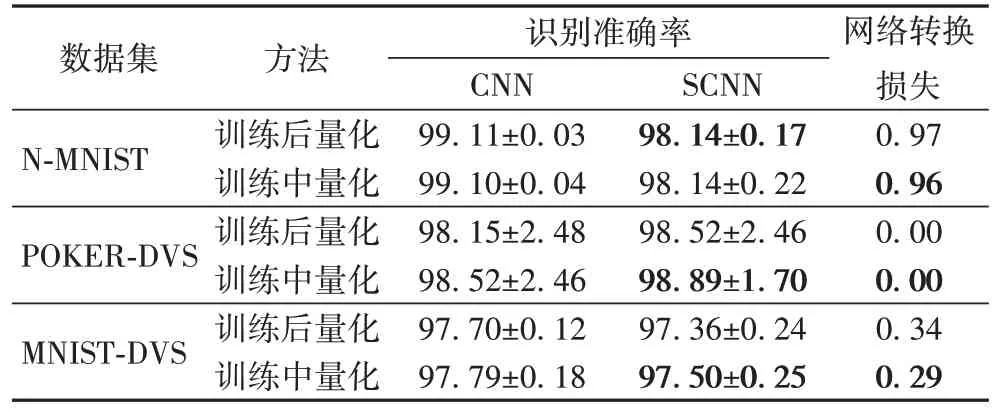
表4 不同量化方法的识别准确率对比 单位：%Tab.4 Recognition accuracy comparison of different quantization methods unit：%

3.2.4 转换方法对比

对比现有神经网络转换方法与本文提出的网络转换方法（无量化和量化）的识别准确率，如表5 所示。结果表明，本文提出的转换方法生成的SCNN 与基于权重归一化技术的转换方法［24］生成的SCNN 识别准确率相当，并且转换损失在N-MNIST 和MNIST-DVS 数据集上分别降低了6.79%和46.29%。另一方面，本文选用的计数等价原理可以将CNN权重直接映射到SCNN，无需额外的权重归一化操作，转换流程更加简便高效。此外，本文的量化SCNN 的前馈和反传计算均采用定点参数，易于在专用硬件设备上高效实现。

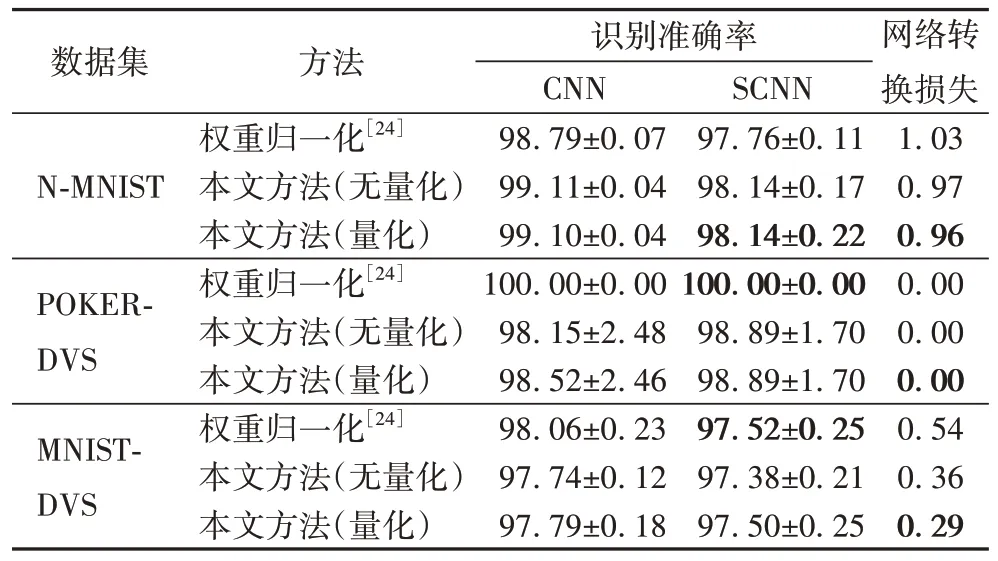
表5 不同转换方法的识别准确率对比 单位：%Tab.5 Recognition accuracy comparison of different conversion methods unit：%

4 结语

本文提出一种面向动态事件流的神经网络转换方法并构建相应的SCNN。该方法可以结合CNN 与SNN 的优势，适配动态离散事件流数据格式并有效量化网络参数，解决深度SNN 在通用处理器上训练低效且难以在专用硬件设备上高效部署等问题。实验结果表明，所提出的转换方法生成的SCNN 可以有效识别事件流模式并降低网络转换损失。同时，定点参数可以节省大量的存储空间，有助于深度SNN 在神经形态硬件等专用硬件设备上高效实现。

未来主要计划在以下几个方面对该工作进行改进和完善：

1）网络可扩展性：选用更深层且更复杂的网络结构（包括偏置项及最大池化层等），并在更困难的事件流识别任务上进行实验验证。

2）网络硬件部署：考虑后续的硬件适配及优化工作，将网络部署于FPGA 或神经形态硬件等专用硬件设备。