精确估计下的多智能体系统漏斗复合控制

李枝强 ,刘 洋 ,周 琪 ,鲁仁全

(1.广东工业大学广东省智能决策与协同控制重点实验室,广东广州 510006;2.山东交通学院航运学院,山东威海 264200)

1 引言

近年来,多智能体系统协同控制因其通信成本低、灵活性与鲁棒性高等特点,在卫星集群、无人车跟踪、移动机器人等领域得到了广泛应用[1-4].作为协同控制的基本问题,一致性跟踪控制受到了国内外专家学者的广泛关注,并取得了大量研究成果[5-8].实际系统大多是本质非线性的,而神经网络(neural network,NN)作为一种处理非线性的有效手段,广泛应用于控制器设计中[9-16].其中,文献[12]采用NN逼近严格反馈系统的未知非线性函数,并基于动态面技术设计了自适应NN控制器,解决了传统反步法的“计算爆炸”问题.文献[13]针对一类具有周期扰动的纯反馈非线性系统,提出了自适应NN控制方法,放宽了未知非仿射函数的有界条件,并消除了非仿射函数可微的限制.文献[14]研究了一类非严格反馈系统的自适应NN控制问题,利用系统边界函数的单调性和径向基NN的结构特征,克服了非严格反馈结构带来的设计困难.文献[15]提出了一种自适应NN容错控制方法,利用NN逼近大系统的非线性互联项,并设计了扰动观测器对逼近误差、未知死区和外部扰动组成的复合扰动进行估计.文献[16]将NN扩展到多智能体系统的研究中,设计了NN状态观测器,解决了高阶非线性多智能体系统的状态不可测问题.然而,文献[9-16]采用的传统NN不能准确逼近未知非线性.为了得到更好的逼近效果和期望性能,文献[17]提出了一种复合NN动态面控制方法,在权值更新律的设计中引入预测误差,实现了对未知非线性函数的精确逼近.文献[18]采用文献[17]提出的思想,设计了基于NN和扰动观测器的估计模型,解决了具有时变扰动的未知非线性系统自适应控制问题.文献[17-18]将复合自适应律的设计思想引入简单系统中,得到了准确逼近的效果.

系统受物理器件和外界条件的限制,在控制过程中往往需要对跟踪误差进行约束,从而保证系统安全稳定运行.漏斗控制作为一种有效的约束方法,可以较好地调节闭环系统稳态和瞬态响应.目前,针对漏斗控制的研究已取得了丰硕的成果[19-24].其中,文献[22]首次提出了漏斗控制设计思想,并通过简单的误差反馈控制,使跟踪误差满足规定约束.文献[23]将漏斗误差变换与动态面技术相结合,提高了严格反馈系统的输出性能.文献[24]改进了漏斗误差变换,解决了文献[23]中跟踪误差为零时存在的不可微问题.需要指出的是,上述研究仅能得到渐近稳定的结果,而实际工程控制中往往需要闭环系统在有限时间内达到稳定状态.为此,文献[25]针对非仿射非线性系统,设计了自适应有限时间漏斗控制器,使闭环系统中的信号均为半全局实际有限时间有界的.文献[26]针对具有未知输入约束的永磁同步电机系统,提出了一种有限时间NN漏斗控制方法,使跟踪误差有限时间稳定且约束在规定的漏斗边界内.但文献[25-26]提出的有限时间都受限于系统初始条件和设计参数,且设计过程相对复杂.

鉴于以上分析,本文研究一类具有未知非线性和时变扰动的多智能体系统一致性跟踪问题,设计基于精确估计的预设有限时间(preassigned finite-time,PFT)漏斗复合控制器.不同于文献[25-26]的结果,本文提出的PFT漏斗控制方法保证跟踪误差收敛时间的独立性和灵活性,并且设计过程简单.此外,尽管文献[18]在文献[17]的基础上处理了外界扰动对系统的影响,但是它们的研究对象均为简单的非线性系统,无法直接应用到复杂的多智能体系统中,而本文结合智能体间的拓扑结构与权值复合更新律的设计思想,建立复合估计模型来提高逼近精度,进而增强多智能体系统的鲁棒性.

2 预备知识与问题阐述

2.1 代数图论

本文采用图论描述智能体间的通信拓扑,定义有向图G=(V,E,A).其中,V=(v1,v2,···,vN)为N个智能体的非空集合,E ⊆V ×V为智能体边的集合,(vi,vj)∈E表示智能体i接收到智能体j的信息.智能体i的邻接节点集合表示为Ni={vj ∈|(vi,vj).定义权重邻接矩阵为A=[ai,j]∈RN×N,如果(vi,vj)∈E,那么ai,j ＞0;否则ai,j=0.假设拓扑图中不存在自环,即ai,i=0,∀i ∈V.定义节点i的入度矩阵为bi=,入度对角矩阵R=diag{b1,b2,···,bN},则图G的拉普拉斯矩阵为L=R-A.定义H=diag{a1,0,a2,0,···,aN,0},如果节点i能接收到领导者0的信息,则ai,0＞0;否则,ai,0=0.

引理1[5]如果存在一条路径能够从根节点0到达所有其他节点,那么称有向图G具有一个生成树,则矩阵L+H是非奇异的.

假设1[6]领导者的信号y0只能被部分智能体直接获取.且y0已知,y0及其导数均为连续有界的.

2.2 系统描述

本文研究的多智能体系统包含N个跟随者,第i个跟随者可描述为一类具有未知非线性与时变扰动的ni阶严格反馈系统

2.3 漏斗控制

漏斗控制通过引入时变的控制增益ϱ(t)达到控制目的,文献[22]将漏斗控制的控制输入定义如下:

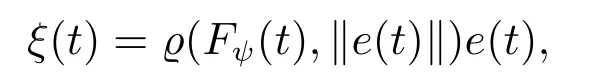
其中:Fψ(t)为漏斗边界;‖e(t)‖为跟踪误差的欧几里得范数.

控制增益ϱ(t)可选择为

注1根据文献[19-26]中采用的漏斗边界可知,其需在时间趋于无穷时收敛于ρ∞.相比之下,本文所设计的PFT漏斗边界具有更好的暂态性能,因其可在有限时间Ti收敛到提前设定的界内,这也体现了设计方法的灵活性.

3 控制器设计和稳定性分析

3.1 预设有限时间漏斗复合控制器设计

本节设计了一种PFT漏斗复合控制器,使跟踪误差约束在PFT漏斗内,并保证闭环系统中的所有信号均为有界的.基于NN的逼近特性,系统(1)可转换为如下形式:

3.2 稳定性分析

本节采用Lyapunov函数对多智能体系统进行稳定性分析.

定理1在假设1和假设2成立的条件下,考虑虚拟控制信号(17)(26)(32),实际控制器(36),滤波补偿信号(19)(28)(33)(37),NN权值的复合更新律(21)(30)(34)(38),如果跟踪误差ei,1(t)的初始条件满足ei,1(0)＜Fψ,i(0),则多智能体系统(1)的所有信号均为有界的,且跟踪误差ei,1(t)约束在规定的PFT漏斗边界内.

证选取Lyapunov函数为

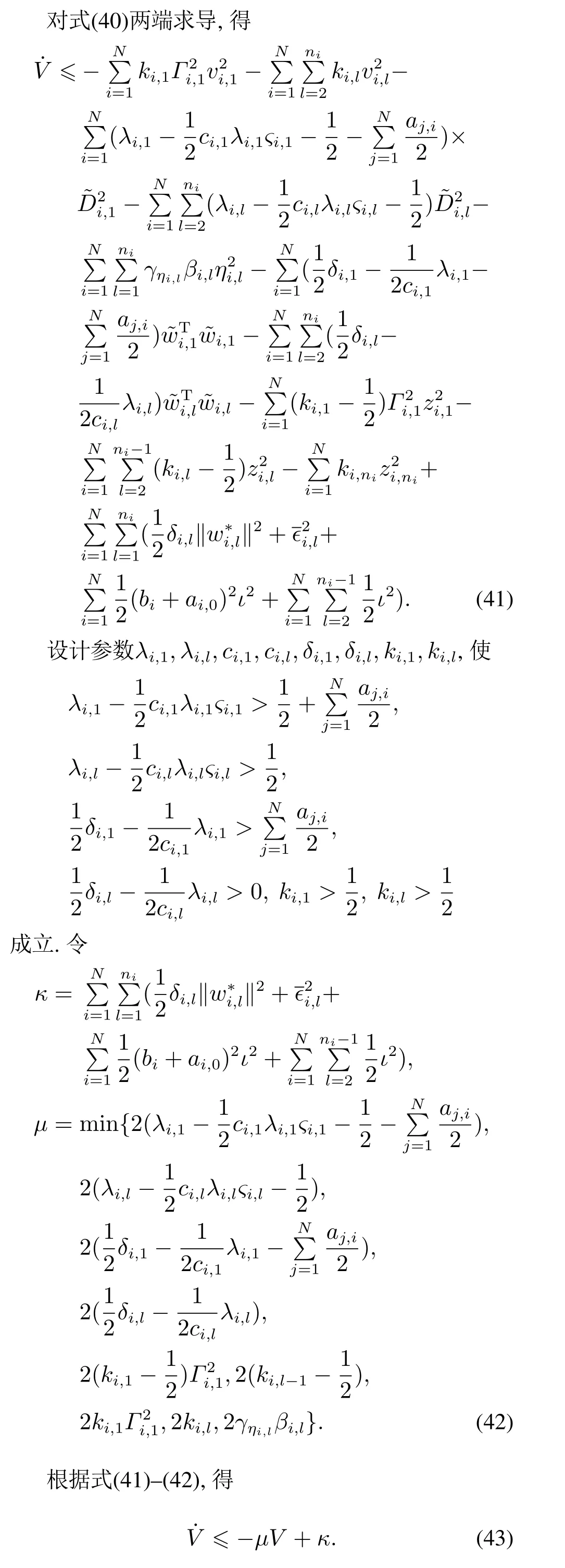
由式(43),得

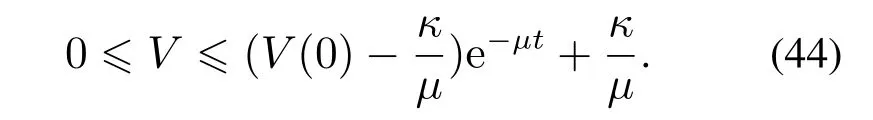
从式(44)可知,当t →∞时,V →(κ/μ).可以证明Lyapunov函数(40)中的所有信号均为有界的.并由式(6)可得误差|ξi,1|和|ei,r|是有界的,令

其中边界ϑ的大小与设计参数有关.

根据式(45),得

将式(2)代入式(46),得

由式(47)得

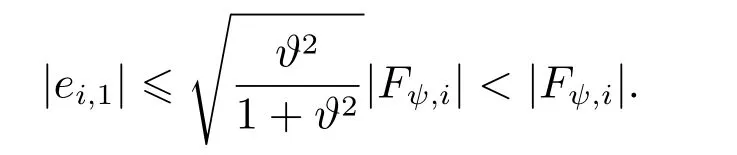
则多智能体的跟踪误差约束在PFT漏斗边界内,并且通过调整设计参数可以使跟踪误差任意减小.

证毕.

4 数值仿真

为验证所提出控制方法的有效性,本节考虑的多智能体系统由4个跟随者和1个领导者组成,每个跟随者为具有时变扰动的二阶严格反馈非线性系统

多智能体通信拓扑见图1.其中领导者的输出信号为y0=sint.假设所有边的权重都为1,跟随者与领导者之间的连接权重为H=diag{1,0,1,0},选择邻接矩阵A与拉普拉斯矩阵L如下:

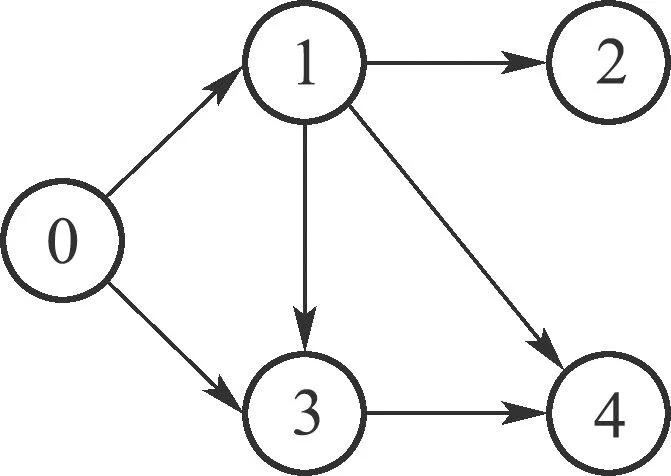
图1 通信拓扑图Fig.1 Communication topology

在仿真中,初值设置为xi,1(0)=(0)=[0.1 0 0.1 0],xi,2(0)=(0)=[0 0 0 0],si,1(0)=[0.9 1 0.9 1],si,2(0)=[0.1 0 0.1 0],(0)=(0)=[0 0 0 0].将NN初始权值设为0,其中xi,1,xi,2的中心点在[-1,1],[-2,2]均匀间隔,对fi,1选择NN节点数为ςi,1=7,对fi,2选择NN 节点数为ςi,2=25.选取设计参数的值为ρi,0=1,ki,1=ki,2=10,ρi,Ti=0.02,Ti=0.1,τi,1=0.005,βi,1=βi,2=1,γi,1=γi,2=1,γηi,1=γηi,2=50,δi,1=δi,2=10,λi,1=λi,2=10.

仿真结果如图2-6所示.图2为跟随者yi的跟踪效果图,在较短的时间实现了一致性跟踪.图3为跟踪误差,由图3(a)可知,漏斗控制使跟踪误差约束在给定的漏斗边界内;对比图3(a)和3(b)可看出,不具有PFT漏斗控制的跟踪误差渐近稳定且稳态误差接近0.02,而加入PFT漏斗控制后的跟踪误差在预设时间0.1 s前稳定且稳态误差小于0.0001,因此,PFT漏斗控制显著减小了一致性跟踪的稳态误差,并保证误差在预设时间内收敛.图4-5给出了未知非线性和时变扰动的逼近效果,由图4(a)和5(a)可知,采用NN和扰动观测器的复合估计模型,能精确估计多智能体系统的未知非线性和时变扰动;与图4(b)和5(b)的传统NN逼近方法相比,本文设计的复合更新率使估计模型具有更精确的逼近效果.图6为控制器输入ui,系统稳定后控制输入均小于3,表明该控制器能耗较低、性能良好.

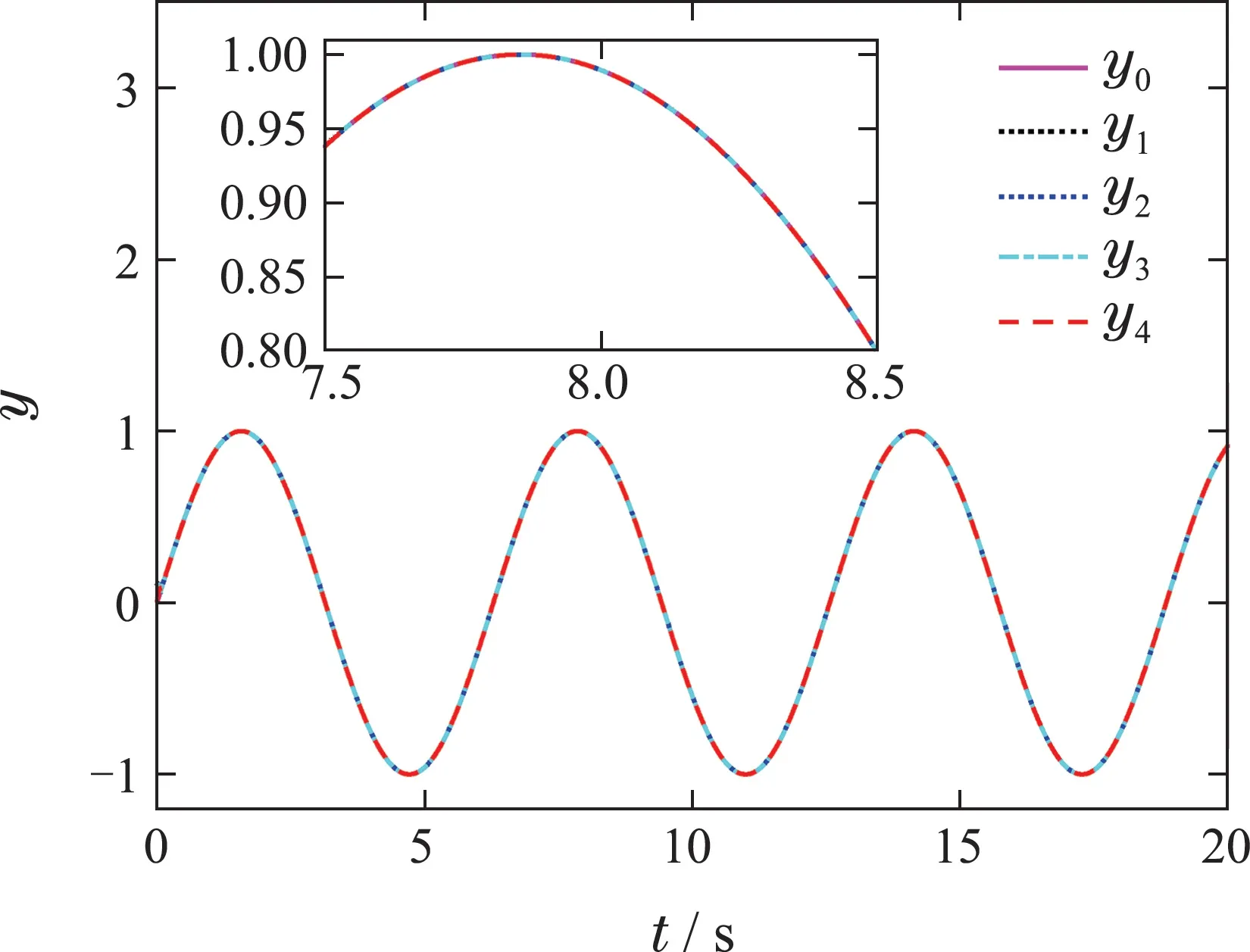
图2 参考信号y0和输出信号yiFig.2 Reference signal y0 and output yi

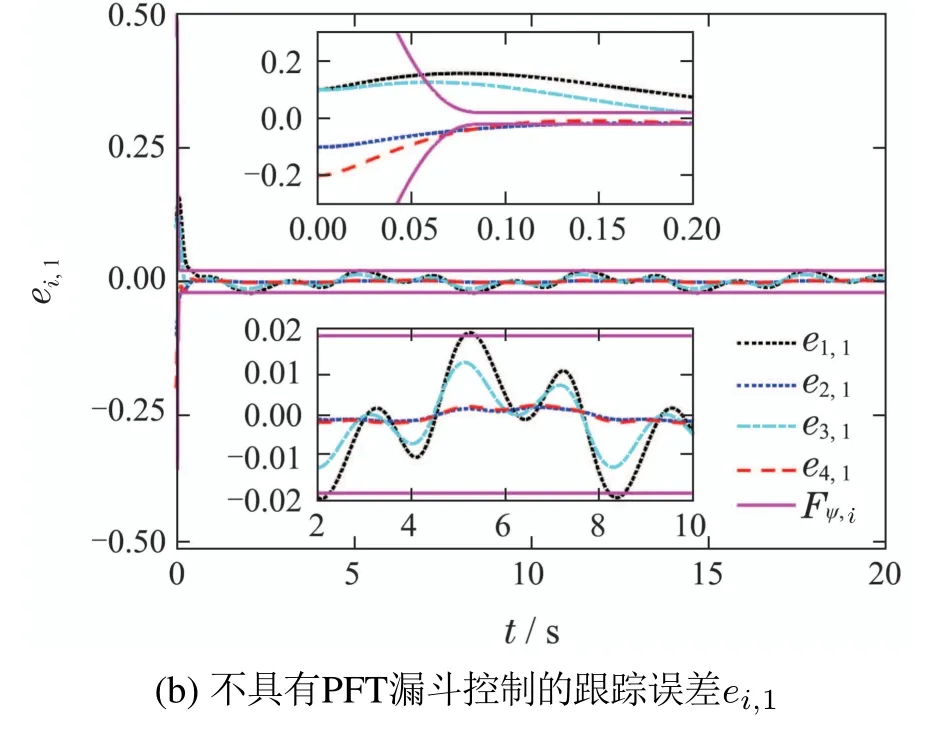
图3 跟踪误差ei,1Fig.3 Tracking errors ei,1

图4 两种估计(fi,1+di,1)的方法Fig.4 Two estimation methods of(fi,1+di,1)

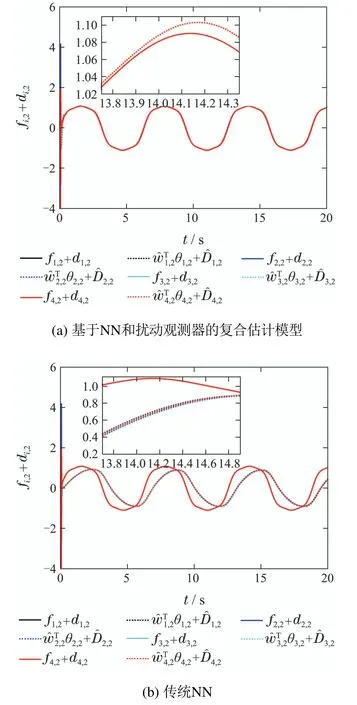
图5 两种估计(fi,2+di,2)的方法Fig.5 Two estimation methods of(fi,2+di,2)

图6 控制信号uiFig.6 Control signal ui

5 结论

本文研究了具有未知非线性和时变扰动的多智能体系统一致性跟踪问题.在控制器设计过程中,引入了PFT漏斗控制方法,使跟踪误差约束在PFT漏斗内,达到了预设时间收敛的目标.建立了基于NN和扰动观测器的复合估计模型,精确估计了多智能体系统的未知非线性和时变扰动.并结合动态面技术设计了基于精确估计的PFT漏斗复合控制器,实现了对领导者的一致性跟踪.通过仿真验证了该方法的有效性.在未来研究中,考虑将该方法应用于更复杂的环境中.