网络攻击下一类非线性切换多智能体系统的安全自适应控制
李占杰马亚静岳 东
(1.南京邮电大学先进技术研究院,江苏南京 210003;2.南京邮电大学物联网学院,江苏南京 210003;3.南京邮电大学江苏省宽带无线通信和物联网重点实验室,江苏南京 210003)
1 引言
由于多智能体系统相关理论在电力网络、无人驾驶汽车和智能交通等工程领域中被广泛应用,近年来多智能体系统的控制问题吸引了科研工作者的广泛关注,并取得了许多重要研究成果[1-4].在多智能体一致性控制研究中,智能体之间需要进行通信信息传输,并且信息的传输通常需要借助一些无线网络传播媒介[5-7].众所周知,网络信息传输容易受到恶意对手的攻击[8-9].敌人可以监视系统状态信息并将假数据注入控制系统[10-11].例如,在电力传输系统中,敌人可以通过入侵远程终端单元发动攻击.因此,对抗恶意攻击的多智能体安全一致性控制是一个重要且广受关注的研究课题.文献[12-13]研究了在多种网路攻击下多智能体系统的领导-追随安全控制问题.针对异构电池储能系统,文献[14]解决了拒绝服务攻击发生时的分布式安全二次控制问题.
注意到上述安全控制结果基于一个共同假设,即系统控制方向是已知的.当研究控制方向未知的多智能体安全控制问题时,这些控制方法将不再适用.针对此问题,一个有效的方法就是利用Nussbaum型函数方法[15-16].文献[17-18]利用Nussbaum函数解决了具有未知方向的非线性多智能体系一致性问题.针对未知的状态反馈增益,文献[19-20]借助Nussbaum函数研究了在传感器攻击下的非线性信息物理融合系统安全控制.然而,应当强调的是上述结果[17-20]构造了多个自适应律以解决系统和攻击带来的不确定性,但这些自适应律却依赖于智能体的个数和每个智能体的阶数,这不可避免地增加了系统分析和设计复杂性.另一方面,众所周知许多自然或人造动态系统具有内在的切换特征,例如:网络控制系统、自动驾驶汽车等[21-24].文献[25-26]表明即使所有子系统都是稳定的,整个切换系统也可能是不稳定的.此时,前述非切换控制结果很难用于解决具有切换动态的非线性多智能体系统控制问题.据作者所知,由于未知控制方向、未知参数、不确定网络攻击和切换动态相互耦合带来的困难,非线性切换多智能体的安全控制问题尚未得到充分研究.
针对一类非线性切换多智能体系统,本文旨在提出自适应安全一致性协议,保证智能体输出在网络攻击下达到渐近一致性,其主要贡献可总结为:1)解决在网络攻击下具有未知控制方向的切换多智能体系统的安全控制问题.在切换情形下,提出一系列辅助变量处理网络攻击的影响;2)构造一个不依赖智能体个数和智能体阶数的自适应参数解决系统中耦合不确定因素.与文献[17-20]智能体依赖多自适应参数相比,所提出方法极大降低了系统的复杂性.
2 问题描述
考虑一类非线性切换多智能体系统,其第j个智能体的数学模型描述如下:



3 主要结果
3.1 自适应一致性协议设计
设计过程包含n个步骤.
步骤1首先,构造以下辅助变量:
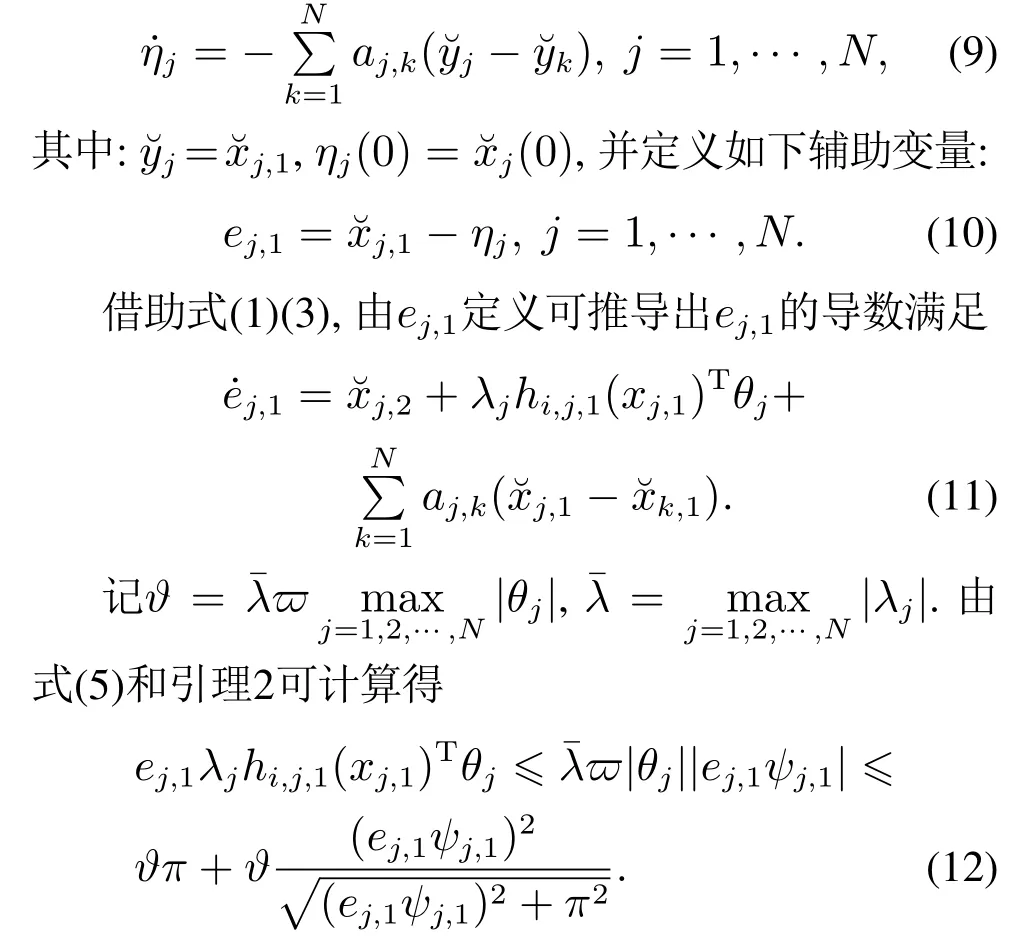



以及如下自适应律:

并可以计算得到
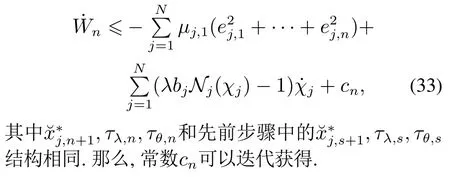
注2由于系统状态xj,s被传感器攻击损坏,因此直接利用状态xj,s信息设计虚拟协议和真实协议将无法实现.为了解决此问题,在迭代过程中,采用侵入状态构造一组辅助变量ηj和ej,s.为了成功构造辅助变量,每个智能体的所有的子系统共用一个虚拟协议.由此,可以处理未知的网络攻击和切换之间的耦合影响.
注3未知系统参数θj以及未知攻击权重δj不可避免的导致一些未知参数.在现有结果中,针对非切换系统,文献[17-20]引入了多个自适应参数来补偿这些未知量,并且自适应参数的数目与智能体的数量和每个智能体的阶数相关.显然,智能体数量过多或每个智能体阶数过高将导致十分复杂的闭环系统.本文设计过程中仅需要构造两个自适应律(32)就可以补偿未知参数,从而大大降低了系统的复杂性.
3.2 一致性分析
本文的主要结果总结如下.
实习报告评分标准:“思路清晰,条理清楚,能运用专业理论知识分析具体问题及按要求完成报告”为优秀;“能结合实习情况描述实习内容及解决的具体问题,按要求完成报告”为良好;“罗列材料,缺少分析,基本完成实习报告”为合格;“实习报告与实习内容关系不大或未能按要求完成报告”为不合格。
定理1考虑在网络攻击(2)下的切换多智能体系统(1).如果假设1成立,且攻击权重相等,那么一致性协议(31)以及自适应律(32)保证所有智能体的输出在任意切换下达到渐近一致性.
证 式(33)左右两边积分可以得到

因为图G具有有向生成树,因此矩阵LA具有一个零特征值,其对应特征向量为1N,并且矩阵LA的其它n-1个特征值v2,···,vN位于开的右半平面.令P=[1N v2··· vN]是一个正定矩阵,其各列由矩阵LA的特征向量组成.由此可以得到
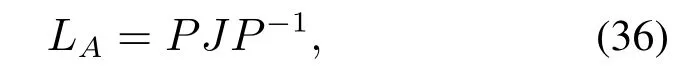
其中J=diag{0,J1}为Jordan标准型,J1是一个正定矩阵.定义ς=P-1η.由式(35)-(36)可计算得

式(43)说明所有智能体的输出渐近达到一致.
注4本文所设计的虚拟和真实协议并没有直接用到非线性动态hi,j,s的信息.利用引理1,只要获得hi,j,s已知上界,设计方法对未知非线性动态依然有效.针对无法获取准确上界情形,可以根据非线性特性,利用鲁棒控制技术、高增益技术、函数逼近技术等处理.
注5切换多智能体系统(1)是标准的切换模型,其中每个智能体的动态在不同子动态之间进行切换.当M={1}时,非线性函数h1,j,s简化为文献[17-19]中的函数.此外,文献[3-4]考虑了切换多智能体系统,但是并没有考虑网络攻击并且需要事先已知控制方向.本文提出的控制方法不仅同时考虑了未知的控制方向及不确定网络攻击,而且解决了多种不确定性之间的耦合问题.
4 仿真例子
为了阐明所设计协议的有效性,本小节给出一个数值仿真,并且以文献[18]中的控制机制作为对比.
考虑一个由5个智能体组成的切换多智能体系统.图1展示了智能体之间的通信图.每个智能体的动态描述如下:
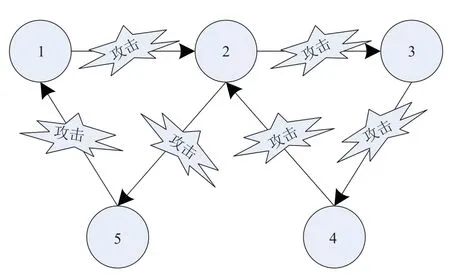
图1 智能体之间通信图Fig.1 Communication graph among agents

其中:j=1,2,3,4,5,σj:[0,∞)→M={1,2},各个智能体中的所有子动态取为

按照第3部分的设计过程,设计如下一致性协议:
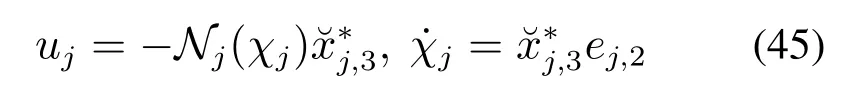
与如下自适应律:

其中所涉及的相关变量和参数如下:
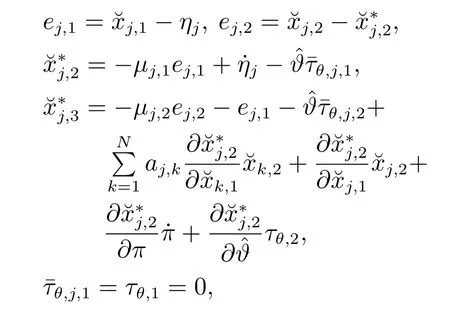
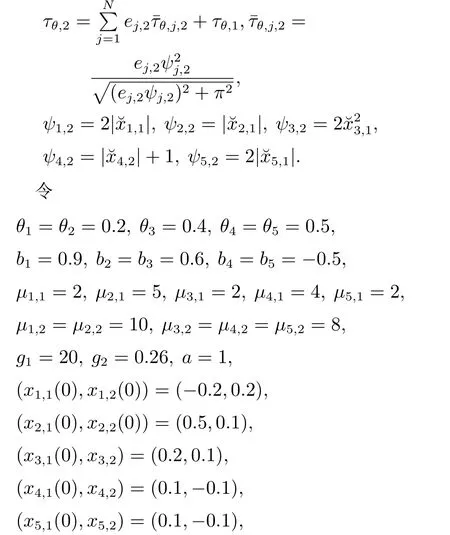
其它初始状态设选为0.攻击参数选为δj=0.5.为了直观呈现一致性,令ey=(y1-y2,y2-y3,y3-y4,y4-y5).本节将与文献[18]中的控制机制做对比.
仿真结果如图2-4所示.如图2为切换信号,每个智能体切换相同.图3分别刻画了在本文提出方法下,文献[18]方法下的一致性误差,以及不考虑网络攻击下的一致性误差.很明显,本文方法下的一致性误差展现出了更好的收敛性,具有更快的收敛时间t=4 s.作为对比,文献[18]方法中的一致性误差则具有更长的收敛时间和更大的幅值,而不考虑网络攻击的方法误差则不收敛.图4为自适应律.文献[17-19]需要构造20个自适应参数消除未知变量影响,本文方法只需要一个自适应参数.结果表明本文提出的控制方法可以更好地解决网络攻击和切换的影响.
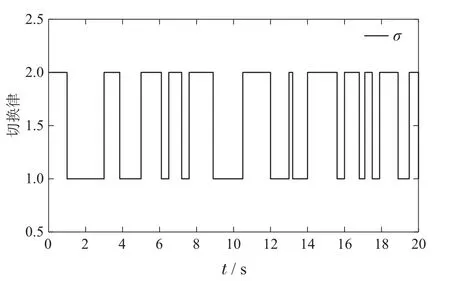
图2 切换律σ的演化Fig.2 The The evolution of switching law σ
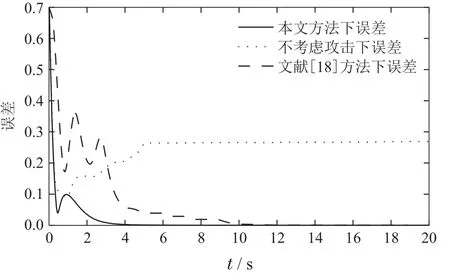
图3 智能体输出误差一致性Fig.3 The consensus error of outputs of the agents
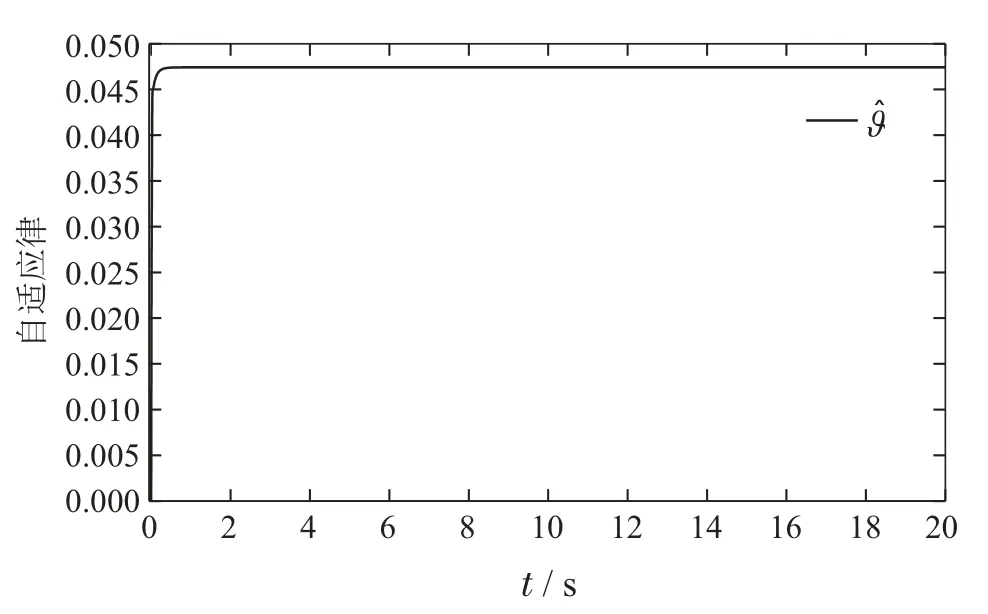
图4 自适应律Fig.4 The adaptive law
5 结论
针对网络攻击的切换多智能体系统,本文建立了自适应安全控制协议.在切换情形,新颖的辅助变量和Nussbaum型函数用于处理网络攻击和未知的控制方向.一个自适应律用于处理系统中的耦合不确定性,极大降低了系统的复杂性.值得进一步研究的问题包括把已设计控制策略拓展到在状态依赖切换网络攻击情况下的多智能体系统,并考虑把所得结果推广到切换拓扑框架下.

