不确定Chua电路系统的固定时间自适应参数估计

石 尚 李 慧 闵惠芳 徐胜元孙永辉

(1.河海大学能源与电气学院,江苏南京 211100;2.南京理工大学自动化学院,江苏南京 210094;3.东南大学自动化学院,江苏南京 234299)

1 引言

作为微分动力系统中十分重要的非线性动力学现象,混沌现象因其在安全通信、激光系统、电子化学、神经生理学等领域的应用,受到学者们的广泛关注[1-5].自混沌学的发展逐渐步入正轨以来,人们一直尝试用肉眼可见的方法去观察混沌这一令人捉摸不透的动力学现象.由此,作为揭开分支与混沌机理过程中的重要研究课题,电学中非线性电路的混沌现象研究逐渐进入人们的眼球.关于非线性电路中混沌现象的研究已有三十年以上的历史,在研究者们的不懈努力下,许多以混沌机理研究为目的的电路被构造出来[6].同时,研究者们还对一部分实用电路中产生的混沌现象进行了密切研究[7].

1983年,加利福尼亚大学的Leon Chua教授设计出了第1个可以通过实验模拟混沌现象的Chua电路[8].这是一个具有里程碑意义的设计,它开辟了混沌行为应用于现实世界的新道路.Chua电路是一个可以产生双涡卷混沌的三阶自治电路,通过赋予一个分段线性负电阻不同形式的参数组合,从而产生尤为丰富的分支与混沌行为.Chua电路是能引起混沌现象出现的自治电路中构造最为简单的一个,任何在三阶自治系统中产生的混沌现象,都可以通过Chua电路系统模拟展现出来.Shilnikov定理中对Chua系统产生的混沌形态做出了严格证明[9].基于此,人们得以通过电路这一形式来对分支和混沌的各种机理进行观察和研究.因此,对于Chua电路的研究引起了很多研究者的兴趣,Chua系统也逐渐成为了混沌现象研究中的标准模型[10-14].

最初的关于Chua电路系统的研究需要假设系统的参数是精确已知的.在实际的电路设计中,由于受到元器件老化、不确定干扰以及测量成本等各种内部外部因素的影响,电路中的某些参数往往很难精确或直接获取.因此,如何解决具有未知参数的Chua电路系统的参数估计问题变得尤为重要,当系统仅有部分状态变量可用时,问题将变得更加困难.为了解决这一问题,学者们提出了各种各样的方法,如:基于延迟嵌入的方法[15-16]、基于控制理论的方法[17-18]等.其中基于控制理论的方法可以通过观测器设计、系统辨识等方法从隐藏变量中估计未知参数,从而得到越来越广泛的应用.文献[19]提出了一种基于最小二乘法的参数估计方法,然而该方法需要假设Chua电路系统的所有状态变量均已知,这在很多情况下无法满足.文献[20]考虑了系统仅有部分状态变量作为输出可测的情况,通过巧妙地引入的坐标变换,将非线性Chua系统转变为可观测的线性系统,并提出了基于标准线性参数辨识的混沌系统参数估计方法.在此基础上,文献[21]提出了基于梯度算法的线性估计方法,通过利用梯度算法不断调整估计器的增益,从而使得估计参数能够收敛到参数的实际值,然而这一算法要求系统的输出及其导数都是已知的.

收敛速度是参数估计过程中非常关键的一个性能指标,前文中所涉及的文献大多仅能实现参数的渐近估计.渐近估计仅能保证参数的估计误差在时间趋向于无穷时趋向于零,因此无法得到更快的估计速度.从时间优化的角度来看,使估计误差有限时间收敛的估计方法才是时间最优的估计算法.此外,有限时间估计算法通常带有分数幂项,使得有限时间参数估计和传统的渐近估计相比,往往具有更好的鲁棒性和抗扰动性.正是由于有限时间参数估计的诸多优点,关于混沌系统有限时间参数估计的研究受到越来越多研究者的关注,并取得了许多积极的成果[22-25].特别地,在最近的文献[26]中,作者针对Chua电路系统提出了一种基于Volterra积分算子的有限时间自适应参数估计算法,和现有结果相比,该算法在实现参数有限时间估计的同时,避免了对输出导数的计算.然而,为了消去未知输出导数的影响,需要针对Volterra积分算子选取几个不同的核函数,这大大提升了算法的复杂度.

注意到,不管是传统的渐近参数估计算法还是近年来被广泛研究的有限时间估计算法,其收敛时间都是依赖于参数的初始估计误差的,并随初始估计误差的增大而增大.为了克服这一缺陷,文献[27]提出了固定时间稳定性的概念.固定时间稳定性在保留了有限时间稳定收敛速度快、收敛精度高等诸多优点的同时,还具有收敛时间不依赖初始值的优良特性,因此成为国内外的研究热点[28-30].近年来,混沌系统的固定时间同步、固定时间控制等问题被大量地研究[31-32],但关于混沌系统的固定时间参数估计问题的研究却鲜有报道.因此,解决混沌系统的固定时间参数估计问题是本文所要考虑的主要问题.

本文针对带有未知参数的Chua电路系统,提出了一种新的基于Volterra积分算子的固定时间自适应参数估计算法,和已有算法相比主要贡献如下:

1) 首先,和已有的基于渐近收敛和有限时间收敛的参数估计策略相比较,本文所提出的固定时间参数估计算法在保证了收敛速度快、收敛精度高的同时,还具有收敛时间不依赖于初始估计误差的特点;

2) 此外,本文所使用的Volterra积分算子,能够有效消除系统初始值的影响,同时避免对系统输出导数的计算,使得所提算法只需用到系统的输出信息,从而能够有效减少传感器的使用,从而有效降低算法的实现成本;

3) 最后,和文献[26]相比,本文所提算法除了能实现固定时间参数估计外,只需要选取一个核函数,从而使得算法复杂度大大降低.

本文剩余部分组织如下:第2节给出了Chua电路系统的建模和预备知识;第3节给出了固定时间自适应参数估计器的设计与稳定性分析;第4节和第5节分别给出了仿真结果和总结.

2 问题描述

2.1 系统建模

如图1所示,Chua电路由3个储能元件(1个电感和2个电容)、1个线性电阻器和1个称为Chua二极管的非线性电阻器组成,其简化非线性模型如下[6]:

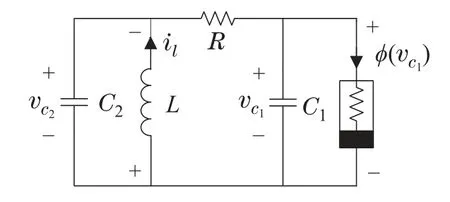
图1 Chua电路系统Fig.1 The Chua system

其中:R是线性电阻,vc1和vc2分别是电容器C1,C2两端的电压,il是通过电感的电流.φ()是关于电容器C1电压的函数,用来表示通过非线性电阻的电流,该非线性函数由如下的奇对称分段线性函数描述:

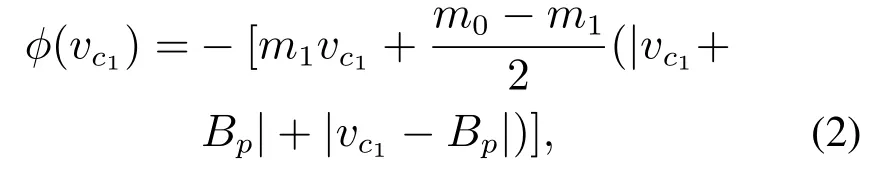
其中m0,m1和Bp为二极管的3个固定常数.根据文献[33],系统(1)可以写成如下的无量纲形式:

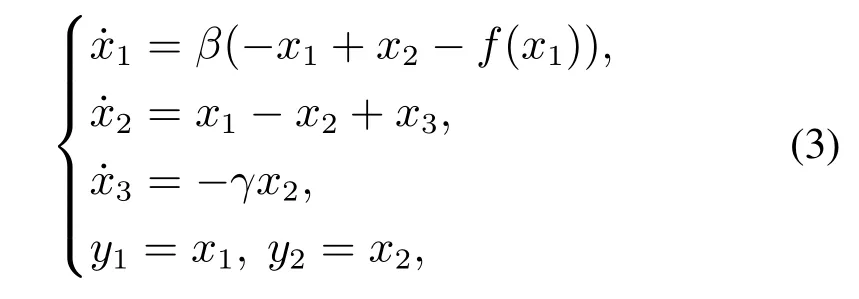
其中y1,y2表示系统的输出,

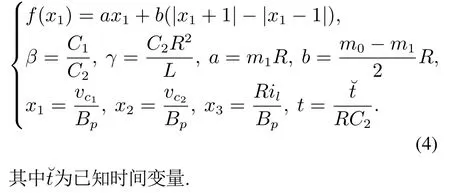
对于系统(3),只需要系统输出y1=x1,y2=x2和t已知,β,a,b和γ均为待估计的未知参数.

由文献[21]可知,当参数选取为γ=27,β=15.6,a=-和b=-附近的固定值时,Chua电路将表现出所谓的双涡卷混沌吸引子.

本文的主要目标为:针对系统(3),考虑当系统仅有y1,y2已知作为输出时,如何在一个不依赖于初始值的固定时间内,实现对参数β,a,b和γ的精确估计.

2.2 固定时间稳定性

考虑如下系统:

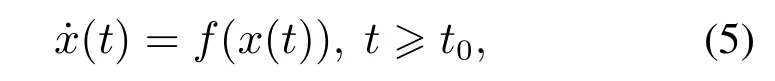
其中:f(0)=0,x(t)∈Rn,f(x(t)):Rn →Rn为一个连续函数,x0=x(t0)表示系统的初始值,t0表示初始时刻为一个定值.

下面将介绍固定时间稳定性的定义和判据.

定义1对系统(5),系统的解记为x(t,x0).如果存在一个不依赖于系统初始值x0的固定时间T,使得对任意初始状态x0,有x(t,x0)=0,∀t≥T+t0成立,那么系统(5)的平衡点x=0是全局固定时间稳定的.

引理1[27]对系统(5),如果存在一个连续正定径向无界的Lyapunov函数V(x(t)):Rn →R≥0,使得

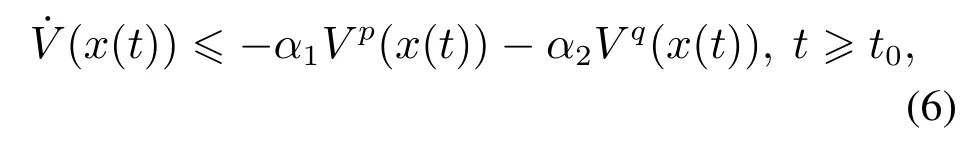
其中:α1＞0,α2＞0,0＜p ＜1,q ＞1,那么系统的原点是全局固定时间稳定的,即对任意初始值x0∈Rn,有x(t,x0)=0,∀t≥Tmax成立,其中Tmax满足

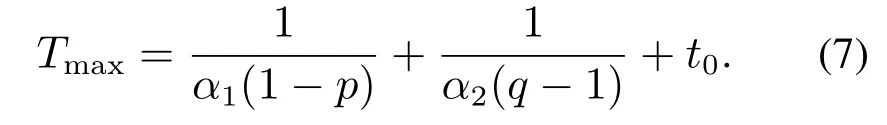
2.3 Volterra积分算子

其中K(·,·):R×R→R希尔伯特-施密特核函数.

用微分方程的形式实现式(8)更方便实际计算,通过对式(8)运用莱布尼茨微分规则,容易证明[VKf](t)可由如下的微分方程来产生:

其中K(i)(·,·)表示K(·,·)关于第2个变量的i阶导数.

3 固定时间参数估计

为了方便参数估计器的设计,我们将系统(3)重新写成如下形式:

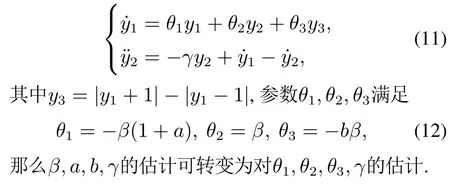
3.1 核函数K(t,τ)的选取

为了计算函数f(t)的Volterra 积分算子的映射[VKf](t),需要先选取核函数K(t,τ).不同于文献[26],本文核函数K(t,τ)选取如下:

注1文献[26]中选取的核函数K(t,τ)满足K(t,τ)=Kh(t,τ)=e-wh(t-τ)(1-e-wτ)N.当利用此核函数估计参数θ1,θ2,θ3,γ时,为了消除未知变量的影响,需要选取具有不同参数wh,w1,w2和相同参数w的核函数Kh,K1,K2.和文献[26]不同,本文只需选取一个核函数就能实现对系统所有未知参数的估计.

3.2 参数估计

对系统(11)两边同时进行积分算子VK运算可得

注2注意到,式(21)中除了参数θ1,θ2,θ3,γ外,其它变量均是已知的,因此可以用来设计参数估计器.然而,直接根据Volterra积分算子的定义式(8)去计算式(21)中的Volterra积分算子映射非常繁琐,用微分方程来产生等式(21)中的所需变量更方便实际计算.

下面的引理中给出等式(21)中的变量[VK(i)yj](t),∀i ∈{0,1,2},∀j ∈{1,2,3}的微分方程产生方式,其证明详见附录.

为了方便估计器的设计,等式(23)可以重新写为

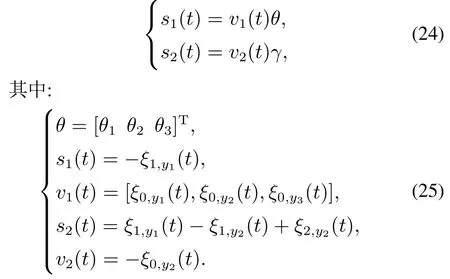
为了设计自适应参数估计器,需要v1(t),v2(t)满足如下的持续可激励假设:

假设1函数v1(t),v2(t)满足持续可激励条件,即存在常数r ＞0,T0＞0使得如下不等式对∀t≥T0成立:

注3由文献[35-36]可知,假设1中的持续可激励条件是解决自适应参数辨识问题的必备条件.在这一假设条件下,通过直接应用文献[35-36]中的理论方法,容易针对系统(24)设计自适应参数估计算法,实现参数的渐近估计.然而,本文的主要目标是实现参数的固定时间精确估计,因此传统的渐近估计算在此无法满足要求.

可以发现式(24)中两个等式一个是向量形式一个是标量形式,因此对两式分别左乘(t)和v2(t)可得

定义如下辅助变量:

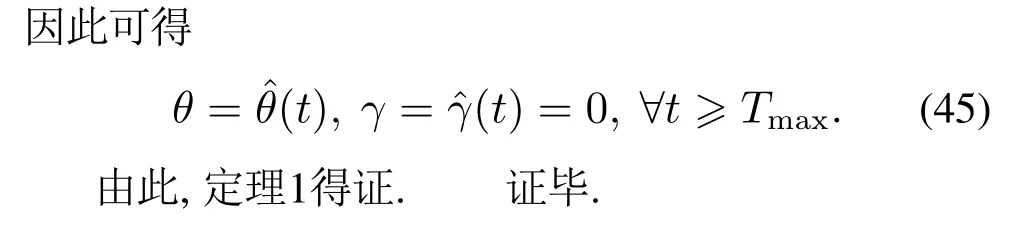
4 仿真算例

为了验证算法的有效性,本节将对系统(3)运用定理1中提出的固定时间参数估计算法进行仿真验证,并通过与文献[26]所提出的有限时间参数估计算法进行比较,以验证所提算法的优越性.

4.1 参数选取

对系统选取如下的初始状态和参数:

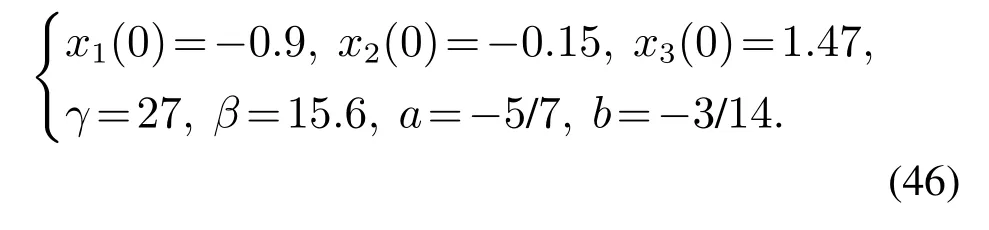
系统的混沌吸引子及其在各坐标平面的投影如图2所示.

图2 系统的混沌吸引子图Fig.2 Chaotic attractor of system

按照定理1设计固定时间自适应参数估计算法,其参数选取如表1所示.按照文献[26]设计有限时间参数估计算法,其参数选取与文献[26]相同.为了验证算法的固定时间收敛性,分别选取如下两个不同的自适应初始值:

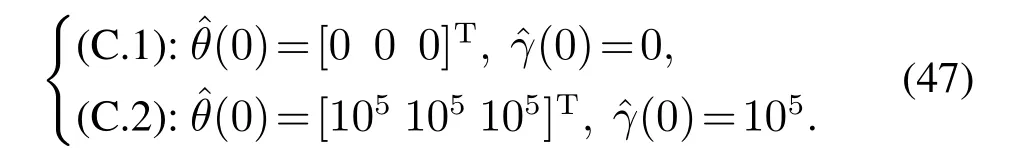
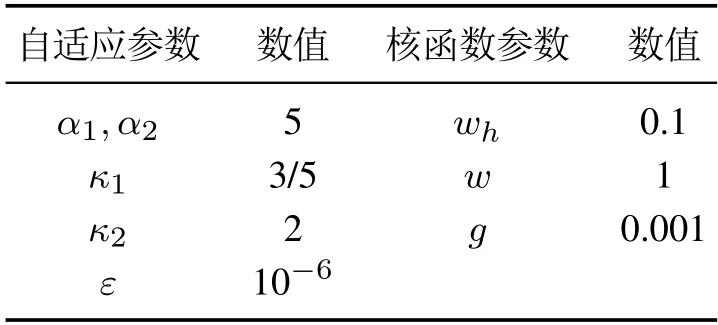
表1 估计器参数选取Table 1 Parameter selection of the estimator

下面将分别针对以上两个不同的自适应初始值,分别对本文所提出的固定时间参数估计算法和文献[26]所提出的有限时间参数估计算法进行仿真验证和比较.

4.2 仿真结果分析

当选取r=10-12,T0=0.6 s,可以验证假设1成立.由定理1可得Tmax的表达式

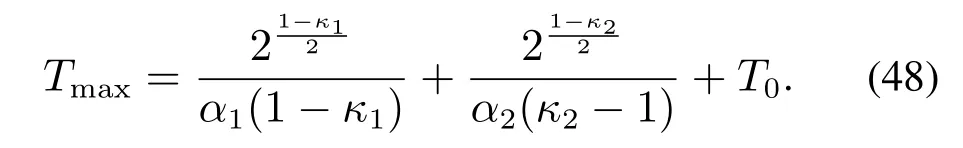
将表1中的参数代入上式可以算出参数估计器的收敛时间Tc＜Tmax=1.4 s.固定时间自适应参数估计算法的仿真结果见图3和图4.选取自适应初始值(0)=[0 0 0]T,(0)=0,仿真结果见图3.由图3可得,本文所提出的算法能够在1.4 s内实现对系统参数β,γ,a,b的准确估计.当选取一个大的自适应初始值=[105105105]T,(0)=105,仿真结果见图4.由图4可得,即使在大的初始状态下,所提算法依然能够在1.4 s内实现对系统参数β,γ,a,b的准确估计,由此验证了本文所提算法的固定时间收敛性质,即收敛时间Tc有一个不依赖初始值上界Tmax.

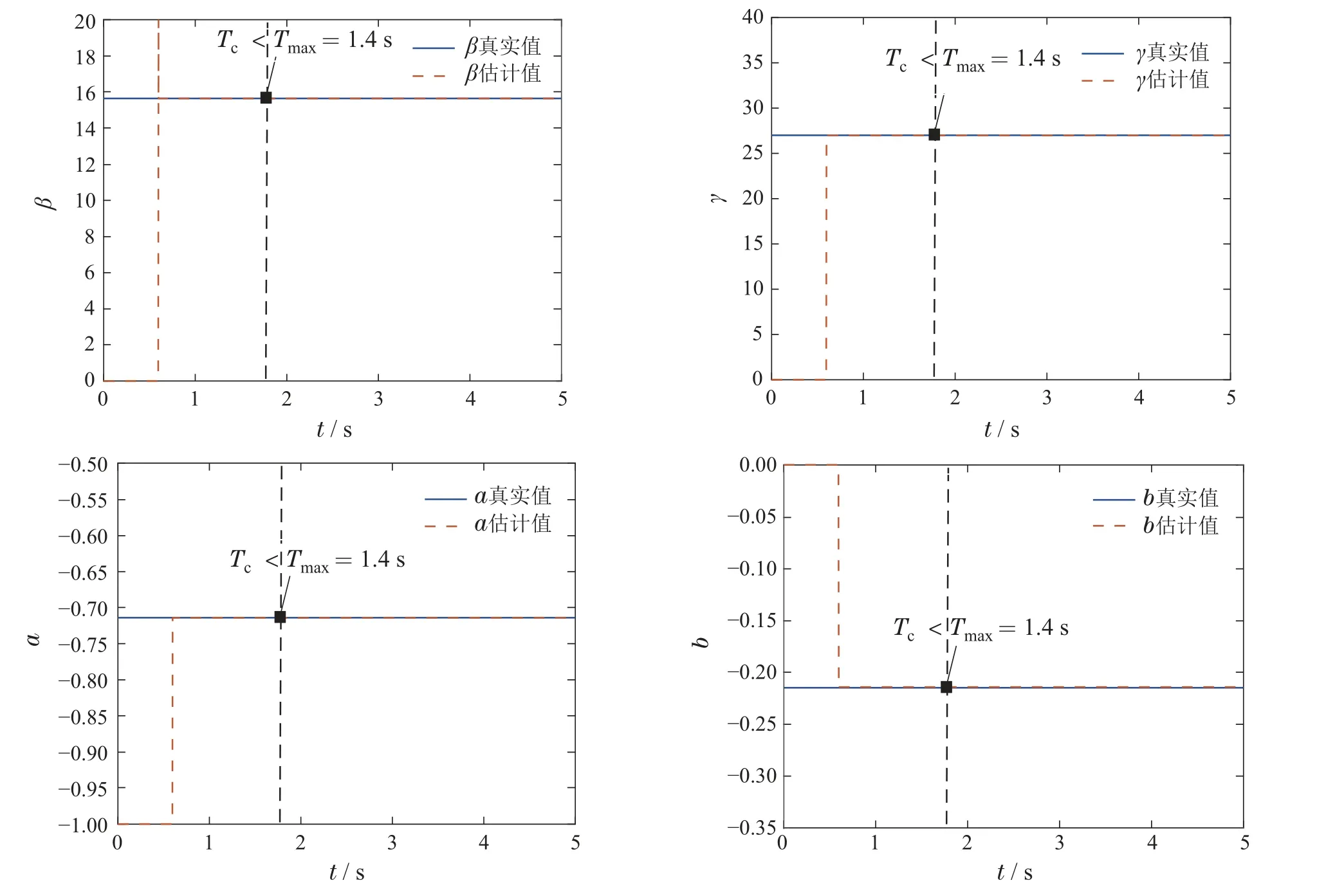
图3 自适应初始值(0)=[0 0 0]T,(0)=0下的固定时间参数估计Fig.3 Parameter estimation under adaptive initial values (0)=[0 0 0]T,(0)=0

图4 自适应初始值(0)=[105 105 105]T,(0)=105下的固定时间参数估计Fig.4 Parameter estimation under adaptive initial values (0)=[105 105 105]T,(0)=105

文献[26]所提出的有限时间自适应参数估计算法的仿真结果见图5.由图5可知,选取自适应初始值(0)=[0 0 0]T,(0)=0时,有限时间参数估计算法也能在一个很短的时间Tc=5 s 内实现对参数的有限时间估计.然而,当选取一个大的自适应初始值(0)=[105105105]T,(0)=105时,可以发现参数估计器的收敛时间增加到Tc＞150 s.由此也说明了本文所提出的固定时间参数估计算法的优越性.

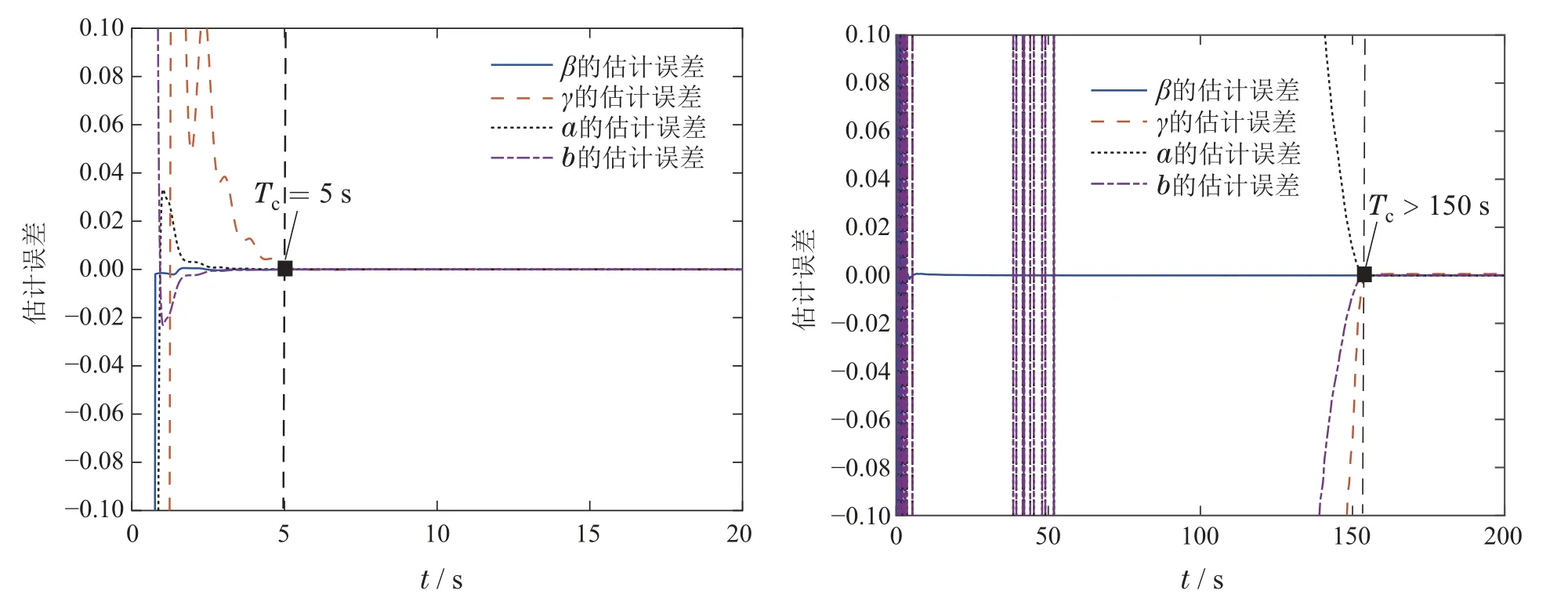
图5 有限时间参数估计:左图:初始值(0)=[0 0 0]T,(0)=0;右图初始值(0)=[105 105 105]T,(0)=105Fig.5 Finite-time parameter estimation:Left:initial values (0)=[0 0 0]T,(0)=0;Right:initial values(0)=[105 105 105]T,(0)=105

附录:引理3证明

由Volterra积分算子的定义式(8)和式(17)可得

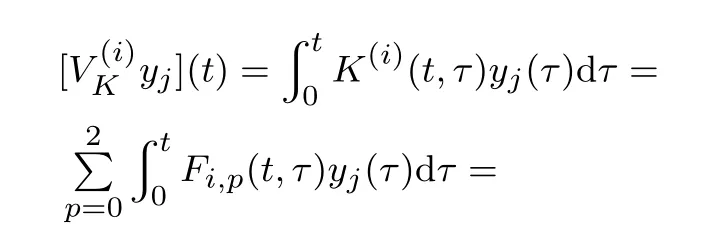
5 总结

本文针对不确定Chua电路系统,提出了一种新的自适应固定时间参数估计算法.与传统的渐近估计和有限时间估计算法相比,本方法在实现对参数精确估计的同时,还具有收敛时间不依赖于初始估计误差的优良特性.需要指出的是,和许多已有文献类似[21,26],尽管本文所使用的持续可激励假设已经在实验中被验证,但缺乏严格的理论证明.并且本文所提算法仅能实现对参数的估计,不能实现对未知状态的估计.此外,由于混沌系统对初始值的选取非常敏感,对系统初始状态的估计也具有重要的理论和实际意义.因此,如何解决以上问题是笔者今后要考虑的主要课题.