基于TS-FNN的城市固废焚烧过程MIMO被控对象建模

丁海旭,汤 健,夏 恒,乔俊飞

(1.北京工业大学信息学部,北京 100124;2.智慧环保北京实验室,北京 100124)

1 引言

城市固废焚烧(municipal solid wastes incineration,MSWI)技术具有无害化、减量化、资源化等突出优势,已成为目前世界范围内处理城市固废(municipal solid wastes,MSW)的主要技术手段之一[1-2].截至2020年,我国使用机械炉排炉的固废焚烧发电厂占比已超过86%[3].MSWI过程具有强非线性、强耦合、大时变、不确定性等诸多特征[4-5],建立精准的被控对象模型是实施智能控制技术的基础与必要准备.因此,针对MSWI过程进行被控对象模型设计的研究具有重要意义.

传统的被控对象模型通常是基于机理分析构建的.机理模型通常是依据于物料平衡方程、能量平衡方程、化学动力学等原理建立的数学模型.文献[6]针对并罐式无钟布料设备建立了从流量控制闸门到坯料表面的综合数学模型,改善了并联料斗式高炉负荷分布不均的问题.文献[7]针对高炉中竖井角度和炉料消耗不均匀的问题,在几何轮廓模型和势流模型上进行改进,提高了机理模型的精度.文献[8]基于离子液体体系的传递机理开发了一种用于实际溶剂的筛查模型,其为被研究系统提供了温度效应预测.虽然机理模型具有直观反映系统内在规律与结构联系的能力,然而,MSWI 过程在本质上具有复杂多变和不确定的特性[9].近年来,随着人工智能的兴起,基于数据驱动的机器学习方法为MSWI过程的被控对象建模提供了解决思路.

数据驱动模型是通过挖掘系统输入输出数据间的映射关系构建的.人工神经网络(artificial neural network,ANN)因其良好的学习能力和非线性逼近能力而广泛地应用于复杂工业系统的过程分析[10-12].文献[13]采用动态递归神经网络构建多输入被控对象模型,在识别具有连续生产性质的工业被控对象中具有良好的应用前景.文献[14]针对锅炉燃烧发电中煤质与负荷波动频繁难以建模的问题,将锅炉模型的输入按照实际物理规律进行优化组合,设计了一种基于非对称神经网络的被控对象模型.综上所述,ANN在工业过程的被控对象建模中已成为目前的研究热点.

MSWI过程内部机理反应复杂,多个操作量与被控量耦合严重,系统规则难以挖掘,具有典型的模糊特性.针对MSWI这类复杂工业过程,模糊神经网络(fuzzy neural network,FNN) 提供了良好的解决方案[15-16].FNN 作为一种模糊的自适应方案,其兼具模糊系统的非线性处理与分析能力,又具有ANN的参数学习与动态优化能力,近年来已被广为研究[17-18].当前大多数FNN的设计都是多输入单输出(multi-input single-output,MISO)模型,其具有建模精度高、参数优化快的优势.文献[19]针对系统建模和噪声消除问题,提出了一种自演化补偿的区间二型FNN,通过多个基准非线性实验证明了模型的有效性.文献[20]设计了一种基于合作策略的FNN,提出了一种与参数优化配合的综合评估算法(comprehensive evaluation algorithm,CEA)以增强网络泛化性能,通过污水处理中的氨氮预测实验验证了模型的精度.文献[21]将T-S(Takagi-Sugeno)型FNN与遗传算法相结合,并利用此模型实现了对丙烯酸苄酯合成工艺条件及关键指标的准确预测与有效优化.然而,MSWI过程是一个典型的多输入多输出(multiple-input multiple-output,MIMO)的工业过程,构建其被控对象模型要求FNN不但要具有良好的非线性逼近能力,还要具有同步输出多个参数的能力.

在现有研究中,一些学者采用构建多个单输出网络模型的方法以满足复杂系统的多输出需求.文献[22]设计了一种多RBF神经网络板形识别模型,用多个子网络分别识别不同的特征参数,识别模型能够正确识别出全部板形缺陷的类型.文献[23]使用深度特征聚类(deep feature clustering,DFC)组合了多个神经网络的特征,该方法在较短的处理时间内提高了情感识别的性能.然而,对于强耦合的复杂系统而言,构建多个单输出网络的建模方法割裂了系统多变量之间的关系且难以保证输出间的同步性.

最近的研究表明,模型对同一系统中多个任务同时学习可以彼此助益,即利用多个学习任务中所包含的有用信息可帮助其提升获取更精确的模型参数.文献[24]针对火力发电厂因非线性强、多变量耦合等原因导致难以建立精确数学模型的问题,采用MIMO神经网络进行建模,取得了良好的效果.文献[25]针对污水处理运行过程的重要指标出水总磷和出水氨氮难以实时测量的问题,设计了一种基于FNN的多参数软测量方法.根据以上分析,本文对T-S型FNN的结构进行了如下改进:构建共享隶属函数层与共享规则层,使用多输出误差对隶属函数的中心、宽度进行多角度校正,使得同一对象中的多任务学习具有协调兼顾的能力;构建多个后件子网络,使其分别针对不同输出任务进行校正,对多输出任务进行精准拟合,并保证其同步输出.

综上所述,本文针对MSWI过程的工艺特点,构建了一种基于MIMO 的Takagi-Sugeno 型FNN(MIMO Takagi-Sugeno FNN,MIMO-TSFNN)被控对象模型.首先,设计了专家评判机制用于运行工况识别,通过异常数据剔除与数据归一化进行预处理;然后,结合布风布料过程机理分析,通过计算皮尔逊相关系数(pearson correlation coefficient,PCC)提取能够反应系统状态的关键操作量与被控量;最后,构建MIMOTSFNN多任务学习模型,采用梯度下降算法对网络参数进行优化,同步调整网络共享神经元参数,针对多输出任务对后件子网络的模糊系统参数能够进行校正.通过北京市某MSWI电厂的过程数据验证了被控对象模型的有效性.

2 面向被控对象建模的MSWI特性分析

2.1 MSWI工艺流程

基于炉排炉的MSWI工艺流程包括:固废储运系统、固废焚烧系统、余热锅炉系统、蒸汽发电系统、烟气处理系统与烟气排放系统.固废进入焚烧炉,在炉体的高温热辐射和加温后的助燃风作用下,经过干燥、燃烧、燃烬过程,固废在高温作用下转化成为气体无机物并释放热量.如图1所示.

图1 MSWI的工艺流程Fig.1 MSWI process flow

2.2 模型影响因素分析

研究MSWI的控制过程是分析模型影响因素的基础,其主要操作对象为一次风机及其风门挡板、二次风机、干燥炉排、燃烧炉排、燃烬炉排等设备;主要被控变量为烟气含氧量、炉膛温度、主蒸汽流量等.MSWI过程的控制过程如图2所示.

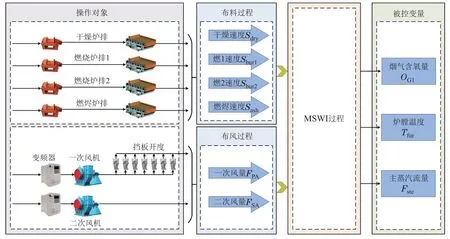
图2 MSWI的控制过程Fig.2 MSWI control process

根据MSWI的工艺特点,可将其归纳以一个典型的“布风布料”过程,关键操作变量包括:各段炉排空气流量、一次风总流量、二次风流量、各段炉排速度.根据MSWI控制需求,采集的关键被控变量包括:主蒸汽流量、炉膛温度和烟气含氧量.本节采用皮尔逊相关系数PCC对操作变量与被控变量之间的相关性评估如下.

其中:xi和yi分别为两组变量所对应的数据序列,N为样本个数.

根据PCC的定义:当ρXY为正数时,变量之间为正相关,反之为负相关,ρXY的绝对值越大相关性越强,当计算结果为非数值(not a number,NAN)时,则说明某一变量未发生变化.计算结果如图3-8所示.

图3 布风操作变量与主蒸汽流量的PCC值Fig.3 PCC value of air distribution operating variable and main steam flow

图4 布风操作变量与炉膛温度的PCC值Fig.4 PCC value of air distribution operating variable and furnace temperature

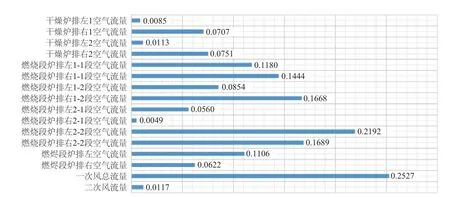
图5 布风操作变量与烟气含氧量的PCC值Fig.5 PCC value of air distribution operating variable and flue gas oxygen content

图6 布料操作变量与主蒸汽流量的PCC值Fig.6 PCC value of material distribution operating variable and main steam flow

图7 布料操作变量与炉膛温度的PCC值Fig.7 PCC value of material distribution operating variable and furnace temperature

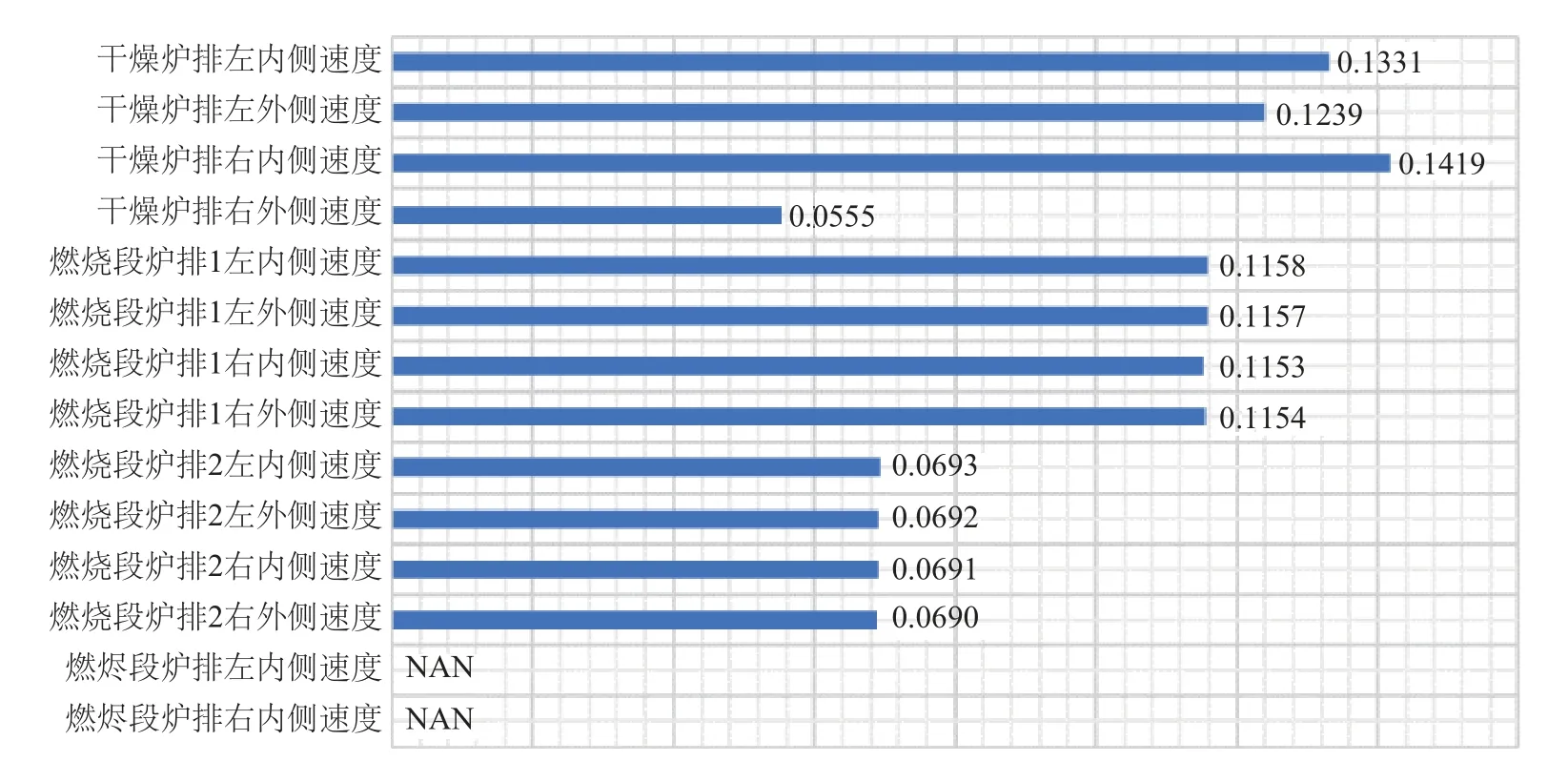
图8 布料操作变量与烟气含氧量的PCC值Fig.8 PCC value of material distribution operating variable and flue gas oxygen content

由图3-4可知,部分一次风各段流量PCC值较高且正负相关均存在,而一次风总流量却与主蒸汽流量、炉膛温度的PCC值极低,这表明各子管之间存在着强耦合性,并不能选取局部某一根子管作为主要变量.此外,由图3-4可知,二次风流量与主蒸汽流量、炉膛温度的PCC值是最高的,因此可选取二次风作为操作变量.由图5可知,一次风各段流量与烟气含氧量均呈现正相关,且一次风总流量与烟气含氧量的PCC值最高,因此选取一次风总流量作为关键操作变量.由图6-8可知,干燥炉排与主蒸汽流量、炉膛温度、烟气含氧量的PCC值均为最高.此外,各段炉排之间的机械结构是相互独立的,并不存在耦合,因此,选取干燥炉排平均速度作为关键操作变量.

3 MSWI过程被控对象模型

3.1 建模策略

针对MSWI过程工艺特点,本文提出的MSWI过程MIMO被控对象建模策略如图9所示.

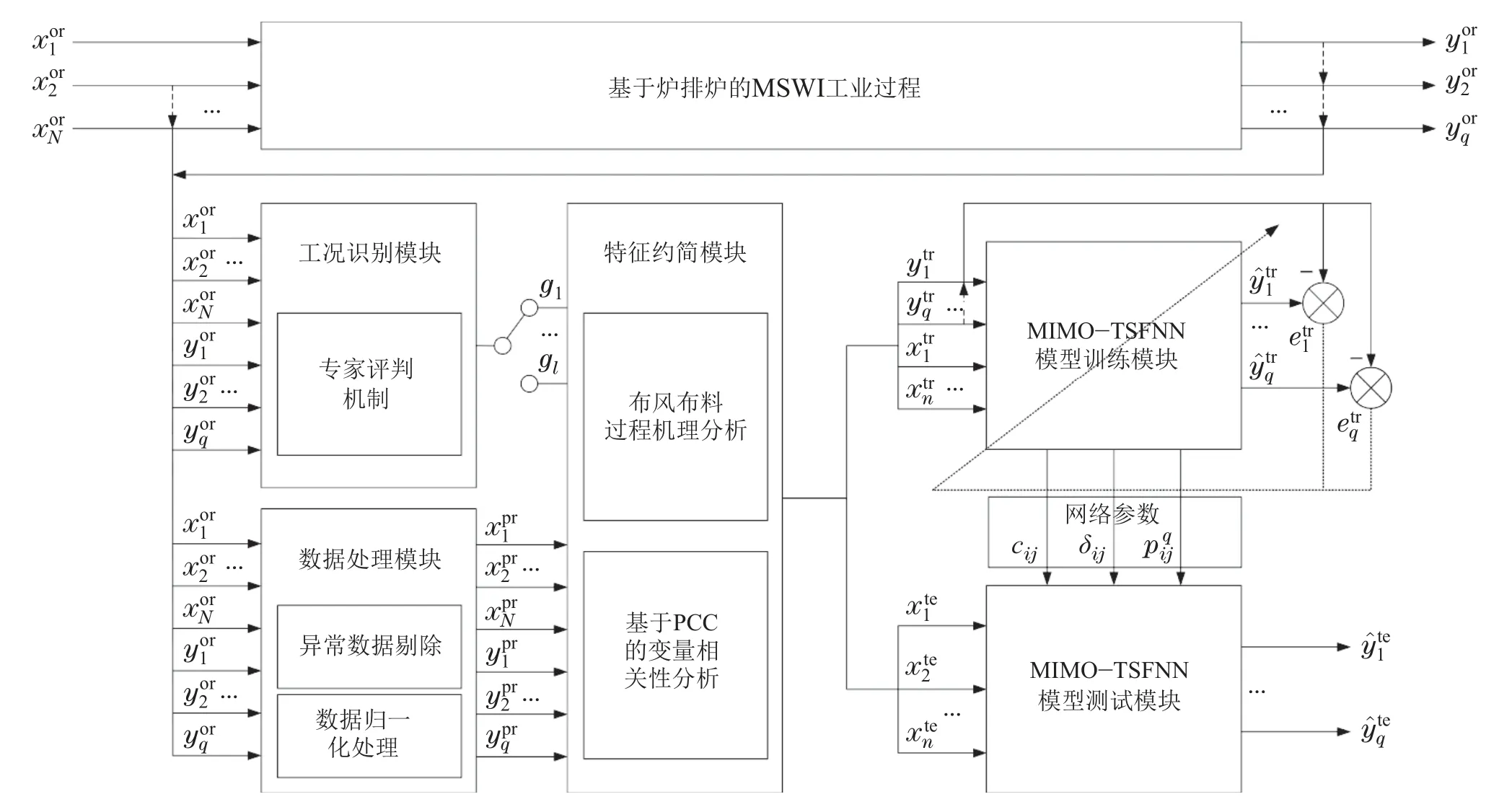
图9 基于数据驱动的MSWI过程MIMO被控对象建模策略Fig.9 Modeling strategy of MIMO controlled object based on data drive in MSWI process

3.2 建模算法及算法实现

3.2.1 工况识别模块

MSWI过程受MSW分类程度、经济水平、气候季节等因素影响,具有多工况特性,通常需要依靠专家经验对不同工况进行判别.现场领域专家依据先验知识判断当前工况.在此基础上,本模块建立了一种工况识别专家评判机制.

3.2.2 数据预处理模块

1) 异常数据剔除.

MSWI过程检测环境恶劣、设备损耗大,如未及时排除仪器故障等因素,会造成检测数据失真.通过绘制分位数图对数据的正态分布性进行检测并采用3σ准则[26]对异常数据进行剔除.设定样本数据的维度为q×K,q为MSWI过程的被控变量数量,K为样本的总数量,样本数据用φsk,s=1,2,···,q,k=1,2,···,K表示,其中为样本均值,其标准偏差为

2) 数据归一化处理.

MSWI过程高度复杂,测得的变量较多且量纲不同.为了保证数据指标之间的统一性,对其执行归一化操作如下:

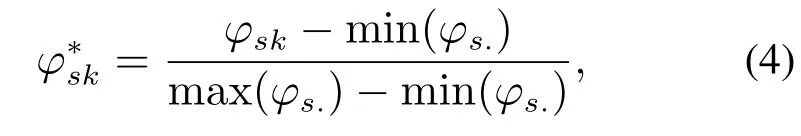
其中φs.为变量s的样本向量.

3.2.3 特征约简模块

研究MSWI被控对象模型的关键是选择合适的操作量与被控量,MSWI过程的操作量与被控量多达几十个,且部分变量之间具有高度耦合性.针对我国MSWI国情,需要在实际运行情况进行特征约简,从而用于构建被控对象模型.因此,本模块建立了一种基于过程数据分析的特征约简机制,通过计算变量之间PCC值对MSWI过程中的变量进行选取与融合.

3.2.4 MIMO–TSFNN模型训练模块

1) 模型结构设计.

针对MSWI 过程设计了如图10 所示的MIMOTSFNN模型结构,对其数学描述如下.

图10 MIMO-TSFNN模型Fig.10 MIMO-TSFNN model

输入层:该层设有n个神经元,其作用是将输入值进行传递,当第k个样本进入时,其输出可表示为

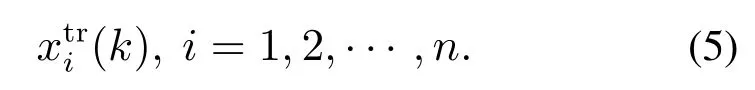
隶属函数层:该层设有n×m个神经元,每个节点代表对应输入量的隶属度值,隶属函数可表示为

式中cij(k)和δij(k)是隶属函数的中心和宽度,j=1,2,···,m.

规则层:该层设有m个神经元,采用模糊连乘算子作为模糊逻辑规则,规则层第j个神经元输出为

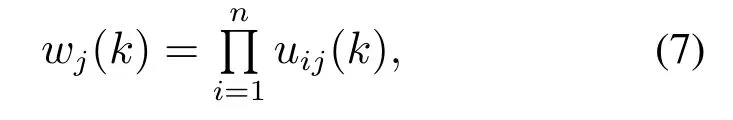
对规则层输出进行去模糊化以获得输出权重为

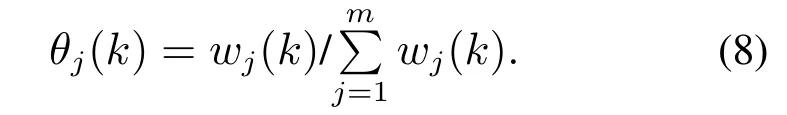
后件层:该层共有m×q个神经元,每个节点执行T-S型模糊规则的线性求和,该层的作用是计算每条规则所对应输出的后件参数,后件参数由后件网络计算得出,将其表示为

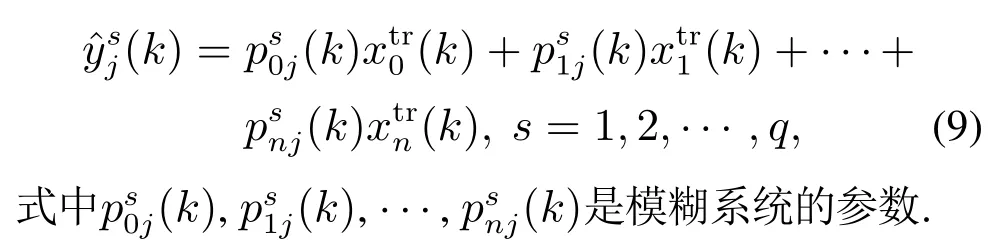
输出层:该层设有q个输出节点,每个节点对输入参数执行加权求和,得到输出层输出为

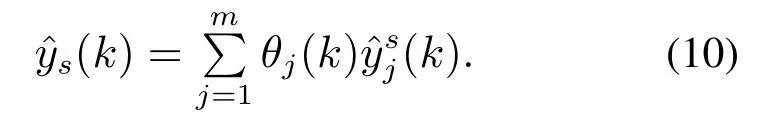
2) 模型参数学习.

通过梯度下降法对模型参数进行迭代求解[27],相关算法定义如下.

3) 模型评价指标.

采用均方根误差(root mean squared error,RMSE)与平均百分比误差(average percentage error,APE)评估建模效果,相关定义如下:

式中:k为当前输入样本,K为样本总数.

3.2.5 MIMO–TSFNN模型测试模块

MIMO-TSFNN模型在训练完成后,需要通过测试以证明模型的有效性.测试集输入变量记为:模型计算输出变量记为:计算测试数据集的RMSE与APE,当模型测试模块达到期望的拟合效果与建模误差后,则表明MSWI过程的被控对象模型建模有效.

4 实验验证

4.1 实验描述

本实验对北京市某MSWI发电厂的进行数据采集,采样频率为1 s/次.本节分别针对数据预处理、特征约简、被控对象模型训练与测试进行相应实验,结果如下.

4.2 实验结果

4.2.1 数据预处理实验

通过绘制样本数据的分位图以验证数据集是否满足正态分布的特性.原始数据中关键被控量的分位数如图11所示.

图11 关键被控量分位数图Fig.11 Quantile chart of key controlled quantities

由图11可知,提取的MSWI过程数据较好地分布于直线附近,验证了其正态分布的特性.在此基础上,使用3σ准则对异常数据进行剔除并对全部数据进行归一化处理,得到预处理后的变量为

4.2.2 特征约简实验

选择1×105时刻的炉排速度值,绘制图像如图12所示.

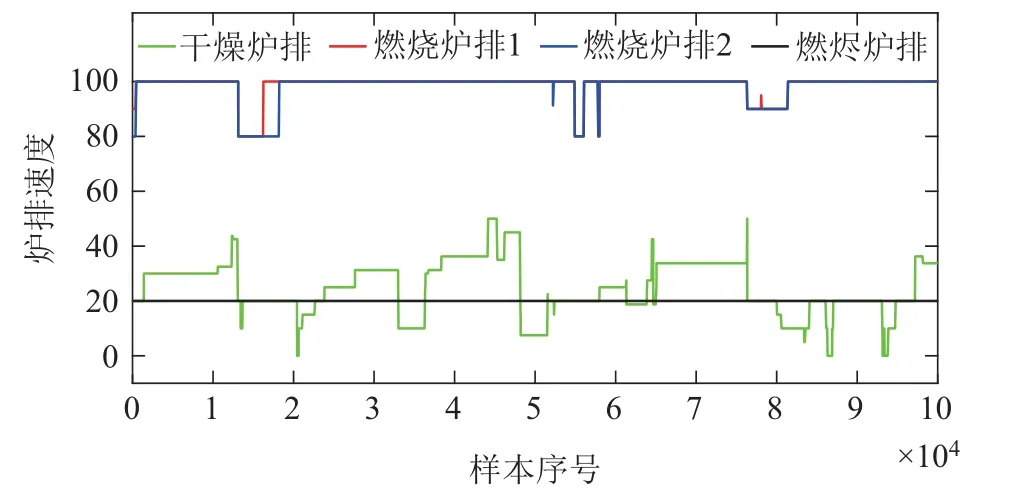
图12 MSWI过程的炉排速度变化Fig.12 Grate speed change in MSWI process

布料过程中,干燥炉排对MSW的脱水作用至关重要,对干燥炉排的速度调节是目前MSWI行业内公认的结论,结合图12可知,对干燥炉排的调节最为频繁,其与被控变量的关系最为紧密,而燃烧炉排1、燃烧炉排2的调速并不多,且其几乎是联动进行变化的,燃烬炉排全程均未发生变化.计算模型操作/被控变量之间PCC值如表1所示.

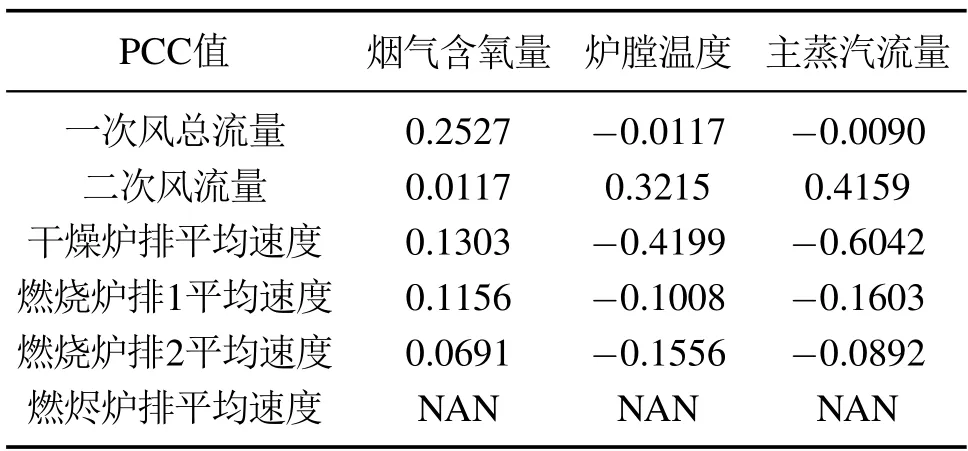
表1 操作/被控变量间PCC值Table 1 PCC value of manipulation variables and controlled variables

根据表1的结果,选取的关键操作变量为一次风总流量、二次风流量和干燥炉排平均速度,关键被控变量为烟气含氧量、炉膛温度和主蒸汽流量.

4.2.3 MIMO–TSFNN模型训练实验

MIMO-TSFNN模型训练实验在工况识别、数据预处理和特征约简实验的基础上,将得到的1×105组数据中的8×104组作为训练样本.模型的参数设置为:输入层神经元为3个,隶属度函数层神经元个数为3×12 个,规则层神经元个数为12个,后件层神经元个数为12×3个,输出层神经元为3个,训练迭代步数为500次.被控对象模型训练过程中的RMSE与参数学习的变化曲线如图13所示;参数学习的变化曲线如图14所示,其中每个子图代表神经元的隶属函数中心cij、宽度δij和模糊系统参数在迭代过程中的变化;模型的训练过程中的拟合效果如图15所示.

图13 模型训练过程RMSE变化Fig.13 RMSE changes during model training

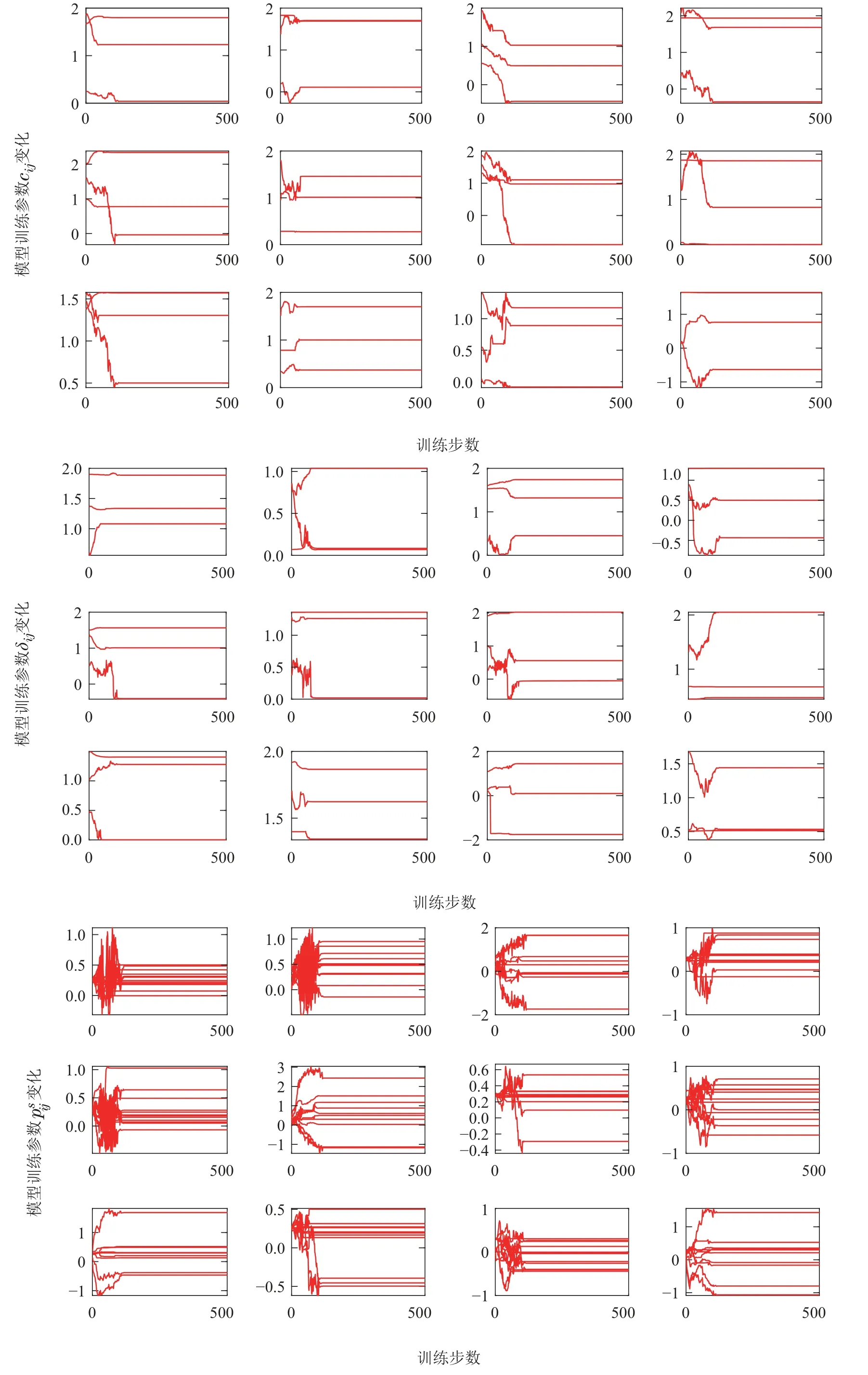
图14 模型训练过程参数变化Fig.14 Parameters changes during model training

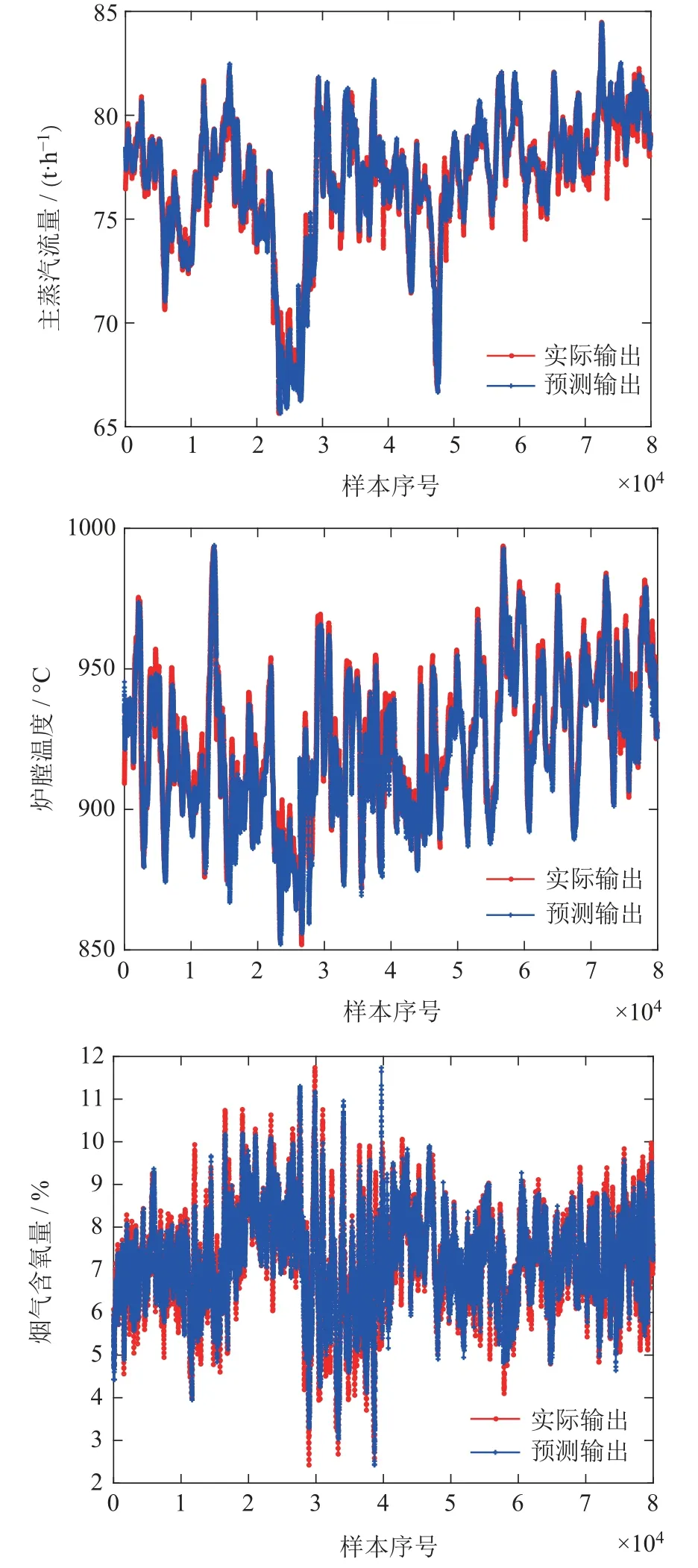
图15 训练样本拟合效果Fig.15 Training sample fitting effect

由图13-15可知,本文所提出的MIMO-TSFNN模型在训练过程中收敛速度快,能够快速达到期望误差,模型的建模精度较高.

4.2.4 MIMO–TSFNN模型测试实验

将1×105组数据中的2×104组作为测试样本,模型的测试拟合效果如图16所示.

由图16可知,模型在多输出样本中均体现出了良好的逼近能力,兼顾了多样本输出的学习任务,具有良好的泛化能力.

图16 测试样本拟合效果Fig.16 Testing sample fitting effect

4.3 方法比较

为了验证该模型的有效性,本节选取基准前馈神经网络TSFNN、RBFNN和反向传播神经网络(back propagation neural network,BPNN)进行对比实验,其中:TSFNN、RBFNN和BPNN的隐含层神经元设置为12,网络训练的迭代步数设置为500次.使用RMSE 与APE作为性能评价指标,对计算结果进行反归一化以使针对不同量纲的评价指标更清晰,被控对象模型的建模效果评价如表2所示.

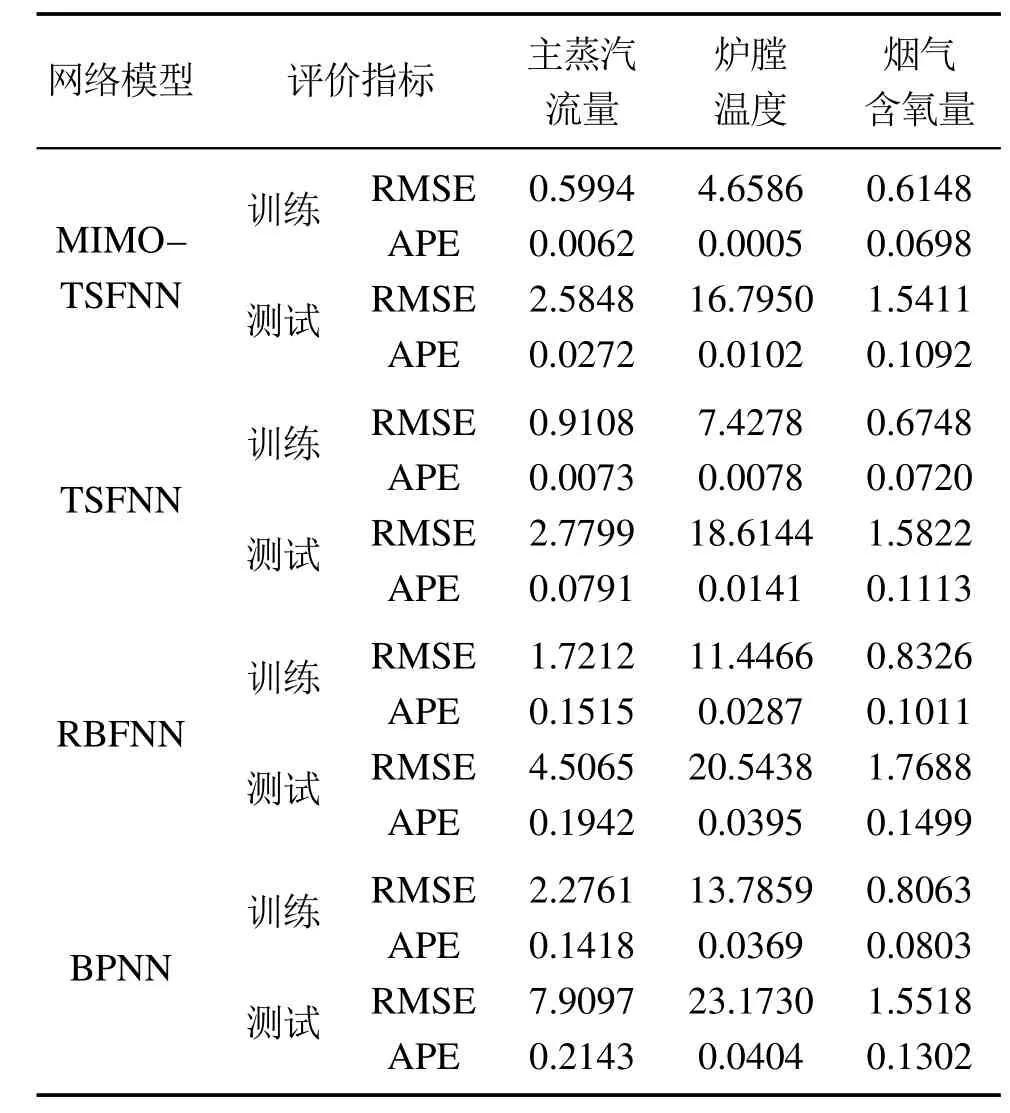
表2 被控对象模型的建模效果评价Table 2 Evaluation of modeling effect of controlled object model

根据表2进行分析可知:

1) MIMO-TSFNN模型在实验中体现了良好的泛化能力,训练与测试的RMSE和APE均达到了理想的精度.与同类基准网络相比,本文提出的MIMOTSFNN 模型具有良好的预测精度,达到了最小训练RMSE(0.5994,4.6586,0.6148),APE(0.0062,0.0005,0.0698)和最小的测试RMSE(2.5848,16.7950,1.5411),APE(0.0272,0.0102,0.1092).这是因为MIMO模型针对同一工业过程的对象的多任务学习具有协调兼顾的能力,模型对多个任务的学习可以彼此助益且多个输出任务之间具有互补性与容错性.MIMO-TSFNN能够利用多个学习任务中所包含的有用信息帮助每个任务学习,从而得到更为准确的回归模型.

2) 结合图13中模型训练过程的RMSE变化可知,不同网络均实现了对MSWI被控对象的建模.此外,模型对不同回归任务的收敛速度也体现出差异性,RBFNN与BPNN的收敛速度相对较慢,学习能力也相对较弱,而MIMO-FNN在收敛速度上具有明显的优势且学习能力较强,这是因为其兼具模糊系统的非线性处理与分析能力,且其利用了多任务之间的多个损失函数,提高了网络的学习能力,具有更强的动态优化能力.

3) 结合图14可知,网络共享的隶属函数层神经元具有同步调整中心、宽度的能力,后件子网络的模糊系统参数能够针对不同输出任务进行校正,各参数学习速度较快.分析图15-16可知,模型能够同步输出多个参数,网络训练及测试的拟合效果好,对强非线性实际工业数据具有较强的逼近能力.

5 结论

MSWI过程具有多对象、多参量、强耦合和大时变等特征,是一个高度复杂的强非线性过程,构建该过程的被控对象模型是研究其优化控制的基础.针对这一问题,本文建立数据驱动MIMO-TSFNN的被控对象模型,其具有如下贡献:解决了MSWI过程内部机理难以分析,多变量耦合性强、内部规则难以挖掘的问题,为研究该过程的优化控制奠定了模型基础;针对工艺特点,设计了具有多工况识别与特征约简的建模策略,模型具有较好的鲁棒性与适用性;建立的MIMO-TSFNN模型具有多输出学习能力,利用多任务之间的互补信息同时对多个被控量进行精准拟合,并对网络参数进行在线更新.综上所述,本文提出的基于MIMO-TSFNN的MSWI过程被控对象建模方法具有多任务学习能力,建模精度较高,针对炉排炉被控对象建模具有一定的应用价值.