基于多质点模型的动车组精准停车自适应控制

李茂青 ,王以庆 ,高云波 ,阳长琼

(1.兰州交通大学自动化与电气工程学院,甘肃兰州 730070;2.兰州交通大学光电技术与智能控制教育部重点实验室,甘肃兰州 730070)

1 引言

列车自动驾驶系统(automatic train operation,ATO)作为列车自动控制系统的一个重要的子系统,实现对列车的牵引和制动控制,它使得列车处于最佳运行状态,保证列车舒适、准点、节能、高效的运行.精准停车作为该系统的一个重要的性能指标,列车进站停车位置不准确不仅会直接影响到列车的准点运行,还有可能影响列车与地面的通信[1].对于建有屏蔽门的车站,其精度通常要求列车门正中心和屏蔽门正中心的停车误差在±30 cm之内,这要求ATO在停车前快速精确地调整速度.在动车组实际运行过程中,各节车厢乘客人数不仅有所差异,且是随机和未知的,动车组运行环境不同,使得动车组模型包含未知性,进而影响动车组的停车精度.因此,研究动车组建模与控制方法对保障动车组安全、高效运行具有重要意义.

列车动力学模型是精准停车的重要依据,目前,列车牵引计算模型可分为单质点和多质点模型两类[2].文献[3]围绕列车单质点模型进行研究,通过分析列车模型的制动特点,从面向控制的角度设计列车制动模型,将列车制动过程用一阶动态系统近似描述,并取得较为满意的效果,但该模型无法补偿坡道和弯道引起的附加阻力.在此模型的基础上,文献[4]针对列车在实际运行过程中,制动模型参数未知和参数变化的情况,设计自适应控制器,使列车达到既定停车要求.文献[5]在文献[4]的基础上,引入适当的辅助系统,构建基于增广误差的自适应控制系统,克服控制输入频繁切换问题,使列车精确地追踪目标控制曲线.但当线路扰动较大时,列车运行状态收敛到要求的跟踪误差范围的快速性存在缺陷.文献[6]为防止正常运行的列车在限速区段紧急停车,设计了一种基于模型预测控制的ATO控制算法,在保证ATO控制列车正常运行情况下不会触发紧急制动的同时,提高列车运行效率和舒适度.文献[7]充分考虑系统参数模型和外部扰动的不确定性,增强控制系统的鲁棒性和自适应性,实现列车较高精度跟踪.文献[8]设计了一种反推自动控制停车器,消除了制动过程中由于模型非线性和系统时滞带来的影响.文献[9]设计了一种自适应模糊滑模控制器,通过模糊切换补偿运行阻力和外部扰动,削弱了滑模控制固有的抖振现象,实现精确停车.文献[10]采用广义预测控制算法,引入参数估计来实现列车制动系统的参数辨识,使得控制器具备了良好的抗干扰能力,且该算法具备良好的鲁棒性.

上述控制策略虽然取得了较好的控制效果,但单质点模型忽略了动车组内部纵向冲击的影响,同时,在动力输出方面,单质点模型无法根据动车组各控制单元不同的情况输出相应的控制力,存在其模型的局限性.由于动车组各单元是通过车钩缓冲装置连挂在一起,即为一个弹性系统.在动车组实际制动过程中,由于各复合控制单元在乘客人数、速度、位移等各方面的不同,使得各单元间的相互作用力也会不同,进而促使各车钩缓冲装置产生不同的拉伸或压缩情况.动车组各单元之间的车钩缓冲装置在正常载荷工况下的缓冲器行程为45～100 mm[11],累计有可能会造成较大的停车误差.

多质点模型针对各车厢各单元等效质量、速度、位移、姿态振动特性的不同来建立模型,在考虑到线路附加阻力在变坡点和变曲线点存在计算误差和车厢之间的相互作用力的同时,多质点模型能够合理的进行动力分配,弥补单质点模型的不足之处.文献[12]通过分析相邻车厢间的耦合方式,建立一种简单的高速列车多质点模型,并针对该模型的特点,设计了相应的巡航控制器,改善了列车巡航时的控制性能.文献[13]针对重载列车多质点模型,采用级联方式进行简化和转换列车模型,在模型预测控制的框架下,优化了列车运行时的各项性能.文献[14]针对高速列车多质点模型,设计了一种考虑多级牵引与制动的列车多质点单位移模型,简化了列车内部受力情况,改善了列车启动阶段和制动阶段的控制效果,但是该控制模型实质是将列车多质点模型化简为单质点模型进行控制.文献[15-16]将动车组模型中的运行阻力或车间作用力这类非线性力进行模糊化,分别将模糊预测控制器和自适应模糊滑模控制器应用到动车组多质点模型控制研究中,进一步改善了列车牵引和制动的控制精度,但是这类控制器的设计过程在很大程度上取决于专家实际工程经验,且控制器的收敛速度和实时性方面有待进一步提高.上述控制策略对模型中的车间作用力或运行阻力进行了不同程度的简化补偿或模糊化,这会使控制器计算结果与动车组实际情况存在一定误差.

基于此,本文对动车组乘车人数不同对每节车厢受力的影响以及车厢间的相互作用力进行分析,将基本运行阻力、线路附加阻力分散到各复合控制单元,建立了动车组多质点非线性动力学模型.考虑到动车组运行环境复杂多变,使得动车组非线性模型的参数具有随机性,设计参数自适应控制器,对模型中的包括基本阻力参数、车间作用力参数和线路参数等未知参数采用自适应策略,进行实时在线估计,进而对各复合控制单元进行单独有效的控制.根据输入-输出稳定性原理,证明了该控制器的渐近稳定性.得到理论分析和仿真结果一致,验证了控制算法的有效性,实现动车组高精度停车控制.

2 系统模型

基于动车组纵向动力学模型的研究中,动车组单质点模型将整个动车组简化为一个质点,这种模型易于分析,计算比较简单.与单质点模型相比,多质点模型结构复杂、计算量大,但能更好地反映动车组的实际受力和运行情况.多质点模型将每个动力单元看作一个单独的质点进行受力分析,考虑了相邻单元之间车钩力对动车组的影响,以及附加阻力在变坡点和变曲线点受其长度的影响,能够有效降低控制器的计算误差,提高动车组的控制精度.方便起见,多质点模型中第j个质点的受力情况如图1所示.

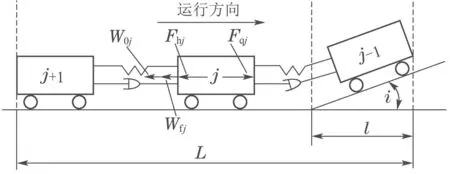
图1 多质点模型纵向受力分析图Fig.1 Longitudinal force analysis diagram of multiple unit model

第j个质点的动态力学模型表达式为

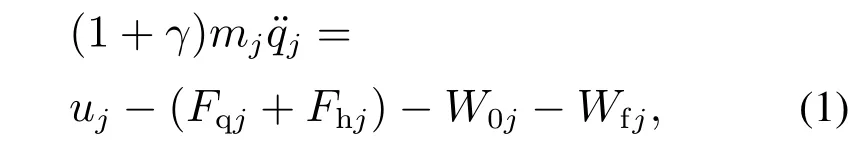
式中:uj为动车组控制输入,即输入的牵引力或者制动力,在动车组制动过程中,动车提供电制动,拖车提供空气制动.Fqj为第j个质点的前车钩力,Fhj为第j个质点的后车钩力,两者之和即为动车组各质点间的弹性耦合力;W0j为第j个质点受到的基本阻力;Wfj为第j个质点受到线路纵断面影响产生的附加阻力.

第j个质点受到的弹性耦合力的表达式如式(2)所示:

其中:k表示弹簧的刚度系数;b表示阻尼系数.

第j个质点受到的基本阻力表达式为

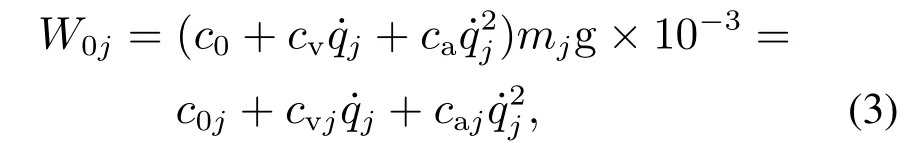
各单元受到的基本阻力,包括车轮滚动阻力、机械阻力和空气阻力,c0,cv,ca为单位基本阻力系数,这些系数会随着运行环境的变化而变化.

第j个质点受到的附加阻力表达式为

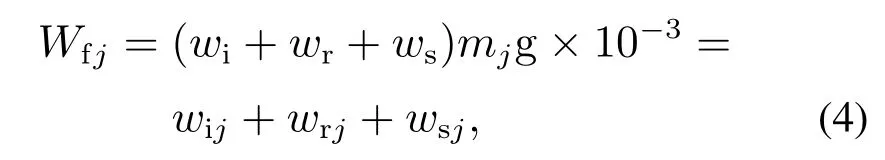
单位附加阻力包括单位坡道附加阻力wi=i,i表示坡度数;单位曲线附加阻力wr=600/R,R表示曲线半径;单位隧道附加阻力ws=0.00013Ls,Ls表示隧道长度.各单元受到的单位附加阻力基本相同,文中主要考虑惯性参数对附加阻力的影响.

动车组制动控制方式通常采用电制动和空气制动对列车进行复合制动,本文针对编组动拖比为1:1的动车组,即1M1T作为电制动与空气制动的协调分配单元.以复合控制单元形式进行动车组编组可以使得动车组运行总能耗最低,同时,这样的编组在动车组改编为2M2T或4M4T的编组形式时,不会影响动车组的功率配置[17].本模型对动车组进行受力分析,将动车组中的1M1T作为一个独立的控制单元,为描述方便,将动车组在牵引与制动阶段的动态模型统一表述为

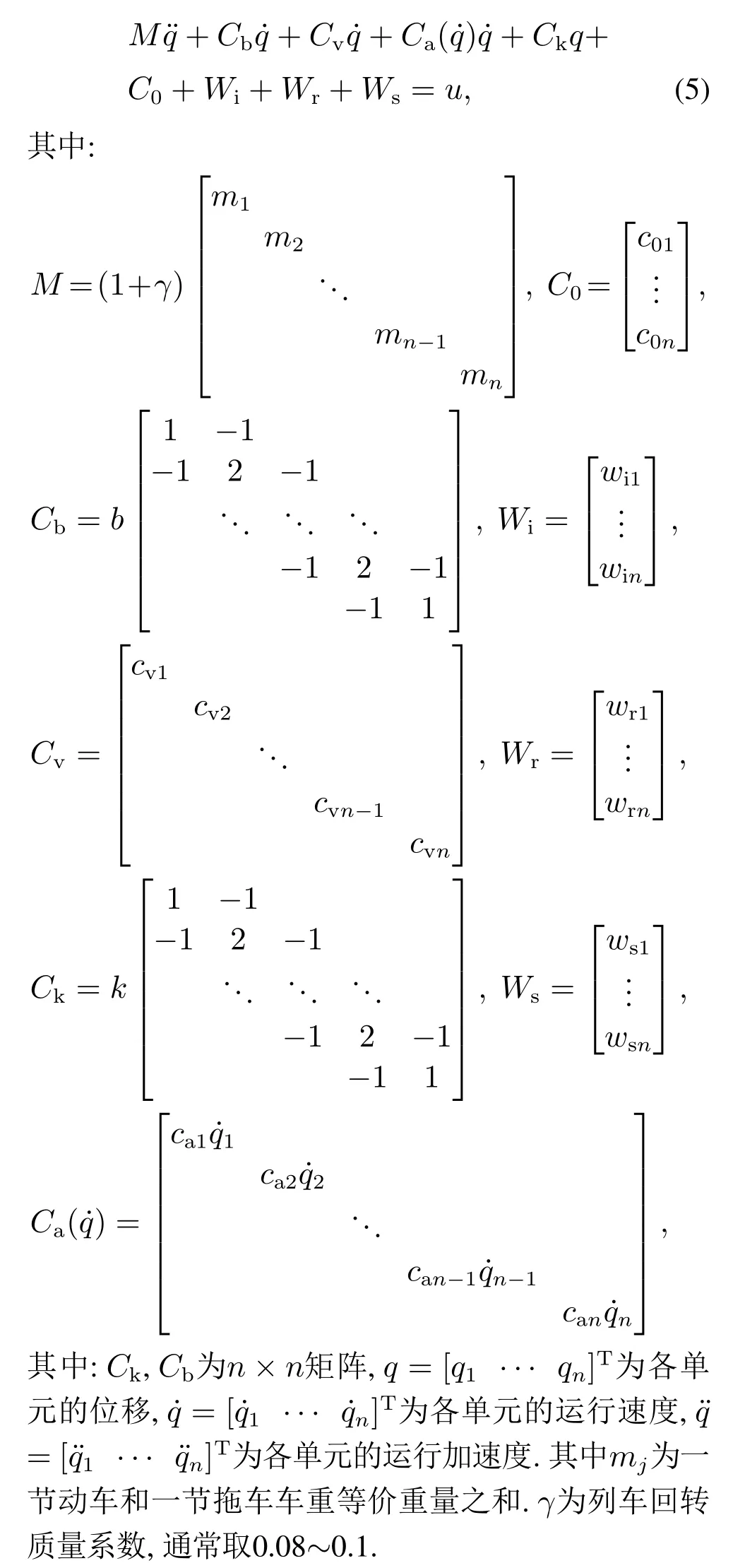
3 控制器设计

在动车组实际运行过程中,由于诸多环境因素和动车组系统自身的影响,使得该系统存在随机性,于是,动车组基本阻力系数和列车间弹性耦合力系数的准确信息很难获得,甚至不可能测得.本文设计的控制器直接考虑相关参数的未知性以及现有研究中被忽略的动车组牵引与制动特性,建立动车组速度和位移跟踪控制的自适应控制策略,对各参数的数值进行实时估计.控制器设计的任务是跟踪时变的位移期望轨迹qd(t)和速度期望轨迹d(t),定义其位置跟踪误差为式(6)所示,速度跟踪误差为式(7)所示:

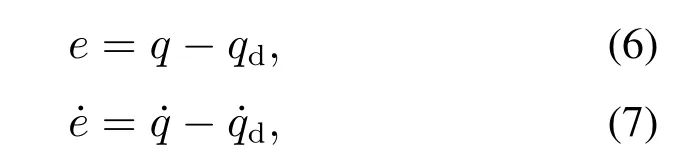
定义一个趋近于期望速度的变量如式(8):

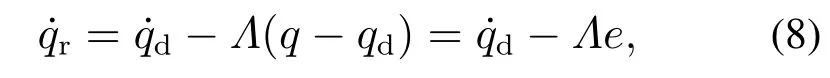
式中Λ为一正定的常数对角矩阵,矩阵中的元素由设计者根据被控对象的模型不同可自由选择.

为了便于实现李雅普洛夫函数对时间的导数半负定,选取参数的估计律为式(12)所示.其中,Γ为正定的常数对角矩阵,矩阵元素根据设计者自由选择.

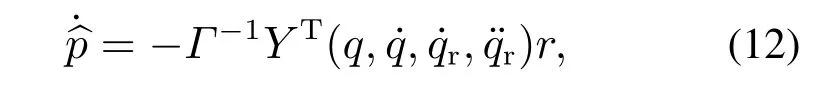
式(12)与控制律(9)一起构成了所要设计的自适应控制方案.

4 稳定性分析

所以闭环系统方程由式(11)和式(13)描述,定义函数V(t)如式(14)所示:

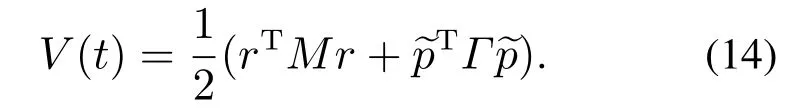
由M及Γ的正定性知V(t)≥0.由式(11)和式(13)知,沿闭环系统轨迹如式(15)所示:

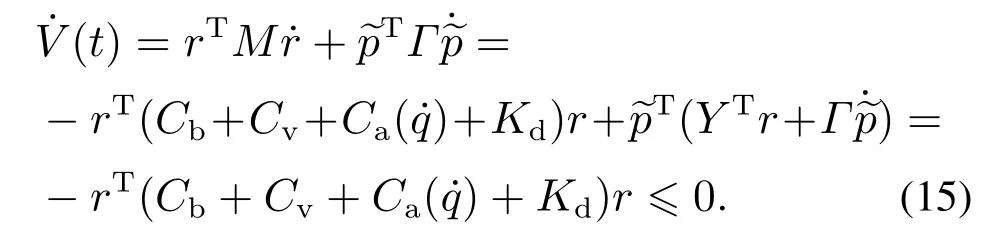
由式(15)表明沿式(11)(13)描述闭环系统的轨迹V(t)在R+上单调有界,故存在有限极限V(∞)且

5 仿真结果分析

本节基于3辆动车3辆拖车编组的地铁动车组的实际数据,应用数值仿真软件对动车组精确停车自适应控制方法的有效性进行仿真验证.动车组的相关数据设置如下:各控制单元定员载重为175 t,第1个复合控制单元实际载重为175.1 t,第2个复合控制单元实际载重为172.5 t,第3 个复合控制单元实际载重为173.8 t,各复合控制单元的估计初始载重分别为178.2 t,170.6,179.5 t,质量回转系数γ取0.08,其余相关仿真参数如表1所示.

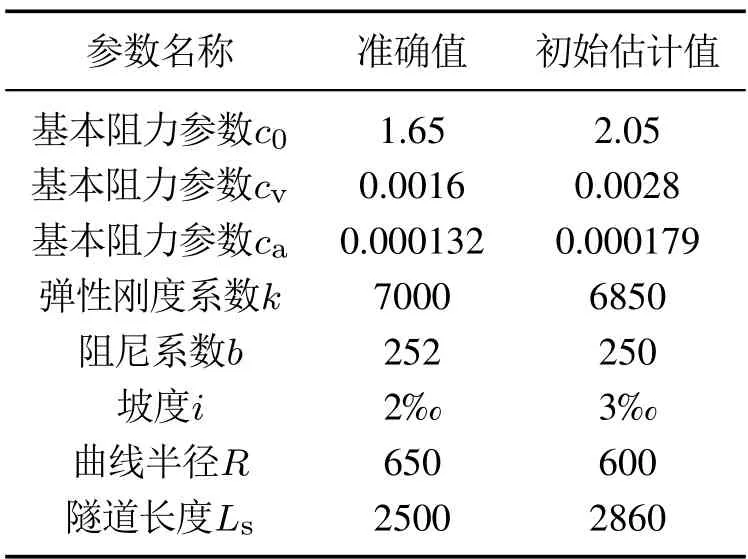
表1 列车运行基本参数Table 1 Basic parameters of train operation

同时,将设计过程中的正定矩阵Λ,Kd,Γ分别设计为Λ=diag{54,31,53.6},Kd=diag{45,30,50},Γ=diag{0.05,0.05,0.05,10,2,0.7,1,10,1,0.26,2},动车组期望的制动初始速度为72 km/s.动车组运行追踪效果如图2-9所示.

由图2-4可见,3个独立的复合控制单元在载客人数不同,受力不同的情况下,动车组实际运行曲线能够很好地追踪期望运行曲线.在制动开始阶段,由于动车组实际制动位置、制动速度与期望制动位置、制动速度存在误差,以及动车组基本运行阻力系数存在误差,使得动车组各控制单元的实际运行轨迹与期望运行轨迹之间存在误差.随后,自适应控制器在线估计各未知参数数值,使得动车组实际运行轨迹快速地追踪期望运行轨迹.图5-6分别给出动车组各单元的位移误差和速度误差,仿真结果表明,各控制单元最终停在距离目标点±5 cm范围内,满足动车组停车误差在±30 cm的要求,并且达到了很高的停车精度.同时,各复合控制单元的速度误差在0.6 m/s以内,且波动次数较少.

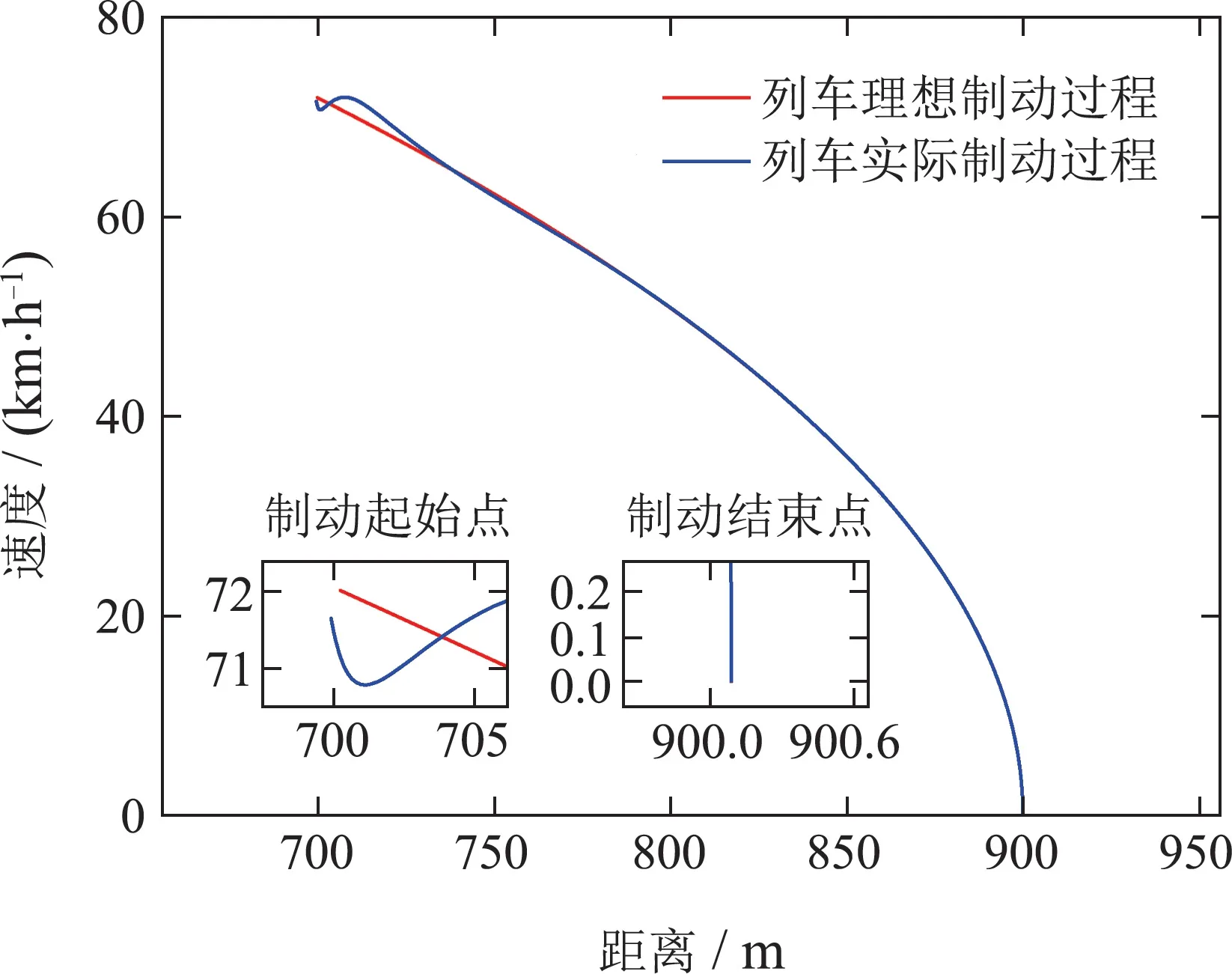
图2 第1节点制动速度-距离(V-S)曲线Fig.2 Braking velocity-distance curve of the first node

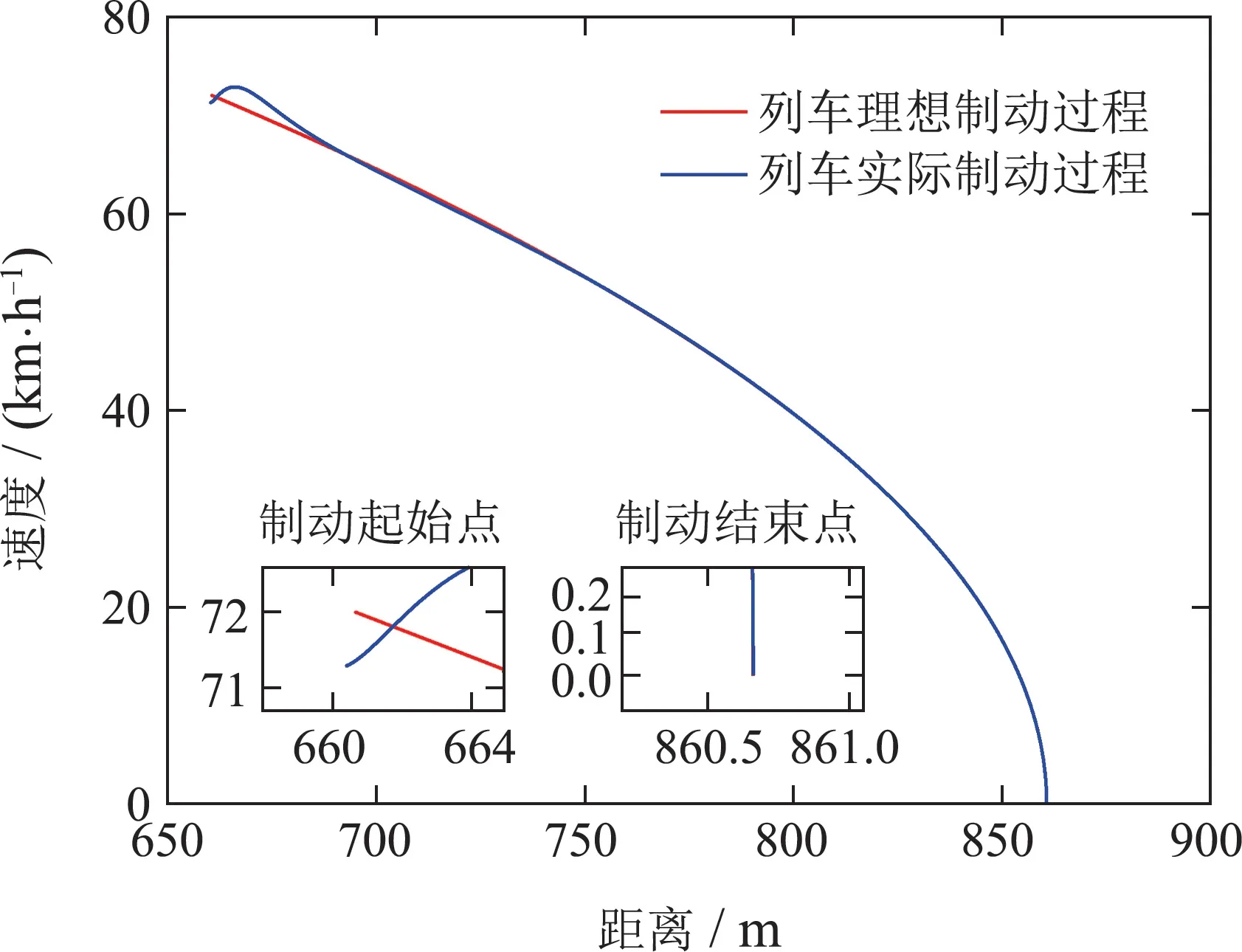
图3 第2节点制动速度-距离(V-S)曲线Fig.3 Braking velocity-distance curve of the second node

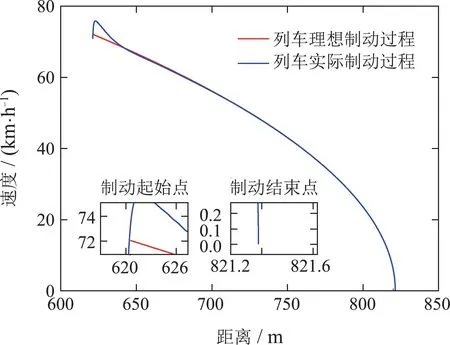
图4 第3节点制动速度-距离(V-S)曲线Fig.4 Braking velocity-distance curve of the third node

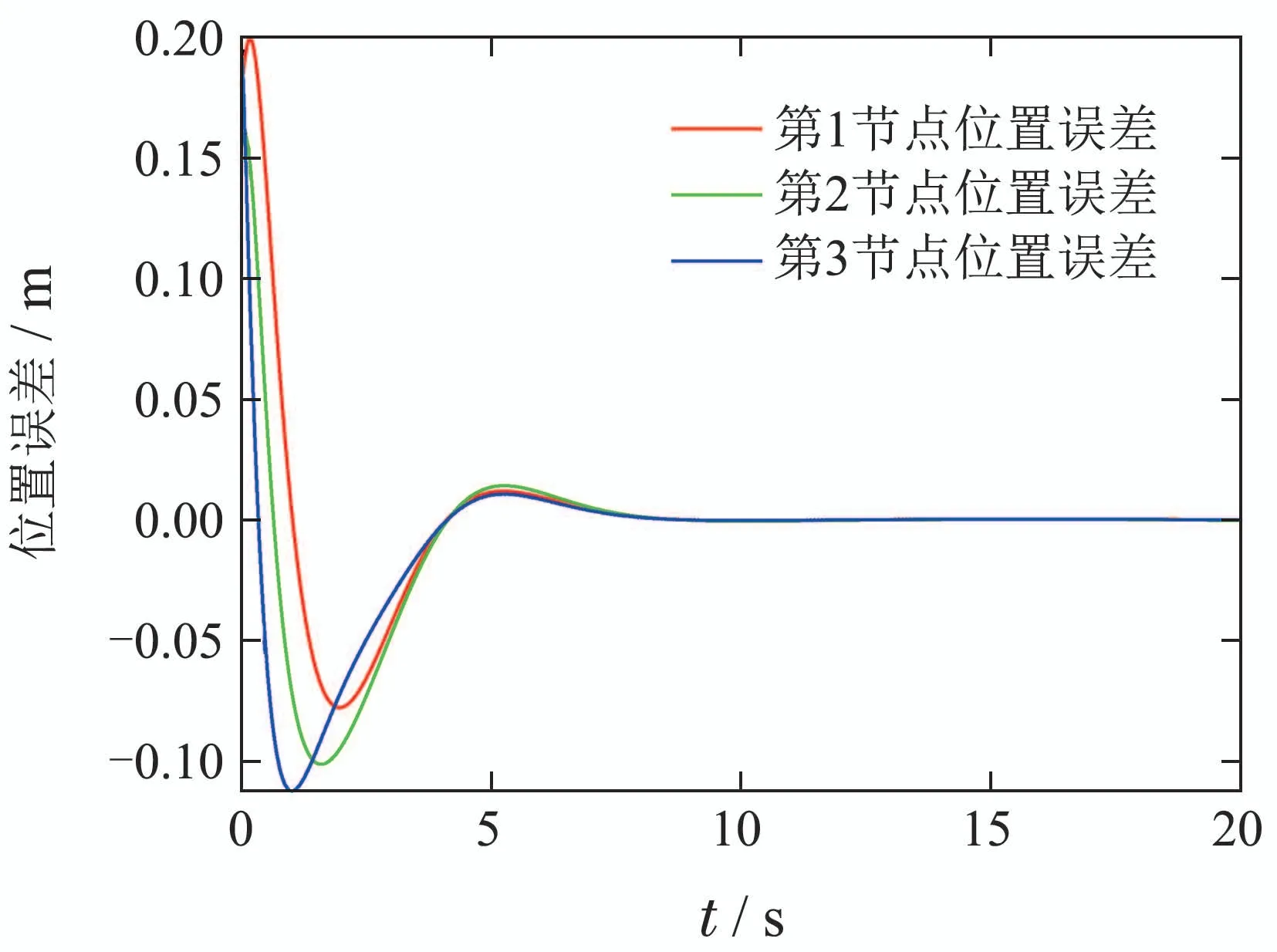
图5 位置误差曲线Fig.5 Error curve of position

相比于文献[4],本文所设计的自适应控制器收敛速度更快,且各单元的速度误差和位移误差更小,控制精度更高.相比于文献[14],本文在仿真的初始时刻,对各单元设置不同的位移误差和速度误差,仿真结果表明,在初始扰动的影响下,各控制单元在初始时刻存在较大误差,但最终各单元停在距离目标点极小范围内.相比于文献[15],本文中动车组各单元速度误差的波动较为光滑,没有发生速度的跳变.综合来看,本文所设计的控制器具有收敛速度较快,控制精度高等优点,在提高动车组乘坐舒适性的同时,能够有效提高乘客上下车的效率.

根据图7显示,在列车开始制动时,由于各复合控制单元设置的相对位置和相对速度存在较大差值,此时,车厢间的纵向冲击较大,各控制单元之间的车钩力较大.随着各单元协调控制,使得各控制单元的相对位移和相对速度逐渐趋于0,进而使得各控制单元间的车钩力趋于0.在车钩力低于车钩所能承受的最大车钩力的同时,图7表明动车组多质点模型用于动车组精准停车控制更具有优势.

由图8可以看出,动车组在运行过程中,自适应控制器能在不同时刻分配不同的制动力给各复合控制单元,更符合动车组实际制动情况,控制器实时调节制动力的大小,能够实现动车组制动的无级精确控制[20].

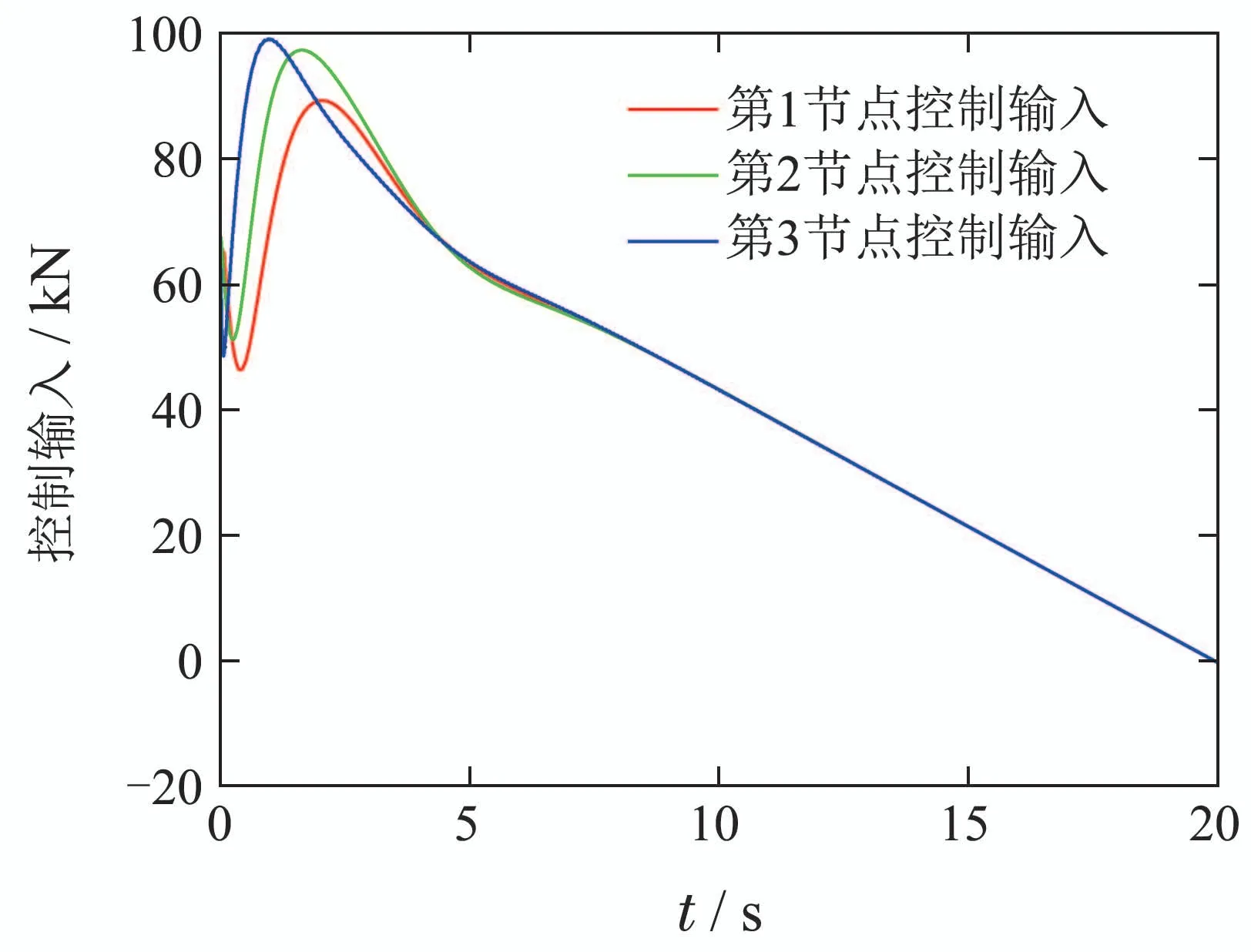
图8 控制输入Fig.8 Control input

图9为控制器中参数估计值的变化特性仿真图,从仿真结果可以看出,控制器中的各参数不断调整,随着系统渐近稳定,并收敛到固定值.该结果表明,本文设计的控制器能够实时调节控制器中参数的估计值,有效应对动车组运行过程中的模型参数的随机和未知性,实现动车组系统的高精度控制.

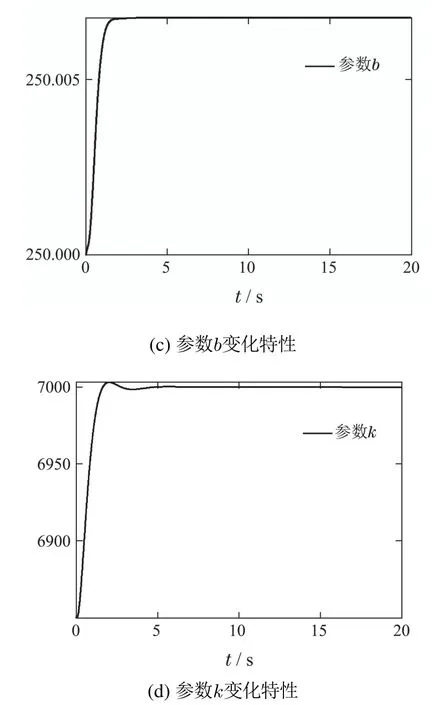
图9 参数变化特性曲线Fig.9 Characteristic curve of changing parameter

6 结论

首先,本文充分考虑动车组的乘客人数、速度、位移、车厢长度对每节车厢的受力的影响,建立一种以复合控制单元为基础的动车组多质点非线性动力学模型,对每一个复合控制单元分配不同的控制输入,协调控制各单元,使各控制单元减速一致,提高了动车组制动过程的乘坐舒适性.

其次,针对动车组精确停车±30 cm之内的要求,基于动车组多质点模型,设计多输入多输出自适应控制,对未知参数进行实时在线更新.设计的控制方法以很高的精度控制动车组精确停车的同时,收敛速度较快.

最后,应用仿真软件对所提的控制算法进行验证,通过分析,验证了所提算法的有效性,且所设计的模型和算法很符合动车组的实际运行情况.针对动车组模型参数未知的情况,现已做出了较为深入的研究,但是,在动车组在运行过程中,列车牵引或制动执行单元故障,也会影响动车组正常运行,后续将会对这类情况进行分析,将部分动力执行单元故障的动车组视为欠驱动模型,依据欠驱动控制[21]对动车组的运行控制进行研究.