控压钻井系统井下不确定参数与未知状态估计

徐宝昌,吴 楠,孟卓然

(中国石油大学(北京)信息科学与工程学院,北京 102249)

1 引言

在深部复杂地层钻井过程中,井下存在异常高压、易垮塌、漏失等复杂作业条件,井底压力的安全窗口窄,安全作业风险高[1-2].同时,近年来我国发现的特大型油气田均处于超过4500 m的深部复杂地层,井下变量的测量受限于仪器性能,可测信息少且传输速率低,传统随钻测量所获取的井底压力需要数十秒才能传至地面,并且当工况迁移或存在未知干扰时,井下部分重要参数丢失[3-4].由于井下可测信息少且实时性差,往往导致控制滞后,进而影响钻井过程安全.例如在塔里木库车山前高压盐水层、高压裂缝性地层等复杂地层钻井实践中,因井底压力波动导致发生溢流、漏失的井数占总井数的25%以上,年均损失数亿元[5-6].

在控压钻井(managed pressure drilling,MPD)系统中,控制系统通常包括两部分:1)用于实时估计井下不确定参数及未知状态的水力学模型;2)通过节流阀调节井口回压的反馈控制算法.其中水力学模型是决定MPD系统控制精度的主要因素,然而由于井下工况复杂,水力学模型中存在无法测量的参数与状态.因此,研究可靠的参数估计方法对MPD井下不确定信息进行实时估计,对保证安全高效钻井具有重大意义.

动态系统参数不确定性和外部扰动可以看作系统的未知输入[7-11],学者们最初仅考虑抑制未知输入进而对系统状态进行准确估计[12-15],在此基础上,研究了未知状态和不确定参数同时估计的自适应观测器设计问题,并针对非线性系统将自适应观测器大致分为联合状态参数观测器和自适应状态观测器两大类[16-17].目前,国内外学者对井下不确定参数和未知状态估计的观测器设计方法已经进行了一定的研究工作.Zhou等[18-20]基于简化的水力学模型,通过设计状态观测器,估计钻头处流量和井底压力,设计了井底压力非线性控制律.该方法可以在线估计未知状态.徐宝昌等[21]以提前预判气侵工况为目标,应用自适应观测器理论,以实际立压、回压数据作为观测器输入,对未知井底压力与井底流量进行估计.Habib等[22-23]提出了一种基于无迹卡尔曼滤波和未知输入估计理论的观测器,同时估计井底钻头流量和气侵,并以此为依据检测与评估异常工况.Stamnes等[24]利用Lyapunov分析和非线性坐标变换,给出了一类非线性系统降阶自适应状态观测器的构造方法.该方法允许未知状态中同时存在不确定参数以及非线性项,但构造这种自适应状态观测器的条件十分严格,需要求解一个特定的偏微分方程组才能得到其更新率.

与基于观测器匹配条件构造观测器的方法不同,现有研究成果大多是根据特殊的坐标变换方法构造自适应观测器,其构造条件十分严格,且难以应用于其他非线性系统.因此,本文针对MPD这类非线性系统,提出一种从观测器匹配条件出发的观测器设计新方法.观测器匹配条件于文献[25]中首次提到,该条件对观测器设计中的不确定参数解耦具有重要意义,基于此条件已出现了多种观测器设计方法[17,26-28].其中,文献[26]针对存在不确定参数的线性和非线性Lipschitz系统,讨论了当观测器增益和系统输入存在干扰时参数和状态的估计问题,设计了非线性非脆弱比例积分滤波误差自适应观测器.文献[27]针对常微分方程组中状态和参数值的渐近重构问题,提出了一种参数化解决方案,即将不确定参数作为状态和时间的非线性参数化函数.文献[28]设计的自适应观测器可从稳定性证明中消除限制性耗散条件,并将观测器增益求解问题转化为一个线性矩阵不等式(linear matrix inequality,LMI)的可行性问题.

文献[26-28]方法的共同之处在于其非线性系统结构都可以满足观测器匹配条件,然而对MPD系统这类未知状态中含有不确定参数的非线性系统,传统的观测器匹配条件并不能对其不确定参数进行解耦.因此,本文在学者Stamnes等人的研究成果[24,28]基础上,针对钻井系统这类未知状态中含有不确定参数的非线性系统,提出了一种新的自适应观测器设计方法.该方法对传统观测器匹配条件进行改进,使其能够对MPD系统中的不确定参数进行解耦.并在此基础上,用构造性方法设计了一种联合估计不确定参数和未知状态的自适应观测器,证明了持续激励(persistent excitation,PE)条件下未知状态及不确定参数的全局渐近稳定.最后,基于LMI方法求解观测器增益,优化了观测器设计过程,并提高了系统鲁棒性.仿真实验结果表明,本文所提方法能够在MPD系统同时存在不确定参数与未知状态的情况下,准确地估计井下不确定参数与未知状态,且对井下环空摩擦积分和井底流量的估计具有更快的收敛速度以及较好的鲁棒性.

2 系统描述

本文采用的简化水力学模型,井筒本身以及一系列钻井设备都包含在该模型中,如钻井泵、钻杆、钻头、环空以及节流阀等,如图1所示[21].

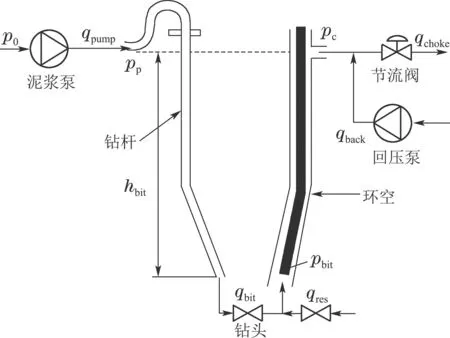
图1 控压钻井系统简化模型Fig.1 Managed pressure drilling system simplified model

该模型将井筒分为钻杆和环空2个独立的单元,并通过钻头将这两个独立单元连接起来.由质量守恒以及动量守恒定律,钻井系统的数学模型可表示为[18]:

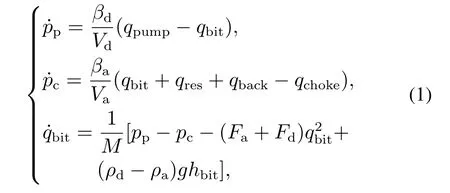
其中:βa,βd分别为环空和钻杆的体积模量;Va,Vd分别表示环空和钻杆体积;hbit为井深;ρa,ρd分别代表环空和钻杆中的流体密度;M为环空和钻杆内流动方向上单位截面密度的积分;Fa,Fd分别是环空和钻杆中摩擦积分;pp表示泥浆泵出口压力;pc为井口回压;qbit代表井底流量;qpump,qback,qchoke分别为泥浆泵出口流量、回压泵流量和节流阀出口流量;qres表示地层侵入流体流量.注意式(1)中的Fa,Fd,ρa,ρd为难以获取准确数值的井下参数,qbit为未知的井下变量.针对式(1)模型,考虑如下形式的非线性系统:

假设1函数Ω(y,u)在其定义域上是连续的,Φ(x)和Ψ(x)关于x满足Lipschitz条件,存在正实数γ1和γ2使下式成立:

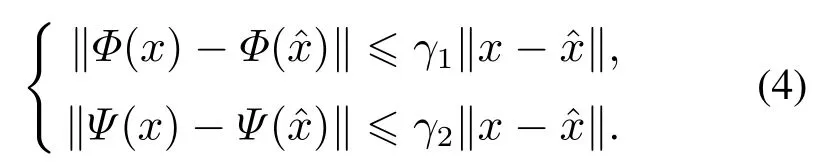
假设2不确定参数θ为有界常数,存在已知正实数γ3使下式成立:

注1需要指出的是,假设1的应用取决于式(4)的Lipschitz条件是局部还是全局地满足.文献[29]中指出任何=f(x,u)形式的系统,如果对x连续可微,其结构都可以表示为线性部分加上非线性部分,且至少在局部满足Lipschitz条件.

引理1[30]存在矩阵P=PT＞0及F使得等式ETP=FC成立,当且仅当

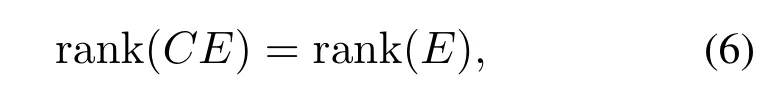
式(6)即观测器匹配条件,表示rank(E)＜rank(C),即q ＜p.对于大多数情况下的非线性系统(2),满足观测器匹配条件意味着向量Ψ(x)θ的所有项,包括不确定参数,至少在q个可测状态中显式出现.该条件可通过对系统(2)中的输出y的一阶导数来理解:

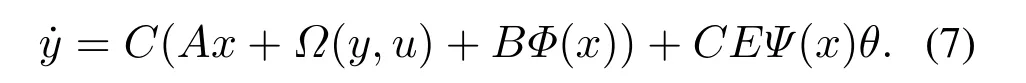
由式(7)可知,如果满足观测器匹配条件,系统(2)和式(7)中Ψ(x)θ的系数矩阵具有相同的秩,即系统(2)中出现的Ψ(x)θ的所有项也会出现在式(7)中.

然而对于一些类似本文MPD系统的非线性系统,容易验证其结构不能满足观测器匹配条件.因此,传统的自适应状态观测器在这些系统中是不可实现的.本文的目的在于,提出一种新的观测器构造方法,即对原有观测器匹配条件进行改造,使其被一些不满足观测器匹配条件的系统所满足.

3 自适应观测器设计及收敛性分析

本节针对不确定参数存在于未知状态的系统(2),提出了一种新的自适应观测器设计方法.与传统的自适应观测器设计一样,该方法将不确定参数与测量输出的关系表述为矩阵等式,并在此基础上构造自适应观测器.

3.1 自适应观测器设计

为了更好的表述系统(2)的结构以及构造自适应观测器,提出如下假设.

假设3矩阵A,B,C和E满足

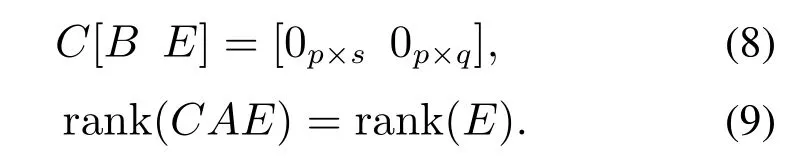
从相对阶的角度来看,式(8)意味着从输出到Φ(x)和Ψ(x)θ的相对阶至少为2,即不确定项不直接存在可测输出中,需要对输出求两次导数才能得到关于Φ(x)和Ψ(x)θ的表达式.式(9)则是在常规观测器匹配条件的基础上进行了改造,其表示rank(E)≤rank(C),即q≤p.

注2文献[24]以一种特殊的标准形式考虑了一类非线性系统,其不确定参数和未知非线性项存在于未知状态中.不同于假设3中通过相对阶来确定不确定参数位置的方式,文献[24]中的标准形式并没有将不确定项相对于输出的精确位置表示出来.然而,对于文献[24,28]中的系统,可以很容易的验证其结构满足假设3.

当系统满足假设3时,可提出如下引理.

对满足引理1的非线性系统(2),一种经典的自适应观测器设计形式如下[28,31-32]:

其中:L ∈Rn×p为观测器增益,ρ是正常数,F ∈Rq×p为待定的常数增益矩阵.然而,当非线性系统不满足引理1时,无法使用增益矩阵F来构造观测器.

基于上述考虑,对于满足假设1-3的系统(2),利用引理2中的矩阵H来替代引理1中的增益矩阵F,并引入一个中间变量W用于表示不确定参数θ的估计值.设计如下形式的类Luenberger观测器来进行状态和参数估计:

3.2 收敛性分析

观测器(15)的收敛性证明需要基于如下引理及推论.

其中:η为一个正的标量,求解式(28)需使η最小化.同时求解线性矩阵不等式(27)和式(28)即可得到矩阵H,G和P.

将提出的自适应观测器设计方法总结为如下步骤:

步骤1假设系统中未知函数Φ(x)和Ψ(x)在其定义域上满足局部Lipschitz条件,并根据其定义域取Lipschitz常数γ1,γ2;

步骤2根据不确定参数θ的取值范围设定Lipschitz常数γ3;

步骤3利用引理2中矩阵H,G的性质,设计观测器(15)中的参数估计方程=W+ΓΨT()Hy;

步骤4通过LMI求解矩阵H,G,M和P,并根据L=P-1M计算出观测器增益矩阵L;

步骤5设定仿真模型初始条件,利用步骤4计算出的矩阵参数,使用观测器(15)估计x和θ.

4 仿真分析

为验证本文所提出自适应观测器的有效性,本节给出了基于MPD模型(1)的仿真结果.仿真中的模型参数与初始条件设置均与文献[18]中实验平台的参数相同,模型参数如表1所示.

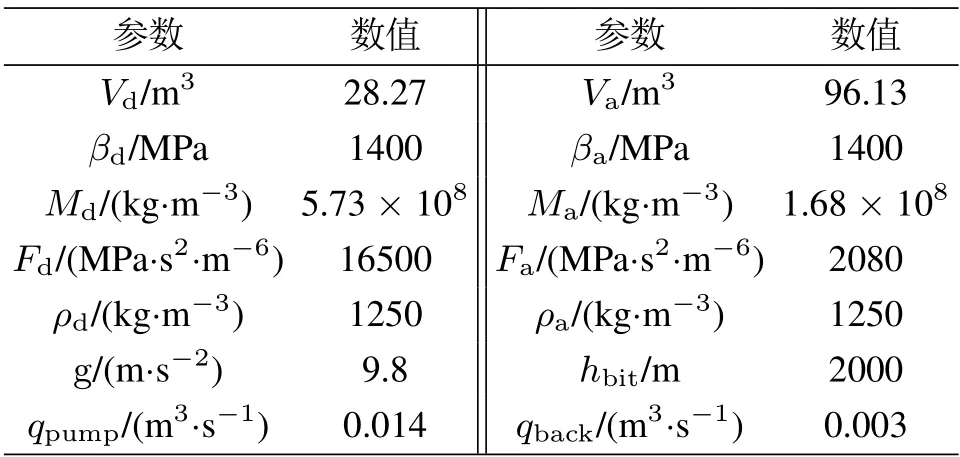
表1 钻井数据Table 1 Drilling data

由于实际控压钻井过程中控制输入Ω(y,u)决定输出中的井口回压,考虑当输入Ω(y,u)存在均值为0方差为1的噪声时进行仿真,仿真结果如图2-5所示.图2为泥浆泵出口压力、井口回压和井底流量3个状态的估计值和真实值,图3为井底流量的估计误差,图4为不确定参数的估计值和真实值,图5为不确定参数的估计误差.从图2和图3可以看出,本文所提的自适应观测器可以保证井底流量的估计值在5 s内收敛到真实值,并在整个仿真过程中表现出了良好跟踪性能.从图4及图5可看出,本文方法能够在5 s内实现对系统中不确定参数的准确估计.

图2 状态估计值和真实值Fig.2 State estimates and true values

图3 井底流量估计误差Fig.3 Bottom-hole flow estimation error

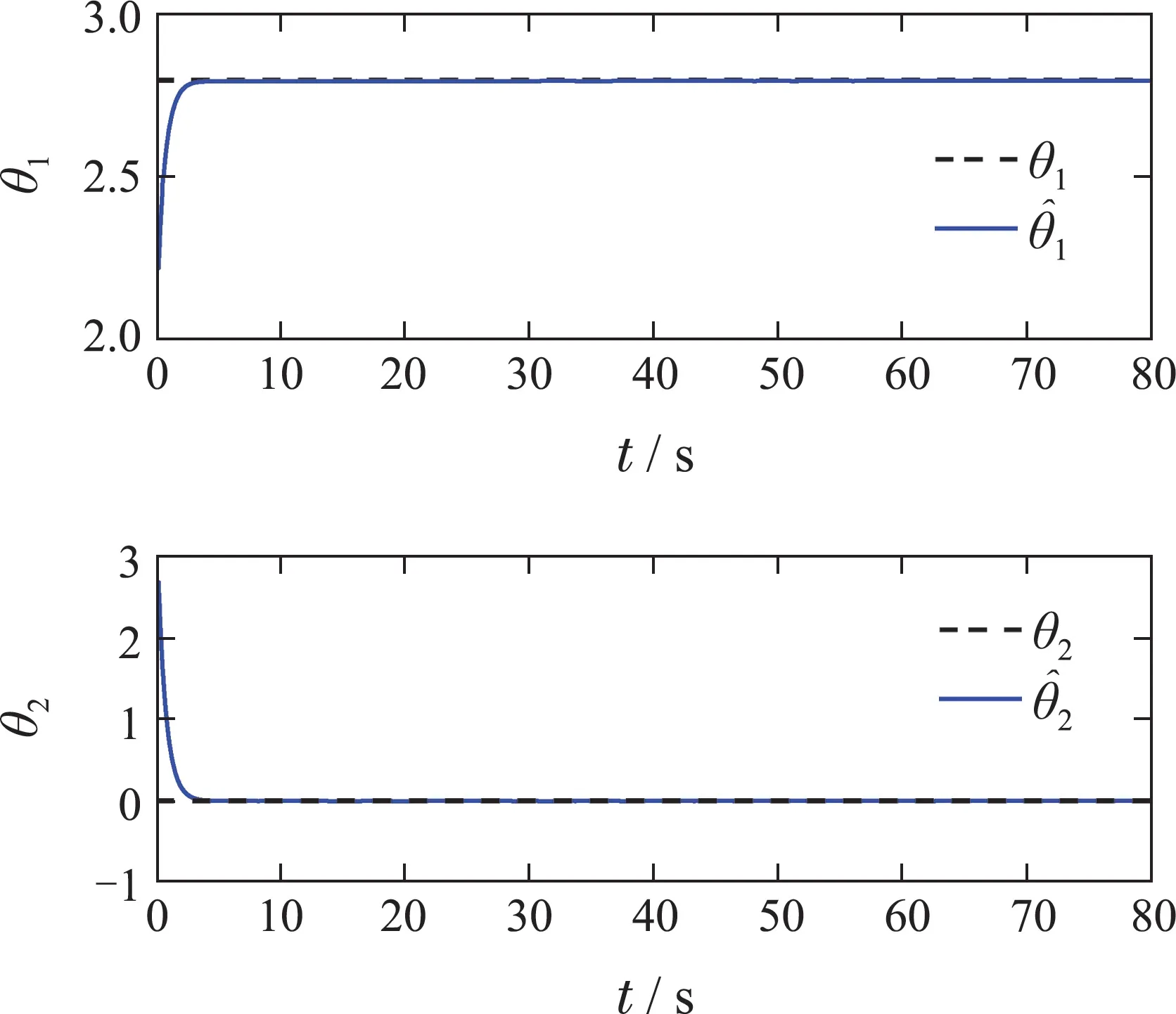
图4 不确定参数估计值和真实值Fig.4 Uncertain parameter estimates and true values

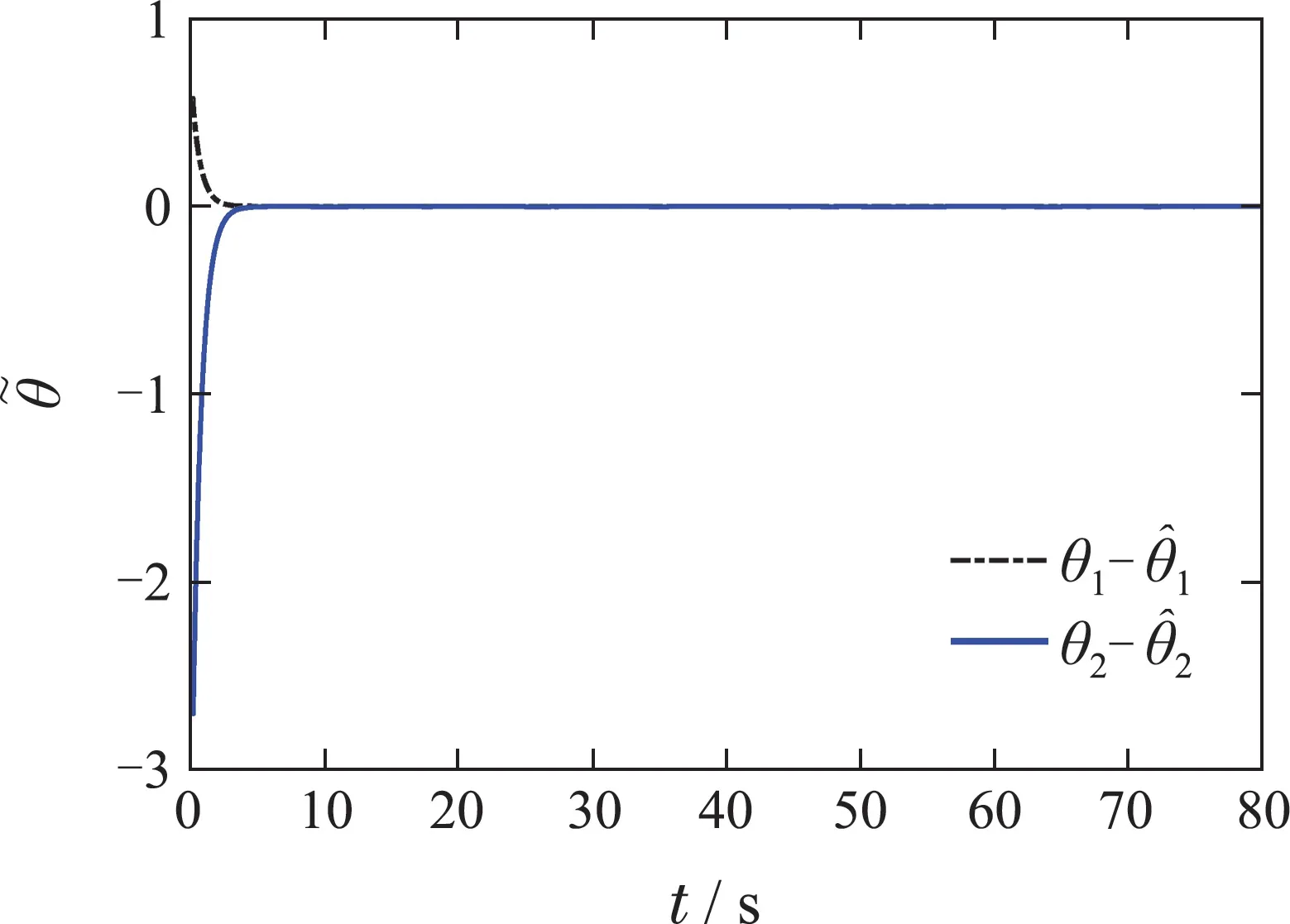
图5 不确定参数估计误差Fig.5 Uncertain parameter estimation errors

文献[21]中,自适应观测器的增益矩阵需要人为给出,繁琐的调节过程限制了该方法在实际钻井过程的应用.本文所提出观测器的增益矩阵则依赖于LMI求解,因此当MPD系统建模存在误差而增益矩阵不变时,分析观测器的鲁棒性可检验本文方法是否具有实际意义.

实际控压过程中,由于雷诺系数Re的取值变化影响Fd,从而造成建模误差[21].本文模型中Re取值为2×105,而实际控压钻井过程中Re的变化范围为5×104～6×105,假设由于Re取值不准导致建模参数Fd存在20%误差,取同样的观测器增益矩阵进行仿真,观测效果如图6-7所示.可以看到,当Fd存在20%误差时,本文设计的自适应观测器对θ1的估计有一定误差,但仍能准确的估计井底流量以及θ2.其原因是参数θ1和Fd在MPD系统中都是作为井底流量的系数,具有相同的作用.因此,当Fd存在误差时,观测器可以通过调整θ1的估计值来保证井底流量及θ2估计的准确性,即具有较好的鲁棒性.

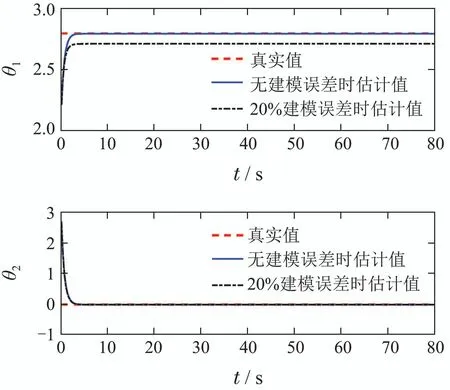
图6 不确定参数估计值和真实值Fig.6 Uncertain parameter estimates and true values

图7 井底流量估计误差Fig.7 Bottom-hole flow estimation error

此外,为了证明本文方法的优越性,与文献[21]中构造坐标变换设计自适应观测器的方法进行了比较分析.在同样的模型参数及初始条件下,文献[21]的仿真结果如图8-9所示.与图2-5对比可知,本文方法在10 s内即可令不确定参数和未知状态迅速收敛至真实值,而文献[21]方法中不确定参数和未知状态收敛至真实值的时间均超过100 s.可见,本文在观测器增益矩阵上的设计优于文献[21]中人为给定观测器增益的方法,在收敛速度上具有明显的优势.

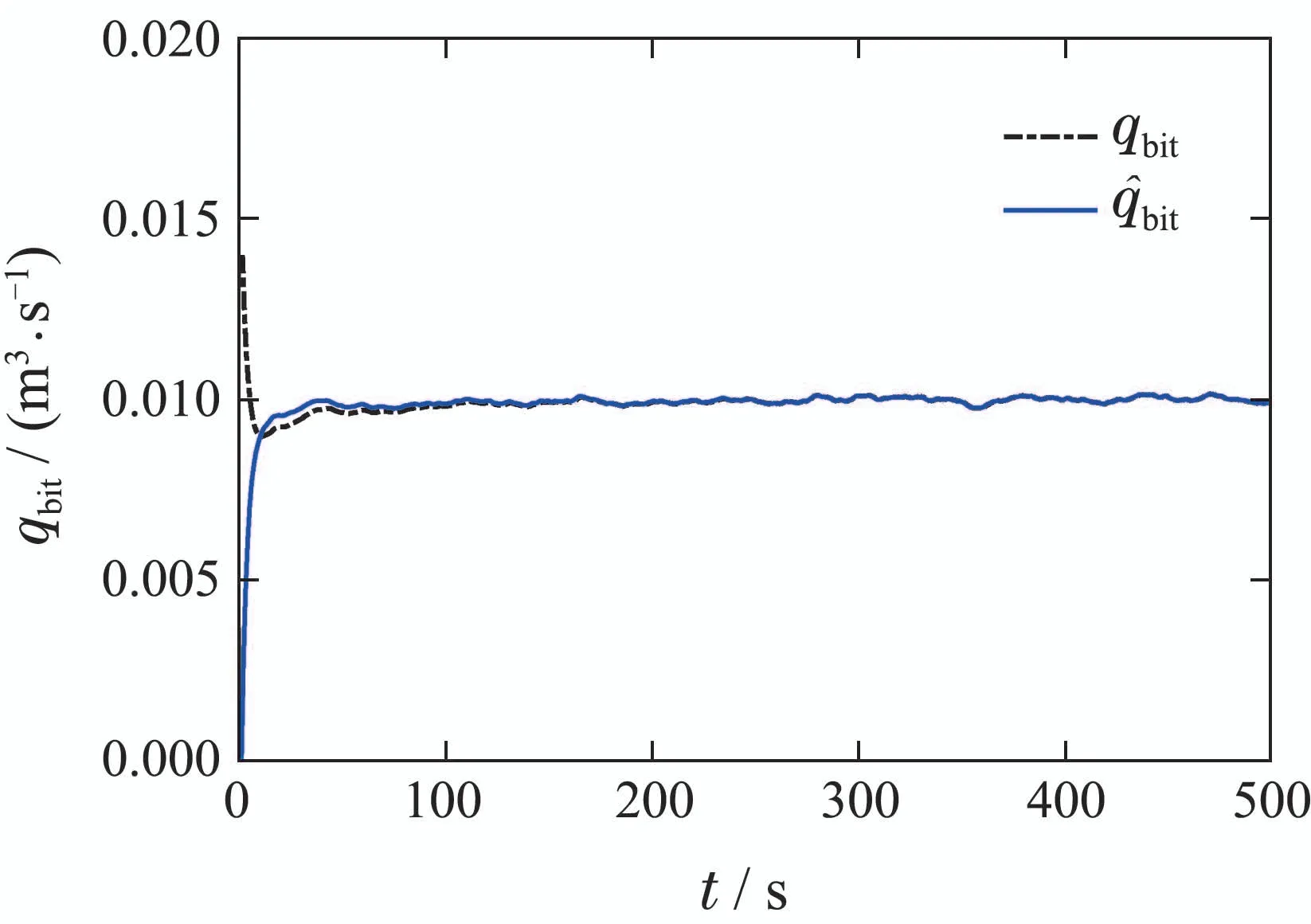
图8 已有方法对井底流量的估计效果Fig.8 Estimation effect of existing methods on bottomhole flow

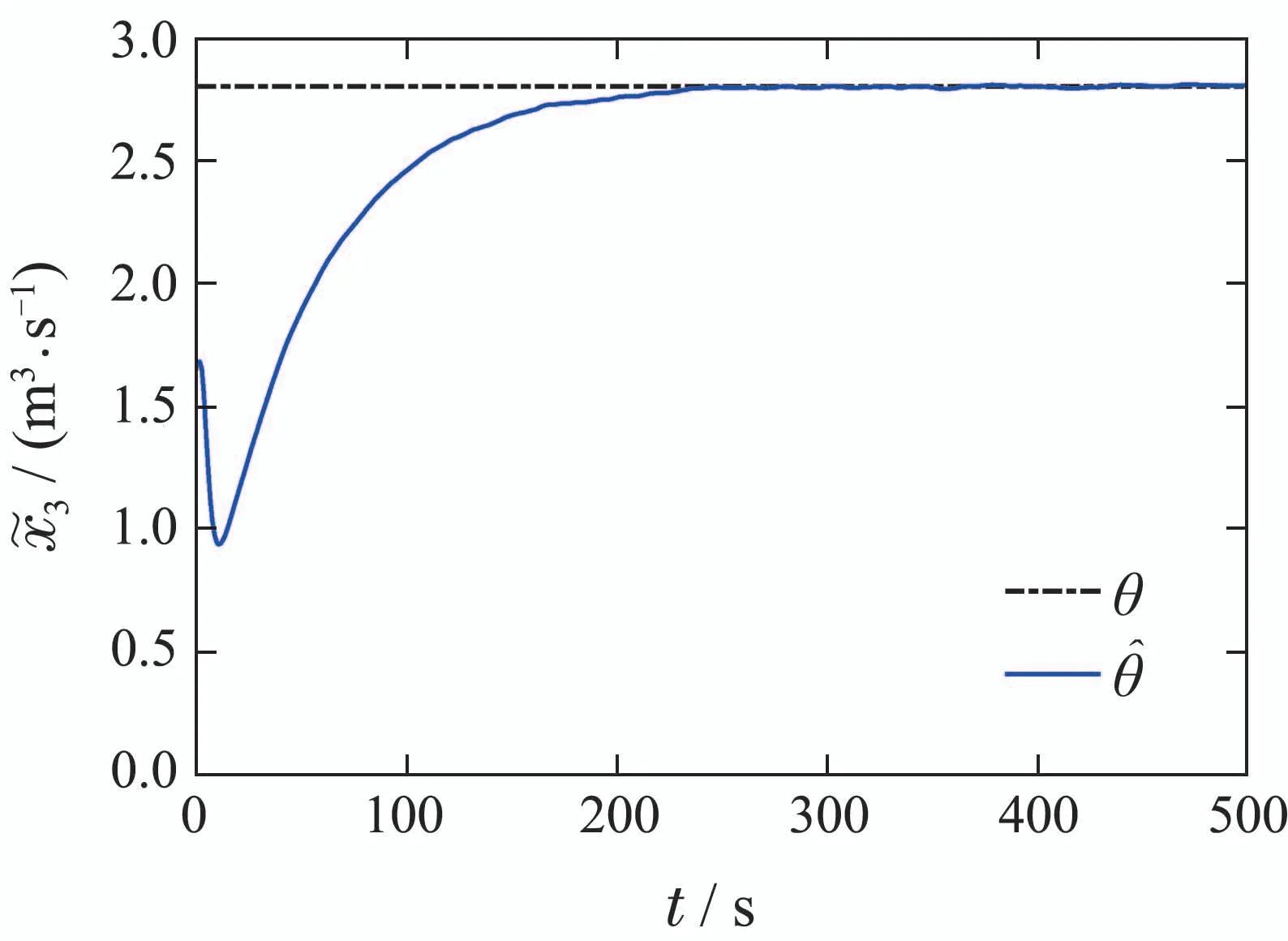
图9 已有方法对不确定参数的估计效果Fig.9 Estimation effects of existing methods on unknown parameters

5 结论

本文针对控压钻井系统这类未知状态中含有不确定参数的非线性系统,提出了一种基于新的观测器匹配条件的自适应观测器设计方法,用于处理传统观测器匹配条件不满足时的不确定参数和未知状态同时估计的问题.文中通过Lyapunov稳定性理论证明了系统状态和参数的渐近稳定性,并将观测器增益计算问题转化为LMI优化问题.仿真实验表明,本文方法能够快速且精确地跟踪系统不确定参数以及未知状态.