带有混合时滞的切换系统的耗散性分析与控制
解红珍,宗广灯,杨 东
(曲阜师范大学工学院,山东日照 276826)
1 引言
在当代日益复杂的工业过程中,由有限个连续动态和离散变量组成的切换系统凭借其强大的建模能力在实际系统中得到了广泛应用,例如:化工过程控制系统、网络控制系统和电力系统等[1].考虑在切换信号受约束情况下的稳定性分析与控制综合是研究切换系统基本且重要的问题[2].目前,设计切换信号的方法多种多样,如:公共Lyapunov 函数方法、单Lyapunov函数方法、多Lyapunov函数方法等[3].
在实现网络控制、电力系统控制等过程中,由于信号传输速度的限制,不可避免地会出现时滞现象[4].时滞的存在往往会使系统性能变差甚至直接导致系统不稳定.因此,考虑时滞对切换系统的影响,并对其稳定性性能进行分析与控制综合具有重要的理论价值与实际意义.为了获得理想的性能,许多学者对有关带有时滞的切换系统进行了研究并提出了相关技术与方法,例如:Jensen积分不等式方法[5]、自由加权矩阵方法[6]、Wirtinger不等式方法等[7].
值得注意的是上述的研究都是基于稳定子系统之间的切换,而在实际中会遇到具有不稳定子系统的切换系统[8].为了合理地利用这些不稳定子系统,许多学者对此开展了大量的工作.文献[9]利用平均驻留时间的方法设计了一种慢切换规则来稳定一类具有不稳定子系统的切换系统.近几年,在切换中引入了一种模态依赖平均驻留时间方法,以更灵活地释放平均驻留时间的限制,得到了具有缓慢模态依赖平均驻留时间切换策略的稳定性条件[10].文献[11]利用模态依赖平均驻留时间切换的方法实现了离散时间的切换线性系统指数稳定性.文献[12]针对带有不稳定子系统的线性切换奇异系统,利用模态依赖平均驻留时间的方法得到了系统的稳定性判据.但值得指出的是对于时滞现象与非线性项存在的情况,上述的研究并没有考虑.另外上述的文献只研究了切换系统的指数稳定性性能和H∞性能,本文研究了更一般的耗散性能.如果称一个系统为耗散系统,简单地说,是指这个系统从系统外部流入能量的速率不能低于系统内部存储能量的速率.也就是说,当没有外部能量供应时,存储在耗散系统中的能量将会消失.近年来,耗散性理论已经成为研究非线性系统稳定性分析和控制器设计的有效方法.该理论广泛应用于各类系统的控制器设计,例如文献[13]考虑了带有时滞项的离散时间切换线性系统的无源性与稳定性.文献[14]运用无源性理论研究了切换非线性系统的渐近稳定性.然而有关带有不稳定子系统和混合时滞的的切换系统的无源性或耗散性和指数镇定问题迄今尚未得到研究.
本文利用耗散性理论和模态依赖平均驻留时间方法研究了带有混合时滞的切换系统的耗散性和全局指数镇定问题.与已有的研究成果相比,本文的主要贡献如下:
1) 研究了一类具有混合时变时滞的更一般的系统模型,同时考虑了不稳定子系统存在的情况,使得到的结果在实际运用中更具有一般性,并把子系统全部是稳定的情况作为一个特例;
2) 针对带有不稳定子系统的非线性切换时滞系统,设计了一种由慢切换和快切换组成的具有高效模态依赖平均驻留时间的切换规则,建立了一组时滞相关的可行条件,使系统达到严格的〈Q,S,R〉-γ耗散性和全局指数稳定性;
3) 利用较少保守性的多Lyapunov-Krasovskii泛函方法和Jensen不等式技术,得到了一组由LMI工具箱可解的可镇定的反馈耗散控制器条件.
2 问题描述与预备知识
2.1 问题描述
考虑如下所示的带有混合时滞的切换系统:

定义1如果存在标量γ >0,对于T >0,在任意零初始条件下,满足
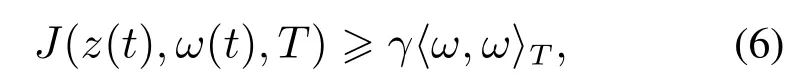
则系统(5)是〈Q,S,R〉-γ严格耗散的,并且γ称为耗散性能的边界值.
注1耗散性通过调整权重矩阵,有以下性能成立:
1) H∞性能:Q=-I,S=0,R=2γI;
2) 无源性:Q=0,S=I,R=0.
本文的控制目的:对具有不稳定子系统和混合时滞的非线性切换系统(1),能够在任意的初始条件下,设计严格的状态反馈耗散控制器(4)使得:
1) 闭环系统(5)在外部干扰ω(t)=0时实现全局指数稳定性;
2) 对于给定的γ >0,非零外部干扰ω(t)与控制输出满足定义1中的严格耗散性能(6).
2.2 预备知识
定义2如果存在常数k≥1,α >0,使得对于任意初始时刻,当u(t)=0,ω(t)=0时,解x(t)满足

则称τap是切换信号σ(t)的快切换模态依赖平均驻留时间.
3 稳定性分析与耗散控制设计
3.1 稳定性与耗散性分析
定理1对于给定标量,p=0,1,2,···满足如下条件:
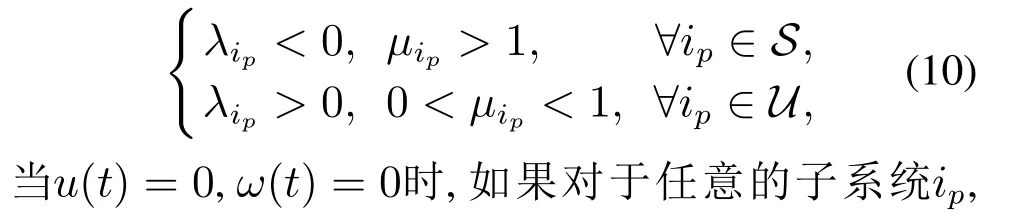

其中S表示稳定子系统的集合,U表示不稳定子系统的集合.那么系统(1)是全局指数稳定的.
证对于任何t≥t0,t ∈[tk,tk+1),对 式(13)的两边从tk到t积分有

注2定理1考虑了带有混合时滞非线性切换系统的全局指数稳定问题.为了解决不稳定子系统存在的情况,本文设计了一个基于模态依赖平均驻留时间的快切换与慢切换的组合切换信号,使得到的结果比一些存在的结果更一般[10-11].式(14)表明当稳定子系统处于激活状态时,其运行的时间不能小于相应的模态依赖平均驻留时间,即要进行慢切换;当不稳定子系统处于激活状态时,其运行时间不能大于相应的模态依赖平均驻留时间,即要进行快切换.式(15)表明了在稳定子系统上系统能量是递减的而在不稳定子系统上能量是递增的.

那么对于任意满足式(14)的切换信号,u(t)=0时系统(1)是严格〈Q,S,R〉-γ耗散的,且在ω(t)=0情况下满足全局指数稳定.
证对于任意的t ∈[tk,tk+1),σ(t)=ik,构造如下Lyapunov-Krasovskii泛函:
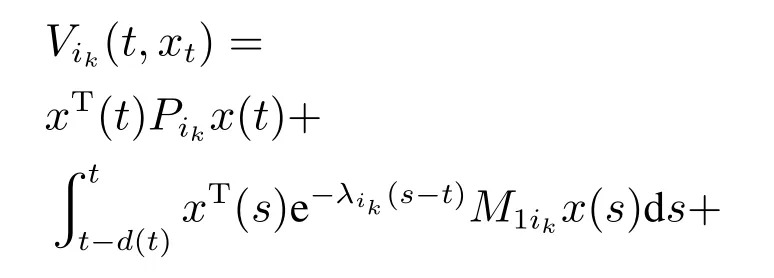


因此,根据定义1,可知非线性切换系统(1)是严格〈Q,S,R〉-γ耗散的.
接下来,考虑当ω(t)=0,u(t)=0时,非线性切换系统(1)的指数稳定性性能.把ω(t)=0代入式(24),有

结合条件(19)-(20),再根据定理1可知非线性切换系统(1)是全局指数稳定的. 证毕.
注3定理2基于Lyapunov-Krasovskii泛函方法对系统(1)进行了稳定性与耗散性分析.利用耗散性理论抑制外部扰动的影响,提出了保证系统严格〈Q,S,R〉-γ耗散性与全局指数稳定的充分条件.值得指出的是根据矩阵不等式的性质,满足式(18)的必要条件是对角线矩阵是负定的,因此本文假设时变时滞函数满足式(2).
3.2 控制器设计
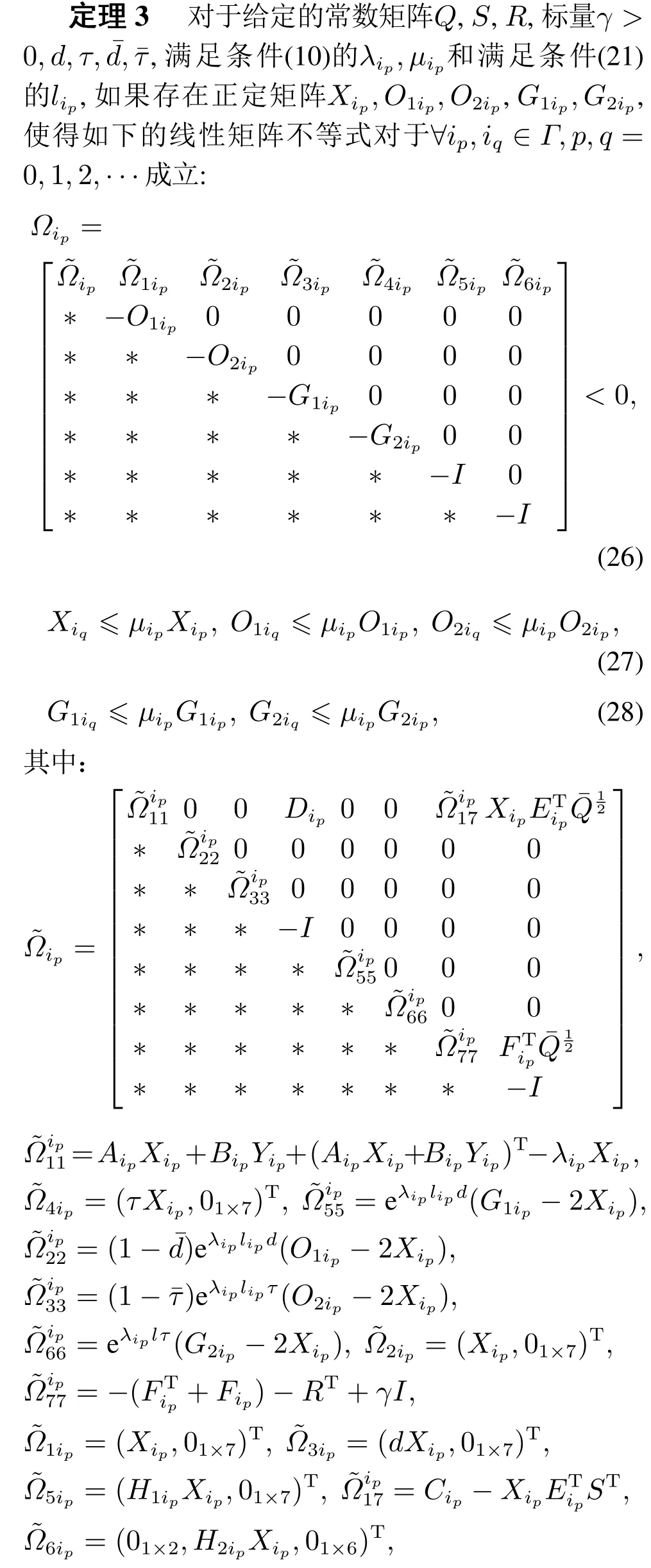
那么闭环系统(5)在任意满足条件(14)的切换信号下是全局指数稳定的,同时也是严格〈Q,S,R〉-γ耗散的.进一步,控制器增益矩阵可表示为如下形式:
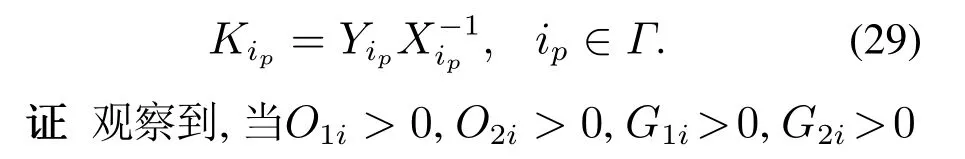

进一步应用Schur补引理可得条件(18),再根据条件(27)可知定理1的条件满足. 证毕.
4 数值仿真
把非线性切换系统(1)对切换神经网络系统进行建模.假设该神经网络系统有两种运行模态,每个子神经网络包含两个神经元.其中两种模态的参数如下:

对应的非线性项,外部干扰,和时变时滞项取值如下:
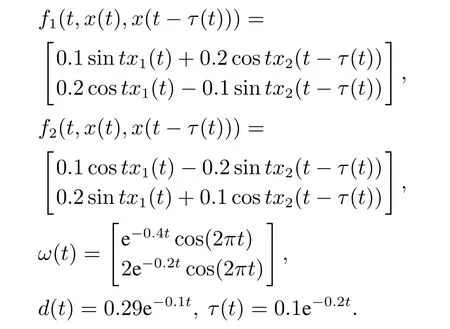
接下来的目标是协同设计一组状态反馈控制器和一组依赖于模态依赖平均驻留时间的切换信号,使得由上面参数构成的的非线性切换系统不仅是全局指数稳定性的而且满足严格的(Q,S,R)-γ耗散性能.令Q=-0.01I,S=I,R=0.1I,γ=0.2,λ1=-3.8,μ1=11,λ2=5,μ2=0.1,l1=1,l2=0,解定理3可得

选取初始状态x(0)=[1-1]T,图1和图2分别展示了模态1和模态2在设计的控制器下的状态轨迹,从图中显然可知此时模态1是稳定的而模态2是不稳定的.目前已有的结果还不能解决这类带有不稳定子系统和混合时变时滞项的切换系统的耗散性问题.本文设计的慢切换和快切换相结合的模态依赖平均驻留时间方法考虑了不稳定子系统存在的情况.根据切换规则(15)可解得τa1≥0.6310和τa2≤0.4605.如图3所示,选择满足模态依赖驻留时间的切换信号,此时闭环系统的状态轨迹是收敛到零的.进一步,图4中的函数值都大于零,这表示定义1中的式(6)成立,即闭环系统是满足严格耗散性的.因此,本文所提出的方法是有效的.
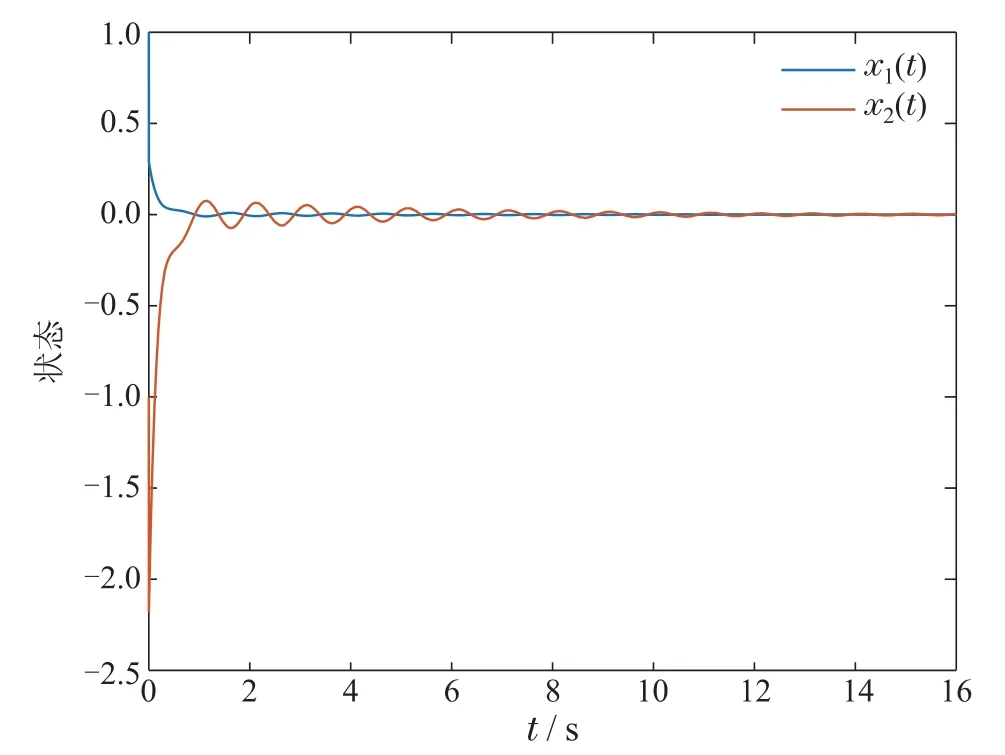
图1 模态1的状态轨迹Fig.1 State trajectory of mode 1
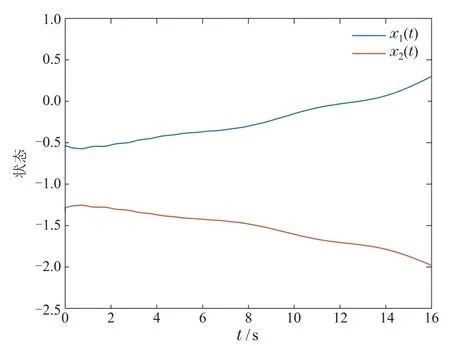
图2 模态2的状态轨迹Fig.2 State trajectory of mode 2
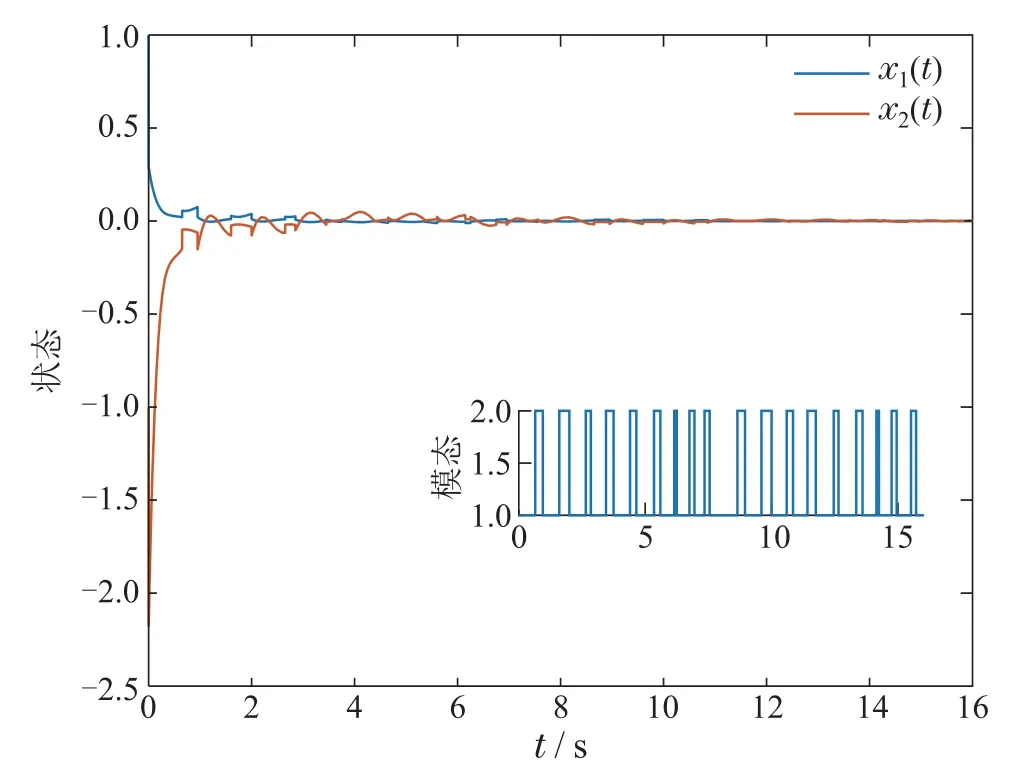
图3 闭环系统的切换信号与状态轨迹Fig.3 Switching signal σ(t) and state trajectory of the closed-loop system
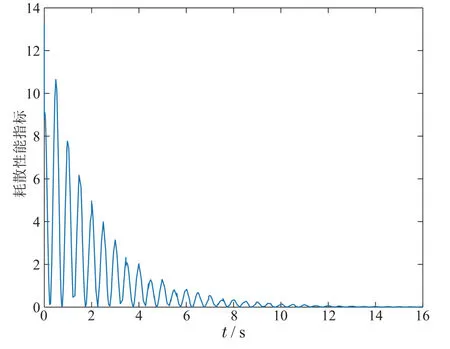
图4 耗散性能指标函数:-Λ(t)=zT(t)Qz(t)+2zTSω(t)+ωT(t)(R-γI)ω(t)Fig.4 Dissipative performance index function:-Λ(t)=zT(t)Qz(t)+2zTSω(t)+ωT(t)(R-γI)ω(t)
5 结论
本文研究了具有不稳定子系统和混合时滞的切换系统的耗散性分析与控制问题.利用模态依赖平均驻留时间技术、多重Lyapunov-Krasovskii 泛函方法和Jensen不等式,得到了保证闭环系统具有指数稳定和耗散性质的时滞相关的充分条件.分别针对不稳定子系统和稳定子系统,设计了由模态依赖平均驻留时间的快切换和慢切换组合成的新切换信号.进一步,通过Schur补引理和矩阵变换方法得到一组可解的LMI条件.最后给出一个数值例子去证明本文所提出方法的有效性.

