基于Welch 法的协方差随机子空间方法的模态参数识别1)

李雪艳 官宇航 罗铭涛 吴博宇

(暨南大学力学与建筑工程学院,重大工程灾害与控制教育部重点实验室,广州 510632)

引言

环境激励下的模态参数分析[1-3]是在风荷载、车辆荷载、地震和冲击荷载的作用下,对仅有输出(响应)的工程结构进行模态参数识别的一类结构动力学反问题.相较于传统的模态参数识别方法,这种方法无需测定未知的激励,不影响结构的正常运行,不仅费用低,而且可以识别出结构正常运行时的模态,因而该类方法具有广阔的应用前景[4].

随机子空间法(stochastic subspace method,SSI)[5-8]作为一种适用于环境激励下的模态参数识别的时域识别方法,基于系统的离散时间状态空间模型,并假定环境激励为平稳白噪声,再经过矩阵QR 分解或者奇异值分解之后得到系统状态矩阵,再利用特征值和特征向量计算出频率、振型和阻尼比等模态参数[9].由于系统的真实阶次难以确定,Peeters等[10]提出稳定图法来确定系统阶次,以此来识别出更加真实准确的模态.随机子空间法可以分为协方差驱动随机子空间法[11-12]和数据驱动随机子空间法[13-14],前者需要由Hankel 矩阵计算输出响应的协方差矩阵,再经过奇异值分解得到系统矩阵,后者由Hankel 矩阵得到将来行空间投影到过去行空间的投影矩阵,再进行卡尔曼滤波和QR 分解来求解出系统矩阵,避免了协方差的计算.然而,实际工程结构受到的环境激励是较为复杂的,因此把环境激励假定为平稳白噪声可能会使得识别结果中出现虚假模态或者真实频率出现误差[15].

为了改进随机子空间法,目前已有许多尝试.秦世强等[16]利用大桥频率低、模态密集等特点,提出引入屏蔽信号限制经验模态分解(EMD)过程中的带宽以消除模态混叠.Lu 等[17]提出了一种能实现非同步数据的模态参数识别随机子空间法,该方法的核心是使用模态的平均相位偏移(mean phase deviation,MPD)来找出实际的时滞以及同时计算实际振型分量.Lin 等[18]把协方差驱动随机子空间法(COV-SSI)和数据驱动随机子空间法(DATA-SSI)相结合,通过对改进投影矩阵进行奇异值分解,避免使用原始大维数据矩阵,来求解系统矩阵,可以有效提高随机子空间法的计算效率.陈永高等[19]尝试采用滑动窗口和相似度来确定系统的真实阶次,引入改进集成经验模式分解算法消除噪声影响,剔除虚假模态并避免模态遗漏.周筱航等[20]使用滑窗技术改进随机子空间法.Jin 等[21]提出一种短时随机子空间识别(ST-SSI)框架,通过分析驶过桥梁的车辆的动态响应来识别具有时变性的车桥耦合系统的频率.张永祥等[22]构建了一种基于谱系聚类的随机子空间模态参数自动识别算法,其基本原理是将模式样本按距离准则逐步聚类.Wen 等[23]提出了一种基于滑动窗口模糊C 均值聚类算法和确定性随机子空间辨识(SC-CDSI)相结合的时域识别方法,实现非线性时变结构模态参数的在线跟踪和识别.首先,对非线性时变结构的输入输出信号进行加窗分割;其次,为了满足稳定图中有效模态的自动识别,以模糊C 均值聚类算法(fuzzy C-means clustering analysis,FCM) 为基础,以频率、阻尼比和振型为聚类元素,实现了有效模态的自动智能选择.

尽管通过信号预处理、加窗函数、奇异值截断法和聚类分析等技术的引入,能部分改善随机子空间法的效果,但是随机子空间法在实际应用中仍然存在模态遗漏、虚假模态、计算量大和自动定阶困难等问题.实际工程结构承受着多样的环境激励,随机子空间法要准确地识别出模态参数,则需要较长时间段的输入数据,但这样会导致计算效率低下.所以本论文提出使用Welch 方法[24]和Hanning 窗,对信号在频域进行去除激励和噪声影响的处理,然后生成包含结构更多固有模态和较少激励频率的Toeplitz矩阵,再进行特征值分析,并使用模糊C 均值聚类算法[25-26]和模态平均相位偏移(MPD)[27-28]指标来识别结构的模态参数.并把本文所提出的方法应用于一座大跨悬索桥的实测加速度响应和一座高层建筑结构的实测加速度响应数据分析和模态参数识别,演示了所提方法的可行性和有效性.

1 基于Welch 法的协方差驱动随机子空间方法

1.1 识别状态矩阵

假设yk=是结构的m个测点的tk时刻的加速度响应,由t0到t2i+j-2时刻的加速度响应构造如下Hankel 矩阵

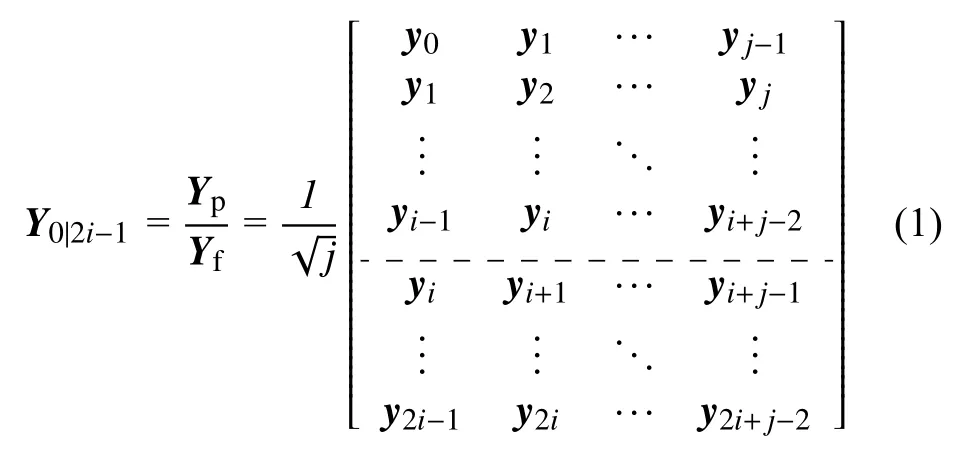
把矩阵分为两部分,“过去”和“将来”输出数据分别为Yp∈Ri×j和Yf∈Ri×j,由Hankel 矩阵可以得到Toeplitz 矩阵

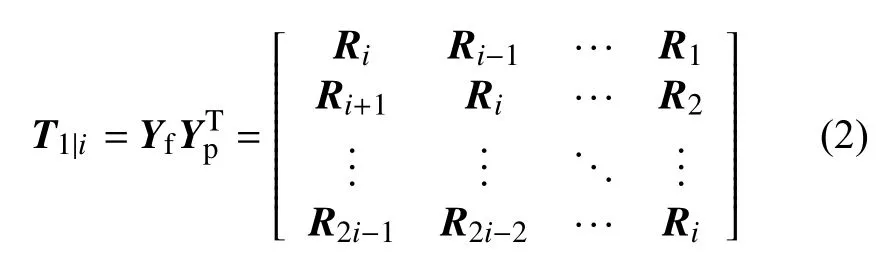
其中

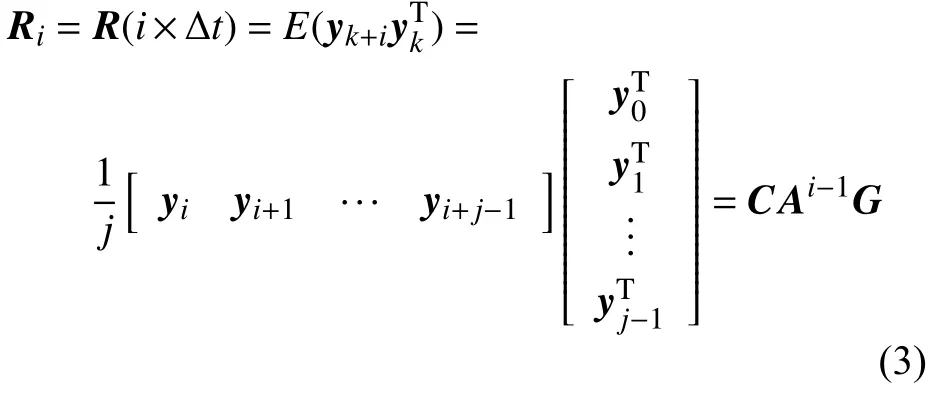
式中,C为跟测量位置有关的矩阵,A为离散状态矩阵,包含了结构的状态信息,如频率、振型和阻尼等参数,G为状态-输出协方差矩阵,i和j为数据长度,由于j为有限数,所以导致式(3)的左边不能严格等于右边,使得结构固有频率不能从众多激励和噪声频率中突显出来,为后续的子空间识别带来虚假频率.

而结构健康监测系统测试的加速度响应信号具有连续不间断和数据海量的特点,另一方面环境不确定因素多和激励复杂,激励数据未知.为了消除这些不利因素,可把时域的海量加速度响应信号通过加窗函数和傅里叶变换到频域进行平均计算.

式中,ω 是圆频率变量,j*是复数符号,Mr1,Cr1,Kr1分别为第r1阶模态质量,模态阻尼和模态刚度,F(ω)是激励力向量的傅里叶变换,Φl1r1是第r1阶振型Φr1的第l1个分量,N为结构的总自由度数.实际运营结构,如桥梁承受着多种激励,例如车流、风和地脉动等,但是这些外部激励具有随机性和不确定性,所以F(ω)具有随机性,而结构的固有频率不受外部环境影响,对事先给定时间长度的加速度响应信号的l段功率谱进行平均,可以降低激励频率的功率,而结构固有频率的功率将更突出,成为功率谱曲线上的少数极值点.再对进行逆傅里叶变换得到互相关函数

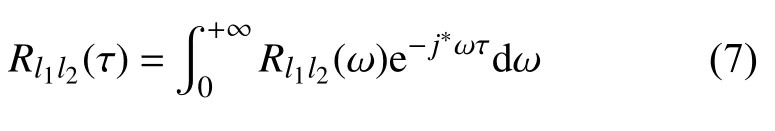
并把式(7)代入式(2)中则可以提高Toeplitz 矩阵的精度.

把式(3)代进Toeplitz 矩阵,则有

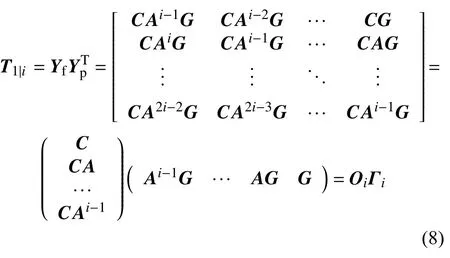
其中,Oi为可观矩阵,Γi为可控反转矩阵,再对由式(7)的相关函数构造的Toeplitz 矩阵进行奇异值分解

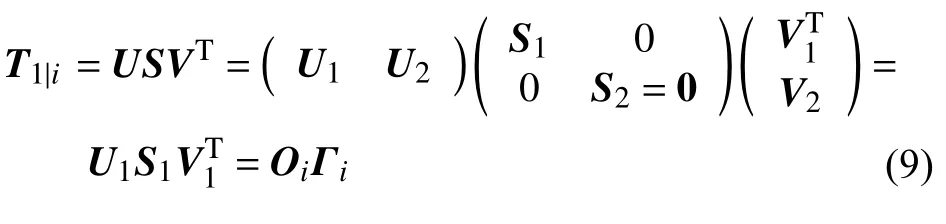
其中,U和V是正交矩阵,S是奇异值对角矩阵,S1和S2分别为非零奇异值和零奇异值对角矩阵,则有

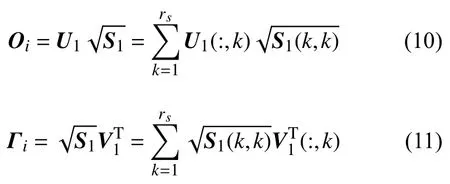
式中rs为非零奇异值的个数.

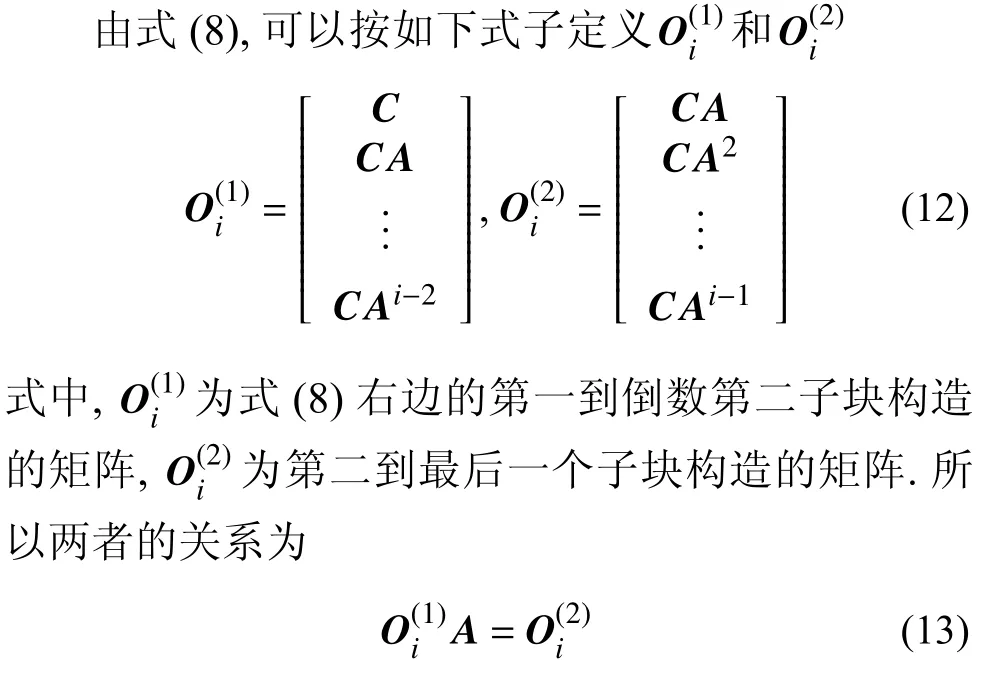
离散状态矩阵A可由下式求得

其中 (*)+表示广义逆.

1.2 频率识别

由离散状态矩阵A进行模态参数识别,对A进行特征值分解可得

1.3 模糊C 均值聚类(FCM)分析

其中,α 是加权指数,J(·) 为目标函数,uij和dij分别为xj对pi的隶属度和欧式距离.

引入 ρ=[ρ1,ρ2,···,]算子则有

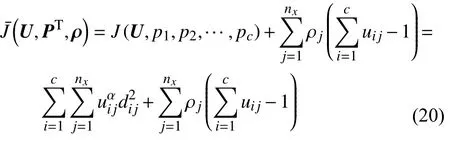
对所有输入参量求偏导可知式(20)取最小值的必要条件为

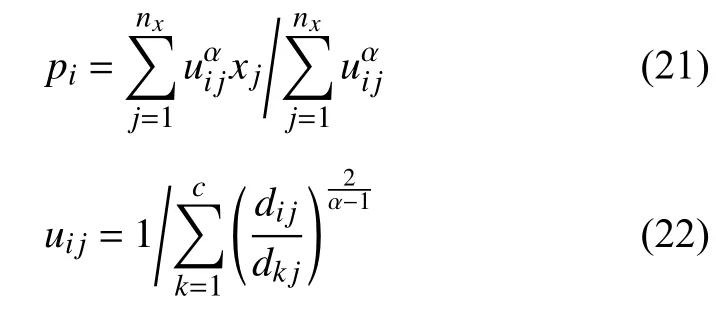
由离散状态矩阵A可以得到一组频率 [ω1,ω2,···,],通过变换式(10)中的r∈[rmin,rmax],可以得到多组[ω1,ω2,···,]r,把所有频率作为样本进行FCM 聚类分析.给定加权指数 α=2[29],选择最多的一组频率 [ω1,ω2,···,ωc] 作为初始聚类中心P,初始隶属度矩阵U按下式计算

1.4 平均相位偏移(MPD)定阶

当结构具有低阻尼和对称正定的刚度矩阵时,结构振型为实数振型,由式(18)得到的各阶振型的各个分量的相位角应当相同或者相近,所以其对相位平均值的偏移较少.或者说相应模态振型的相位分散程度较少.

设第i阶模态的平均相位为[30]

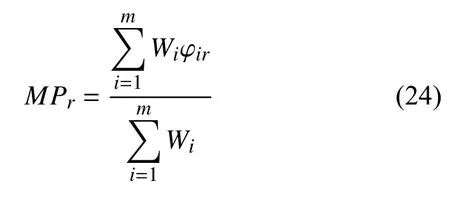
其中,φir为第r阶振型 Φr的第i个分量的相角,m为每一阶振型分量总数,也即测点数,Wi为每一阶振型分量的加权系数,可取1 或者 |Φir|,本文取后者即第r阶振型的第i分量的模.

第r阶振型第i分量的相角 φir按下式计算

式中,Re(·) 和 Im(·) 分别为变量的实部和虚部,若arctan(Re(Φir)/Im(Φir)) ≥0,φir原值不变,为负时后者加 π/2 .

各阶振型向量的平均相位偏移为

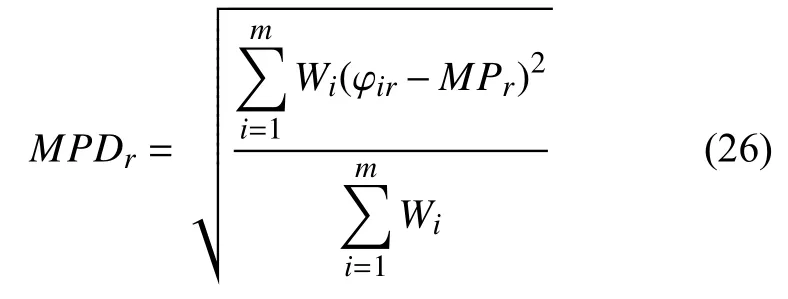
计算结果为偏移的弧度值,对于实模态,换算成角度值之后的MPDr计算结果应趋近于0,一般倘若MPD≥20°则认为相位偏移较大,对应的模态为虚假模态[30].

最后通过聚类的样本数和平均相位偏移来共同确定模态阶数.基于Welch 法,FCM 和MPD 分析的随机子空间法在模态参数识别时的流程图如图1 所示.

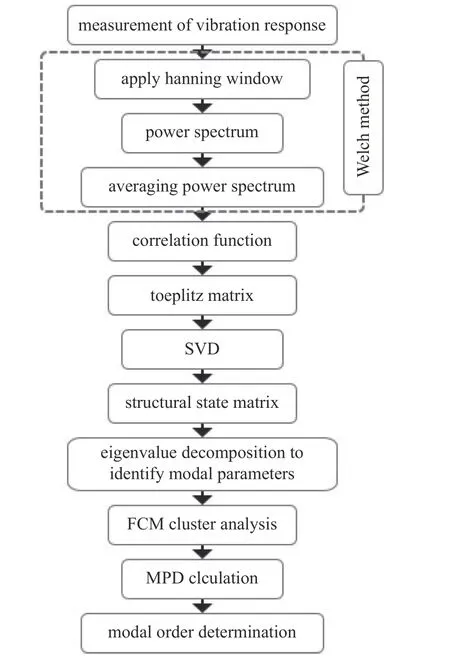
图1 基于Welch 法的随机子空间法的流程图Fig.1 Flow of stochastic subspace identification based on Welch method

2 实际工程结构模态参数识别

2.1 实桥模态分析

对位于广东省的一座大跨悬索桥的实测数据进行分析和演示本文所提出的方法.该桥的监测系统包括SLJ-100 力平衡加速度计、MSM-48 多通道数据采集器、信号电缆、GL-3 B 直流电以及用于控制和采集测量数据的计算机.加速度计的测量范围为 ± 2g,频率范围为0.0～80.0 Hz,灵敏度为1.25(V)/g,噪声小于0.5g.

以200 Hz 的采样频率采集加速度响应.传感器编号系统及其布置如图2 所示.包括3 个纵向(x方向) 加速度计(传感器8,32,20)、5 个横向(y方向)加速度计(传感器7,10,13,16,19)和8 个竖向(z方向)加速度计(传感器9,11,12,14,17,18,21).2020 年3 月2 日早上9 时录得的5 s 时间长度的加速度响应,如图3 所示.可以看到竖向加速度响应幅值明显大于纵向和横向的,说明主要是车辆载荷激振.

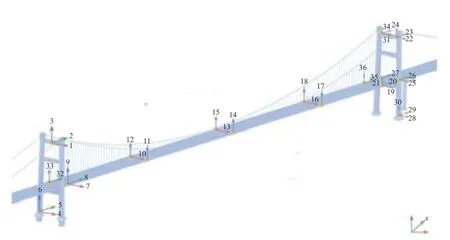
图2 悬索桥上加速度计的布置Fig.2 Arrangement of accelerometers on suspension bridge

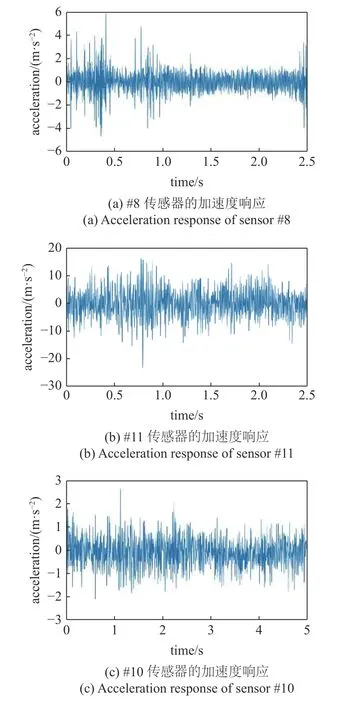
图3 悬索桥的加速度响应Fig.3 Acceleration response of suspension bridge

对桥板上13 个传感器(传感器8,32 和20;7,10,13 和19;9,11 和12,14 和15,17)的加速度响应数据进行分析和模态参数识别.首先对30 s 共6000 个数据点的加速度响应进行协方差驱动的随机子空间分析,得到的稳定图如图4(a)所示.对1 小时的加速度响应数据进行Welch 法加频域分解法(frequency-domain decomposition,FDD)[31],得到的功率谱曲线如图4(a)中所示的蓝线所示,文中后面图中的该曲线都为FDD 法计算得到.可以看出由传统SSI 法得到的稳定图中的优势频率较少,这主要是由于6000 个数据点长度的环境激励加速度响应数据在生成Hankel 矩阵和Toeplitz 矩阵时,无法有效消除环境激励等虚假频率.但是直接使用更长时间的加速度响应,会使得随机子空间法耗时更长,效率降低.

把1 小时长的各通道的加速度响应数据进行自相关分析,得到3000 数据点长度的相关函数数据代替加速度响应数据来生成Hankel 矩阵,并进而计算Toeplitz 矩阵和进行特征值分析,得到各个状态矩阵的频率,进行FCM 聚类分析,并使用MPD 进行模态参数的筛选确定,得到结果如图4(b)所示.可以看到已经能识别出13 个结构固有频率.之所以比图4(a)所示情况得以改善,是因为1 小时长度的自相关分析,显著降低了噪声和环境激励的影响,使得结构固有频率在相关函数中突显了出来,但是跟频域分解法的功率谱曲线相比,有模态遗漏现象.即第1,2,3,4,8 个峰值对应的频率都未能识别出来.

对1 小时长度的加速度响应数据,进行如式(4)～式(6)所给出的加窗和平均功率谱计算,对功率谱进行如式(7) 所给出的逆傅里叶变换,并直接构建Toeplitz 矩阵,然后进行状态矩阵计算和特征值分析,再进行FCM 聚类分析,聚类分析以后的稳定图如图4(c)中的红色部分所示,此时得到的类数目为241,远大于实际模态阶数,所以需要去除虚假模态.对每个类所对应的振型进行平均相位偏移(MPD)分析,即通过随机子空间法得到的每个复数振型的各个分量要具有相同或者相近的相位角,以使得实际振型为实数振型.对聚类分析以后各个类的振型进行MPD分析,得到如图5 所示的MPD分布图,对MPD＞ 20°所对应的类进行剔除,留下的模态对应的频率稳定图如图4(c)的蓝色竖线部分所示.可以看出第1,2,3 个峰值对应的频率都能识别出来,说明了基于Welch 法的随机子空间法在改善模态遗漏方面有显著提高.

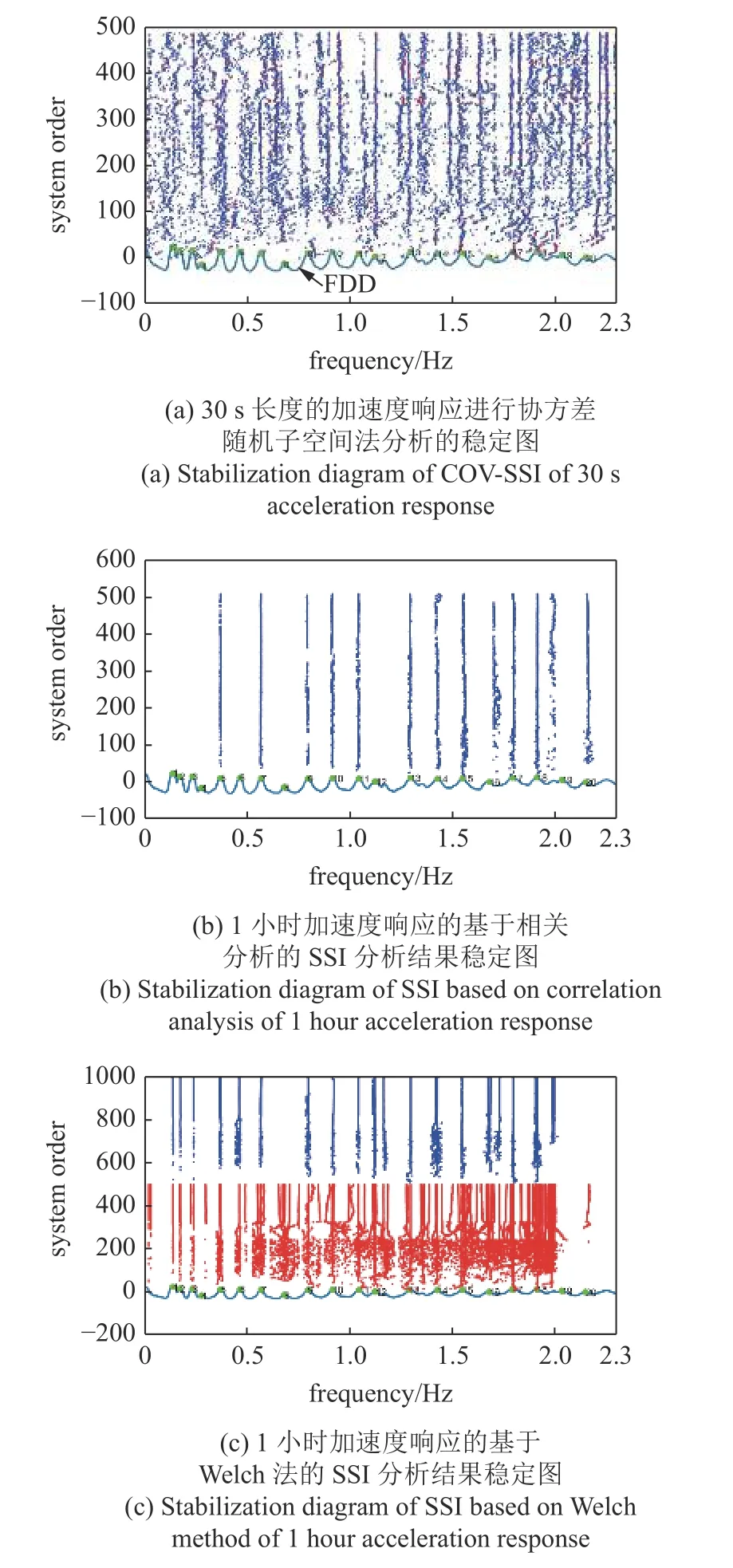
图4 频域分解法FDD、传统SSI、基于相关分析的SSI 和基于Welch 法的SSI 的某大跨悬索桥的频率识别Fig.4 Frequency identification of a long-span suspension bridge by FDD,traditional SSI,SSI based on correlation analysis and SSI based on Welch method

图5 对各聚类所对应的振型进行MPD分析得到的MPD分布图Fig.5 the distribution of MPDobtained by MPDanalysis of vibration modes corresponding to each cluster

在识别出结构的频率以后,再提取结构的振型,由于该实桥桥板上分三个方向仅安装了16 个传感器,且只有13 个传感器在该时段测得有效数据,所以只能识别得到部分振型分量.在图6 中显示了三个频率各自对应的振型分量,可以看到在相同截面和相同方向的振型分量有相近的值,符合理论结果.也跟用频域分解法识别得到的对应振型分量进行了比较,发现具有较好的匹配性,再一次证明了所提方法的正确性.

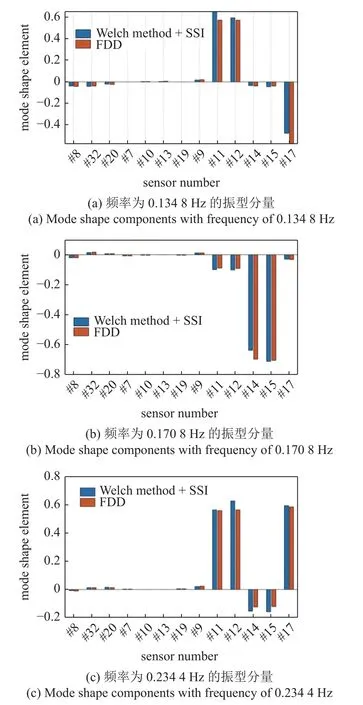
图6 使用基于Welch 法的SSI 和FDD 法得到的悬索桥的三阶振型分量对比Fig.6 Comparison of three orders mode shape components of suspension bridges obtained by using SSI based on Welch method and FDD

使用Welch 法+频域分解的峰值法、传统协方差随机子空间法、基于相关分析的随机子空间法和基于Welch 法的随机子空间法的识别结果如表1所示,可以看到基于Welch 法的随机子空间法,在FCM 和MPD 的协助下,在模态遗漏、虚假模态剔除和自动识别方面具有明显优势.

表1 大跨悬索桥的频率识别结果(Hz)Table 1 The identified frequency results of long-span suspension bridge (Hz)

2.2 环境激励下的高层建筑模态分析

第二个研究对象是如图7 所示的七十层高层建筑,在该建筑物的地下和第68 层安装了三方向加速度传感器,采用INV3062V 采集仪和91B 加速度传感器,采样频率为100 Hz.分析第68 层的3 个方向的加速度响应,该加速度响应如图8 所示.

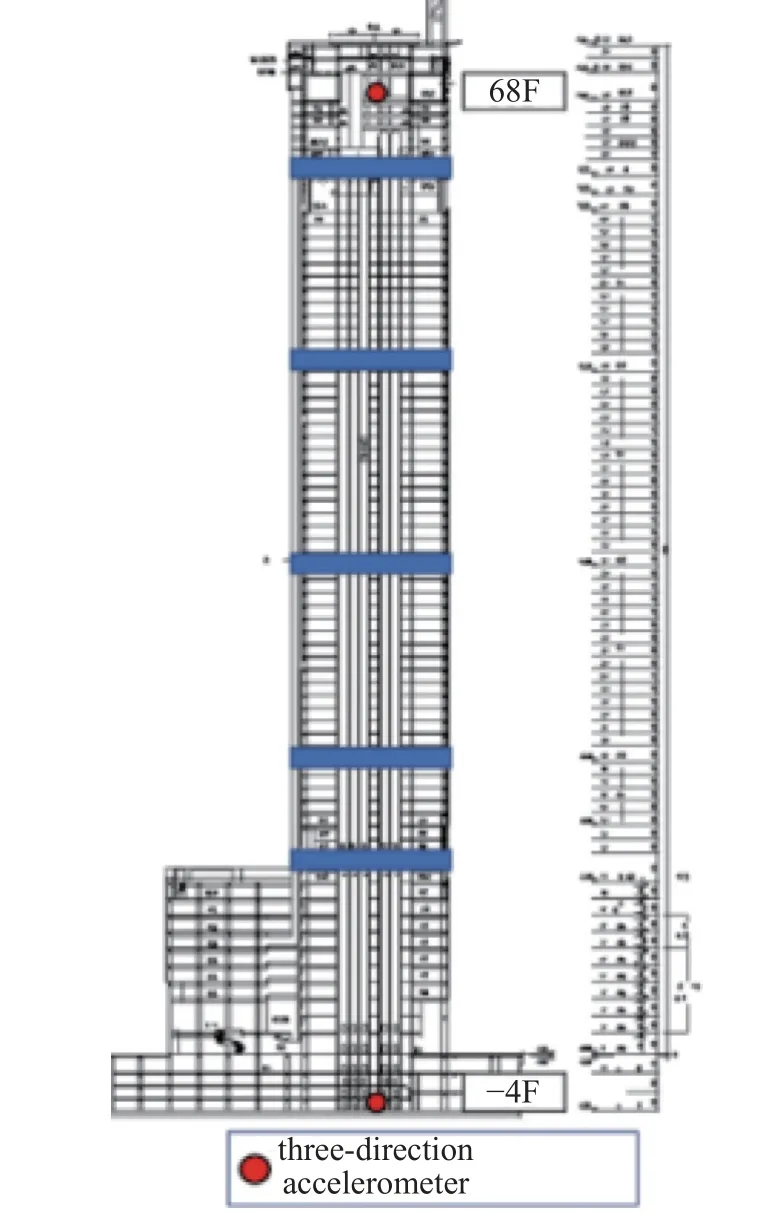
图7 某高层建筑的传感器布置图Fig.7 Sensor layout of a high-rise building

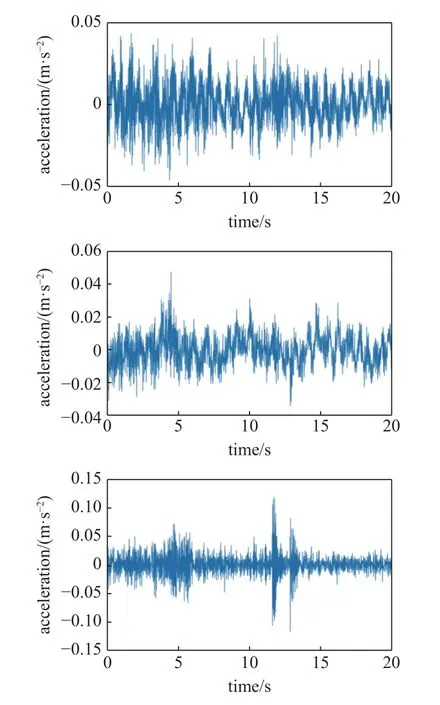
图8 某大厦的第68 层处测点的加速度响应Fig.8 Acceleration response of a certain measuring point in a high-rise building

首先使用20 s 共2000 个数据点长度的加速度响应,直接进行协方差驱动的随机子空间分析,如图9(a)所示,红色部分数据是传统SSI 分析的稳定图结果,蓝色部分数据是使用FCM 聚类分析和MPD筛选以后所确定的模态阶数,所计算结果也跟频域分解法的功率谱曲线进行了比较,可以看到模态遗漏问题非常严重,这是因为结构固有模态的振动能量跟环境激励频率的振动能量相比较小,在随机子空间法中不能成为主要特征值被识别出来.

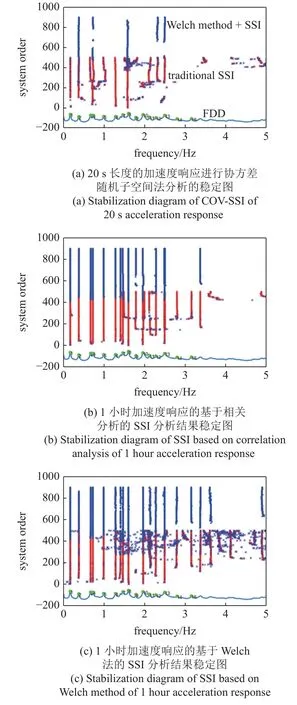
图9 某大厦的频率识别Fig.9 Frequency identification of a building

对1 小时的加速度响应进行自相关分析,取前3000 个数据点来形成Hankel 矩阵和Toeplitz 矩阵,最后的识别结果如图9(b)所示,同样蓝色部分为经过FCM 和MPD 分析后的模态阶数,相比于图9(a)的结果,模态阶数显著增加了,但是相对于频域分解法,仍然有模态遗漏的问题.

对1 小时的加速度响应使用本文中提出的Welch 法分析和直接形成Toeplitz 矩阵,最后的识别结果如图9(c)所示,可以看到在通过FCM 和MPD分析以后,模态阶数显著增加,跟频域分解法能识别出来的峰值基本对应,但是能避免频域分解法中的虚假峰值,从而识别出更准确的结构模态.

频域分解法、传统协方差SSI、基于相关分析的SSI 和基于Welch 法的SSI 识别的某高层大厦的模态频率如表2 所示,从表中看出基于Welch 法的SSI 法在避免模态遗漏,剔除虚假频率,自动识别方面具有显著优势.虽然频域分解法也能获得比较全面的结构模态,但是由于所有频率都会以峰值的形式呈现出来,所以虚假峰值问题也难以避免.

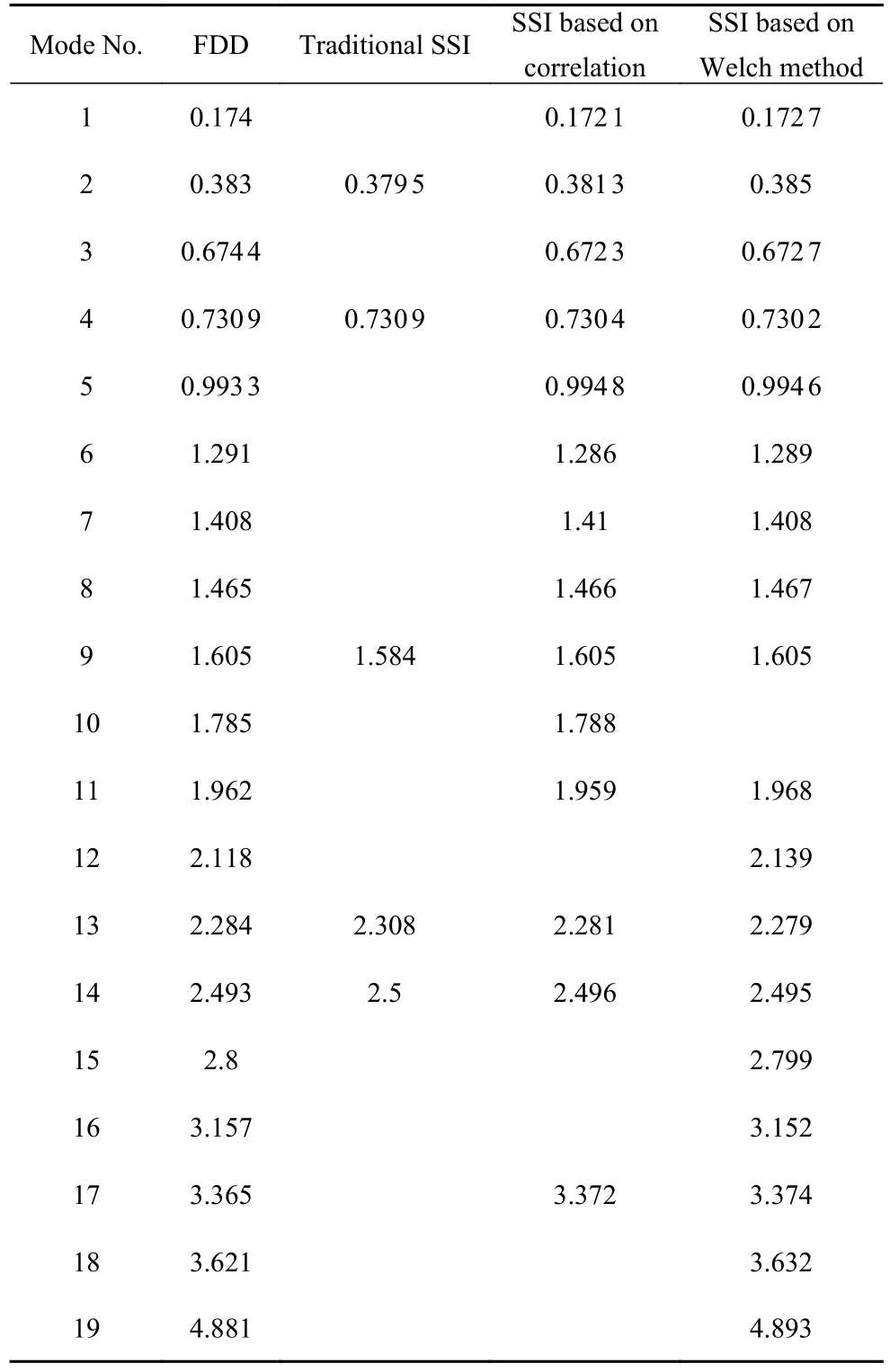
表2 某大厦的频率识别结果(Hz)Table 2 The identified frequency results of a building (Hz)

3 结论

由于环境激励复杂,并不完全符合平稳白噪声的特征,使得传统的随机子空间方法在计算效率、剔除虚假模态和避免模态遗漏方面存在不可忽视的问题,限制了该方法在实际工程结构的自动模态参数识别追踪方面的应用.因此尝试在频域对测试数据的模态频率振动能量进行加强,而对环境激励频率和噪声频率的振动能量进行降低,所以提出了基于Welch 方法的随机子空间法.由Welch 方法得到经过频域平均的振动响应协方差参数,并形成Topelitz 矩阵,然后进行奇异值分析,由不同阶数的奇异值构造的状态矩阵进行特征值分析,得到频率数据样本,然后进行模糊C 均值聚类分析,和模态的平均相位偏移分析,剔除MPD 值过大的虚假模态,对SSI 识别的模态进行定阶.通过对一座大跨悬索桥的桥板上的13 个加速度传感器的1 小时数据的分析,和一座高层大厦的3 个加速度传感器的1 小时数据分析,发现基于Welch 方法的SSI 相比于传统SSI 和基于相关分析的SSI,在避免模态遗漏和计算效率方面有显著提高,而相对于频域分解法则在自动识别和剔除虚假模态方面有明显优势.所以本文提出的基于Welch 方法的SSI,在环境激励下工程结构的模态参数识别追踪方面具有较好的应用前景.