翼反角对高压捕获翼构型亚声速气动特性影响分析研究1)
常思源 肖 尧,†,2) 李广利,† 田中伟 崔 凯,†
* (中国科学院力学研究所高温气体动力学国家重点实验室,北京 100190)
† (中国科学院大学工程科学学院,北京 100049)
** (中国科学院力学研究所宽域飞行工程科学与应用中心,北京 100190)
引言
随着航空航天技术的快速发展,人类在临近空间的探索与应用等活动日益频繁,飞行任务向多样化、复杂化及智能化等方向发展,高昂的飞行成本也逐渐成为一个十分突出的问题,各国对速域更宽、空域更广、航程更远、成本更低且重复性更强的高超声速飞行器的需求更加旺盛.
长久以来,欧、美、日等发达国家对宽速域高超声速飞行器开展了大量研究.2013 年,美国希德·马丁公司公布了SR-72 高超声速临近空间无人侦察机长期发展计划;欧共体先后资助2 次的LAPCAT 计划[1-2],旨在研发用于MR2 高超声速飞机[3]的长时高性能推进系统;2014 年起,欧洲、俄罗斯和澳大利亚联合开展了“高超声速飞行试验-国际合作(HEXAFLY-INT)”项目[4-5],其远景目标是发展一种能够2~3 h 从欧洲飞至亚洲或澳洲的高超声速客机.在学术界,以日本学者Lobbia 等[6-8]和意大利学者Aprovitola 等[9-10]为代表的团队分别针对高超声速再入飞行器开展了大量多学科优化设计研究;美国迈阿密大学查戈成等[11]和Espinal 等[12]提出了一种超声速“双向飞翼”概念,国内外对该新型布局向高超速域进行了一定程度的拓展[13-14].整体而言,关于宽速域高超声速飞行器的研究大多仍处于概念探索层面,距离真正的实际飞行还面临很多关键技术亟待攻关.
从当前的研究态势来看,大多数宽速域高超声速飞行器主要基于“乘波体”布局设计[15].然而,在高超声速条件下升阻比与容积率之间存在十分强烈的制约关系.例如,为了获得较高的升阻比以提升航程等指标,往往需要进行扁平化设计.因此,装载能力相对有限,容积率仍有待进一步提升.针对这一问题,崔凯等[16-17]提出了一种“高压捕获翼(high-pressure capturing wing,HCW)”新型气动布局概念,其基本原理是在机体上方合适的位置引入捕获翼,合理利用机体在高超声速条件下产生的激波,从而在捕获翼上形成有益气动干扰,能够保证飞行器在获得大容积率的同时,显著提高其升力和升阻比.
目前,针对HCW 新型气动布局的研究主要集中在高超声速条件下的外形优化设计[18-19]与气动性能评估[20-21].研究结果表明,该布局在高超声速条件下可以有效缓解升阻比、容积率与升力系数之间的矛盾关系,为未来高超声速飞行器气动布局设计提供了新的思路.此外,考虑到现有的宽速域高超声速飞行器大多采用大后掠、小展弦比的布局设计,其在低速飞行阶段,特别是起降阶段面临升力不足、稳定性差等缺陷,针对该问题,部分学者从变构型[22-23]、翼型设计[24-25]、前缘优化[26]等方面进行了探索研究.与传统布局方式相比,捕获翼的引入使得HCW 气动布局具有双升力面,有望改善低速条件下升力不足的问题.为此,王浩祥等[27-29]针对一种圆锥-圆台组合平板简化构型,对HCW 新型布局在亚/跨/超声速下的基本流场特性进行了初步研究,重点分析了机体与捕获翼之间的气动耦合效应.
然而,在HCW 新型气动布局的低速稳定性方面,相关研究尚处于起步阶段.一般来说,翼面上/下反是改变飞行器横航向稳定性的有效思路[30-32],特别在亚声速飞行器中十分常见.因此,对HCW 新型布局的翼面进行上/下反,综合改善其在亚声速条件下的气动性能和稳定性,是一项值得研究的课题.本文基于HCW 气动布局的基本原理,设计了一种概念构型,结合试验设计方法、数值模拟方法和代理模型方法,研究了基于翼面上/下反改善其亚声速稳定性的可行性,为HCW 气动布局在宽速域高超声速飞行器设计中提供了参考.
1 研究对象
1.1 高压捕获翼基本原理
高压捕获翼气动布局的基本设计原理如图1 所示,高速来流经过机体上壁面的剧烈压缩产生斜激波IS,在机体上方合适的位置安放一个薄翼(即高压捕获翼,下文简称捕获翼或HCW)用于“捕获”斜激波IS 并诱导出反射激波RS;这样来流在经过IS 和RS 两道激波的双重压缩后将在捕获翼下表面产生显著的高压区①;此外,由于捕获翼通常与来流近似平行,因此其上表面的压强相对较低.
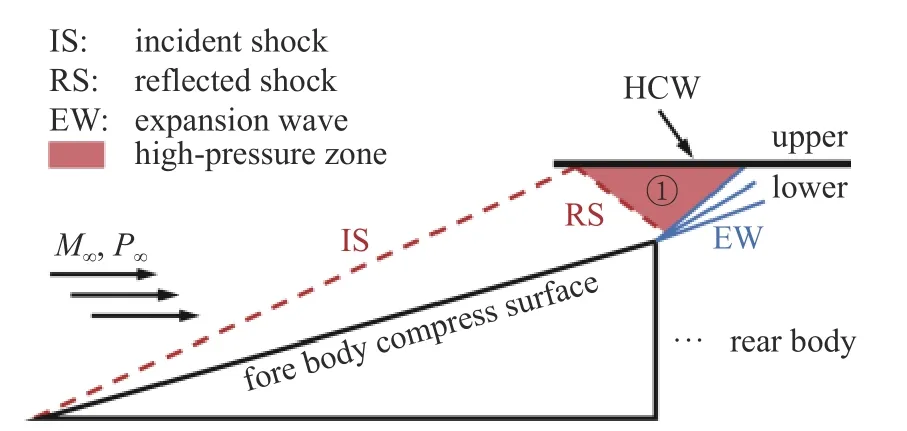
图1 高压捕获翼基本原理示意图Fig.1 Schematic diagram of HCW basic principle
一方面,捕获翼上/下表面存在较大的压强差,因此可为整机贡献较大的升力;另一方面,由于捕获翼通常采用薄翼设计,其阻力的增加有限,因此整机的升阻比也将显著提升.值得说明的是,通过合理设计机身型面,可以使反射激波RS 恰好掠过机身最高点,且气流经过机身最高点时会产生较强的膨胀波EW,进而显著削弱反射激波RS 的强度,能有效避免反射激波RS 对机体后段或捕获翼支撑结构产生不利的气动干扰.
1.2 高压捕获翼基准构型
根据上述HCW 基本原理,为了便于计算分析,本文设计了一种参数化概念构型,作为本文工作的基准构型.如图2 所示,基准构型包含捕获翼和机体三角翼(body delta wing,BW)两个升力面,捕获翼通过单立板支撑与机体后部相连,根据文献[18]中的准则可以确定捕获翼在机体上方的位置,为了简化外形,三角翼与机身腹部直接拼接,其中两翼面及支撑均简化为等厚度的平板(且前缘线均为直线,并采用圆弧钝化),未考虑控制舵面.基准构型的一些主要几何参数如下: 对于机体,其轴向长度为1 m,上/下表面压缩角分别为9°和6°;对于捕获翼,其轴向长0.49 m,展向长0.8 m,前缘和尾缘的后掠角分别为30°和20°,装配攻角为3.5°;三角翼后掠角为70°,且厚度和捕获翼一样均为2 mm.
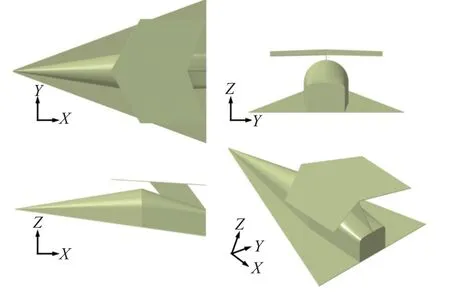
图2 高压捕获翼基准构型三维视图Fig.23 D view of the basic HCW configuration
进一步,对基准构型在设计状态点(马赫数Ma=6,高度H=30 km)下的流场开展了计算流体力学(computational fluid dynamics,CFD)数值仿真计算,飞行器物面及纵对称面上的压强分布如图3 所示,结果表明所给出的基准构型符合HCW 布局的基本设计原理,此处不再赘述.
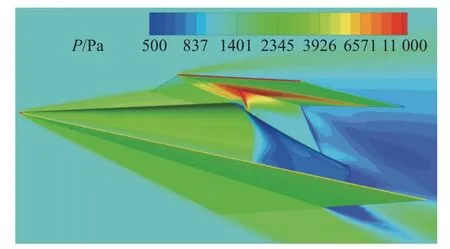
图3 基准构型压强云图Fig.3 Pressure contours of the basic configuration
1.3 含翼反角的高压捕获翼构型
从上述HCW 基准构型出发,在参数化建模中考虑两翼面的上/下反角,以研究翼反角对气动特性的影响.如图4 所示,分别从捕获翼和三角翼的翼尖处沿展向选取适当宽度的翼面进行上/下偏折.值得说明的是,由于偏折段宽度过小可能无法反映出翼反角对整机气动性能的影响,而受飞行器布局的限制偏折段宽度也不能过大,经综合考虑,捕获翼和三角翼偏折段的宽度分别取其对应半展长的0.5 倍和0.4 倍.此外,由于捕获翼和三角翼偏折段的形状分别为四边形和三角形,建模中上/下反的处理略有差异: 当捕获翼上/下反时,保证其展长不变;当三角翼上/下反时,保证其表面积不变.
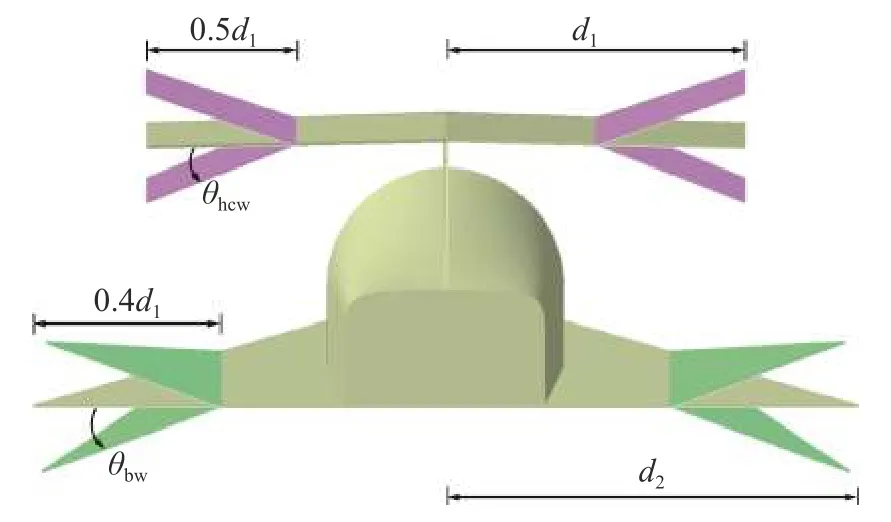
图4 翼面上/下反角示意图Fig.4 Schematic diagram of the wing dihedral/anhedral angles
为了便于描述,将捕获翼和机体三角翼的翼反角分别用 θhcw和 θbw表示,并规定正值表示上反,负值表示下反.表1 给定了两个设计变量的上/下界范围,即设计空间,其中三角翼反角的设计空间更大.当 θhcw=θbw=0°时,即对应基准构型.

表1 设计变量及取值范围Table 1 Design variables and space
2 分析方法
图5 给出了研究工作的分析流程.首先,基于所设计的HCW 基准构型,确定合适的设计变量及设计空间,选择均匀试验设计方法生成设计变量集,进而获得一系列含翼反角的HCW 构型作为构型样本集.然后,结合基准构型网格及批量网格生成脚本,完成所有样本构型计算网格的自动批量生成,对所有样本构型开展若干工况下的CFD 数值计算,并提取出相应的气动性能参数,构建气动数据集.最后,采用Kriging 代理模型方法分别对不同类别的气动数据进行建模,获取其在整个设计空间的响应,并结合典型外形的流场特性,分析翼反角对HCW 构型亚声速气动特性的影响.
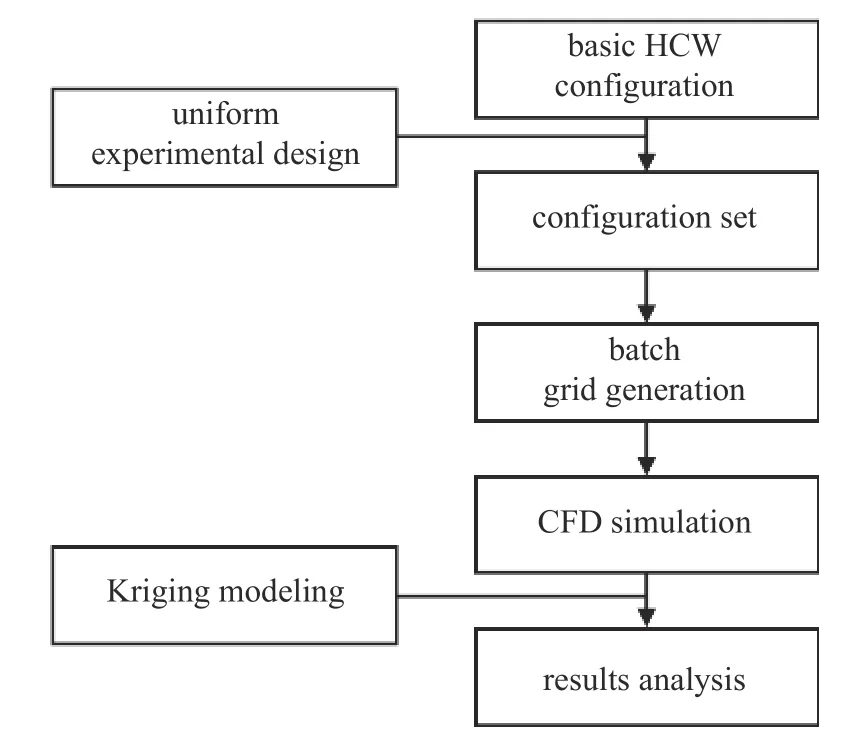
图5 分析流程图Fig.5 Flowchart of analysis
2.1 试验设计方法
为了构建高精度的输入-输出响应模型,往往需要使样本点在整个设计空间内均匀分散.采用了实际应用广泛的均匀试验设计(uniform design,UD)方法[33],使得构型样本均匀分布在整个设计空间.
在构建代理模型时,不仅需要训练样本集,往往还需要测试样本集用于考核代理模型的精度.对于训练样本集,为了充分覆盖表1 给出的设计空间,设定每个设计变量有81 个水平,采用UD 方法时每个水平仅使用一次,这样最终便获得了82 个训练样本点(包含基准构型),其分布如图6 中红色方形散点所示.进一步,采用UD 方法生成11 个样本点作为测试样本,其分布如图6 中绿色菱形散点所示.图7给出了测试样本集对应的11 个HCW 构型,可以看出,不同构型的外形差异明显,能有效代表不同水平的翼反角组合.

图6 试验设计样本点分布Fig.6 Experimental design sample point distribution
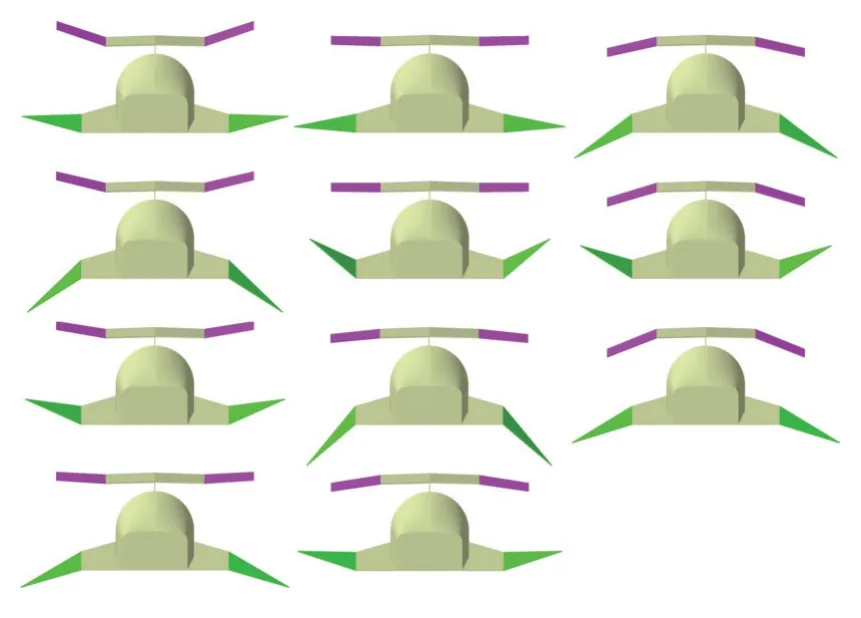
图7 构型的测试样本集Fig.7 Test sample set of configuration
2.2 数值模拟方法
本文基于CFD 数值模拟方法来评估不同构型的气动性能,首先需要划分流场的计算网格.为了获得高质量网格的同时兼顾生成效率,所有构型均采用混合网格,物面由三角形单元划分,通过向外层层拉伸生成三棱柱单元来刻画边界层流动;空间区域主要用六面体单元填充,局部由四面体单元和四棱锥单元进行过渡;远场边界为球面,球体中心位于飞行器顶点,半径为飞行器轴向长度的15 倍,以尽量缓解远场边界对亚声速计算的影响.图8 显示了翼反角 θhcw=20°,θbw=15°对应构型的计算网格,总网格单元数约为1091 万.

图8 计算网格Fig.8 Computational grid
本文所有构型的计算网格都是在基准构型网格的基础上,借助Python 脚本来实现批量自动生成的.首先,录制网格生成的宏文件,该宏文件可以依次实现网格生成软件的调用、基准构型网格的导入、捕获翼/三角翼翼尖处面网格的重建、体网格的生成、边界条件的设置及网格文件的输出等关键步骤.然后,编写Python 脚本,对宏文件中翼反角参数控制、文件输出路径等对应的命令行进行修改,从而得到新的宏文件.最后,按照给定的翼反角参数组合,反复进行宏文件的修改、保存和运行,便可以自动完成所有网格的生成.通过这种方式,不仅可以大大节省琐碎繁复的人工操作,提高网格生成效率,同时也能保证所有构型的网格质量及单元数基本一致.
在CFD 数值算法方面,采用有限体积法求解三维可压缩Navier-Stokes 方程,空间离散采用二阶精度、多维TVD 格式,时间推进采用二阶精度的双时间步方法,黏性通量采用二阶中心格式计算,并采用工程上应用广泛的二方程k-ε 湍流模型.该CFD 数值模拟方法的可靠性验证可以参阅文献[28-29],因为篇幅有限,本文不再赘述.
对每个构型,CFD 数值模拟的计算条件如下: 马赫数Ma=0.4,高度H=0 km;来流攻角 α 取0°,5°,10°,来流侧滑角 β 取0°,5°,其中侧滑角为正表示来流吹向右翼,即每个构型对应计算6 个工况;参考面积均取飞行器俯视投影面积,即0.368 m2,参考长度取机体轴向长度,即1 m,原点位于机体头部顶点,质心坐标均为(0.6,0,0) m.
2.3 代理模型方法
通过整理数值模拟结果,获取气动数据集,进而可以采用代理模型来构建设计变量与目标气动参数之间的映射关系.目前常用的代理模型主要有克里金(Kriging)模型、径向基函数模型及神经网络模型等,其中Kriging 模型已被广泛证明在求解强非线性问题中往往能够取得较好的拟合效果.因此采用实际中应用广泛的普通克里金(ordinary Kriging,OK)模型来进行建模,其表达式可以简单表示为


同时也要满足无偏约束条件

对于不同的目标参数,基于前述82 个训练样本构建相应的OK 模型,并用11 个测试样本来度量其模型精度.具体地,以前述2 个设计变量(经minmax 归一化后)为输入量,模型的输出量为单独某种气动性能参数,即每个目标参数对应一个OK 模型.
3 精度考核
3.1 网格无关性验证
网格无关性是校核CFD 数值模拟结果有效性的重要指标.本文以翼反角 θhcw=20°,θbw=15°对应的构型为例,分别生成了粗(coarse)、中(medium)和细(refined) 3 套网格开展网格无关性分析,网格单元总量依次约为551 万、1091 万和2109 万,壁面第一层网格厚度分别为 1.0×10-4m,5.0× 10-5m,2.0×10-5m,对应的Y+分别为35.0,16.7,6.6.
首先考察了气动力和力矩的计算结果.表2 给出了在攻角 α=10°、侧滑角 β=0°时升力系数CL、阻力系数CD及俯仰力矩系数Cm的计算结果,以细网格结果为基准,可以看出中网格与细网格之间的差异较小,均在0.95%以内;而粗网格与细网格之间的差异稍大,最大差异为俯仰力矩系数变化4.08%.
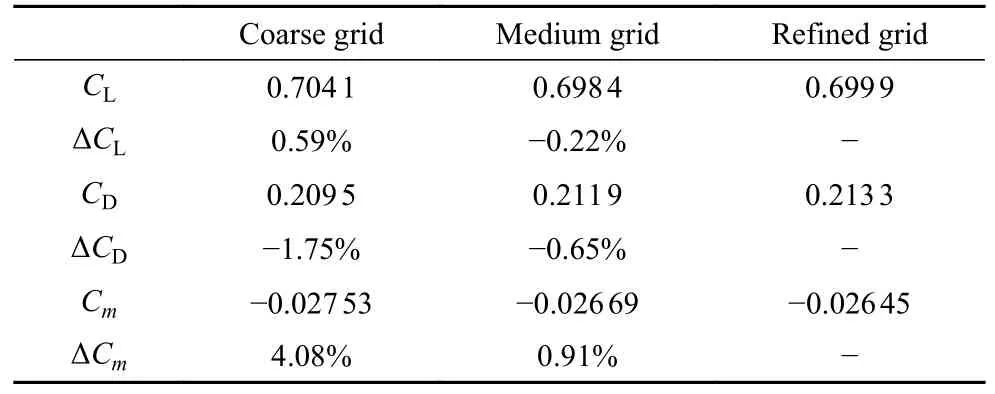
表2 不同网格下的气动力、力矩结果Table 2 Force and moment results of different grids
随后考察了攻角 α=0°时焦点位置Xac、横向静稳定导数Clβ及航向静稳定导数Cnβ的计算结果,如表3 所示,同样可以看到,中网格与细网格之间的差异较小,最大差异为Cnβ变化0.98%;而粗网格与细网格之间的差异十分明显,最大差异为Cnβ变化12.02%;相比之下,3 种网格计算出的Xac和Clβ都比较接近,均在1.5%以内.
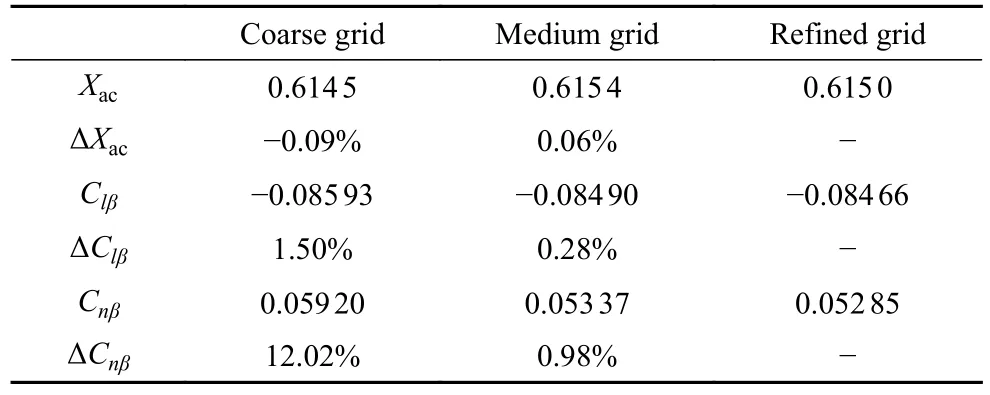
表3 不同网格下的稳定性参数结果Table 3 Stability parameter results of different grids
整体来看,中网格与细网格对应的升阻特性及稳定性参数相对误差在1%以内,而粗网格的航向静稳定导数及俯仰力矩误差较大.因此认为基于中网格,即网格量1100 万左右,获得的气动数据是可信的.
3.2 建模精度分析
为了度量不同目标参数OK 模型的精度,本文使用平均绝对误差(mean absolute error,MAE)和平均相对误差(mean relative error,MRE)两种指标来度量11 组测试样本数据的预测误差,从而说明不同目标参数的建模精度.
表4 给出了5 个主要的目标参数在不同攻角状态下的两种测试误差.可以看出,在所有攻角状态下,升阻特性参数CL和CD以及焦点位置Xac的建模精度较高,MRE 均在0.45%以内;而横航向静稳定导数Clβ和Cnβ的建模精度相对稍低,MRE 在0.75%~2.96%之间.虽然可以通过扩充训练样本来进一步提高Clβ和Cnβ的建模精度,但考虑到本文主要关心气动特性的变化规律,对其量值大小没有过高要求,因此可以适当放宽对建模精度的要求,即认为当前的建模精度足以支撑本文的分析.
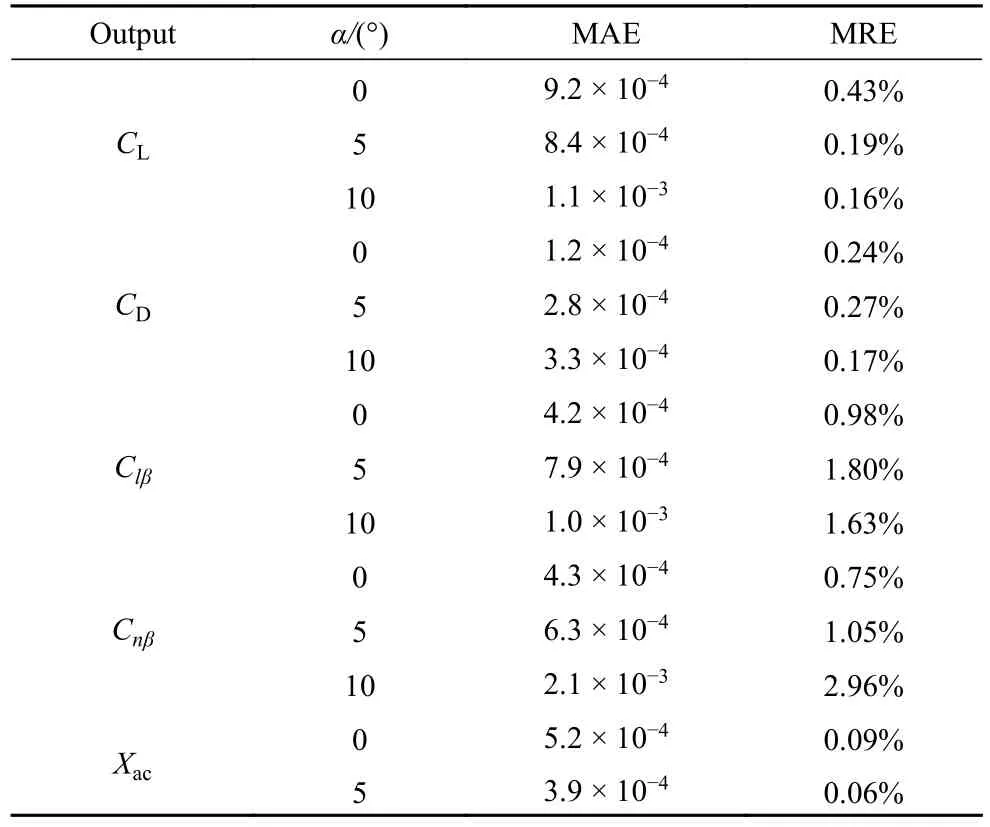
表4 不同目标参数的测试集误差Table 4 Test set errors for different target parameters
4 亚声速气动特性
4.1 升阻特性分析
首先分析翼反角对HCW 构型升阻特性的影响.图9(a)~ 图9(f)分别给出了攻角 α=0°,10°时升力系数CL、阻力系数CD和升阻比L/D在整个设计空间下的分布,其中横、纵坐标分别表示捕获翼和三角翼的反角;等值线表示相对于基准构型计算结果的变化率,且正值对应的等值线为实线,负值对应虚线.
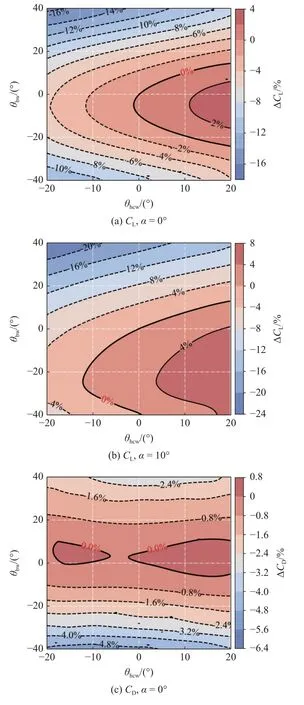
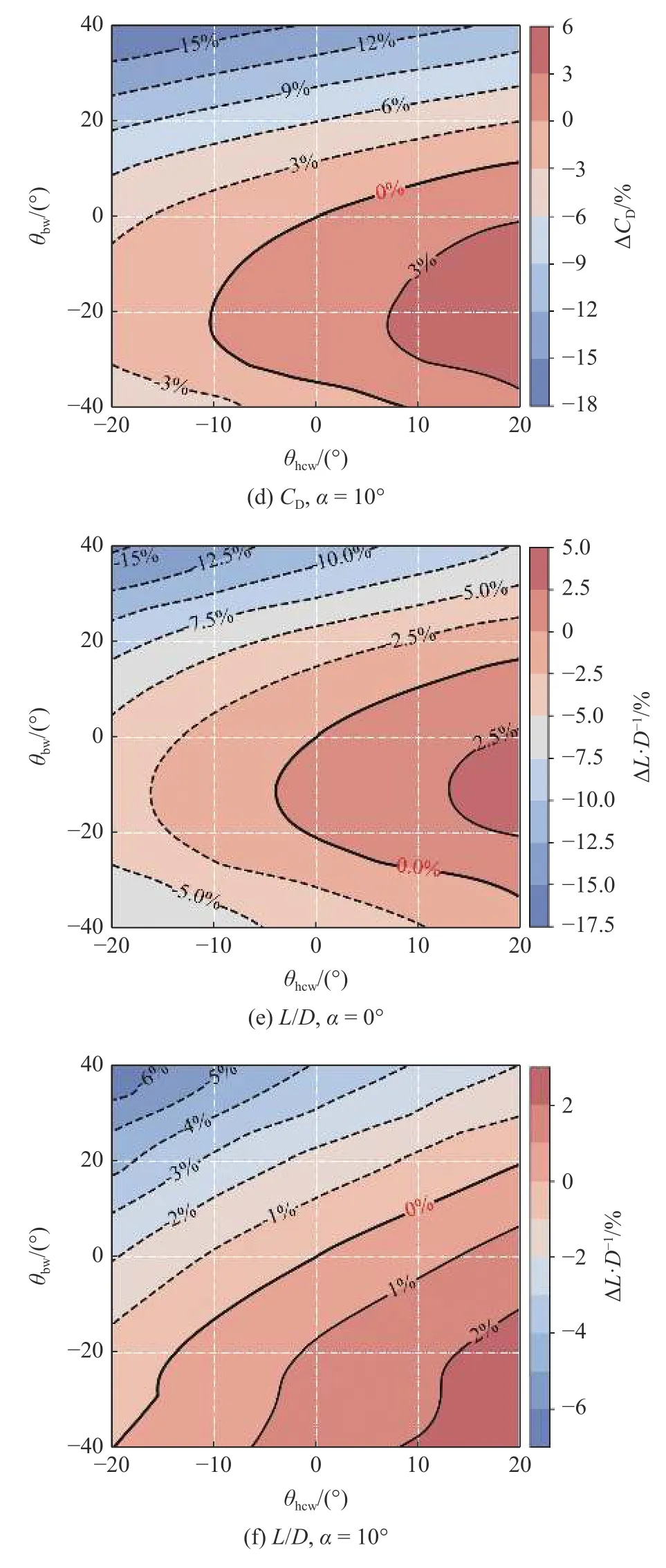
图9 设计空间内升、阻力系数及升阻比分布Fig.9 Lift coefficient,drag coefficient,and lift-drag ratio distribution in design space
从升力系数的分布来看,当 α=0°时,如图9(a)所示,一方面,升力系数随捕获翼下反角的增大而单调减小,随上反角的增大而单调增大;另一方面,升力系数随三角翼上反角的增大会单调减小,但随三角翼下反角的增大却呈现出“先增后减”的趋势,即三角翼存在临界下反角,三角翼略微下反有利于提高升力,但超过后升力将不增反降.就该构型而言,升力系数在设计空间内增量最大对应的翼反角约为 θhcw=20°,θbw=-5°,增幅约为4%,而三角翼上反且捕获翼下反将显著降低升力系数,最大降低约16%.当攻角增大到 α=10°时,如图9(b)所示,升力系数的变化趋势与 α=0°类似,但变化幅度会略微提高,且三角翼临界下反角会显著提高,此时不同捕获翼反角对应的均在 -25°左右.
对于阻力系数,从图9(c)可以看出,当 α=0°时,阻力系数主要对三角翼反角更敏感,捕获翼反角变化几乎不影响阻力;在整个设计空间内阻力系数最大仅变化了约5%,即此时翼反角对阻力系数的影响较小.然而,当攻角增大到 α=10°时,如图9(d)所示,翼反角对阻力系数的影响程度提高,此时阻力系数的变化趋势与升力系数类似,同样存在一个较为固定的三角翼临界下反角=-25°.
根据升力系数和阻力系数,可以得到升阻比分布,如图9(e)和图9(f)所示.当 α=0°时,升阻比随捕获翼下反角的增大而单调减小,随捕获翼上反角的增大而单调增大;三角翼存在临界下反角,当三角翼上反或下反角较大时,升阻比均会降低;在整个设计空间,仅当捕获翼上反且三角翼下反角在附近时,升阻比会增大,但最大增量仅在3%左右.整体来看,α=0°时升阻比的变化规律与升力系数一致,反映了小攻角时翼反角变化主要是通过影响升力系数进而改变升阻比的.与升力系数和阻力系数不同,随着攻角增大,翼反角对升阻比的影响反而会减弱,升阻比最大变化率从 α=0°时的15%降低到α=10°时的7%左右.当 α=10°时,在设计空间内尚不存在明显的三角翼临界下反角,当捕获翼上反或三角翼下反时,升阻比会略微增大.
4.2 纵向静稳定性分析
为研究翼反角对HCW 构型纵向静稳定性的影响,选用焦点位置Xac这一参数来度量纵向静稳定性的大小,当焦点后移时,即Xac值增大,说明纵向静稳定性增强;反之则说明纵向静稳定性减弱.
图10(a)和图10(b)分别给出了攻角 α=0°和5°时设计空间内焦点位置Xac分布,可以看出,当α=0°时,焦点位置受三角翼反角的影响比捕获翼反角更加显著,但总体影响有限;当捕获翼上反时,焦点后移,即纵向稳定性增强,反之则纵向稳定性减弱;当三角翼上反时,焦点前移,即纵向稳定性减弱;当三角翼下反时,焦点后移,但变化量很小,最大仅在1% 左右,即纵向稳定性受三角翼下反角的影响较小.当攻角增大到 5°时,焦点位置受捕获翼反角的影响有所增强,但整体规律不变.
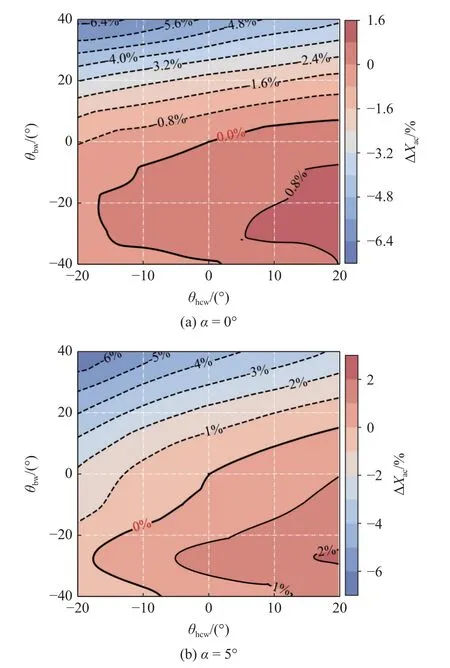
图10 设计空间内焦点位置分布Fig.10 Aerodynamic center position distribution in design space
4.3 横航向静稳定性分析
飞行器横航向稳定性通常由Clβ,Cnβ,CnβDYN和LCDP这4 个参数进行评估[34],其中Clβ和Cnβ分别表示横向和航向的单通道静稳定性导数;CnβDYN为偏航动态失稳参数,表征飞行器无控状态下横航向开环稳定特性,其在Cnβ的基础上,考虑了横向稳定性对飞行器航向稳定性的耦合增益,且该增益随飞行器转动惯量之比Iz/Ix及飞行攻角的增加而增大;LCDP为滚转操纵偏航失稳参数,表征滚转操纵时横航向闭环稳定特性,该判据与控制策略密切相关[35].考虑到CnβDYN计算时与质量特性密切相关,且该参数实质上仍然是静态稳定参数;而LCDP 求解过程涉及许多操纵稳定性导数,计算较为复杂,因此通过Clβ和Cnβ两参数评估翼反角对HCW 构型亚声速条件下横航向静稳定性的影响.
值得说明的是,在图2 所示的机体坐标系下,Clβ<0 表示横向静稳定,Clβ> 0 表示横向静不稳定,Clβ值越小表示横向静稳定性越强;Cnβ> 0 表示航向静稳定,Cnβ< 0 表示航向静不稳定,Cnβ值越大表示航向静稳定性越强.
图11(a)和图11(b)分别给出了攻角 α=0°,10°时Clβ分布,为了方便比较,图中红色数值表示基准构型的计算结果.可以看出,当 α=0°时,Clβ随捕获翼或三角翼下反角的增大而增大;另一方面,Clβ对捕获翼上/下反角的敏感度基本相同,而对三角翼的下反角相比其上反角更加敏感.对于大攻角 α=10°,捕获翼反角对Clβ的影响较小,此时Clβ对三角翼下反角更加敏感;随着三角翼上反角增大,Clβ开始会逐渐减小,但当 θbw>30°,Clβ基本保持不变.
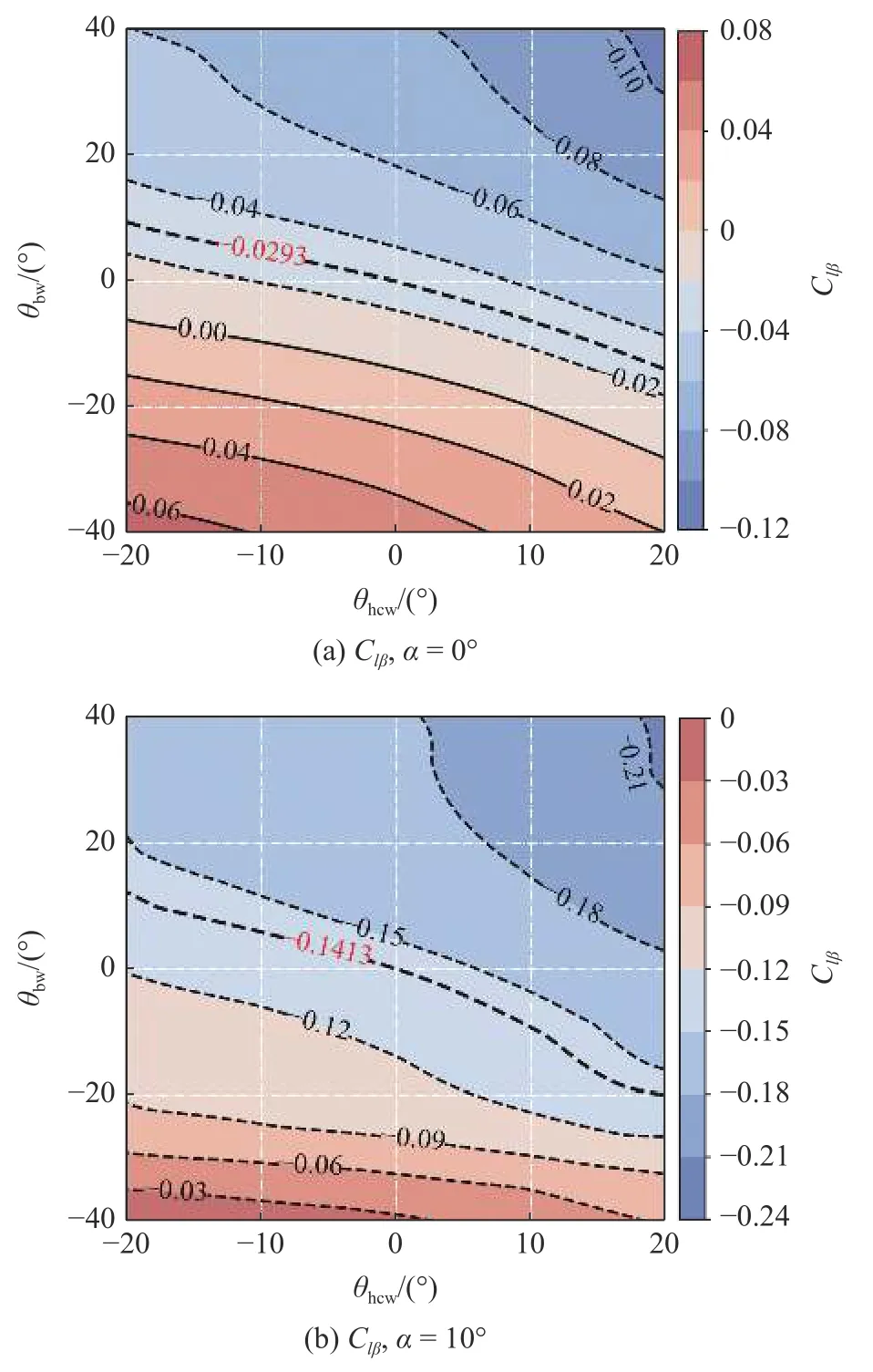
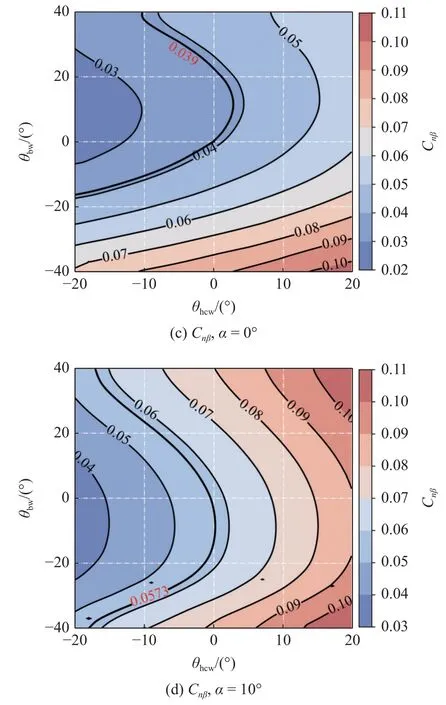
图11 设计空间内Clβ和Cnβ分布Fig.11 Clβ,Cnβdistribution in design space
整体来看,横向静稳定性受三角翼反角的影响比捕获翼更大;无论捕获翼还是三角翼,下反均会使飞行器横向静稳定性减弱,上反则使横向静稳定性增强;在大攻角状态时,当三角翼上反角增大到一定程度,横向静稳定性基本不再提升.
对于航向静稳定性,从图11(c)可以看出,在小攻角 α=0°时,捕获翼下反则Cnβ单调减小,上反则Cnβ单调增加;三角翼下反时,Cnβ单调增加,而上反则Cnβ呈现出先减后增的趋势;在整个设计空间中,Cnβ最小值对应于捕获翼下反 20°且三角翼上反10°左右;整体来看,三角翼反角对Cnβ的影响比捕获翼更大.进一步,从图11(d)可以看出,在大攻角α=10°下,Cnβ随捕获翼上/下反的变化趋势和小攻角状态一致,但Cnβ对捕获翼反角相比三角翼更加敏感;三角翼上反时,Cnβ单调增加,而下反则Cnβ呈现出先略微减小后迅速增大的趋势,即与小攻角下的变化规律发生了明显变化.
由此可见,在亚声速飞行时,捕获翼下反会减弱航向静稳定性,而上反则会增强,且捕获翼反角对航向静稳定性的这种影响规律在一定攻角范围内是一致.而对于三角翼,航向静稳定性随其反角的变化规律对攻角相对更加敏感,小攻角时,三角翼上反角增大,航向静稳定性将先减弱后增强,而下反则会明显提高航向静稳定性;攻角较大时,三角翼上反却更容易提高航向静稳定性,而随着下反角增大,航向静稳定性则呈现出先略微减弱后迅速增强的趋势.
从翼反角对横航向稳定性的影响程度上看,在小攻角 α=0°状态时,捕获翼上/下反对横向稳定性的影响比航向略大,而在大攻角 α=10°状态时,捕获翼上/下反对航向稳定性的影响更大;对于三角翼,在两个攻角状态下,其上/下反对横向稳定性的影响都更强.
4.4 流场分析
为了进一步探寻翼反角对HCW 构型亚声速气动特性的影响机理,本节结合不同构型典型工况下的流场结果,对前述相关现象进行说明.为了包含捕获翼和三角翼上/下反两种情况,鉴于篇幅有限,本节的流场分析主要针对无反的基准(basic)构型、上反(dihedral)构型和下反(anhedral)构型展开,其中上反构型两翼面均上反,对应翼反角 θhcw=11°,θbw=24°;下反构型两翼面均下反,对应翼反角θhcw=-11°,θbw=-24°.
图12 给出了在α=0°,β=0°时不同构型机体上、下表面的压强分布,可以看出,机体上表面的高压区主要集中在机身前体以及尾部,低压区主要分布在机身中部以及三角翼偏折段;机体下表面压强从前缘到尾缘逐渐减小,但整体较高.不同构型间机体上表面压强分布近似,下表面压强分布差异较大,且主要体现在翼面偏折段的前缘附近,三角翼上反使得下表面高压区范围减小;反之,下反使得高压区范围增大.图13 给出了捕获翼上、下表面的压强分布,可以看到捕获翼上表面整体压强更高,下表面压强呈现中心底边缘高的分布.不同构型间捕获翼下表面压强分布近似,上表面压强分布差异主要集中在尾缘,且捕获翼上反使得上表面高压区范围减小;反之,下反使得高压区范围增大.
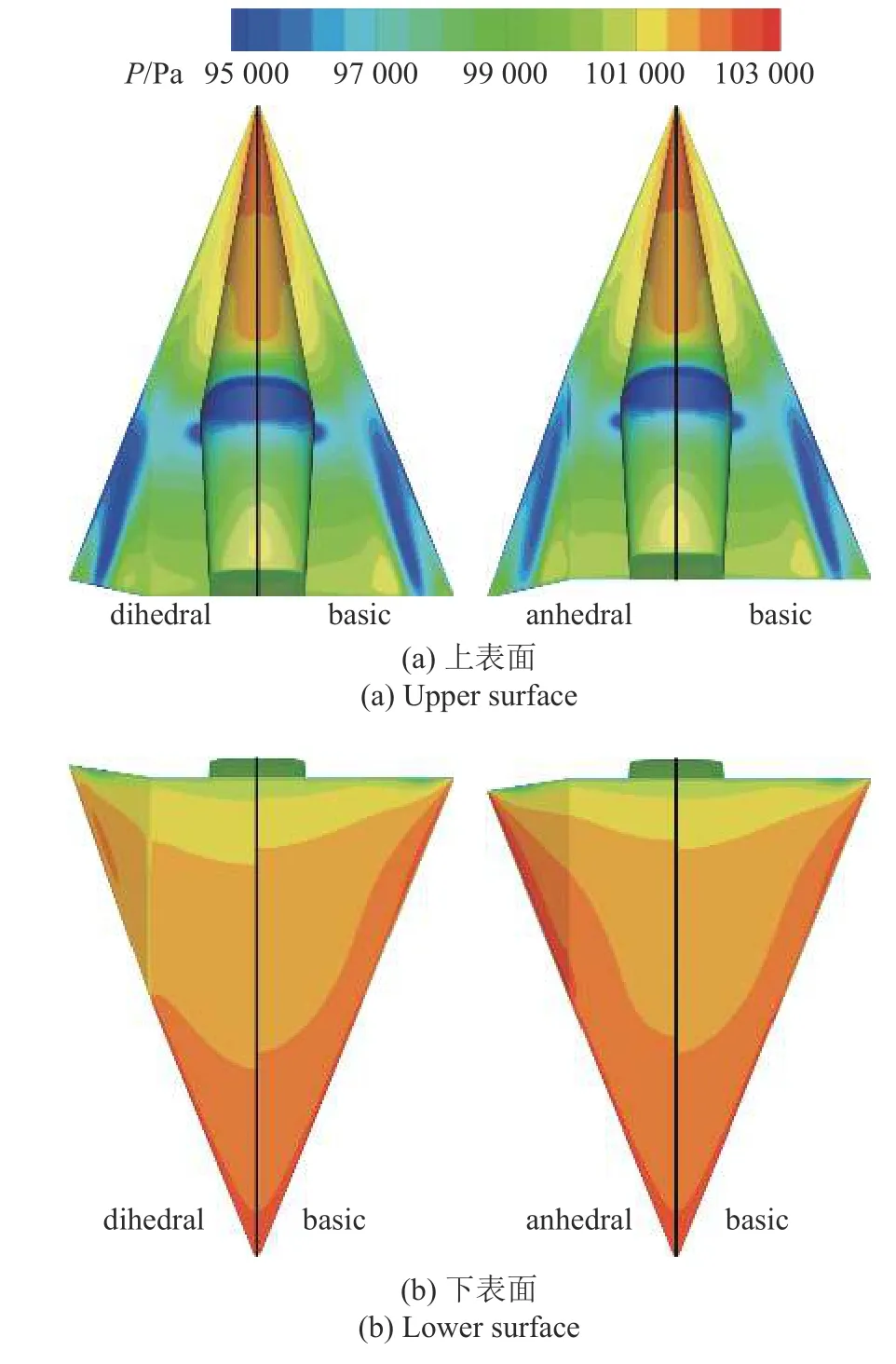
图12 机体上、下表面压强分布 (α=0°,β=0°)Fig.12 Pressure distributions on the upper and lower surface of bodies(α=0°,β=0°)

图13 捕获翼上、下表面压强分布 (α=0°,β=0°)Fig.13 Pressure distributions on the upper and lower surface of HCWs(α=0°,β=0°)
考虑到升、阻力是由物面压强差和投影面积两因素综合决定的,当三角翼下反时,两因素对升、阻力的影响是相反的.具体来说,当三角翼下反角小幅增加时,此时投影面积的改变很小,上、下表面压强差对升、阻力起主导作用,升、阻力均会增加;而当三角翼下反角超过某一临界值时,此时投影面积将对升、阻特性起主导作用,如法向投影面积减小会导致升力降低,轴向投影面积减小会导致阻力降低.当三角翼上反时,物面压强差和投影面积的变化均会导致升、阻力减小,因此升、阻力将在两者共同作用下单调变化.另一方面,捕获翼上/下反时投影面积的变化较小,因此其提供的升、阻力主要受压强变化主导.综合以上分析,翼反角对升阻特性的影响规律如4.1 节所述.
在亚声速大攻角飞行时,该构型背风面旋涡会对气动性能产生影响.图14 给出了在 α=10°,β=0°时不同构型机体上表面的压强分布及不同切面的流场涡量 ‖ω‖,可以看出,捕获翼上表面的旋涡尚未完全发展起来,呈现出不规则的形状;而不同构型机体背风面均具有明显的涡结构,旋涡沿三角翼前缘从机体头部一直延伸到尾部,造成三角翼两侧出现大范围的低压区.当三角翼上反时,旋涡强度下降,导致三角翼上表面低压区的范围减小;反之,三角翼下反时,旋涡强度增加,甚至出现了较强的二次涡和翼尖涡结构,导致低压区范围明显增大.
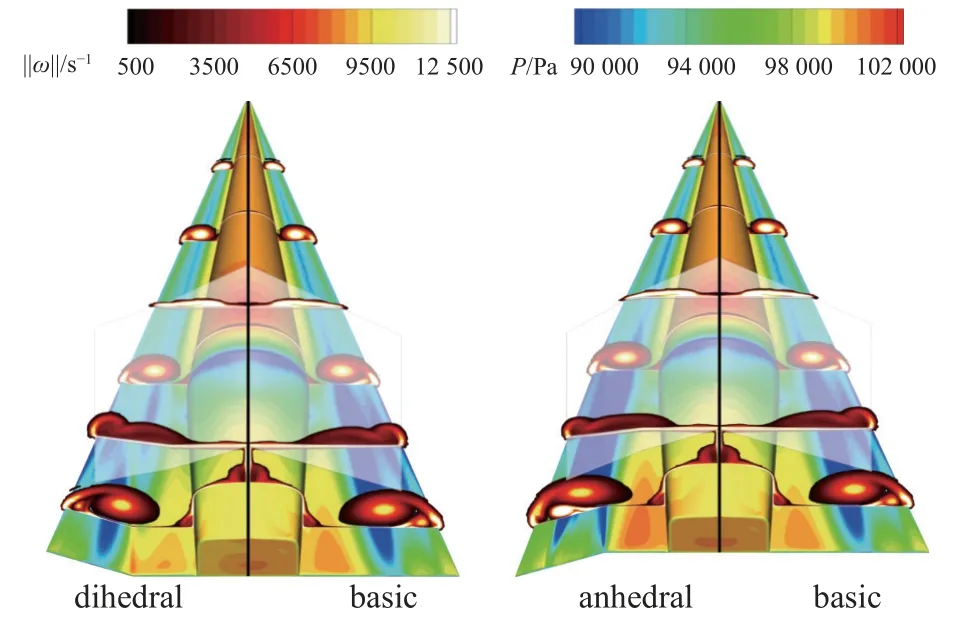
图14 机体上表面压强分布及涡结构 (α=10°,β=0°)Fig.14 Pressure distributions on the upper surface of bodies and vortexstructures (α=10°,β=0°)
进一步,考虑侧滑角对流场的影响,图15 给出了在 α=10°,β=5°时3 种构型机体上、下表面的压强分布及不同切面的流场涡量 ‖ω‖ .可以看出,对于上表面,不同构型间三角翼两侧涡结构一致,均由头部沿三角翼前缘向尾部延伸,且旋涡强度的差异决定了两侧低压区的形态.不同构型间上表面压强分布差异主要体现在三角翼偏折段的低压区及尾部翼根处的高压区.相对于基准构型,三角翼上反使得上表面偏折段低压区明显减弱,尾部翼根高压区范围减小,两侧压强差异减小,综合导致滚转恢复力矩增大,横向稳定性提高;三角翼下反使得上表面偏折段低压区明显增强,尾部翼根高压区范围增大,两侧压强差异增大,综合导致横向稳定性降低.从图15 下表面压强分布也可以看出,不同构型间下表面左侧高压区分布较为一致,差异主要体现在右侧翼面偏折处附近,三角翼上反使得右侧偏折处压强明显降低,恢复滚转力矩增大,横向稳定性提高.

图15 机体上、下表面压强分布及涡结构 (α=10°,β=5°)Fig.15 Pressure distributions on the upper and lower surface of bodies and vortex structure (α=10°,β=5°)
下面考察侧滑角对捕获翼表面压强的影响,图16给出了在 α=10°,β=5°时3 种构型捕获翼上、下表面的压强分布.可以看出,不同构型间上表面右侧压强分布变化较小,差异主要体现在左侧翼面尾缘附近的高压区;对于不同构型间下表面压强分布的差异,一方面体现在左侧翼面尾缘附近高压区,另一方面体现在右侧翼尖附近的高压区.相对基准构型,捕获翼上反导致上表面左侧压强降低,下表面左侧压强降低且右侧压强升高,虽然上、下表面贡献的滚转力矩是相反的,但由于上表面压强变化更显著一点,因此综合导致恢复滚转力矩小幅增加,即横向稳定性稍微提高.此外,由于捕获翼左侧偏折段上、下表面的压差比右侧大,因此偏航力矩主要受左侧影响,当捕获翼上反时,综合导致左侧贡献的恢复偏航力矩增加,航向稳定性提高.同理,捕获翼下反时将导致横向、航向稳定性都降低,此处不再赘述.

图16 捕获翼上、下表面压强分布 (α=10°,β=5°)Fig.16 Pressure distributions on the upper and lower surface of HCWs(α=10°,β=5°)
5 结论
本文基于高压捕获翼新型气动布局的基本原理,设计了一种机身-三角翼组合、单立板支撑布局的高压捕获翼概念构型.以捕获翼和三角翼的上/下反角为设计变量并构建参数化几何模型,结合均匀试验设计方法、CFD 数值模拟方法和Kriging 代理模型方法,研究了0°~ 10°攻角状态下翼反角对高压捕获翼构型亚声速气动特性的影响,主要结论如下.
(1) 升阻特性方面,小攻角状态下翼反角对升阻比的影响比大攻角更加显著;捕获翼上反时,升阻比略微增加,下反升阻比则减小;三角翼上反时,升阻比减小,下反时升阻比先略微增大,直到超过某临界下反角后,将不增反降;整体来看,升阻比的改变主要受升力主导.
(2) 三角翼上反对该构型静稳定性的综合增益相比下反更显著.一方面,三角翼上反时,纵向稳定性略微减弱,但横向和航向稳定性均会增强,但在较大攻角时,上反角过大可能对横向稳定性的提升有限;另一方面,三角翼下反时,纵向稳定性基本不变,航向稳定性会增强(尤其在小攻角状态下效果更强),但横向稳定性会明显减弱.
(3) 捕获翼上反对增强该构型静稳定性的综合效果相比下反更好.从变化规律上看,捕获翼上反时,纵向、横向和航向稳定性均会有所增强,下反则纵向、横向和航向稳定性均减弱.
(4) 从提高该构型亚声速状态下三通道稳定性的角度来看,捕获翼和三角翼同时上反这种组合相对较优,当然,上反角度还需要根据具体的外形进行详细设计.

