基于卷积降噪自编码器的雷达信号智能分选

洪淑婕，孙闽红，王之腾，仇兆炀

(1. 杭州电子科技大学通信工程学院，浙江 杭州 310018； 2. 陆军工程大学通信工程学院，江苏 南京 210001)

0 引言

现代电子战中雷达侦察所面临的电磁环境日趋复杂，给雷达信号分选带来了严峻挑战。现有的雷达信号分选方法，大多是基于雷达脉冲描述字，采用改进的序列差值直方图算法(sequential difference histogram, SDIF)算法[1]、累积差值直方图算法(cumulative difference histogram, CDIF)[2]、PRI变换法[3-5]和扩展关联分选方法[6]等实现。然而，以上方法存在应用范围局限性较大，对复杂电磁环境鲁棒性差的问题。

近年来，基于深度学习的智能信号分选得到了广泛关注。文献[7]提出了一种基于轨迹特征和长短时记忆网络的分选方法；文献[8]提出了一种将预处理的时频图像结合迁移学习模型的信号分选方法；文献[9]提出了一种改进的DNN分选算法；文献[10]提出了一种基于集成深度学习的分选算法。然而，这些方法存在低信噪比条件下分选性能下降，不适用于复杂电磁环境等问题。

针对上述不足，本文提出一种基于卷积降噪自编码器的雷达信号智能分选算法。卷积降噪自编码器因其降噪处理能力而受到关注。文献[11]利用卷积降噪自编码器高效降低红外图像常见混合噪声；文献[12—13]利用卷积降噪自编码器实现地震数据的同步重建和去噪。卷积降噪自编码器不但能在全局上把握整体的变化特征，还可以提取局部特征，使提取到的特征更具鲁棒性。本文算法仅利用TOA一个参数，将雷达脉冲分为目标脉冲和其他脉冲，其他脉冲相对于目标脉冲则视为噪声，将脉冲进行编码并转化为二维图像，使用卷积降噪自编码器学习目标脉冲序列的内部时间模式以完成脉冲分选。

1 基础知识

1.1 降噪自编码器

与自编码器不同的是，降噪自编码器通过克服噪声的干扰重构出被噪声污染前的原始数据，这样有效改善了自编码器的过耦合问题，增强了泛化能力。典型的降噪自编码器结构如图 1所示。

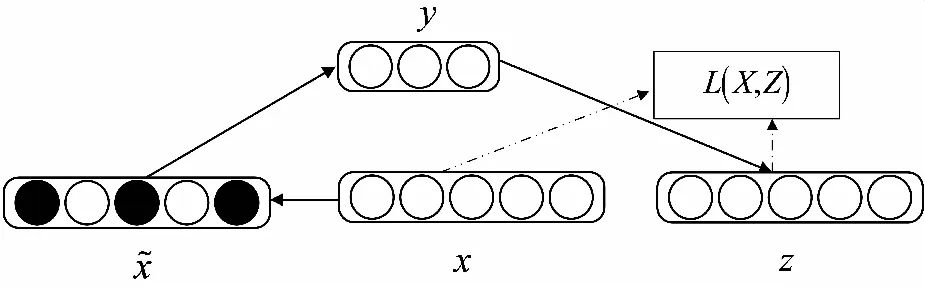
图1 降噪自编码器模型Fig.1 The denoising autoencoder framework

降噪自编码器由编码层和输出层组成，编码器用于将输入映射到低维特征空间，而解码器将低维特征空间中数据映射回原始输入。降噪自编码器的工作原理定义为

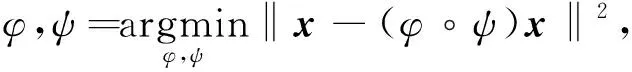
(1)

式(1)中，I和F分别表示输入空间和特征空间，φ为编码器，ψ为解码器，(φ·ψ)x为自编码器的输出，‖·‖为Frobenius范数。假设输入为x∈I，将其映射到y∈F。它的编码过程和解码过程分别为

(2)

z=σ′(W2y+b2)，

(3)

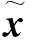
降噪自编码器的目标是寻找使得输入与输出的残差最小的过程，其目标函数为

(4)

式(4)中，m为网络中样本数量。

1.2 卷积降噪自编码器

卷积形式的降噪自编码器和全连接形式的降噪自编码器的差别在于网络相邻两层的连接方式。卷积降噪自编码器用卷积层和池化层替代了传统降噪自编码器中的全连接层。卷积降噪自编码器结构如图2所示，该结构中的编码器部分由两个卷积层和两个池化层组成，解码器部分由两个反卷积层和两个上采样层组成。

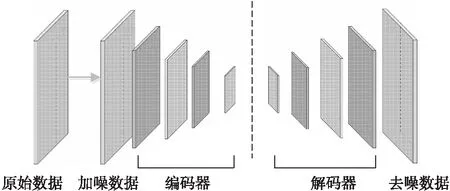
图2 卷积降噪自编码器模型Fig.2 The convolutional denoising autoencoder framework

卷积降噪自编码器在空间复杂度上大大优于降噪自编码器。卷积神经网络的空间复杂度即总参数量和各层输出特征图尺寸。参数量为模型所有带参数的层的权重参数总量[14]，空间复杂度为

(5)

式(5)中，总参数量只与卷积核的尺寸K、通道数C、卷积层数D相关，l为网络中的卷积层序号，Cl为第l个卷积层的卷积核个数，M是每个卷积核输入特征图的边长。

输出特征图尺寸由输入矩阵尺寸X、卷积核尺寸K、填充P(Padding)和步长S(Stride)四个参数决定，具体如下所示：

M=(X-K+2P)/S+1。

(6)

全连接层的空间复杂度与输入数据的尺寸密切相关，因此如果输入图像尺寸越大，模型的体积就越大，如下式所示[15]：

Space～O(X2·Cin·Cout)。

(7)

本文采用的降噪自编码器和卷积降噪自编码器的各层参数如表1和表2所示，输入均为28×28×1的图像。

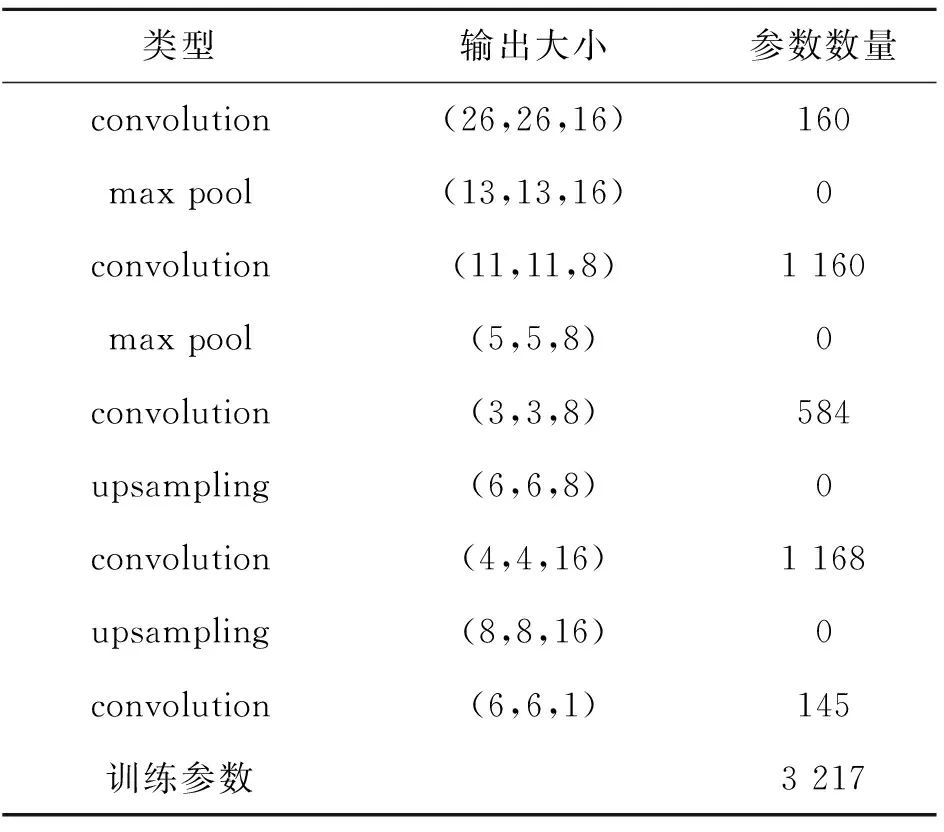
表1 卷积降噪自编码器各层参数Tab.1 The parameters of convolutional denoising autoencoder framework

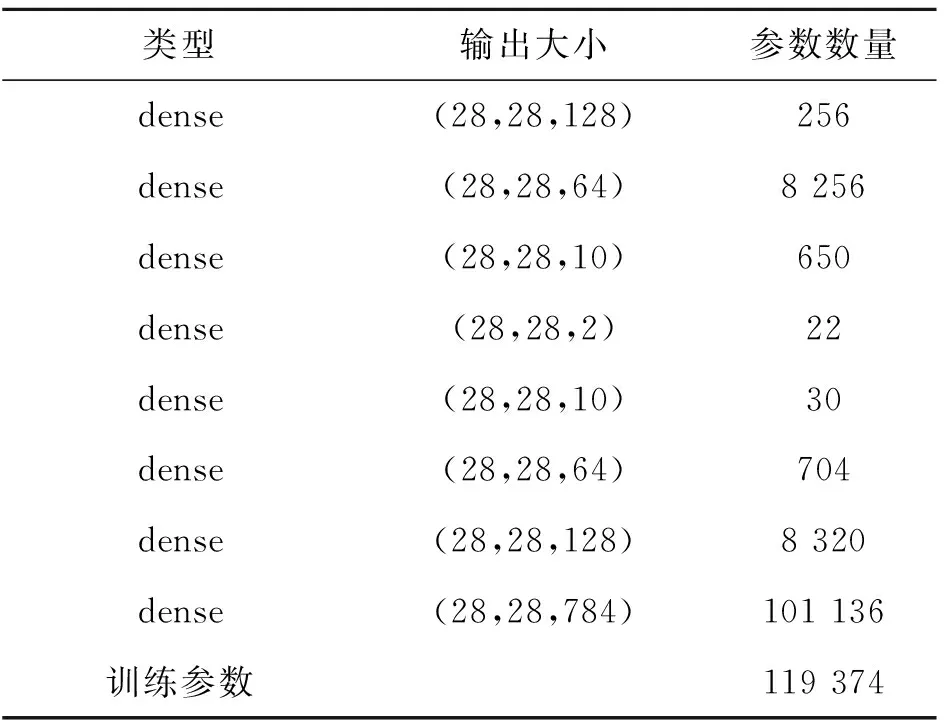
表2 降噪自编码器各层参数Tab.2 The parameters of denoising autoencoder framework

由表1和表2可知，降噪自编码器和卷积降噪自编码器训练参数数量分别为119 374和3 217，卷积降噪自编码器训练参数数量仅为降噪自编码器训练参数数量的3%，大幅减少了训练参数的数量，有效地防止训练的过拟合。

同时，由于雷达信号分选过程中不仅要学习脉冲序列的PRI模式，还会遇到漏脉冲、参差脉冲等复杂情况，需要关注局部特征，卷积降噪自编码器能更好地捕捉像素和其周围像素的联系，提取更具鲁棒性的特征，所以本文选择卷积降噪自编码器作为训练网络。

2 基于卷积降噪自编码器的雷达信号智能分选

2.1 算法步骤

本文所提出的基于卷积降噪自编码器的雷达信号智能分选方法将每部雷达的脉冲流看作受噪声污染的子流，因此信号分选可视为去噪。该方法流程如图3所示。

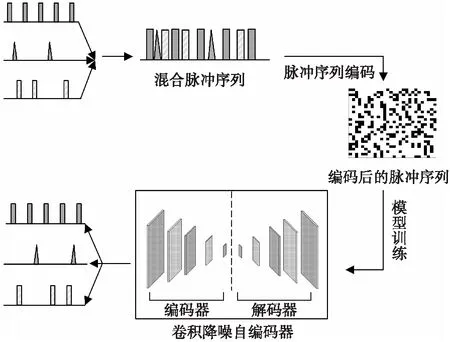
图3 基于卷积降噪自编码器的雷达信号分选流程图Fig.3 Radar signal sorting flow chart based on convolutional denoising autoencoder

具体实现步骤如下：

1)将各部雷达的脉冲TOA序列T={t1,t2,…,ti,…,tN}进行数字化转化为二进制编码向量x。其中ti表示该部雷达第i个脉冲到达的时间，N是截获脉冲的数量。

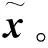
4)将复杂电磁环境下的混合脉冲TOA序列(即测试数据)输入训练好的卷积降噪自编码器模型进行脉冲分选得到目标雷达脉冲序列。

2.2 脉冲序列编码

最常用的雷达信号分选参数通常都是脉冲描述字，其一般构成是脉冲到达时间、脉冲方向角、脉冲频率、脉冲宽度和脉冲幅度[16]。脉冲序列的PRI模式是将不同雷达脉冲序列区分开来的最明显的特征[14]。由于不能由接收机直接获得PRI，因此TOA经常被用于测量PRI以获得脉冲序列的PRI模式。TOA序列经过编码后的图像可以很好地展示脉冲的相对位置，便于获取脉冲序列的时间序列模式，同时可及时发现漏脉冲和参差脉冲。因此本文采用TOA序列作为雷达信号分选的参数。

由于脉冲到达时间的不断增大，使得TOA序列最终增大到一个较大的值，为了让神经网络模型尽可能轻松地处理输入，本文将TOA序列转换为只有0和1的二进制编码，线性数字化后的TOA序列可接受一定的量化误差。本文采用了一种如式(8)所示二进制数字编码，给定一个单位tunit，脉冲序列T根据tunit进行线性数字化，使其在[0,M·tunit]范围内，M是脉冲序列的总单位数。

(8)

假设一部雷达的PRI调制模式为参差，PRI值为[100,150,50]，tunit设为50，则TOA序列表示为T=[100,250,300,400,550,600,…]，根据式(8)脉冲序列T被编码为[0,1,0,0,1,1,0,1,0,0,1,1,0,1,…]。将脉冲编码转化为28×28的图像如图 4所示，编码图像即为卷积降噪自编码器的输入。

图4 脉冲编码示例Fig.4 An example of pulse coding

3 实验与结果分析

为了验证存在丢失脉冲、参差脉冲、TOA估计误差以及不同信噪比的复杂电磁环境中本文方法的有效性，本文进行了一系列仿真实验。

3.1 实验环境及参数设置

神经网络训练参数如下:训练批次1 000，batch_size为128，使用交叉熵作为损失函数，优化器为Adam，同时为了避免实验的偶然性，设置蒙特卡洛仿真次数为100次。

实验数据均通过Matlab 2018b编程实现，4部雷达的具体参数设置如表3所示。为了更贴合实际电磁环境，设置一定脉冲丢失率、脉冲参差率和TOA估计误差。

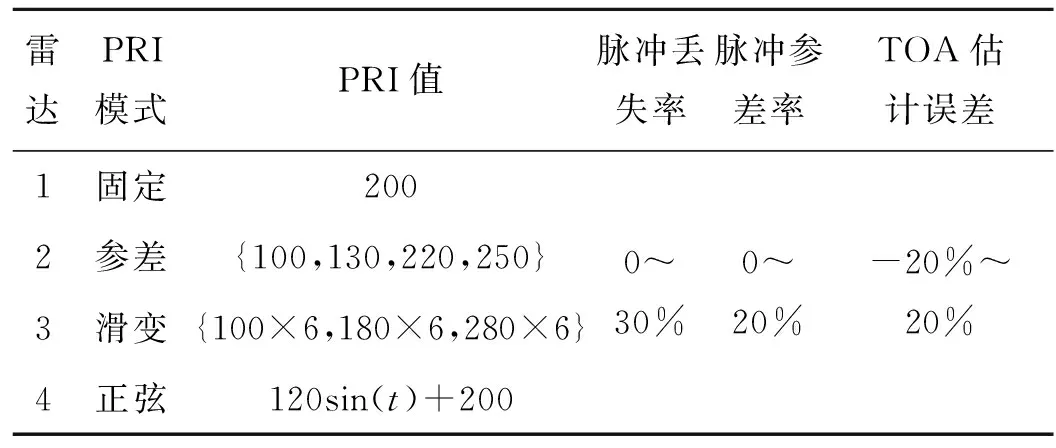
表3 雷达参数设置表Tab.3 Parameter table of radar

仿真生成4部雷达的脉冲序列，每部雷达生成10 000个脉冲序列，将4部雷达每个样本的脉冲根据其到达时间的先后进行排序构造混叠脉冲序列，然后将混叠脉冲序列根据式(8)进行数字化转化为二进制编码向量，该二进制编码向量即为样本集，训练集为随机抽取的7 000个样本，测试集为剩余样本。

同时，为验证本方法的先进性，与文献[1]中的SDIF方法和文献[2]中的PRI变换方法这2种有代表性的方法进行了性能比较。

3.2 仿真实验与分析

实验1 验证分选方法在不同信噪比下的分选性能

测试样本的信噪比变化范围为[-15 dB,15 dB]，得到三种分选方法的分选结果如图5所示。图6给出了信噪比为5 dB时雷达2的样本示例。

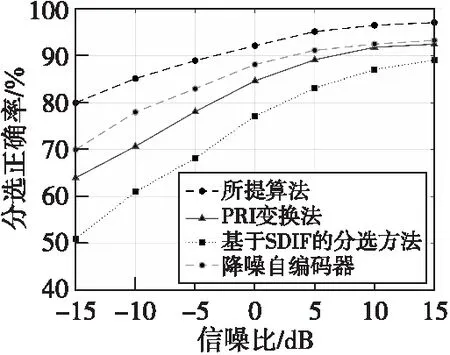
图5 不同信噪比下的分选性能对比Fig.5 Sorting performance comparison under different SNR conditions

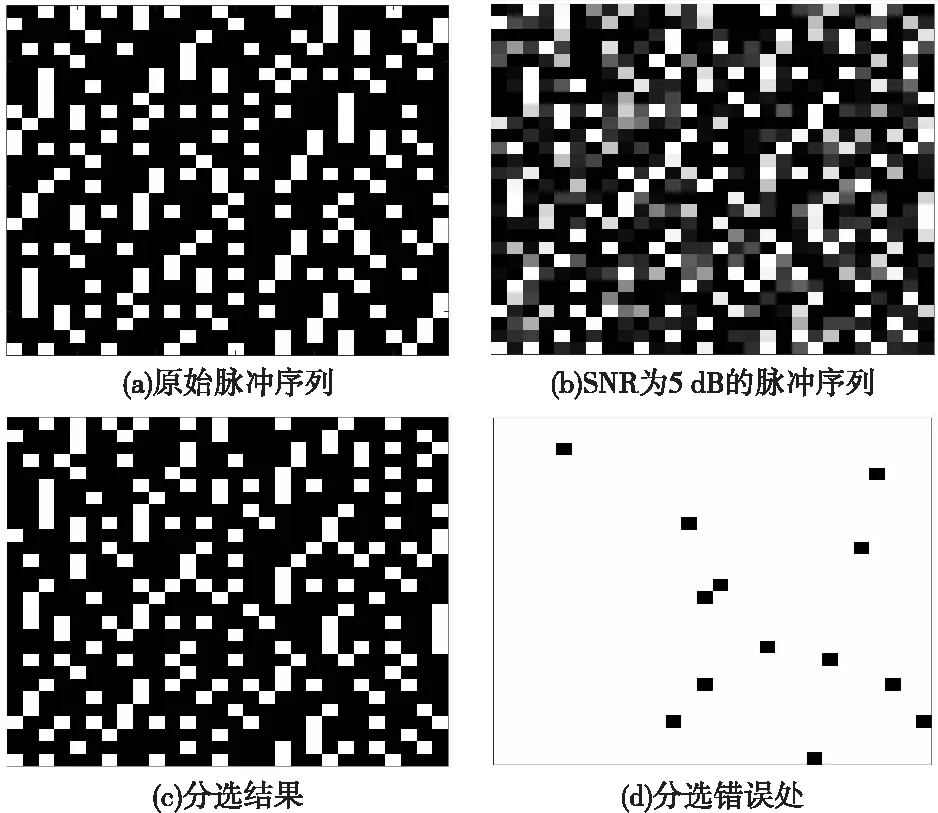
图6 信噪比为5 dB的样本示例Fig.6 Sample example under SNR is 5 dB

图5表明，本文方法的分选正确率和使用降噪自编码器相比平均提高了6.1%，在低信噪比时性能提高更明显，在信噪比为-15 dB时性能改善了10%，表明本文方法仅使用了降噪自编码器3%的训练参数获得了更高的分选正确率，体现了卷积降噪自编码器在性能方面的优越性。同时该方法与PRI变换法和基于SDIF的分选方法相比分别提高了10.2%和17%，能够有效地改善低信噪比环境下雷达信号分选性能。

实验2 验证在不同脉冲丢失率下不同分选方法的分选性能

测试样本的脉冲丢失率按照0～30%递增，得到三种分选方法的分选结果如图7所示。脉冲丢失率为5%的样本示例如图8所示。

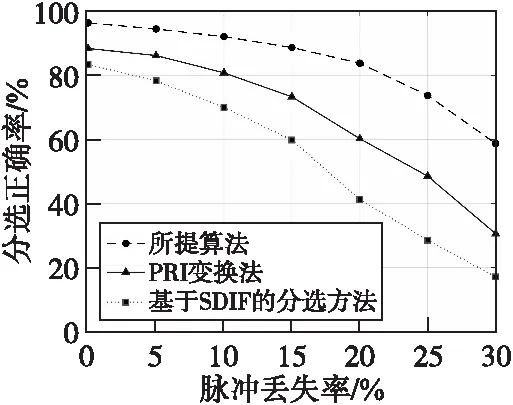
图7 不同脉冲丢失率下的分选性能对比Fig.7 Sorting performance comparison under different pulse lose rate conditions

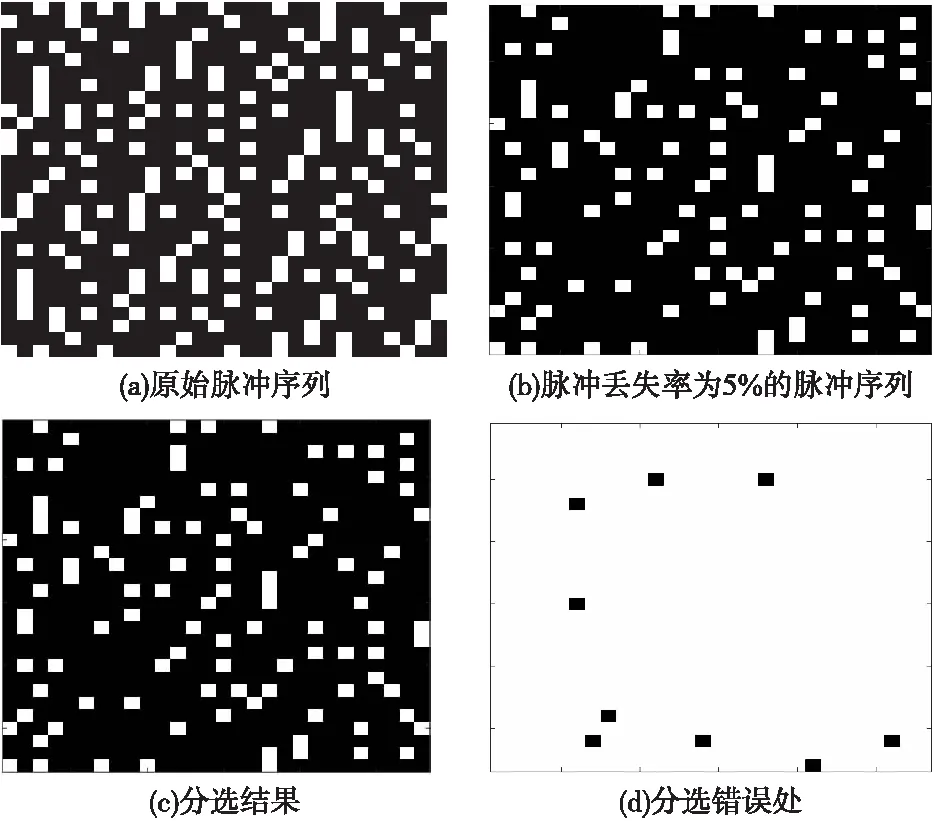
图8 脉冲丢失率5%的样本示例图Fig.8 An example of the samples when pulse lose rate is 5%

图7表明，随着脉冲丢失率的增大，三种分选方法的分选正确率呈下降趋势。与PRI变换法和基于SDIF的分选方法相比，本文方法的分选正确率分别提高了15.2%和24.6%，说明本文方法能够有效地改善脉冲丢失环境下的雷达信号分选性能。

实验3 验证在不同脉冲参差率下不同分选方法的分选性能

测试样本的脉冲参差率按照0～20%递增，得到三种分选方法的分选结果如图9所示。脉冲参差率为5%的雷达2的样本示例如图10所示。

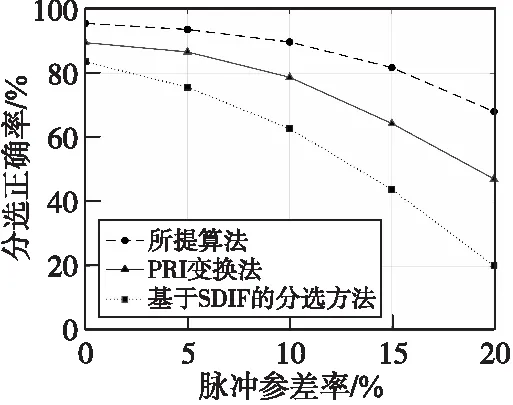
图9 不同脉冲参差率下的分选性能对比Fig.9 Sorting performance comparison under different pulse spurious rate conditions

图10 脉冲参差率5%的样本示例图Fig.10 An example of the samples when pulse spurious rate is 5%

图9表明，本文方法在脉冲参差率小于15%时分选正确率能达到90%以上。与PRI变换法和基于SDIF的分选方法相比，正确率分别提高了12.4%和21.8%，说明本文方法能够有效地改善脉冲参差环境下的雷达信号分选性能。

实验4 验证在不同TOA估计误差下不同分选方法的分选性能

测试样本的TOA估计误差按照0～20%递增，得到三种分选方法的分选结果如图11所示。TOA估计误差为20%的样本示例如图12所示。

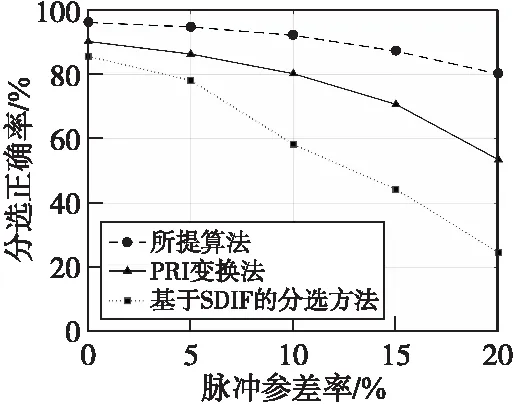
图11 不同TOA估计误差下的分选性能对比Fig.11 Performance comparison of different sorting methods

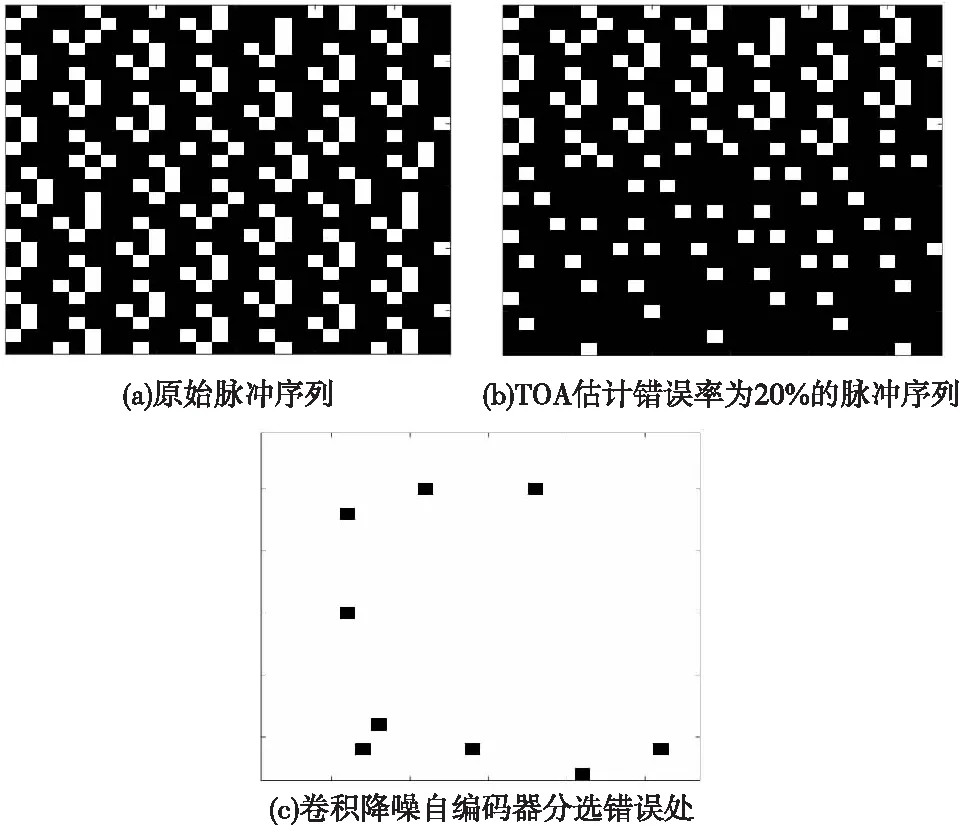
图12 TOA估计错误率20%的样本示例Fig.12 An example of the samples when TOA estimation error rate is 20%

图11表明，基于SDIF的分选方法和PRI变换法在低TOA估计错误率下可以达到较高的分选准确率，但TOA估计错误率的增大导致脉冲序列断裂，并没有很好地实现序列搜索和提取，因此并不具备良好的分选效果。而本文方法的分选正确率与PRI变换法和基于SDIF的分选方法相比分别提高了13.8%和25.7%，在估计错误率20%时仍可达到90%以上的分选正确率，表明了本文所提方法的优越性。

在具有多功能雷达信号的复杂电磁环境中，多功能雷达工作模式的转换会影响雷达的PRI参数。为了更贴近实际作战场景，4部雷达设置的具体参数如表4所示。假设雷达1是多功能雷达，雷达2、3、4为单功能雷达。雷达1的工作模式包括搜索和跟踪，工作模式切换时PRI参数也会随之切换，搜索模式下的PRI值为90，跟踪模式下的PRI值为170。同时设置一定脉冲丢失率、脉冲参差率和TOA估计误差，并与文献[1—2]中使用TOA参数的传统方法及文献[9—10]中使用脉内特征的深度学习方法进行了性能比较。

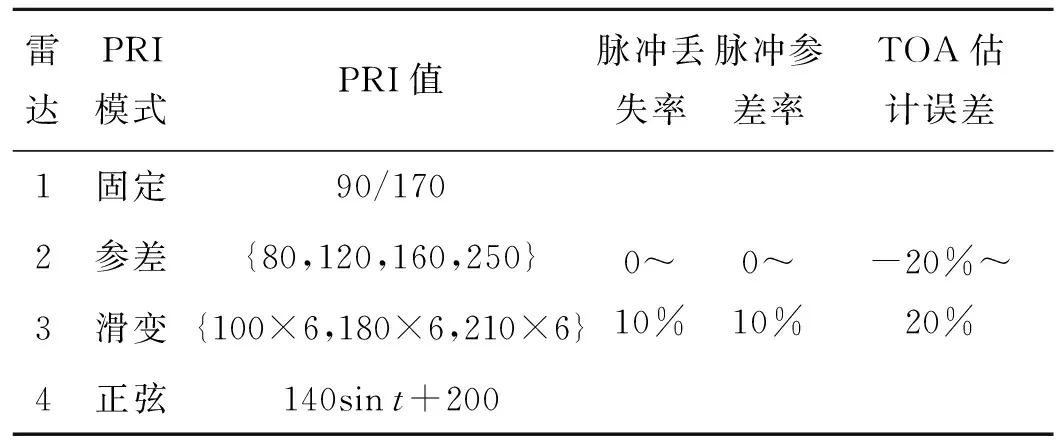
表4 雷达参数设置表Tab.4 Parameter table of radar

实验5 验证不同方法在多功能雷达条件下不同信噪比时的分选性能

测试样本的信噪比变化范围为[-15,15] dB，得到5种分选方法的分选结果如图13所示。

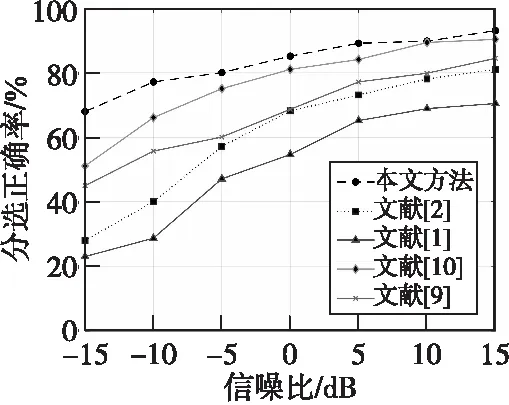
图13 不同信噪比下的分选性能对比Fig.13 Sorting performance comparison under different SNR conditions

图13表明，使用脉内特征的文献[9]和文献[10]在信噪比高时都可以达到较高的分选准确率，但由于脉内特征提取受到信噪比条件制约较大，导致脉内特征分析的能力缺失或变弱，因此在低信噪比条件下并不具备良好的分选效果。本文方法的分选正确率与文献[9]和文献[10]相比分别提高了16.4%和7.2%，与使用TOA参数的文献[1]和文献[2]相比，本文方法的分选正确率分别提高了22.8%和14.9%，说明本文方法在低信噪比条件下性能改善明显。

实验6 验证不同方法在多功能雷达条件下不同TOA估计误差时的分选性能

测试样本的TOA估计错误率按照0～20%递增，得到5种分选方法的分选结果如图14所示。

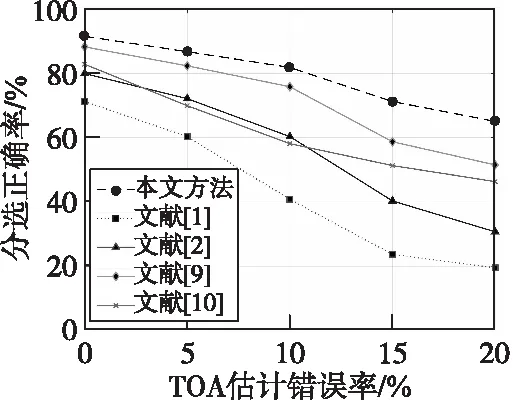
图14 不同TOA估计误差下的分选性能对比Fig.14 Performance comparison of different estimation error of parameters

图14表明，随着TOA估计误差的增大，五种分选方法的分选正确率呈下降趋势。与使用TOA参数的文献[1]和文献[2]相比，本文方法的分选正确率分别平均提高25.7%和16.7%，与使用脉内特征的文献[9]和文献[10]相比，本文方法的分选正确率分别平均提高了8.1%和18.2%。

4 结论

本文提出一种基于卷积降噪自编码器的雷达信号智能分选方法，该方法将其他脉冲序列视为噪声，目标脉冲序列视为待提取的数据。首先将脉冲序列到达时间进行编码，并将其转化为二进制编码向量，将编码向量输入卷积降噪自编码器学习目标脉冲序列的内部时间模式，再用训练后的网络对混合脉冲序列进行分选，提取出目标脉冲序列。通过仿真分析所提方法在复杂电磁环境下的分选性能，并与使用TOA参数的传统方法和使用脉内特征的深度学习方法进行对比。仿真结果表明，本文方法在考虑漏脉冲率、参差脉冲、TOA估计误差、信噪比等参数变化及存在多功能雷达信号的复杂电磁环境下的分选性能有了较大提升，证明了所提方法的优越性和有效性。