基于弹载磁传感器的地磁场畸变方向测量方法

张舒然，丁立波，肖 力，陈荷娟

(1.南京理工大学机械工程学院，江苏 南京 210094；2.驻重庆地区第二军事代表室，重庆 400000)

0 引言

铁磁性金属材料具有很高的磁导率，会引起局部地磁场的偏转，使其附近的地磁场强度和方向发生畸变。地磁场的畸变形式和畸变程度与目标结构、装甲材料厚度、目标与地磁矢量的相对位置关系有关。磁探测技术即基于噪声特性的磁异信号检测技术，主要是根据铁磁性金属的存在引起磁场的局部变化现象，利用磁传感器采集处理变化的磁异信号实现对铁磁性目标的检测、识别、跟踪与定位等[1]。

在磁场方向测量及磁探测技术应用方面，国外的技术研究开展较早，目前比较成熟的MAD磁异常探测装置主要装备在反潜飞机及反潜直升机上，用于探测舰艇及潜艇，如俄罗斯的K-27PL反潜直升机、英国的nimrod NR2反潜巡逻机、法国的Atl-2反潜直升机，美国P-3C飞机等，探测距离可达400～500 m[2]。国内对弱磁目标物体探测的研究起步相对比较晚，虽然也有机载MAD的应用，但探测精度不高。文献[3]根据磁偶极子梯度张量定位模型，利用一个测量点的测量值实现目标实时定位。文献[4]由磁偶极子梯度张量中间特征值和测量点与偶极子之间矢径的正交特性提出了定位方程，设计了磁梯度张量系统，用有限差分法近似磁场分量的一阶和二阶空间梯度，实现了对偶极子的定位。文献[5]研究了梯度张量单点定位算法，通过计算磁异常信号的特征值及其频率域垂直导数，对磁性目标体进行水平定位和边界识别。文献[6]提出了基于地磁总场阵列的目标定位方法，以光泵磁力仪构成定位阵列，通过测得运动目标产生的磁异常实现对运动磁目标的连续定位。文献[7]建立了单个磁梯度计旋转探测模型，基于此模型实现了对磁偶极子源的精确定位。

目前利用地磁场信息进行目标的探测及定位多用于对水下大型目标，且在理论研究方面大多还是基于磁场信息标量探测对目标进行定位。为探究在弹丸运动中仅利用地磁信息对空中目标进行定位的可行性，本文采用Ansys Maxwell软件，作静态磁场仿真，对路径上磁场方向的变化进行解算与研究，从而为进一步判断目标方位提供信息依据。

1 坐标系定义及变换

在磁场方向的测量计算过程中，涉及到地磁场矢量在多个坐标系之间的变换，根据地磁学和外弹道学的相关知识，对坐标系进行定义，确定其相互之间的变换关系，并推导磁场方向解算模型。

如图1所示，OXmYmZm为地磁坐标系，原点O为炮口中心，OXm轴沿水平线指向地理北，OYm轴沿水平线指向地理东，OZm轴垂直向下。假设地磁场矢量为H，其强度为H，磁偏角ζ为OXm与地磁场矢量在OXmYm面内的投影的夹角(以正北方向为零度基准，北偏东为正)，磁倾角ε为地磁场矢量与其在OXmYm面内的投影的夹角(以水平为零度基准，低头为正)。

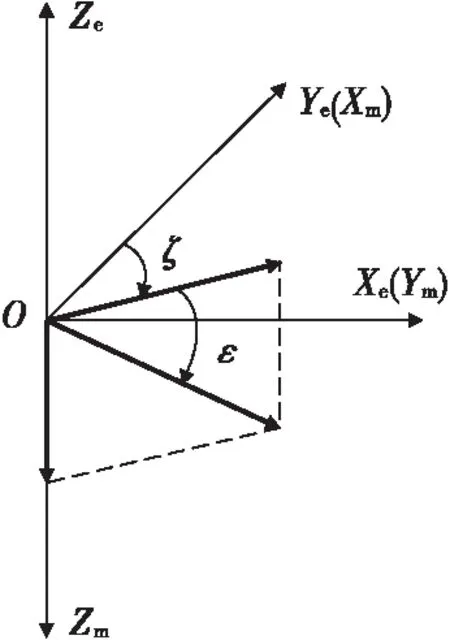
图1 地磁坐标系与地理坐标系Fig.1 Geomagnetic coordinate system and geographic coordinate system

OXeYeZe为地理坐标系，OXe轴沿水平线指向地理东，OYe轴沿水平线指向地理北，OZe轴垂直向上。发射坐标系OXlYlZl的OYl轴与地理坐标系OZe重合，射向ψ为从OYe到OXl转过的角度，北偏东为正。

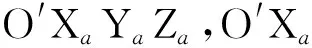
图2 弹体坐标系与地理坐标系Fig.2 Bullet coordinate system and geographical coordinate system

2 地磁场畸变方向测量方法

地磁场可近似视为匀强场，铁磁性物体在地磁场中会使得周围原有匀强场发生畸变，即改变原有的磁场矢量。如图3所示，在弹丸远离目标的区域，目标的铁磁性物质对地磁场的扰动十分微小，可忽略不计，在此阶段基于弹丸发射时的初始条件以及传感器测得的磁场信息，解算弹丸姿态角γ、θ、φ。

图3 铁磁性目标周围地磁场畸变示意图Fig.3 Schematic diagram of geomagnetic field distortion around a ferromagnetic target

弹丸接近目标区域时，在弹丸高速飞行及滚转的情况下，短距离内偏航和俯仰的角度变化可以忽略，因此基于远离目标区域时解算的姿态角度，结合传感器测得磁场的数据产生变化，可以求解此时地理坐标系下的地磁场参数，进而确定磁场矢量的方向。

2.1 磁场方向解算模型

根据前述坐标系定义及图1、图2，可以将地磁场矢量H在地理坐标系下表示为

(1)

弹体坐标系下的任意磁场矢量可通过坐标系变换，在地理系下由磁场强度、磁倾角及磁偏角表示。

(2)

式(2)中，γ、θ、φ为弹丸的滚转、俯仰、偏航三个姿态角，ψ为弹丸射角，如图2所示。

用A、B、C、D表示等式右边的四个三阶矩阵即

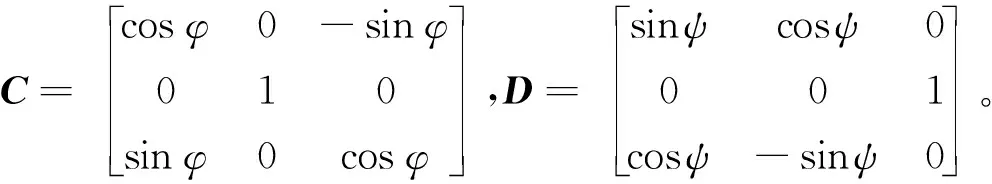
易知A、B、C、D均为三阶可逆矩阵，则

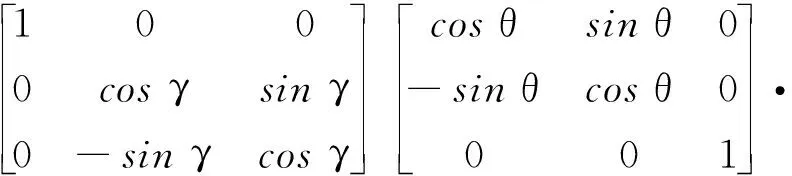
(3)

式(3)也为三阶可逆矩阵，故可将式(2)简化为

Hb=FHe，

作矩阵变换得

He=F-1Hb，

(4)

即可建立如式(5)所示地理坐标系下磁场矢量和弹体坐标系下磁场三分量的关系：

(5)

基于弹体坐标系下磁场三分量数据，可以得到地理坐标系下磁场强度H、磁倾角ε和磁偏角ζ，进而确定磁场矢量的方向。

2.2 含有传感器误差的磁场方向解算模型

2.2.1传感器误差因素

在对磁场仿真的过程中，由于数据信息用于模拟传感器测量分量，因此对于仿真可靠性的误差影响因素主要考虑来自于传感器误差，本文主要考虑传感器三轴正交性误差、三轴灵敏度误差以及传感器零偏误差。基于仿真数据，作定性、定量误差输入，分析讨论不同因素对于磁场方向测量的影响效果。

灵敏度误差是由于地磁传感器三个敏感轴之间的灵敏度和模拟电路放大增益不一致而引起的误差。

偏置误差即零偏误差，是由于地磁传感器和模拟电路的零位实际并不为零而引起的误差。

非正交误差是由于地磁传感器三个敏感轴的实际方向不完全正交而引起的误差。

如图4所示，坐标系原点O为地磁传感器的中心，OXsYsZs为地磁传感器的传感器坐标系(正交坐标系)，三个坐标系方向为地磁传感器的理想敏感轴方向，OXnYnZn为地磁传感器的敏感轴坐标系(非正交坐标系)，三个坐标系方向为地磁传感器的实际敏感轴方向。假设OYsZs与OYnZn位于同一平面内且平行于传感器底面，OZs与OZn重合。α为OXn与OXs的夹角，δ1、δ2和δ3为地磁传感器的三个非正交误差角，其中δ1为OYn与OYs的夹角，δ2为OXn与OYs的夹角，δ3为OXn与OZs的夹角[8]。

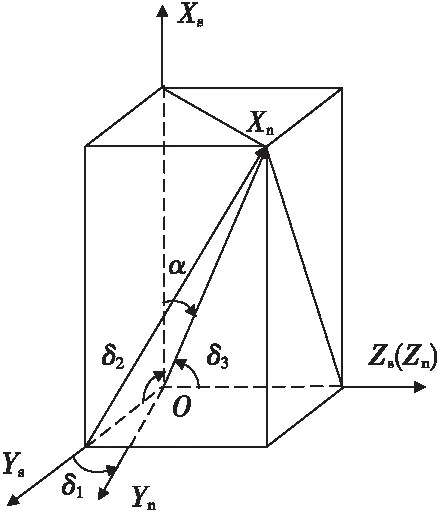
图4 地磁传感器坐标系Fig.4 Geomagnetic sensor coordinate system

2.2.2误差模型

灵敏度误差用矩阵形式表示为

(6)

式(6)中，Pis表示灵敏度误差矩阵，six、siy和siz分别表示地磁传感器三个敏感轴的灵敏度误差系数。

偏置误差用矢量形式表示为

(7)

式(7)中，bi表示偏置误差矢量，bix、biy和biz分别表示传感器三个敏感轴的偏置误差系数。

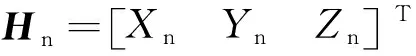
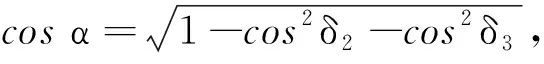
Hn=PioHs，

(8)

为非正交误差矩阵。

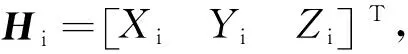
Hi=PisHn+bi=PisPioHs+bi，

(9)

式(9)即为地磁传感器自身误差模型。

故结合式(4)可得，含有传感器误差的磁场方向解算模型为

He=F-1Hb=F-1Hi=F-1(PisHn+bi)=
F-1(PisPioHs+bi)。

(10)

2.2.3误差校正模型

由于地磁传感器的灵敏度误差矩阵Pis和非正交误差矩阵Pio均为非奇异矩阵，存在逆矩阵，根据式(10)可计算真实的地磁场矢量：

Hs=Pi(FHe-bi)，

(11)

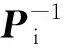
式(11)即为地磁传感器的自身误差校正模型。在自身误差的影响下，地磁传感器输出的地磁场矢量位于一个椭球面上，并且椭球方程的系数是地磁传感器9个自身误差系数的函数，以椭球拟合求得9个误差系数，可实现地磁传感器的自身误差校正[8-9]。

3 测量原理仿真验证

3.1 静态磁场仿真

本文以简单铁磁性物体模型为研究对象，利用Ansys Maxwell软件进行静磁场仿真，探究地磁场中铁磁性目标周围畸变磁场的方向变化。

首先建立仿真模型。通过对各类简单外形模型进行磁场仿真发现，在相同软磁性材料、相同磁场环境激励下，不同形状的简单目标对于磁场的扰动规律相似，因此本文中为简化仿真条件，采用立方体模型进行仿真分析。另外，铁磁性目标对地磁场的扰动特性不仅与其在地磁场中的方向位置有关，还与目标的大小尺寸以及材料特性有关。

选取模型尺寸为100 mm×100 mm×100 mm的立方体，模型材料选择常见的软磁材料45钢，其在地磁环境下的相对磁导率约为200。

设置好模型材料特性后再依次进行边界设置、添加激励、确定求解步，最后对目标进行求解分析。仿真时所加激励磁场强度He大小为43 A/m，由公式Be=μ0·He(μ0=4π×10-7T·m/A，真空磁导率)，可得磁感应强度Be大小约为54 000 nT，方向与XOY平面平行，指向Y轴正方向。求解区域设置为真空，范围为X(-500,500)，Y(-500,500)，Z(-500,500)(单位：mm)。

在YOZ平面上的求解域内得到磁场畸变方向示意图及磁感应强度云图如图5所示，可以看到在铁磁性目标附近会产生明显的磁场畸变，而在远离目标区域磁场为匀强磁场。

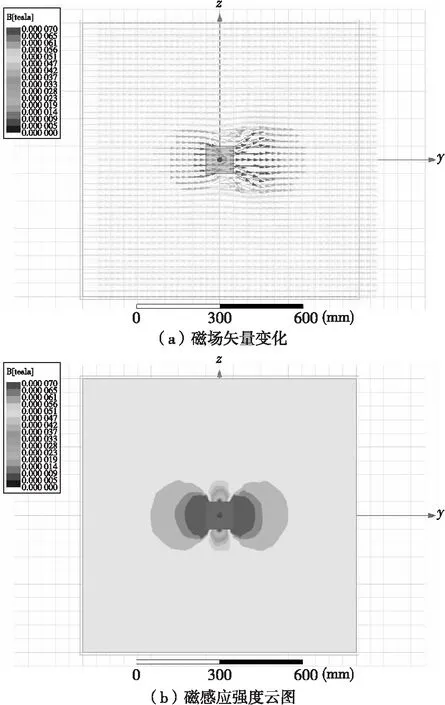
图5 磁场畸变示意图Fig.5 Schematic diagram of magnetic field distortion

取平行于Y轴的直线轨迹Line1，坐标范围为Y(-400,400)，使用Fields Calculator提取轨迹上磁化感应强度在三个坐标轴上的分量，进一步运算得到该直线轨迹上磁场矢量在坐标系下的磁倾角、磁偏角及磁感应强度标量值，并以0.5 mm为步长导出数据文本。

3.2 磁场方向解算

假设弹丸以200 m/s的飞行速度以及2 r/s的角速度作匀速飞行及匀速转动，对仿真得到的磁场数据作简单处理。在静磁场中的直线轨迹已知，则弹丸三个姿态角及发射角也已知，满足式(5)求解要求，结合磁场矢量在坐标系三个坐标轴上的分量数据，可以解得地理坐标系下磁倾角、磁偏角和磁场强度的变化，从而确定轨迹上磁场的方向变化。

将提取的磁场三分量数据作为磁场方向解算的输入值，在Matlab中进行求解，与图6所示以Maxwell中Fields Calculator计算得到的角度值进行比较，证明前述磁场方向解算原理可行。

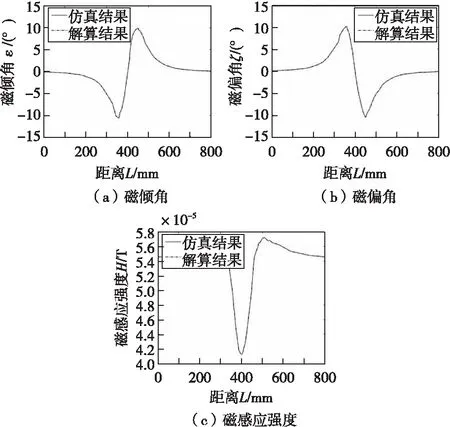
图6 模型解算结果与磁场仿真数据对比Fig.6 Comparison of model solution results and magnetic field simulation data

从图6中可以看出在100～600 mm范围内磁场的三分量以及强度有明显变化，可近似视为磁场畸变区域，磁倾角和磁偏角的变化范围约为±10°，磁感应强度变化范围约为15 μT。

在实际弹丸运动情况下，可在发射后且远离目标区域范围内，以传感器测得的地磁数据求得弹丸姿态角，由于弹丸在短路径范围内的偏航及俯仰角度变化可近似视为不变，故在远离目标区域求得的姿态角可作为靠近目标区域时的初始已知量，对磁场方向变化进行求解，此处对远离至靠近目标的判断依据还有待进一步研究讨论。

3.3 传感器自身误差对磁场方向解算的影响

假设地磁传感器的3个灵敏度误差系数分别为six=1.005、siy=0.996和siz=1.003，3个偏置误差系数分别为bix=900 nT、biy=850 nT和biz=770 nT，3个非正交误差角分别为δ1=1°、δ2=89.5°和δ3=89°。基于前述误差模型式(9)得到误差数据，在当前仿真条件设定下，利用式(10)解算磁场角度及磁感应强度，各项误差对于磁场方向解算结果的影响如图7所示。

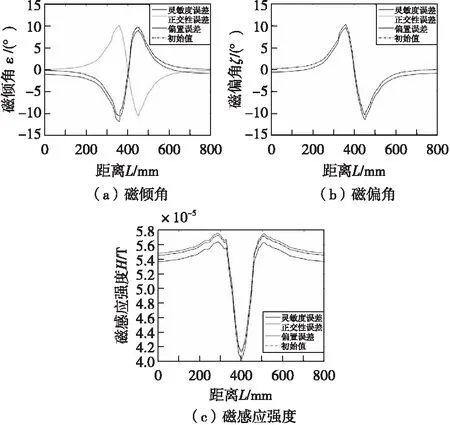
图7 三轴磁传感器误差对各参数解算的影响Fig.7 Effect of triaxial magnetic sensor error on the solution of each parameter

可以得到磁传感器的灵敏度误差对磁场特征信息的影响主要在于磁场强度，但与其他误差因素相比，对方向测量结果的影响很小；传感器的正交性误差对磁倾角和磁场强度的解算影响较大，对磁偏角影响较小；传感器偏置误差对磁感应强度影响较小，主要影响磁场方向角度的解算。

基于椭球拟合的误差补偿方法[8-9]，对前述传感器误差模型进行补偿校正，得到结果如图8所示，误差校正效果理想，有效提高了磁场方向测量精度。

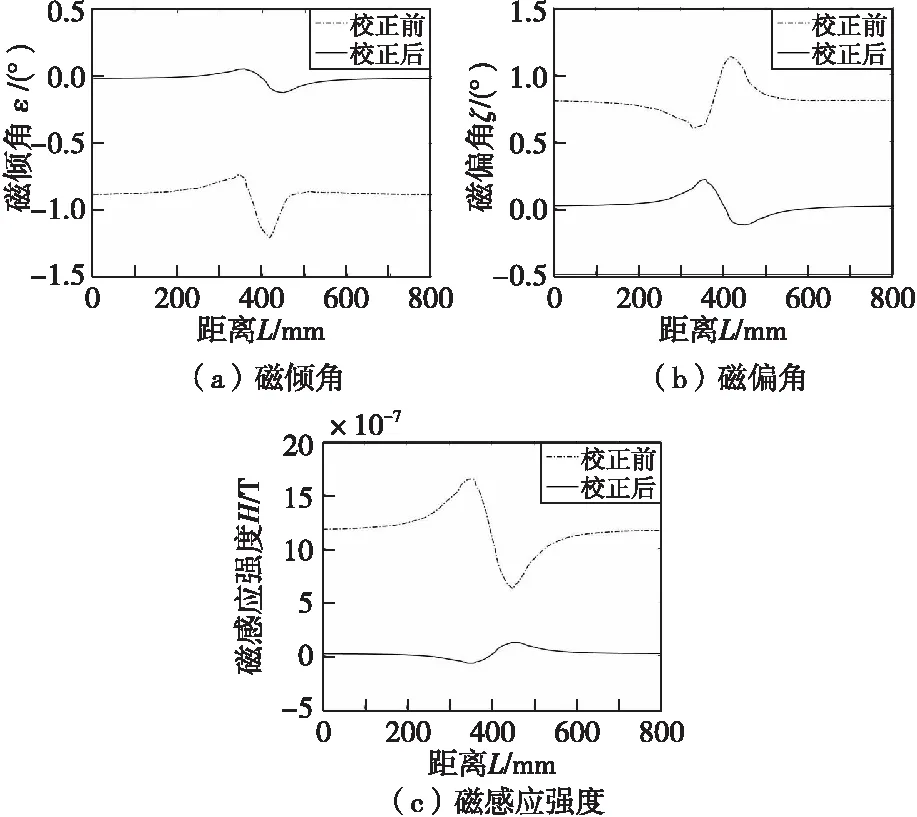
图8 传感器误差校正前后的各参数解算差值Fig.8 Difference in the solution of each parameter before and after sensor error correction

4 结论

本文通过建立以磁倾角、磁偏角及磁场强度为参数的磁场方向解算数学模型，结合地磁传感器对磁场的测量以及弹丸姿态角数据，实现对地磁场中铁磁性目标物体周围畸变磁场的方向变化解算，为目标定位提供依据。以Maxwell软件实现地磁场中铁磁性物体周围磁场畸变特征的静态磁场仿真，利用仿真数据验证磁场方向解算模型的可行性，同时对提取弹载磁传感器测量数据时的误差因素进行分析讨论，作误差校正后的结果与原始值相比，提高了解算精度。

本文建立的仿真模型与实际的空中铁磁性目标相比有很大程度的简化，对于弹丸靠近目标的轨迹选择有一定特殊性，考虑及分析到的误差因素有限。在实际问题中，铁磁性目标物体对磁场扰动的复杂程度仍有待深入研究分析，实际弹丸运动中由于自身章动或环境干扰等因素影响，会造成运动轨迹的偏离，因此对于复杂运动条件下的诸多因素还需进一步加以考虑，从而完善磁场方向解算模型，拓展其适用性。