基于侵彻过载信号应力波补偿的靶后精确起爆控制技术

马孟新，牛兰杰,2，李 蓉，孙亚杰

(1.西安机电信息技术研究所，陕西 西安 710065；2.机电动态控制重点试验室，陕西 西安 710065)

0 引言

侵彻战斗部打击大厚度目标时，通过引信中加速度传感器识别过载，确定侵彻战斗部侵出靶标后距离，输出爆轰能量，毁伤坚固防护下的高价值目标。侵彻过程，引信中加速度传感器识别到的过载信号振荡严重，碰靶及出靶等目标特征不易识别，严重影响靶后起爆控制精度。随着攻防矛盾加剧，侵彻着速不断提高，过载信号振荡程度日趋严重。

目前国内针对此问题一般采用低通滤波[1-4]、匹配滤波、机械滤波[5]、伪自相关[6]等方式，取得了一定成果，但都没有充分利用过载信号粘连的内在机理，所以其适应性难以评价[1]。

通过理论分析，加速度传感器识别到的侵彻过载信号包含四部分：弹体刚体过载、应力波、弹引连接结构响应及内外部噪声。其中刚体过载体现侵彻目标特征，刚体过载上升表明弹体在碰靶和开坑阶段，刚体过载平稳表明弹体在稳定贯穿阶段，刚体过载下降表明弹体在出靶阶段，弹体在碰靶强动载激励下产生应力波[7]。

基于机械振动理论，形成弹体刚体运动与轴向振动相结合的侵彻垂直靶板作用模型，当战斗部作为一个自动控制系统响应弹靶应力时，振动响应过载信号的能量主要集中在一阶轴向振动固有频率附近，当靶体响应力中的高频与战斗部某阶轴向振动固有频率相近时，战斗部会发生明显的谐振现象，导致振动响应过载大幅增加，是目标特征被淹没的主要因素[8-10]。为消除应力波信号对目标特征的影响，利用计算或仿真的方法得出应力波的先验信息，采用补偿的方法将过载信号抖动消除，凸显刚体过载，提高碰靶和出靶等目标时刻及余速，最终达到提高起爆控制精度的效果。

1 侵彻过程弹体动力学模型

为揭示侵彻过程中传感器的动态响应机理，将机械振动理论引入侵彻过程理论分析和计算，给出一种简化的侵彻战斗部-引信系统动力学模型[11]。

该模型描述了战斗部垂直侵彻均质混凝土靶板的理想工况。在该工况下，战斗部在靶板内弹道稳定，战斗部卵形部各向受力均匀，受力面和受力方向不随侵彻历程发生变化。

以侵彻战斗部-引信系统的载荷传递关系为基础，基于单自由度弹簧-质量-阻尼系统建立的动力学微分方程，通过谐响应分析确定固有频率等动力学参数[8]。

1.1 刚体运动模型

分析垂直侵彻理想状态，将弹体看成一维细长杆，只考虑纵波对轴向过载信号的影响，忽略横波及曲面波等更加复杂的形式，简化计算模型。

侵彻过程中，弹靶作用力使弹体做减速运动，可简化为质心的刚体运动。假设弹体的位移为x1，根据牛顿第二定律得到刚体运动方程为

(1)

式(1)中，t为侵彻时间，M为战斗部质量，Fx为战斗部受到的弹靶作用力。

1.2 应力波传播模型

针对弹体内应力波的传播，采用振动模型进行分析。假设战斗部为两端自由的一维圆杆，可根据应力波传播理论计算出弹体一阶轴向振动的固有频率f1，理论值为

(2)

式(2)中，L为战斗部长度，E0为战斗部壳体材料的弹性模量，ρ为战斗部壳体材料的密度。

由于真实战斗部与理想的一维圆杆有差异，通过仿真及对等效的一维圆杆计算，分别得出固有频率，结合大量实测数据的谱分析，对式(2)进行修正，可近似为

(3)

式(3)中，k一般取0.8～1.2。

在战斗部一阶轴向振动频率已知后，借鉴机械振动理论进行战斗部应力波传播模型建模。

将战斗部等效为具有阻尼特性的弹簧，质量集中于战斗部尾部，则一阶轴向振动模型可简化为单自由度弹簧-质量-阻尼系统，如图1所示，与基础运动引起的强迫振动类似。

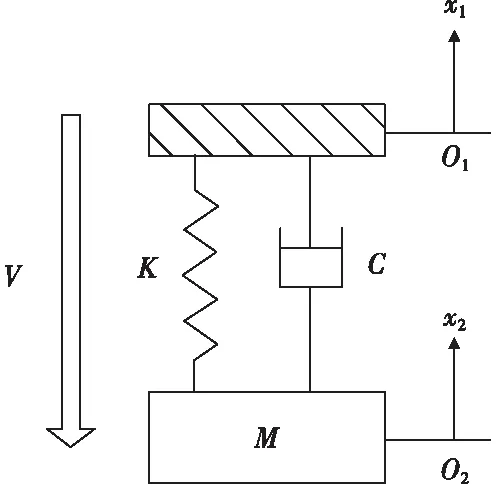
图1 战斗部等效的单自由度弹簧-质量-阻尼系统Fig.1 Equivalent unidirection spring-mass-damping system of warhead

图1中，战斗部头部位移为x1，与刚体运动一致，战斗部尾部(即引信安装位置)位移为x2，战斗部等效刚度K与等效阻尼C分别如下式所示：

(4)

(5)

式(4)、式(5)中，ω1称为无阻尼自然频率，为f1对应的圆周固有频率，单位为rad/s，ξ为无量纲阻系数。

根据图1可知，弹靶作用力经弹簧传递后再作用于战斗部，此时战斗部受两部分力：一是阻尼力，其方向与振动方向相反，大小与振动速度成正比；二是弹簧力，其方向与振动方向相反，大小与振动位移成正比。由于战斗部尾部对于头部相对位移x2-x1，因而作用于战斗部的弹簧力为K(x1-x2)，阻尼力为C(dx1-dx2)/dt。

以战斗部为研究对象可得到运动微分方程：

(6)

(7)

记战斗部一阶轴向振动引起的长度变化量为ΔL，则ΔL=x2-x1，当ΔL>0时，战斗部被压缩，反之被拉伸。此时式(7)可简化为式(8)，即一阶轴向振动模型，描述了战斗部轴向振动变形与弹靶作用力之间的关系。

(8)

将式(8)进行拉普拉斯变换，可得到以刚体过载为输入，以弹性过载为输出的传递函数：

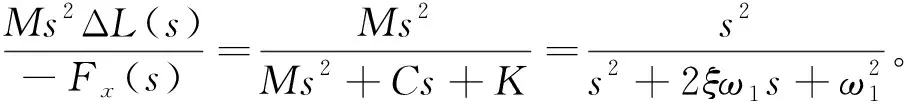
(9)

可以将G(s)的分母进行因式分解后，得到

(10)

对于金属而言，ξ为无量纲阻尼系数，远小于1，所以系统的冲击响应为

h(t)=M(eat-ebt)u(t)，

(11)

2 应力波补偿及起爆控制算法

2.1 仿真模型及工况

为了保证本应力波补偿方法的有效性，首先说明仿真及归纳总结过程采用模型的准确性。

本文采用有限元仿真软件Ansys/LS-Dyna完成侵彻过程仿真。在保证仿真精度和计算效率的前提下，尽量还原产品真实状态。

对重要的加载部件(弹体)、起重要连接作用及载荷传递的部件不可失真地进行简化。对关注点(引信体)力学载荷几乎没有影响的细小零部件(小螺栓、小销钉、小弹簧垫片，部件上的小孔等)及微小特征(倒角、棱、退刀槽等)等简化或删除。

经过前期仿真积累，得到了大量有效的仿真经验，兼顾精度和效率，获得不同外形、材料、尺度及结构的建模策略，包括材料模型及参数、接触方式、网格划分等。网络划分如图2所示。

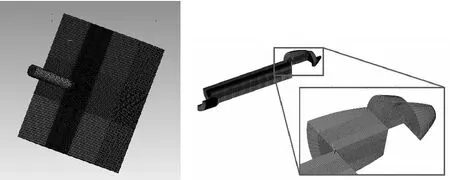
图2 侵彻工况和弹体的网格划分Fig.2 Meshing of penetration condition and warhead

通过仿真数据和实测数据的对比验证仿真模型的有效性。本文仿真采用的战斗部长度为980 mm，战斗部壳体的材料密度为7 850 kg/m3，杨式模量211 GPa。实测数据为该战斗部以800 m/s速度侵彻300 mm厚靶板采集到加速度传感器识别到的信号。仿真工况和实测工况一致。

图3为实测数据和实测数据的频谱，从图中得出应力波特征频率为2 827 Hz。图4为相应的仿真数据及频谱，特征频率为2 994 Hz，误差为5.9%。同时可以看出实测信号有比较丰富的高频分量，这些高频分量是由于传感器及电路采集过载信号时引入噪声引起的，而仿真数据只包含侵彻过程的刚体过载及应力波，所以在高频部分存在一定的差异。但对于本文讨论的范围，仿真精度满足要求，足以支撑应力波信号特征的提取及补偿算法实现。

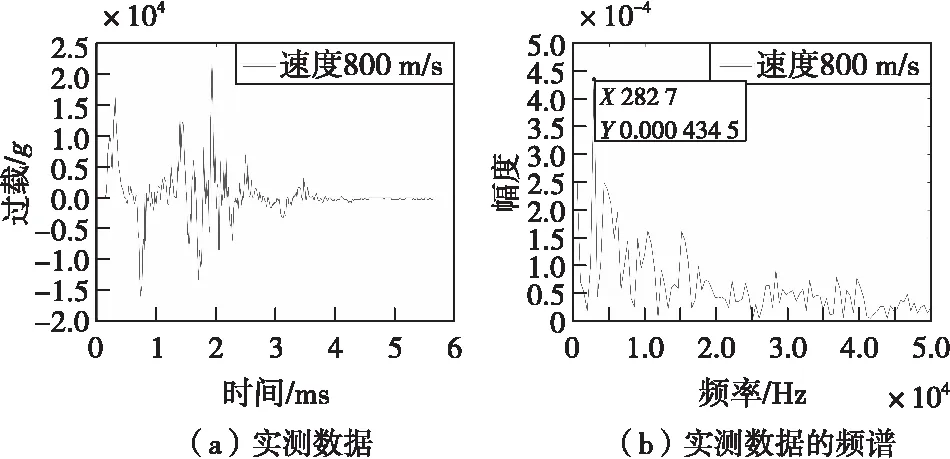
图3 实测数据及频谱Fig.3 Test signal and spectrum

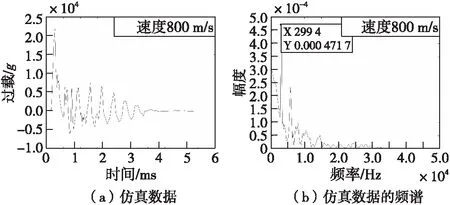
图4 仿真数据及频谱Fig.4 Simulation signal and spectrum

2.2 应力波特征频率确定

在战斗部及侵彻条件确定的情况下应力波的频率和幅值范围是确定的。在完成侵彻战斗部试制前后，分别可采用计算、动态仿真、模态仿真及实测的方法，获得应力波的响应频率和幅值。

针对2.1节战斗部状态，计算得到应力波的特征频率为2 645 Hz，可以将该值作为应力波的理想特征频率。由于此计算过程是将战斗部等效为均匀长直杆，所以理论计算存在一定误差，通过对战斗部建模，将战斗部外形及装药材料完全还原产品真实状态，动力学仿真后进行模态分析，得到更加精确的应力波特征频率，对理论值修正。

如具备条件，可以基于霍普金斯杆原理采用实测的方式对战斗部实物引信部位的信号进行测试，并完成谱分析得到应力波特征频率。采用该方式对仿真和理论计算值进行修正，得到修正因子，根据对大量修正因子的梳理，逐渐固化修正因子的范围，以备后续不具备实物测试的状态使用。

2.2.1侵彻着速对应力波频率的影响

首先验证在相同靶板情况下，不同侵彻着速对应力波特征频率的影响，分别完成了战斗部以300、400、500、600、700、800 m/s侵彻C40强度300 mm厚度靶板的动态仿真，得到引信部位的侵彻过载信号，并对过载信号进行谱分析，侵彻过载信号如图5(a)所示，信号频谱如图5(b)所示，应力波特征频率一致，均为2 930 Hz，说明应力波特征频率和侵彻着速无关。

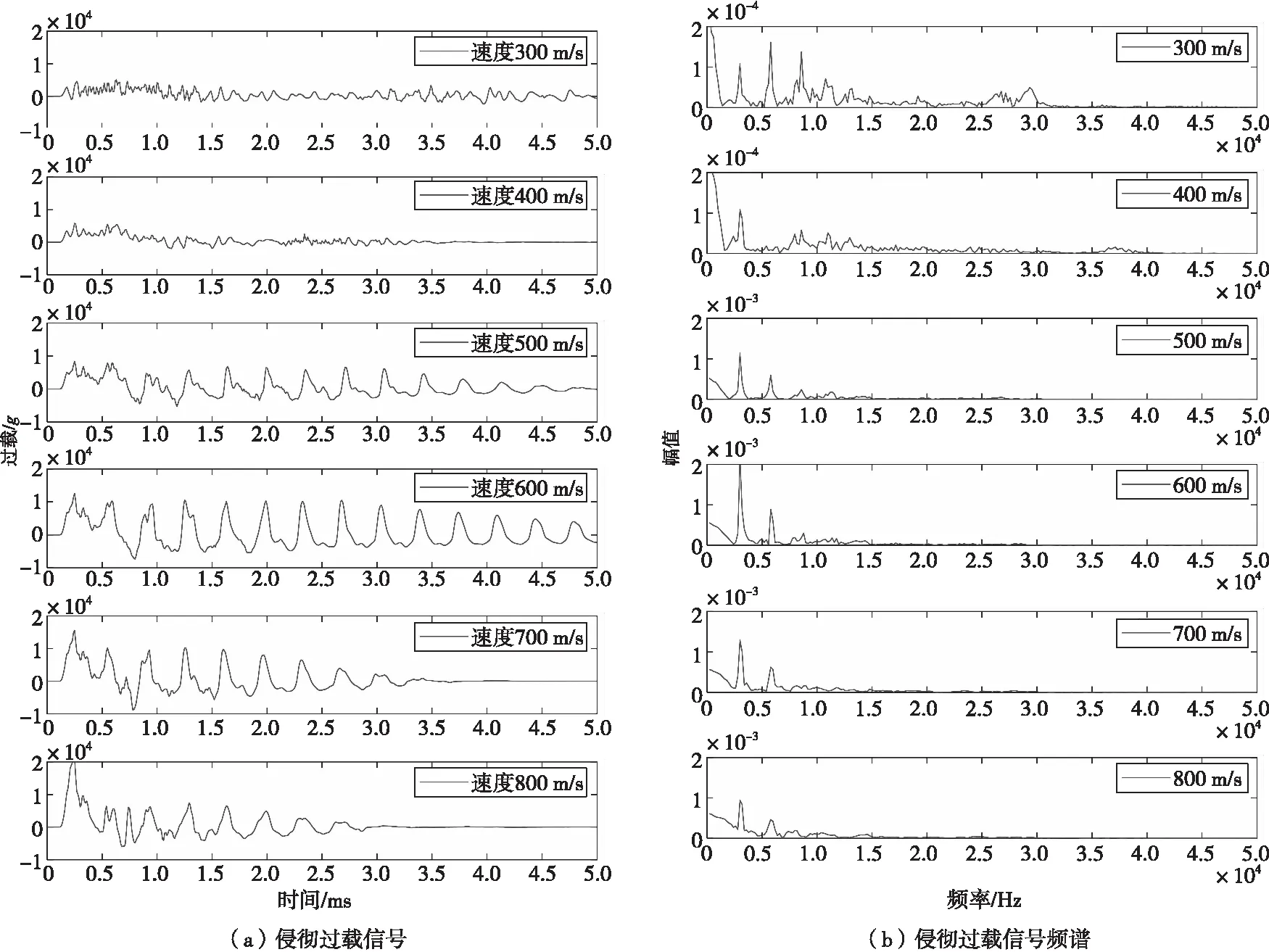
图5 不同侵彻着速的侵彻过载及频谱Fig.5 Penetration signal and spectrum of variant velocity

该值和理论计算值存在差异，确定该种状态修正因子k为1.107，主要是战斗部的卵形部及内部装药结构和圆柱体均匀杆存在差异导致。

2.2.2靶板强度对应力波频率的影响

验证特定速度及特定靶板厚度情况下不同靶板强度对应力波特征频率是否存在影响。完成以500 m/s速度侵彻强度为C35、C40、C45、C50，300 mm厚混凝土侵彻仿真验证，过载信号和频谱如图6所示，经过仿真应力波的特征频率均为2 930 Hz，不随靶板强度发生变化。

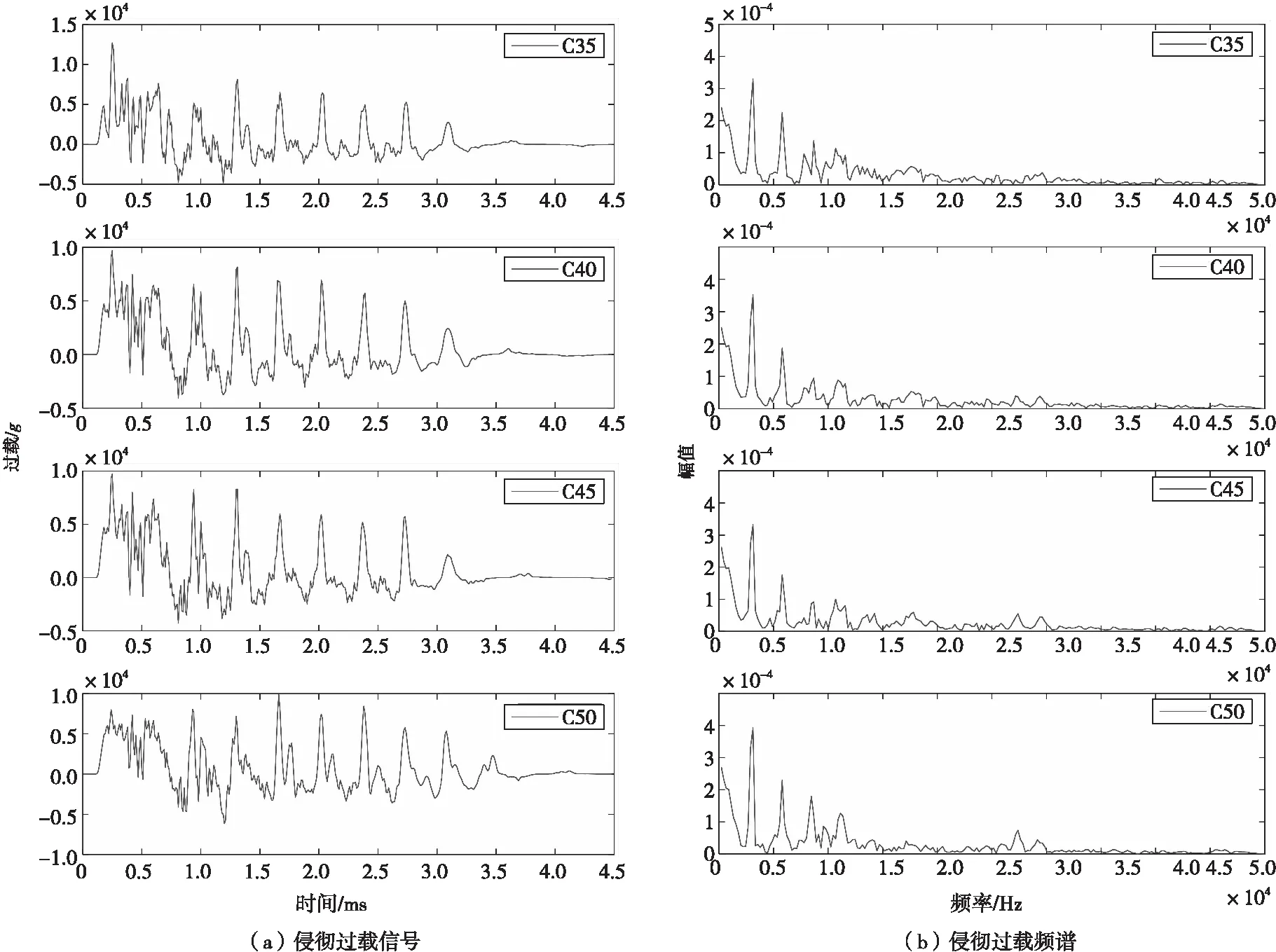
图6 不同靶板强度的侵彻过载及频谱Fig.6 Penetration signal and spectrum of variant compressive strength of target board

2.2.3靶板厚度对应力波频率的影响

验证特定速度下不同靶板厚度对侵彻特征频率的影响。完成100、300、500、1 000、2 000和3 000 mm厚靶板六组数据仿真，图7为过载信号和对应的频谱。经过仿真验证，随着侵彻靶板厚度的增加，应力波特征频率不随靶板厚度发生变化。

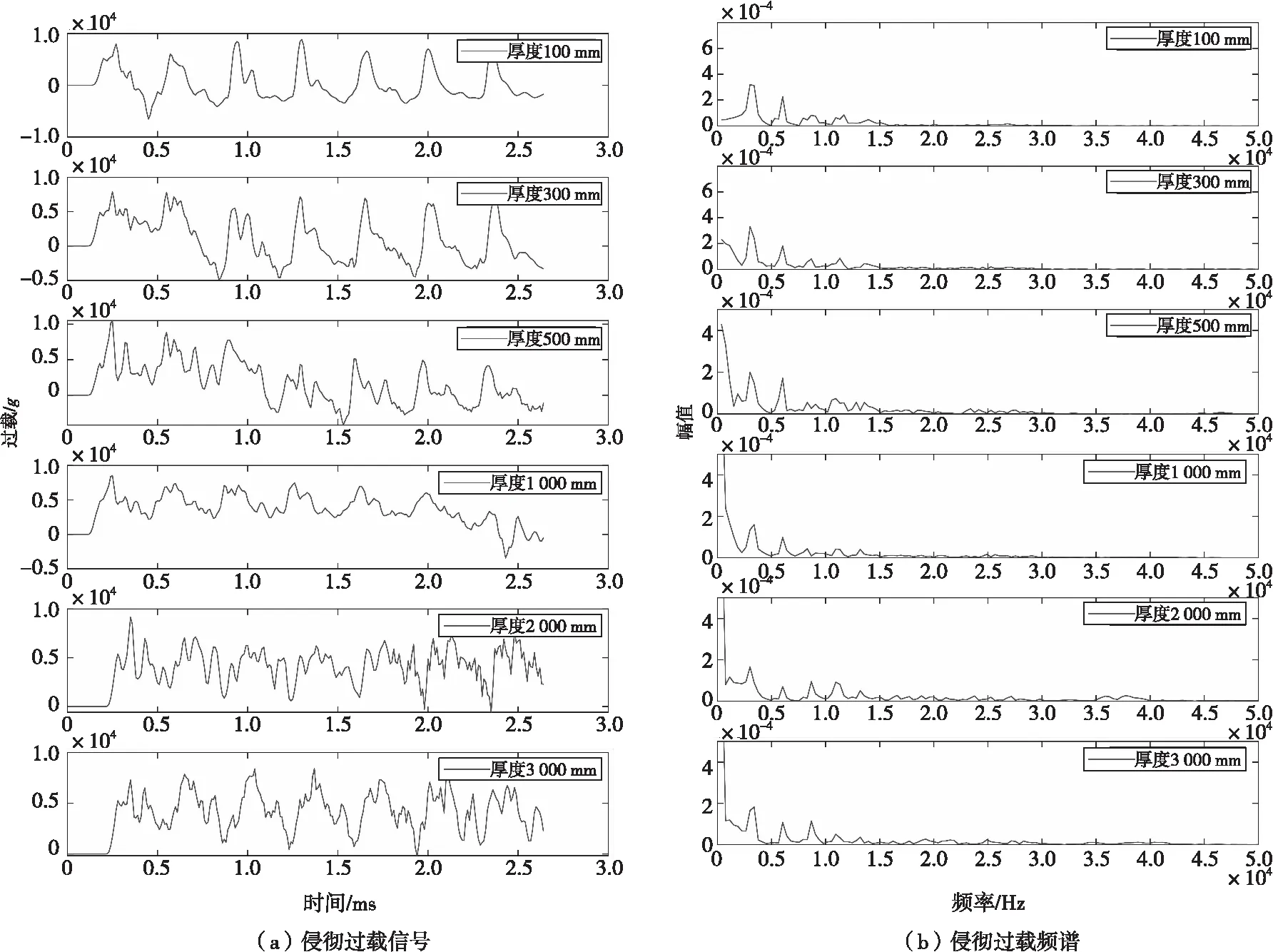
图7 不同靶板厚度的侵彻过载及频谱Fig.7 Penetration signal and spectrum of variant thickness of target board

2.3 应力波幅值范围确定

应力波幅度的先验信息在补偿算法中非常重要，经过初步分析，在战斗部确定的情况下，侵彻着速和靶板强度可能会影响应力波幅度，进行分别验证。

以侵彻180 mm厚的C35强度混凝土工况验证侵彻着速的影响。侵彻着速采用300、400、500、600、700、800 m/s。仿真结果如图8、图9所示，图8为刚体过载，图9为引信部位过载。

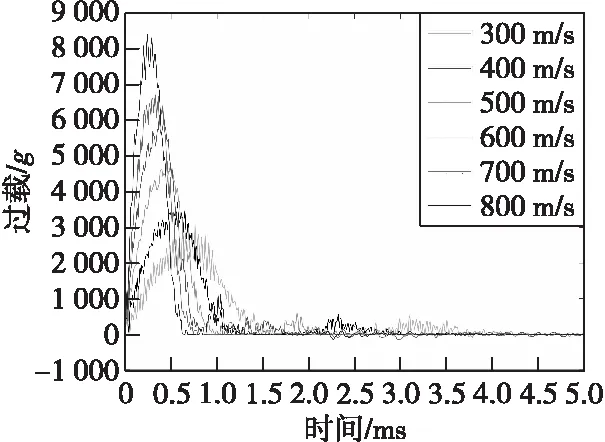
图8 不同速度侵彻C40强度靶板刚体过载Fig.8 Rigid body penetration signal of variant velocity in C40 target board

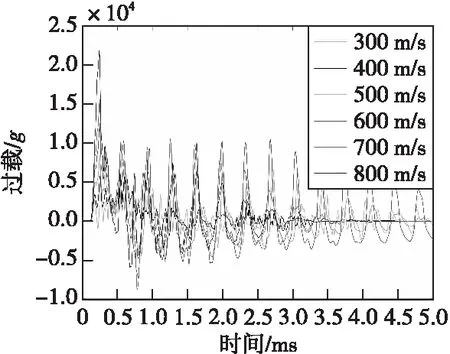
图9 不同速度侵彻C40强度靶板引信部位过载Fig.9 Fuze penetration signal of variant velocity in C40 target board

仿真工况设置引信和弹体之间采用绑定接触，简化引信螺纹连接，避免弹引复杂连接结构对应力波信号的影响。应力波被刚体过载激发，但当刚体过载完全消失时，应力波信号会持续一段时间，可以看出，应力波的幅值和侵彻着速关系明显，侵彻着速越高，应力波幅值越大。

分析靶板强度对应力波幅值的影响，完成战斗部对C35、C40、C45、C50强度侵彻仿真，图10是弹体刚体过载，图11是引信部位过载。在刚体过载为0的时间段，引信部位的过载为应力波成分，从图11中看出应力波的幅值几乎不随靶板强度变化而变化。

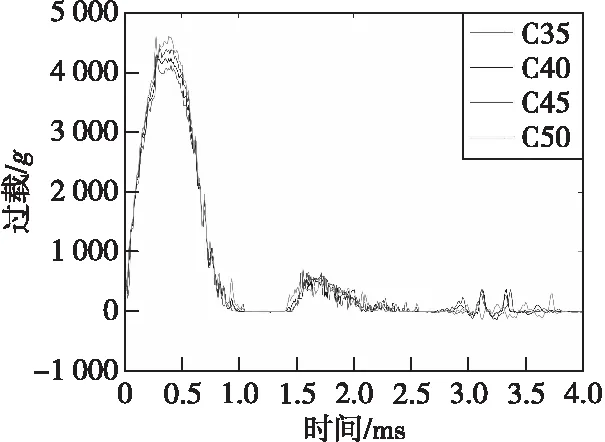
图10 500 m/s速度侵彻不同强度靶板刚体过载Fig.10 Rigid body penetration signal of variant compressive strength of target board in 500 m/s

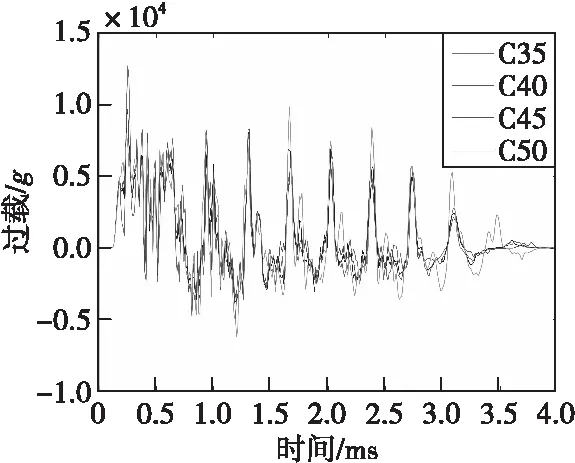
图11 500 m/s速度侵彻不同强度靶板引信部位过载Fig.11 Fuze penetration signal of variant compressive strength of target board in 500 m/s

同时由式(9)可以得出，在战斗部确定的情况下，由于被激发应力波的幅值是输入弹体刚体过载的函数，所以在刚体过载幅值基本不变情况下，应力波幅值不变。

2.4 应力波补偿实现

根据上述理论及仿真分析，在战斗部垂直侵彻均质混凝土靶板工况下，应力波的频率仅为战斗部状态的函数，和侵彻着速、靶板强度、靶板厚度无关。应力波的幅值在战斗部确定情况下仅是战斗部着速的函数。

本文提出的应力波补偿侵彻过载信号靶后精确起爆控制算法的流程如图12所示。

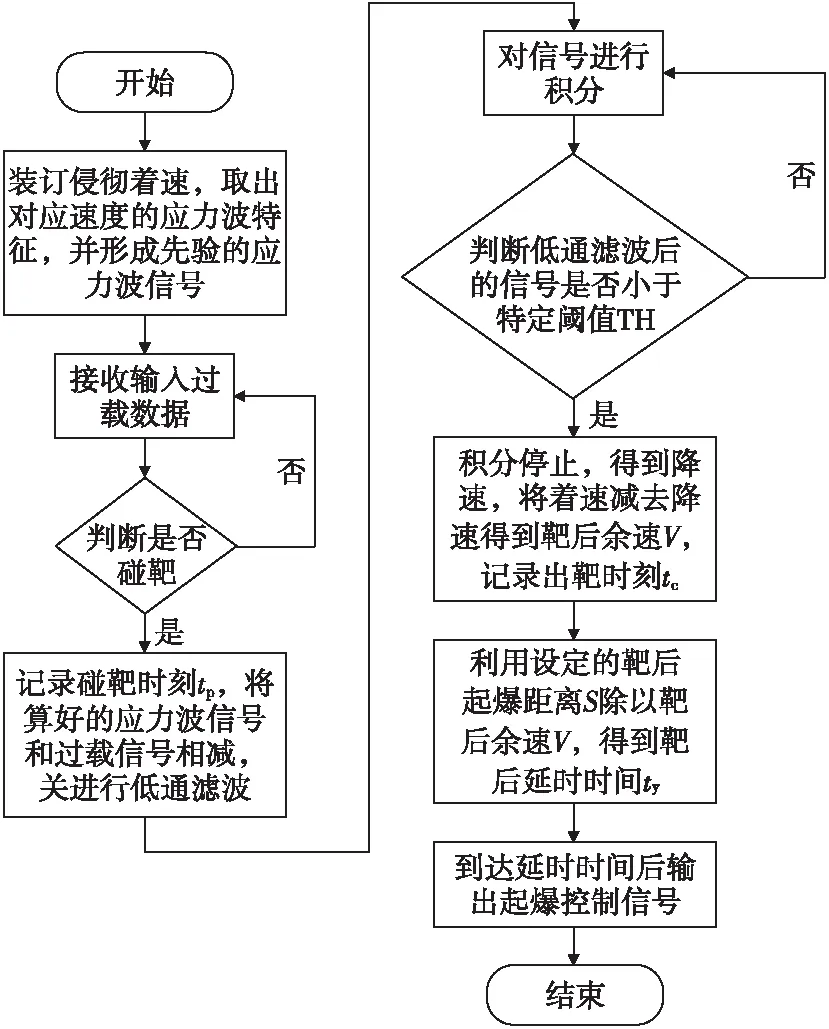
图12 应力波补偿靶后精确起爆控制算法Fig.12 Algorithm of using stress wave to compensate penetration acceleration signal

对于算法中使用的应力波特征频率，采用2.2节方法进行计算并修正后确定。对于应力波被激发后的每一个峰值，因为是侵彻着速的函数，所以完成300～800 m/s速度范围内的侵彻仿真，得到数据如图13所示。形成以速度和应力波峰值为坐标的矩阵(以下简称峰值矩阵)。由于该矩阵需存入起爆控制算法，所以应根据MCU的硬件资源和弹上计算机能提供侵彻着速的精度确定该数据的步长，经分析，该数据步长的合理范围为10～50 m/s。

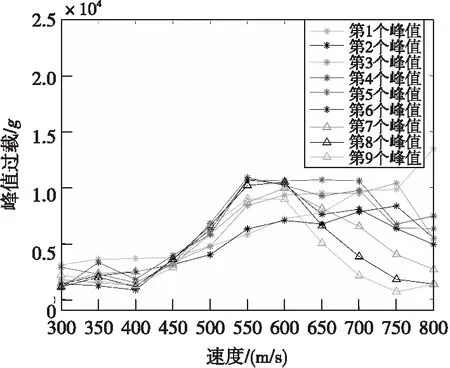
图13 不同速度应力波峰值Fig.13 Peaks of stress wave in variant velocity

本部分给出的数据以50 m/s为步长，并进行线形拟合，对拟合出的曲线观察发现除第1层峰值以外，其他层峰值均随速度先增大后减小。

图14给出570 m/s侵彻着速，通过线形插值得到的各峰值数据。

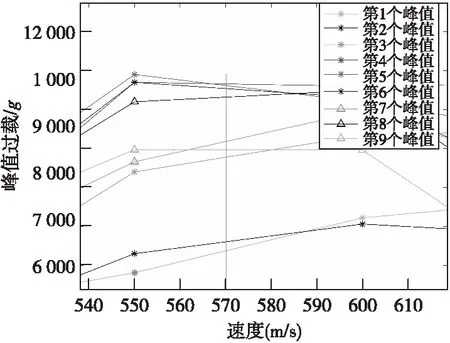
图14 侵彻着速570 m/s对应的应力波峰值Fig.14 Peaks of stress wave in 570m/s

3 仿真验证

通过两组数据完成算法有效性验证。侵彻工况中的侵彻着速、靶板强度、厚度从2.2节分析覆盖的范围中选取。仿真验证采用战斗部侵彻单层厚目标。1) 工况1：侵彻着速600 m/s，靶标强度C40，厚度1 m；2) 工况2：侵彻着速800 m/s，靶板强度C40，厚度2 m。侵彻工况如图15所示。

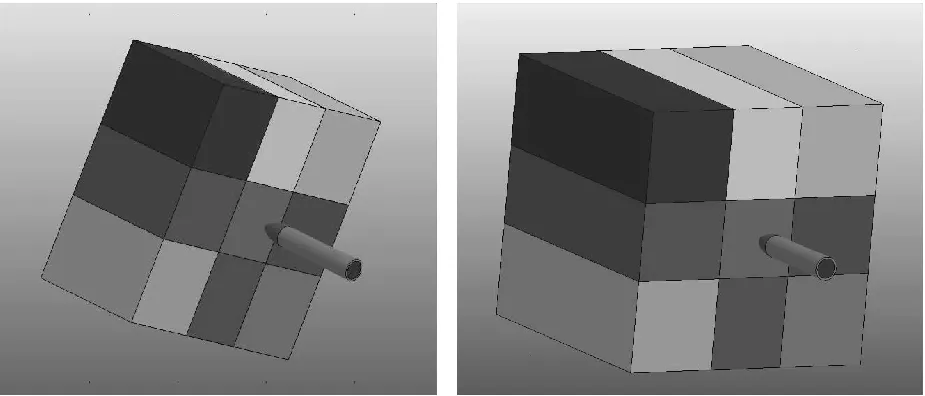
图15 侵彻1 m和2 m靶标仿真工况Fig.15 penetration condition of 1 m and 2 m thickness target board

图16(a)为仿真得出的着速600 m/s侵彻1 m厚靶标的过载曲线。针对仿真工况，得出应力波特征频率为2 990 Hz，根据速度从应力波峰值矩阵中取出的峰值过载为 [7 220,7 060,9 340,10 600,10 200,10 300,9 960,10 500,8 960]g，形成应力波信号，按照算法流程进行处理，得到图16(b)。

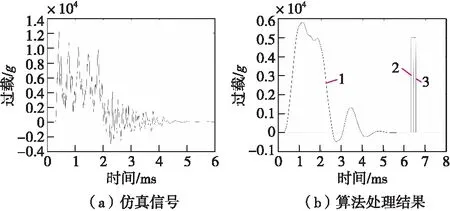
图16 着速600 m/s侵彻1 m厚目标原始信号及算法仿真结果Fig.16 Simuation siganl and result of detonation control method in 600 m/s and 1m

通过设定阈值提取出靶特征，得出侵彻出靶时刻为碰靶后2.4 ms，并通过对曲线积分得到靶内降速为90.4 m/s，这和仿真过程中的2.2 ms延时及92.4 m/s的降速基本吻合，误差分别为9.1%和2.65%。通过着速和降速得到靶后余速为509.6 m/s，如指标要求在靶后2 m起爆，那么在碰靶后延时2/509.6+2.4=6.3 ms输出起爆信号即可满足要求。图16(b)中曲线1为算法处理过后得到的近似刚体过载信号，曲线2为靶后2 m起爆的理论时刻，曲线3为算法运行输出的起爆控制信号，误差为1.9%。

图17(a)为仿真得出的以800 m/s着速侵彻2 m厚靶标的过载曲线，针对仿真工况，得出应力波特征频率为2 990 Hz，根据速度从应力波峰值矩阵中取出的峰值过载为[13 470,5 468,5 452,7 470,6 330,4 910,2 680,1 380,1 340]g，形成应力波信号，按照算法流程进行处理，得到图17(b)。

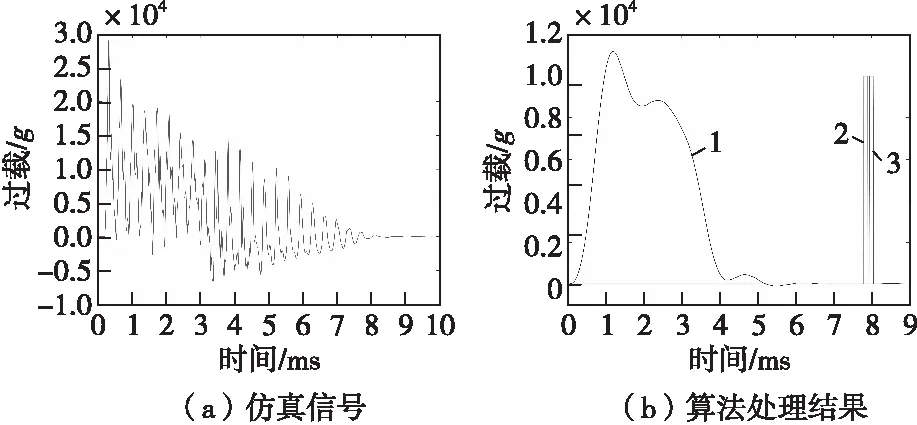
图17 着速600 m/s侵彻2 m厚目标原始信号及算法仿真结果Fig.17 Simuation siganl and result of detonation control method in 600 m/s and 2 m

通过设定阈值提取出靶特征，得出侵彻出靶时刻为碰靶后4.05 ms，并通过对曲线积分得到靶内降速为265 m/s，这和仿真过程中的3.9 ms延时及266 m/s的降速基本吻合，误差分别为3.8%和0.4%。通过着速和降速得到靶后余速为533 m/s，如指标要求在靶后2 m起爆，那么在碰靶后延时2/533+4.05=7.8 ms输出起爆信号即可满足要求。图17(b)中曲线1为算法处理过后得到的近似刚体过载信号，曲线2为靶后2 m起爆的理论时刻，曲线3为算法运行输出的起爆控制信号，误差为2.0%。

4 结论

经过两组仿真数据验证，针对战斗部无攻角垂直侵彻均质混凝土靶板的理想工况,本文提出的采用应力波补偿的大厚度目标靶后精确起爆控制算法能准确识别战斗部出靶时刻，同时得到战斗部出靶余速，进而完成靶后特定位置精确起爆控制的战技指标要求。

针对带有攻角和着角侵彻非均质混凝土靶板的工况，需要考虑战斗部所受应力方向和应力面变化的更加逼近真实状态的模型，是本文后续关注的研究方向。