浅析数形结合在中学数学解题中的应用

魏 苹

(福建省福州江滨中学，福建福州，350015)

社会在高速发展，新时代的科技水平不断推动着我国教育事业前进的步伐.一个崭新的教育理念形成的今天，社会也对学生提出了更高的要求.学生不仅要学好教材中的内容，还要有较高的数学思维能力.数形结合在中学数学中，是一种最直接的教学方式.数学反映着许多实际生活中的数量关系和几何关系，也就是我们口中所说的数和形.他们之间是相互联系，自然也是可以相互转变的.数在概念上解释让人觉得十分抽象，而形则是客观直接体现出来的.可是他们之间又有着十分紧密的联系.数代表着数量，而形代表着直观.那什么是数形结合呢？其概念就是他们之间的确立的关系，通过互相转换来解题的方法.所以，在平时的课堂上，教会学生学会运用数形结合的方法来解决问题，使学生在运用中不断开发数学解题思路，提高对于数学的学习兴趣[1].

1 数形结合在方程与不等式问题中的运用

我们在求解一元一次方程、一元一次不等式、二元一次方程组等的时候，可以在一个平面的直角坐标系里面的一次函数所关联的直线为线索的解法，这样的解法称为图形解法.

1.1 利用数形结合中的图形来解一元一次方程

题1解方程3x-6=0.

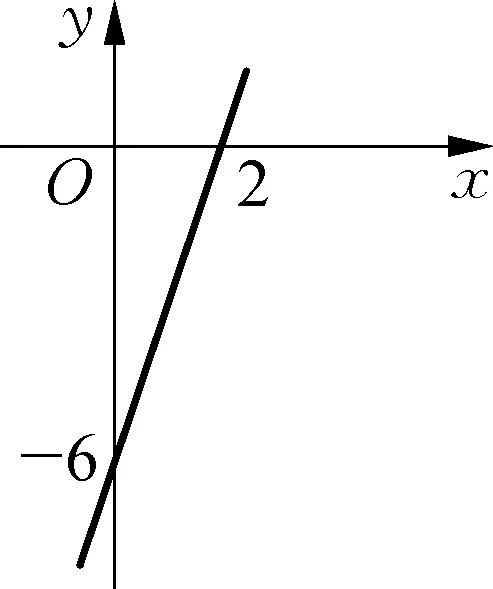
遇到这样的题目，我们可以在坐标系中画出与方程相应的一次函数y=3x-6的图象，函数值y=0的时候也就是图象与x轴相交的点，那这个点就是我们所求的答案.

解：如图，在坐标系中，我们把直线y=3x-6画出来，随后我们观察这幅图，知道直线y=3x-6和x轴相交于点(2，0).因此，3x-6=0的方程解为x=2.

1.2 利用数形结合中的图形来解一元一次不等式

题2解不等式-2x+4<0.

面对一元一次不等式，我们要找出相应的一次函数.那么不等式-2x+4<0相应的一次函数是y=-2x+4.那我们在根据数形结合中的图形来观察，当x等于多少的时候，直线上的点会出现在x轴的下面呢？

解：我们先在坐标系中把y=-2x+4的直线给画出来，随后我们观察这幅图，在x>2的时候，y=-2x+4的点出现在x轴的下面，所以我们从图形上可以得知，不等式-2x+4<0的答案为x>2.

我们用数形结合的思路来解方程与不等式，首先要做出它们对应的一次函数图象，再观察图形就可以得到我们想要的答案.观察图形的办法最能直接体现数形结合的思路.[2]

2 数形结合在有理数问题中的运用

有理数运算中，最基础的题目就是有理数加减，而且这种题目也是在平常习题中十分常见的类型.因此如何掌握用数形结合的思想来解决有理数加减问题，就成了学习的关键.

题3在东西方向的道路上，小猴第一次跳了2 m，第二次跳3 m，这时候小猴处于原来位置的什么方向呢？距离又是多少m呢？

在这道题目中，我们可以得到如下的结论：

A. 小猴朝西第一次跳2 m，再朝西第二次跳3 m，小猴这时候距离原来地方是5 m.

B. 小猴朝东第一次跳2 m，再朝东第二次跳3 m，小猴这时候距离原来地方是5 m.

C. 小猴朝东第一次跳2 m，再朝西第二次跳3 m，小猴这时候距离原来地方是1 m.

D. 小猴朝西第一次跳2 m，再朝东第二次跳3 m，小猴这时候距离原来地方是1 m.

这时候，我们画出数轴来表示.

可以在数轴中观察出，小猴所处的位置在A、B、C、D.所以一些看上去条理很复杂的题目，通过数形结合画出数轴就很直观地发现答案，这样解题更加的方便快捷，并且准确率极高[3].

与此类似的方法在另外一道练习中也出现了：

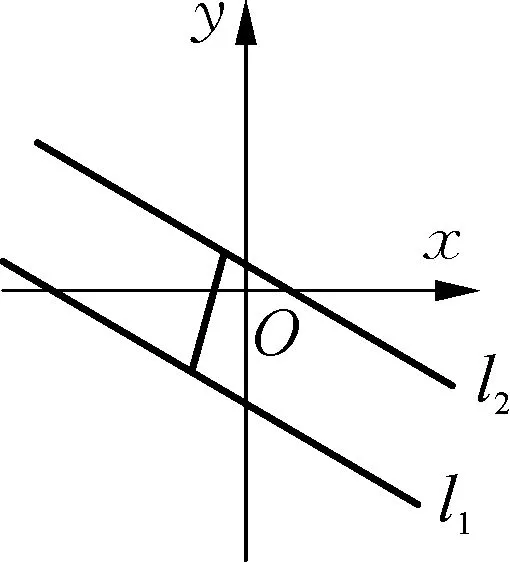
题4假设a、b两个数在数轴上如图所示，a+b0，a+(-b)0，(-a)+b0，(-a)+(-b)0.

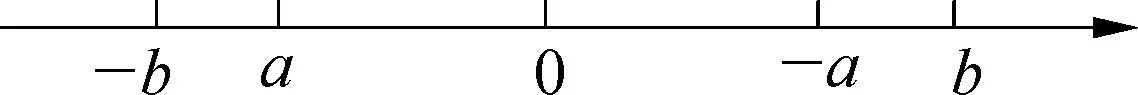
像这样的题目，我们可以用数形结合的思路作为解题的切入点，根据数轴，我们可以观察出，a+b>0，a+(-b)<0，(-a)+b>0，(-a)+(-b)<0.

任何一个有理数可以用数轴上面的一个点来表示，在运用数形结合的思路，观察数轴上的点的位置之间有什么关系，就可以很清楚地呈现出来.数轴可以让不清晰的题目清晰地表达出来，让难解的问题变得清楚明白.

3 数形结合在解决三角形面积中的运用

在随堂练习中，一些学生看到三角形就感觉这个图形认识他，可是他对这个图形就是找不到解题的思路.那我们可以用以下两种方法来轻松解决三角形面积的问题.第一种方法是：我们可以先画一个直角坐标系，再在直角坐标系中，画出该三角形，我们用割补法进行解题；第二种方法是：我们画一个正方形或者长方形，再在中间画出该三角形.可是这种方法只能用在能用勾股定理求解的三角形面积的问题中[4].

题5如图，P是正方形ABCD内一点，如果P到CD是10，PA=PB=10,那么求△APB的面积.

解：∵过点P作EF⊥AB于E，交于CD于F，

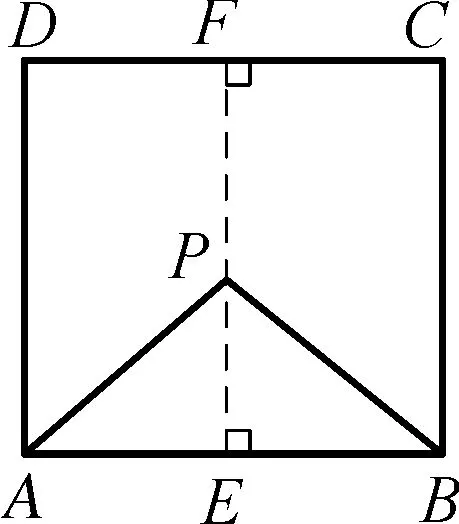
∴PF⊥CD，PF=PA=PB=10,E是AB的中点.

设PE=x，那么AB=FE=10x，

∵E是AB的中点，

∴AE=1/2AB=1/2(10x).

∵Rt△PAE中，PA2=PE2AE2，

∴102=x2[1/2(10x)]2，

∴x=6，

∴PE=6,AB=16，

∴△APB的面积是16×6÷2=48.

我们在思考这道题目的时候，可以先在点P画出垂线，过点P作EF⊥AB于E，交于CD于F得到了Rt△PAE.这时候我们要求△APB的面积，就只要算出AB和PE的长就可以了.那我们观察图形，先设PE=x，那么AB=FE=10x，这样我们就轻而易举算出了AE，Rt△PAE中，PA2=PE2·AE2，将数字代入这个方程，就可以算出AB和PE的长，知道了三角形的两边，求面积就特别简单.

4 数形结合在方程应用题中的运用

中学的方程应用题是一个难点，面临着杂乱的题干，学生就是找不出数量关系.我们可以将数量关系用图的形式表现.比如：线段、表格等.这样让学生更好地梳理题干中的杂乱成分，使之借助图形体现出直观性.

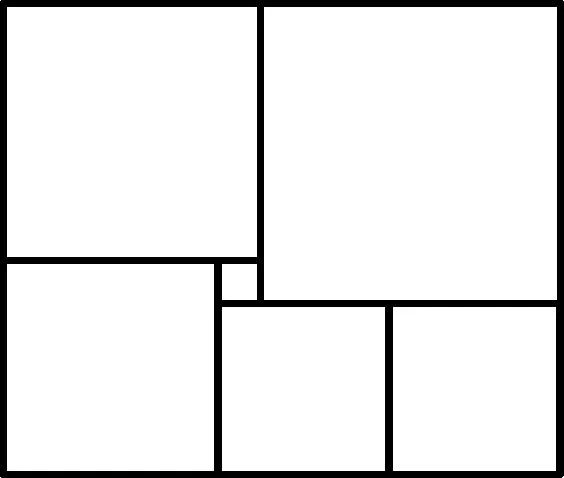
题6根据图片显示，在电脑屏幕上出现的矩形图，是6个正方形组合而成的，中间最小的一个正方形的边长是1，那么这一整块的正方形的面积是多少？

解：设右边两个相等的正方形的边长为x.那么，我们按顺时针的方向就可以知道其他三个正方形的边长分别是：x+1,x+2,x+3.我们知道矩形的对边是相等的，所以得出x+x+(x+1)=(x+2)+(x+3)，算出得数x=4.因此(x+2)+(x+3)=13，(x+2)+(x+1)=11.

所以13×11=143.答：矩形的面积为143.

像这样的题目，我们应该先观察图，题干中除了边长为1的正方形，还有5个正方形，其中有2个的大小是一样的，那么我们根据数形结合就可以得知顺时针方向上的正方形的边长依次大1.

5 数形结合在集合问题中的运用

在历年的数学练习试题中，或多或少的出现关于集合的题目.那我们在解题的思路中，就要想到利用数轴或者韦恩图来思考.图示法也可以解决集合问题.对于一些不知道从哪里入手的集合问题来说，我们可以用韦恩图、数轴、图表等来加以辅助，这样找到解题思路，就可以把无从下手的题目拨开云雾，让解题更加简便.

题7已知集合M={x|x2-3x-28≤0}，N={x|x2-x-6<0}则M∩N为

( )

A. {x|-4≤x<-2或3

B. {x|-4≤x<-2或3≤x<7}

C. {x|x<-2或x>3}

D. {x|x<-2或x≥3}

这道关于集合的试题，我们在构思中可以想到用一元二次不等式的解集来进行运算，再把数轴画出来，用形来辅助数，这样我们可以得出这道题目的选项是A.

6 数形结合在几何证明中的运用

我们在几何的题目中，要把数字和数轴上的点相对应、函数和图形相对应，在条件中的等式、代数式都明确有几何的意义.题目中给出的条件里面有几何图形的时候，都相应有代数的体现，他们之间可以相互转换[5].

题8如图，OC是∠AOB的平分线，在OC上的P点，PE⊥OB，PD⊥OA，点E和点D分别垂足.求证：PE=PD.

解：∵PE⊥OB，PD⊥OA，点E和点D分别垂足，

∴∠PEO=∠PDO=90°.

∵OC是∠AOB的平分线，

∴∠1=∠2，又OP=OP.

∴△PDO≌△PEO.

∴PE=PD.

这道题目的关键在于角平分线上的点，到这个角的两边距离相等.通过数形结合的方法，我们很快可以得知，这两个三角形全等，那么这两个三角形相对应的边肯定也是相等的.这样我们把抽象的几何图形具体化地呈现出来，利用图形找出他们之间的关系.

7 数形结合在线性规划问题中的运用

相信许多学生对于线性规划这个词比较陌生，那我们先来理解下什么叫做线性规划.首先，我们把要解的最大值、最小值的函数的变量满足的不等式组叫约束条件.其次，要是变量的一次函数，就称为线性目标函数.要是约束条件是不等式的话，那就叫线性约束条件.在线性约束条件中，求最大值、最小值，叫线性规划问题.最后，要是满足线性约束条件下的解(x，y)叫可行解.在解线性规划题目的时候，我们一般先列出未知数、约束条件、目标函数，再画出可行域，然后将目标函数变成直线方程，平移直线，直线的交点就是我们所要的答案.

( )

A. 10 B. 12

C. 14 D. 15

许多学生面对这种题目，没有一点头绪，无从下手.有的甚至连题目都看不懂.面对这样的题目，我们先要保证看清题干，把线性约束条件的可行域给画出来，最后确定最优解，就可以得出目标函数z=3x+y的最大值.

解：如图，我们先把线性约束条件的可行域给画出来，观察图形可以得出最优解是(3,1)，所以这道题目的答案是10，所以选A.

8 数形结合在函数问题中的运用

在数学题中，我们要是遇到函数问题，我们可以用图形来作为切入点，图形中的几何的特点和函数有着密切的关系.

8.1 数形结合解决函数的定义域

在练习中，学生看到函数的定义域问题，头脑就开始不清晰.这时候，我们要做的是把函数中有意义的条件给找出来，再用适合的图形把它表现出来.

题10已知函数f(x)的定义域是[a,b]其中a<0b,求函数g(x)=f(x)+f(-x)的定义域.

这道关于函数的试题，我们的思路是：如果g(x)的定义域为M,f(x)和f(-x)的定义域分别为A、B，那么M-AnB，我们可以在数轴中知道要求的是哪里.

解：∵函数f(x)的定义域为[a,b]，

∴a≤x≤b.

∵要让f(x)有意义，

∴a≤-x≤b，

∴-b≤x≤-a.

∵a<0

∴-b<0<-a.

∵|a|>b>0，

∴a<-b.

∵函数g(x)的定义域{x|a|≤x≤b}n{x|-b≤x≤-a}={x|-b≤x≤b}.

如果这种题目在考试中以选择题的形式出现，那就更简单了.都不用去一步一步计算，运用图形就可以做出来了.

8.2 数形结合解决函数的值域

有些数学考试的题型中，题目本身给出了定义域，让考生去求值域的题目.考生要是直接算，就不知道该从哪里算起.那我们换个思路，要是把这些数用图形表现出来，那么在图中，就能很清楚的展现出来.

题11求函数y=|x-2|-|x-4|的值域.

这样的题目，我们就从变量x的范围讨论去掉绝对值，将函数表示为分段函数，画出分段西数的图象，从图象中我们就可以看出y的范围是多少.

可以根据图形得知y∈[-6,6].

在实际的题型中，要灵活运用数形结合的方法，会使问题明朗，不再看过去一头雾水.

9 数形结合在复数中的运用

复数在中学数学中是重点学习内容之一，它包含三角、代数、几何等.复数和几何有着不可分割的意义.我们通过数形结合的运用，可以有效地解答出有关复数的问题.

题12已知复数z=(m2-2m-3)+(m2-4m+3)i(m∈R)在复平面上的对应点为Z，求实数m取什么的时候，点Z在实数轴上？数m取什么的时候，点Z在虚数轴上？数m取什么的时候，点Z在第一象限？

解：要想点Z在实轴上，那么复数的Z为实数，因为m2-4m+3=0，通过计算可以得知，m=3或者m=1，所以m=3或者m=1的时候，点Z在实轴上.

要想点Z在实虚轴上，那么复数的Z为虚数或者是0，因为m2-2m-3=0，通过计算可以得知，m=3或者m=-1，所以m=3或者m=-1的时候，点Z在虚轴上.

要想点Z在第一象限上，那么复数的Z为实部、虚部都必须大于0，因为m2-2m-3>0，m2-4m+3>0，通过计算可以得知，m<-1或者m>3.所以m<-1或者m>3的时候，点Z在第一象限上.

这样的题目，我们首先要考虑的是点Z的位置确定复数Z实部和虚部的取值情况.

10 数形结合在最值问题中的运用

最值问题一直是中学数学长期以来最爱考的一个知识点，数形结合恰好是解题的妙招.

题13已知a、b、c、d∈R，a+2b+4=0，c+2d-1=0,求S=(a+b)2+(b+d)2的最小值.

11 结语

总之，代数以图形来思考，图形以代数来切入，这就是数和形的转化，方便考生们来应对练习的难题.数通过形来表示，就会变得直观；形有了数后，变得更加的具体.