谐波干扰下共享电源计量装置运行误差预补偿方法
马昊燕,李叶飞,张 涛,郭炜炜
(国网宁夏电力有限公司,银川 750001)
0 引言
共享电源计量装置是电力系统的重要组成部分[1],能够有效地计量电能应用情况,为电力系统计费与收费提供有力依据[2]。但共享电源计量装置实际应用过程中易受到谐波影响[3],由此降低装置计量结果的准确性,研究一种有效的谐波干扰下共享电源计量装置运行误差预补偿方法具有重要意义。
于海波与王春雨等人将PCA-SVR技术引入电能计量装置误差分析中,有效评估电能计量装置误差,并基于评估结果进行误差补偿[4]。王生东与李浩然等人利用过零检测技术等实现电能计量装置的相位误差补偿[5]。张鼎衢与林国营等人采用模糊层次分析理论分析电能计量装置运行状态,确定其误差,并基于分析结果采用相应方式进行误差补偿[6]。但上述研究方法在实际应用过程中均未考虑谐波干扰问题,因此实际补偿结果具有一定偏差。基于此,提出谐波干扰下共享电源计量装置运行误差预补偿方法,提升共享电源计量装置应用性能。
1 共享电源计量装置运行误差预补偿方法
1.1 谐波干扰下共享电源计量装置运行误差分析
共享电源计量装置由数字乘法器与电压/频率转换器等器件共同组成,图1所示为共享电源计量装置结构。
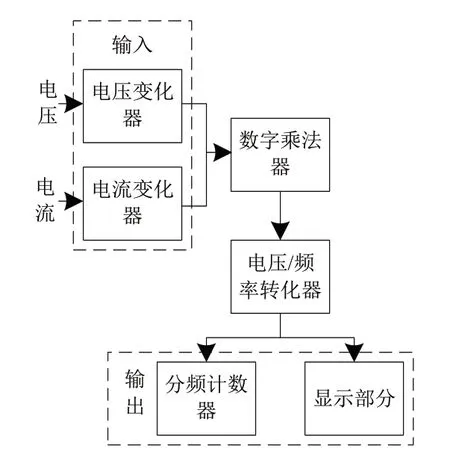
图1 共享电源计量装置结构图
共享电源计量装置根据相应比例,利用电压变化器与电流变化器修正电压与电流信号,令其与数字乘法器可用信号格式一致[7];通过数字乘法器得到固定时间区域内的功率均值,并将所获取的功率信号均值转换为频率脉冲信号。基于所获取的频率脉冲信号,通过频率信号技术方式获取此时间区域内的电量。
以时分割乘法器为数字化乘法器,受谐波干扰,乘法器的电压信号被划分为两部分[8],分别是u1、u2,如式(1)所示:

式(1)内,φo和t分别表示基波角频率和时间。
以ig和ug分别表示乘法器电流和电压,规范化采样下采集频率过程中,受g次谐波干扰,可通过式(2)计算ig和ug:

式(2)内,Ig和Ug分别表示g次谐波干扰下电流与电压的有效值,φg和δg分别表示谐波角频率和g次谐波干扰下电流与电压的相位差。
以Z表示调制频率,通过式(3)描述单采样周期中基波划分数量:

式(3)内,z1表示工频。

受g次谐波干扰后,以igk表示划分ig的第k份,其公式描述为:

受g次谐波干扰后,以ugk表示划分ug的第k份,其公式描述为:

受g次谐波干扰后,规范化采样频率条件下功率值计算过程为:

通过式(8)能够计算Pg同实际信号频率f条件下的功率Pgf间的差值:

受g次谐波干扰后,通过式(9)计算共享电源计量装置的功率计量误差:

式(9)内,Kg表示产生g次谐波电压的初相角。
利用式(10)计算基波叠加若干次谐波条件下的计量误差:

式(10)内,下标0和d分别表示谐波次数上限。
基于上述过程能够实现谐波干扰下共享电源计量装置运行误差分析。
2.2 基于RBF神经网络的运行误差预补偿
采用RBF神经网络实现谐波干扰下共享电源计量装置运行误差预补偿。
补偿前需调节共享电源计量装置运行误差内的比例、积分与微分系数,令三个系数间能够彼此牵制且彼此配合[9]。考虑三个系数间不具备一次函数相关性[10],所以三个系数间不具备线性相关性,因此基于三个系数间的非线性相关性能够得到基于RBF神经网络的共享电源计量装置运行误差预补偿过程中的最优权值。
以e(k)表示谐波干扰下共享电源计量装置运行误差第k次采样的输出结果为:
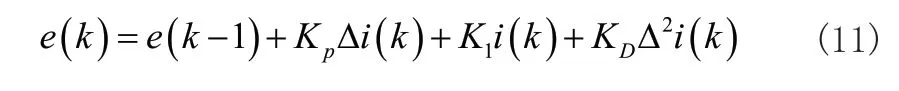
式(11)内,Kp、K1和KD分别表示比例、积分与微分系数,i(k)表示第k次采样输入共享电源计量装置运行误差值电流。式(11)内,将三个系数定义为同共享电源计量装置运行状态高度相关的可调系数[11],由此可将式(11)转换成为:

式(12)内,f表示激发函数。
设定m和xj,j=1,2,...,m分别表示RBF神经网络的输入层节点数量和输出层输出结果,其中m值受共享电源计量装置复杂度影响。
为降低RBF神经网络对于谐波干扰下共享电源计量装置运行误差训练复杂度,在训练样本即谐波干扰下共享电源计量装置运行误差样本完全能够描述误差基本特征的条件下[12],经由科学的学习机制完善训练样本质量,由此获取RBF神经网络的最优训练样本。
以ni(k)和ri(k)分别表示RBF神经网络隐含层输入和输出,其公式描述为:

式(13)内,vij和q分别表示隐含层加权系数与节点数量。
通过式(14)得到谐波干扰下共享电源计量装置性能指标函数:

式(14)内,b(k)和y(k)均表示采样值。依照谐波干扰下共享电源计量装置性能指标负梯度方向确定加权系数[13],同时为提升收敛速度引入惯性项∂:

式(15)内,ρ和ε分别表示学习率与惯性系数。持续优化学习速率补偿所导致的偏差,由此得到:

通过性能函数优化后能够获取RBF神经网络输出层同隐含层的最优权值,如式(17)所示:

基于上述过程,在获取谐波干扰下共享电源计量装置运行误差预补偿的最优权值过程中,需设定不同层加权系数的初始值wli(k)和vli(k),同时通过ρ和ε计算权值。获取谐波干扰下共享电源计量装置运行误差采样值后,计算神经元结构输出,为获取谐波干扰下共享电源计量装置运行误差预补偿奠定基础。
基于上述过程所得的RBF神经网络最优取值,采用协同量子差分进化算法优化RBF神经网络参数,通过量子遗传算法优化RBF神经网络结构与隐含层节点数量。因此实际获取谐波干扰下共享电源计量装置运行误差预补偿过程中,RBF神经网络优化可划分为三个种群:参数种群、结构种群和隐含层种群。以合作型协同搜索策略作为三个种群的优化机制,由此将具有高度复杂性的问题划分成不同的简单问题,各简单问题通过有所差异的种群并行搜索,确定适应度值过程中各种群需交换最优信息[14]。
协同量子差分进化算法计算流程如图2所示。

图2 协同量子差分进化算法计算流程
协同进化机制所描述的是合作型进化模式,将其应用于基于RBF神经网络的谐波干扰下共享电源计量装置运行误差预补偿问题中,是将该问题的完整解划分为若干个部分,不同部分间基于合作方式交换信息。量子遗传算法优化RBF神经网络结构种群与隐含层种群,差分进化算法优化参数种群,不同种群间适应度函数评价过程的同时完成信息交换[15]。
将协同量子差分进化算法应用于谐波干扰下共享电源计量装置运行误差预补偿问题中,优化RBF神经网络的具体过程如下:
第一步:初始化种群。设定协同量子差分进化算法的种群规模、迭代次数上限、隐含层种群以及参数种群;同时设定量子遗传算法与差分进化算法中的相关参数。
第二步:基于种群个体匹配确定适应度值获取参数种群的最优个体xb。
第三步:基于xb与结构种群内随机合体实施配对,确定适应度值,获取隐含层最优个体hb。
第四步:基于xb和hb,分别同结构种群内不同个体进行配对,确定适应度值,由此获取参数结构种群最优个体Pb。
第五步:通过更新优化过程优化不同种群的最优个体。
第六步:确定是否符合结束标准,若符合,则输出最优RBF神经网络;若不符合,即返回第四步。
利用协同量子差分进化算法优化RBF神经网络结构,通过优化后的RBF神经网络持续优化权值,实现谐波干扰下共享电源计量装置运行误差预补偿。
3 实验结果
为验证本文所研究的谐波干扰下共享电源计量装置运行误差预补偿方法的实际应用性能,选取某市电力系统中所使用的共享电源计量装置为研究对象,利用MATLAB软件构建研究对象的三相电源计量装置,通过本文方法确定谐波干扰次数有所差异的条件下,研究对象的运行误差预补偿性能,所得结果如下。
3.1 研究对象功率采样误差分析
通过本文方法确定谐波干扰次数有所差异的条件下,研究对象功率采样误差,所得结果如图3所示。


图3 功率采样误差分析结果
三相运行误差整体变化趋势具有较高一致性,均表现出运行误差随谐波次数提升而提升的趋势。其中,A相与B相的运行误差波动范围为-3×10-4%~3×10-4%,而C相的运行误差与其他两相相比较小,波动范围在-1×10-4%~1×10-4%内。本文方法能够有效实现谐波干扰下研究对象运行误差的计算。
3.2 预补偿性能分析
采用本文方法对研究对象运行误差进行预补偿。在谐波干扰次数为12次的条件下,本文方法补偿前后研究对象运行情况如图4所示。由于研究对象C相运行误差较小,基本可忽略;其他两相运行误差波动态势具有较高一致度,所以在分析本文方法运行误差预补偿性能过程中仅以A相为例。

图4 A相功率采样误差预补偿前后对比结果
采用本文方法对研究对象运行误差进行预补偿前,研究对象A相功率曲线具有显著的间断性,同时曲线具有一定的粗糙性。采用本文方法对研究对象运行误差进行预补偿后,研究对象A相功率曲线具有较好的连续性与平滑性。实验结果表明本文方法能够有效实现研究对象运行误差的预补偿,提升研究对象功率计量准确性。
以A相为例,设定谐波干扰次数为12次,进一步验证本文方法对研究对象运行误差的预补偿效果。分析本文方法在有所差异的实际采样频率条件下,运行补偿补偿前后的波动情况,所得结果如表1所示。

表1 运行误差预补偿前后研究对象功率变化情况
4 结语
本文提出谐波干扰下共享电源计量装置运行误差预补偿方法,基于谐波干扰下共享电源计量装置运行误差分析结果,采用RBF神经网络实现运行误差预补偿。实验结果本文所采用方法能够有效计算共享电源计量装置的运行补偿,大幅降低共享电源计量装置的功率误差。本文方法能够有效确定实际采样频率,同时所确定实际采样频率同规范化采样频率间的差异较小,基本控制在0.03Hz之内;在采样频率逐渐降低的条件下,功率计算结果同功率规范化结果间的误差呈逐渐提升趋势。采用本文方法补偿前,功率值误差上限达到0.1%;采用本文方法补偿后,研究对象功率值误差上限仅为0.03%。由此说明采用本文方法对研究对象运行误差进行预补偿后,能够显著降低实际输出功率与功率规范化值间的差异性。但是,本研究还不存在一定的弊端,主要是现场干扰源多样,无法准确界定干扰类型,这是下一步需要进一步解决的问题。

