基于粒子群优化分数阶PID的阀门开度控制

朱 敏，臧昭宇，赵聪聪

（合肥工业大学 电气与自动化工程学院，合肥 230009）

0 引言

调节阀在工业控制系统中应用广泛，在化工、冶炼、核电和污水处理等领域发挥着重要作用[1]。然而调节阀工作环境恶劣，具有非线性、滞后性和时变性等特征，导致阀位控制易超调，到达稳态时间长。在阀门开度控制策略方面，国内外学者做了很多工作。文献[2～3]提出新的滑模控制器，减少抖振并保证了闭环系统的稳定性。文献[4～5]针对阀门定位器精度较差的劣势引入模糊控制，提高了系统控制精度和响应速度。文献[6]提出基于模型的自适应状态观测器，所提出的观测器有效且易实现。文献[7]将仿人智能控制应用到阀门开度控制系统中，使系统具有较好的动态性能和鲁棒性。文献[8]提出BP神经网络整定PI控制器，所提出方法具有良好控制效果。其中有些策略还在研究阶段，至今实际工程应用中仍以PID控制器或PI控制器为主，难以实现对阀位精确有效的控制，通常出现到达稳态时间长，稳态误差较大的缺点[9,10]。

目前少有学者将分数阶控制理论应用到阀门开度控制系统中，分数阶PID在原有的PID控制器基础上增加了微分阶次λ和积分阶次μ，尽可能地提高系统的鲁棒性和稳定性，可以灵活的调节被控系统，使之达到要求的性能指标。因此，针对阀门开度控制系统，本文将分数阶微积分和PID控制器相结合，采用最新提出的改进粒子群优化算法对控制器参数整定，设计阀门开度PIλDμ-气室气压P的串级控制方法，通过整定6个参数（Kp1，Ki，Kd，λ，μ，Kp2）以获取合理的控制器参数值。仿真结果表明，所提出的控制方案提高了阀位控制系统的稳定性和快速性，为控制阀门开度提供了一种可靠的方法。

1 阀门控制系统工作原理和建模

调节阀的串级控制系统设计方案如图1所示，它由分数阶PID控制器、比例P控制器、电气比例阀、单/双作用气缸、调节阀、压力传感器和位移传感器等部件组成。分数阶PID将接收的反馈阀位信号和上位机输入的控制指令运算处理后，输出脉宽调制信号驱动电气比例阀，比例控制P将分数阶PID输出的信号和接收的反馈压力传感器信号进行运算处理，并输出气压信号，进而改变气缸中的气压，带动调节阀中阀杆运动，从而改变阀门开度[11]。

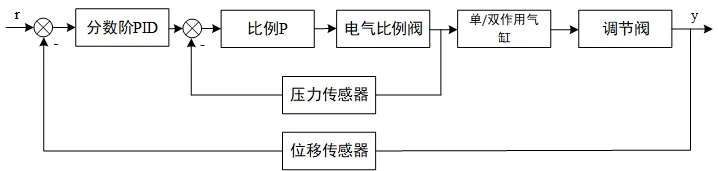
图1 调节阀串级控制系统

阀门控制的终端部分主要由电气比例阀、单/双作用气缸、调节阀体组成。气缸和调节阀共同组成气动执行机构。以双作用气缸为例，其控制的终端机构图如图2所示。

图2 阀门控制的终端机构

电气比例阀作为气压放大装置，将电信号转换成气压驱动气动执行机构完成阀门动作。假设外部环境和气源压力恒定，气动介质为理想气体，对比例阀阀芯受力分析，有如下微分方程：

式(1)中，A1和A2分别为阀芯顶部和底部的截面积，k为弹簧系数，x1为弹簧压缩量，p1和p2分别为先导腔压力和比例阀输出压力，Ff为摩擦力。由质量守恒定律知进入比例阀内气体质量流量与气缸内质量变化率相等，有：

G为气缸气体质量流量。ρ为气体密度，V为气缸体积。假设气体进入气缸过程瞬间完成，由热力学第一定律：

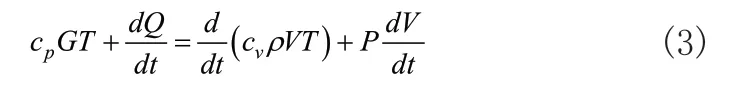
cpGT为介质内能，T为理想气体温度，cp和cv分别表示比压系数和比容系数,dQ/dt为单位时间气缸与外界交换的热量；PdV/dt为单位时间气缸气体变化所做功。若气体进入气缸立即充满全腔且过程绝热，则dQ/dt=0，pdV/dt=0。气体压强与气体密度之间的表达式为：

R为理想气体常数，根据气体比热r=cp/cv和R=cp-cv，由式(3)和式(4)得：

式(5)拉氏变换后为比例环节，验证了比例阀放大作用。综合由式(1)和式(5)，为方便分析，可将比例阀可看作一个含有比例特性的二阶震荡环节。

薄膜气缸可看作气动阻容环节，微分方程为：

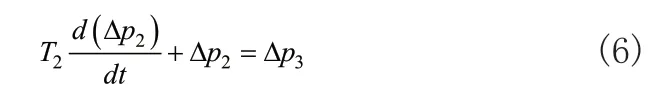
p2为比例阀输出压强，p2为比例阀输入压强，T2为气动阻容时间常数，气动执行器可看作含有纯滞后的惯性环节：

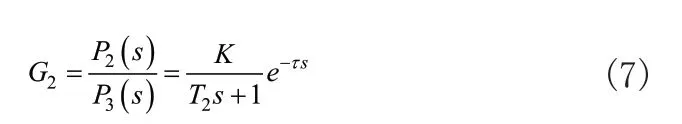
其中T2=R·C,R=α·l/α，R为气路气阻，α为气路截面积，α为气阻系数，l为气路长度，K为放大系数。

对阀杆分析，当气缸中气体作用在阀杆顶部膜片上的压力大于阀杆受到的摩擦力和弹簧弹力之和时，阀杆会运动。由牛顿第二定律得阀杆力平衡方程：

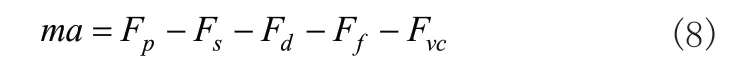
其中Fp为气室压力，Fs为弹簧反作用力，Fd为弹簧预紧力，Ff为静摩擦力，Fvc为介质反作用力。忽略Fvc,对式(8)展开得如下微分方程：

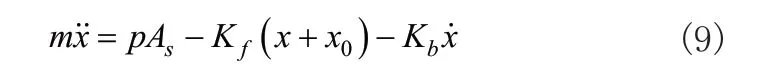
式(9)中m为阀杆部件质量，p为气缸相对气压，As为气缸薄膜面积，Kf为气缸中弹簧刚度系数，x和x0分别为弹簧压缩量和弹簧预压缩量，Kb为阀杆动摩擦系数。忽略x0，因此阀杆运动数学模型的传递函数近似表示为：

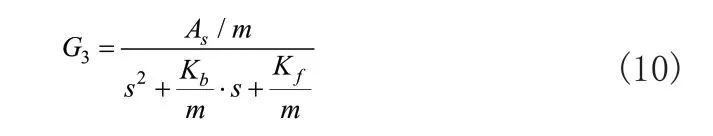
2 分数阶PID参数设计

分数阶PID是在分数阶微积分理论的基础上对整数阶PID的发展，其传递函数表达式为：

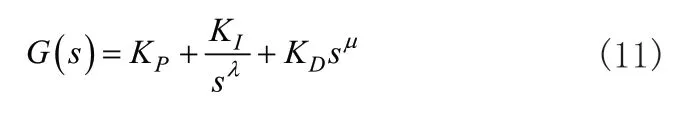
图3为分数阶PID控制器平面。由于多了两个参数，使分数阶PID的可调参数更广，控制器可以更灵活的控制被控对象，从而满足复杂系统性能指标。

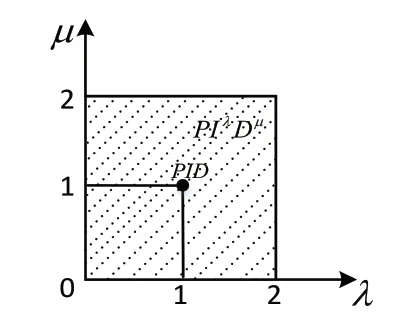
图3 分数阶PID控制平面图

图4为分数阶PID控制系统模型。r(t)、u(t)和y(t)分别为系统输入、控制器输出和系统输出。G(s)为被控对象。

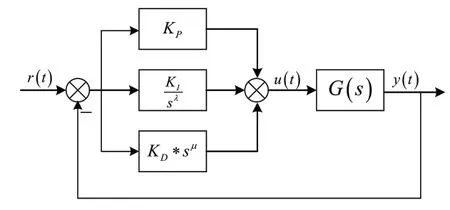
图4 分数阶PID控制系统模型

本文通过Oustaloup滤波法[12]，设近似频段的范围为[wb,wh]，将微积分分数阶算子近似成整数阶形式，传递函数为：

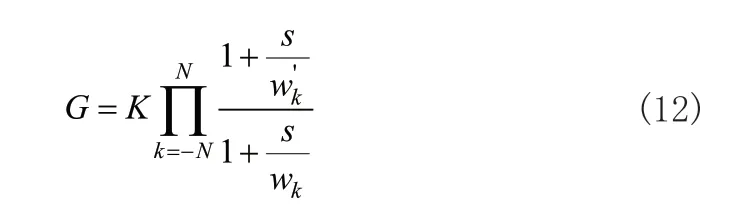
式(12)中，K为增益，N为阶次，w′k和wk分别表示零点和极点，其中：

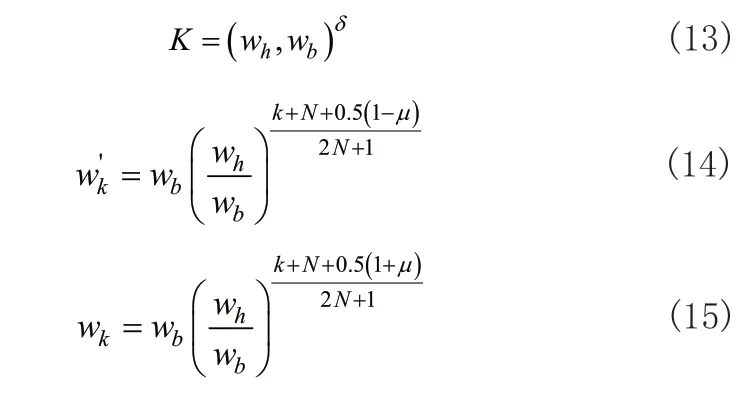
式(13)中δ为分数阶阶次。这样通过滤波器就能使分数阶PID得以实现。

3 标准粒子群算法及改进

3.1 标准粒子群算法

粒子群优化算法[13]，又称微粒群优化算法（Particle Swarm Optimization），源于对鸟群觅食等过程中的行为模拟。假设粒子种群的规模为S，粒子种群的搜索空间为D维，记X为第t次迭代所有粒子的位置，那么第i个粒子的位置为,设粒子i经历的最优位置即个体极值为,整个粒子群的最优位置即全局极值,设第i个粒子的第t次迭代速度为，则粒子i在t+1次迭代更新速度和位置的计算如式(16)所示：

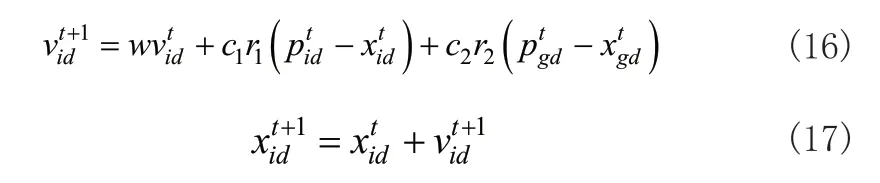
式(16)中d=1,2,…,D,s=1,2,…,S。D为惯性权重系数，c1和c2为学习因子，r1和r2为(0,1)区间的随机数。

3.2 改进PSO算法

在PSO算法中粒子通过迭代产生新的位置，新的位置由前代的迭代位置和当代的速度决定。粒子速度更新由三部分组成：粒子先前的速度，粒子的“自身认知”部分和粒子的“群体认知”部分。惯性权重ω决定上一代的种群速度对新一代的种群速度影响程度，当惯性权重ω的取值较大时，粒子具有较强的全局探索能力，但收敛速度较慢；当惯性权重ω的取值较小时，粒子具有较强的局部搜索能力，但容易陷入局部最优。

典型的惯性权重ω取值采用线性递减策略：

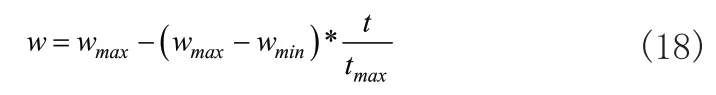
式(18)中t为当前迭代次数，tmax为最大迭代次数。基于线性惯性权重递减方法使得粒子在迭代前期和后期具有不同的惯性权重，一定程度上提高了寻优能力，但在整个迭代过程中惯性权重的变化率是固定值，在局部搜索和全局搜索上强度一致，可能在全局搜索时找不到全局最优或在迭代后期无法在全局最优值更好的逼近。

文献[14]使用改进粒子群优化分数阶PID，对权重系数最小值和最大值设置上下限，并使其随迭代次数按照指数函数非线性降低。具体为：

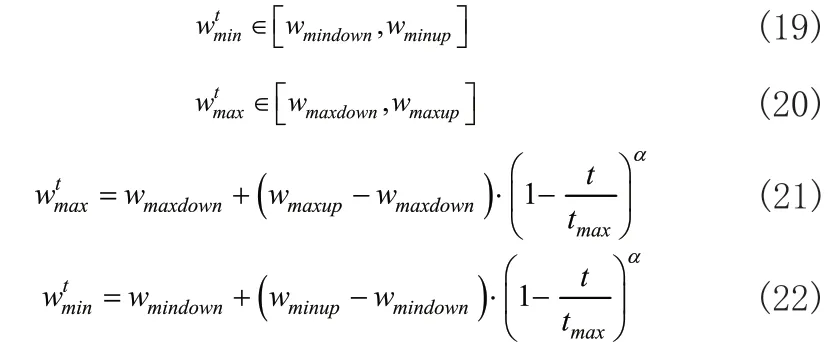
式(21)和式(22)中α为幂系数，一般为正整数。wtmin和wtmax分别为第t次迭代惯性权重最小值和最大值。由图5看出，惯性权重在迭代初期下降的很快，在迭代后期变化率减小，下降的慢。尽管该方法改变了惯性权重变化率，但存在缺点：粒子在迭代初期时具有较大的权重系数，随着迭代次数增加，惯性权重快速下降，易使得在前期较少迭代的次数内全局搜索不足导致找不到全局最优解，或粒子群已找到全局最优解但迭代后期惯性权重过小，粒子局部搜索能力较强而陷入局部最优解，得不到最优的结果。

因此本文提出新的方法对文献[14]法进行改进，引入正弦变化将惯性权重公式改为：

取wtmin∈[0.3,0.6]，wtmax∈[0.7,1.2]，tmax=100，以幂系数α=3为例，文献[14]和本文改进法权重系数随迭代次数增加的变化趋势如图5所示。

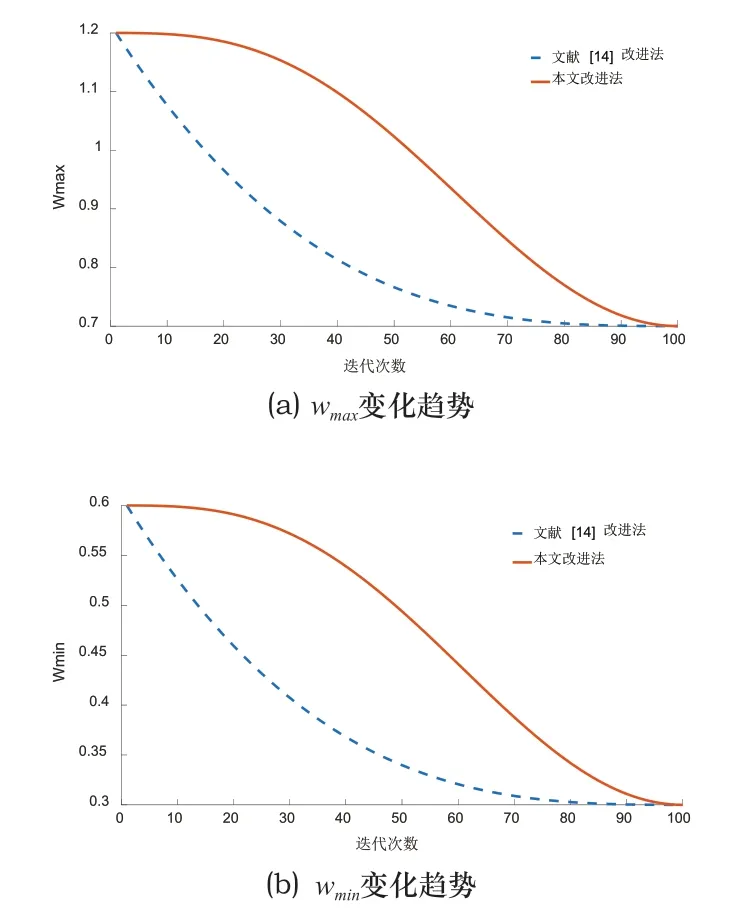
图5 权重系数变化趋势对比

可以看出在迭代前期ω变化率小，下降较慢，粒子群在前期有较长时间的全局搜索，有利于找到全局最优解，搜索中期ω变化率大，下降迅速，在搜索后期粒子群具有较强的向全局最优靠近能力，提高算法的优化精度。

另外，在迭代过程中，不同粒子具有不同的适应度值，高适应度值的粒子离较优位置远，适合使用较大权重系数以增强粒子全局搜索能力，低适应度值的粒子离较优位置近，适合使用较小惯性权重系数以提高粒子搜索精度。在每次迭代后，将所有粒子按适应度值从高到低排序，排序后粒子i的适应度值序号设为δi(i=1,2,...,S),则第t次迭代时粒子i的权重系数为：

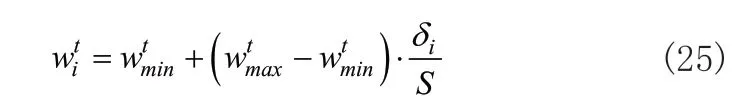
PSO算法中学习因子c1和c2分别调节个体认知部分和社会认知部分在粒子飞行速度中所占比重，A.Ratnawecra等人提出了异步线性改变学习因子法[15]，即随着迭代次数增大，学习因子c1减小，学习因子c2增加。在A.Ratnawecra等人的基础上，本文对学习因子公式加入粒子适应度值项，当迭代次数增加时，适应度小的粒子使用较大c1利于搜索全局空间遍历，不会很快聚集到局部最优；适应度大的粒子使用较小c2利于粒子向全局最优靠近。如式(26)所示：

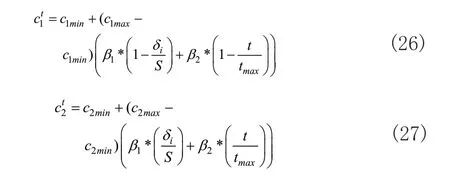
c1min、c2min为学习因子c1的最小值，取值均为0.2；c1、c2为学习因子c2最大值，取值均为2.2；β1和β2为权值系数，分别取0.3和0.7。改进后的公式综合了迭代次数和粒子的适应度值对学习因子进行选取，将迭代次数和适应度值序号赋予不同权重求取学习因子，提高获得满意最优解的可能性。

3.3 改进PSO对分数阶PID的参数整定

本文根据阀门控制系统的阀门开度输出信号设计性能指标，将外回路分数阶PID参数和内回路比例参数（Kp1，Ki，Kd，λ，μ，Kp2）作为单个粒子6个分量，对这些参数进行寻优计算。

根据适应度函数的值衡量粒子群对参数寻优结果的好坏，选取ITAE性能指标(系统的绝对值误差和时间的积分)，可以反映系统的精确性和快速性，同时可兼顾较小超调量以尽量避免阀门开度控制产生超调；为防止外环控制量输出过大在目标函数中加入外环控制器输出平方项。目标函数为：

式(28)中，e(t)为控制误差，u(t)为外环控制器输出量，λ1和λ2为权重系数，λ1和λ2分别取0.999和0.001。

改进PSO优化分数阶PID参数步骤如下：

步骤1：粒子种群初始化，包括种群的规模、最大迭代次数，搜索区域的范围、粒子的初始速度和初始位置、惯性权重的最大值和最小值的范围以及学习因子c1、c2的最小值和最大值.

步骤2：根据式(28)计算每个粒子适应度值.

步骤3：比较当前粒子的适应度值与个体最优适应度值，取较优值作为个体最优适应度值并保存该位置。

步骤4：比较当前粒子适应度值和全局最优适应度值，取较优作为全局最优适应度值并保存该位置。

步骤5：将种群中所有粒子适应度值由高到低排序，并根据迭代次数确定权重系数最大值和最小值，然后计算粒子的惯性权重系数。

步骤6：由式(26)和式(27)确定学习因子c1、c2。

步骤7：更新粒子的速度和位置。

步骤8：判断迭代是否结束，如果结束则退出，否则返回步骤2继续迭代。

4 实验仿真

为检验改进粒子群优化分数阶PID参数的效果，采用阀门开度PIλDμ-气室气压P的串级控制思路，建立双闭环阀门开度控制系统模型，内环使用比例系数P控制电气比例阀输出气室气压信号，提高系统快速性和抗干扰性，外环采用PIλDμ控制器以获得精确的阀门开度。

利用Simulink搭建阀门开度控制系统模型。设置粒子群规模S为50，最大迭代次数tmax=100，最小适应度值为0.1，权重系数最小值范围取wtmin∈[0.3,0.6]，最大值范围取wt

max∈[0.7,1.2]；学习因子最小值c1min、c2min均取0.2，学习因子最大值c1max、c2max均取2.2。幂系数α取3。外环分数阶PID参数取值范围为：Kp1∈[0.01,20]，Ki∈[0.01,10]，Kd∈[0.01,10]，λ∈[0.1,2]，μ∈[0.1,2]，内环比例参数Kp2∈[0.01,20]。给定系统输入为单位阶跃信号。将标准PSO算法、文献[14]改进的PSO算法、本文改进的PSO算法三者各进行10次实验，取平均值作为参数对比，得到平均适应度值曲线如图6所示。

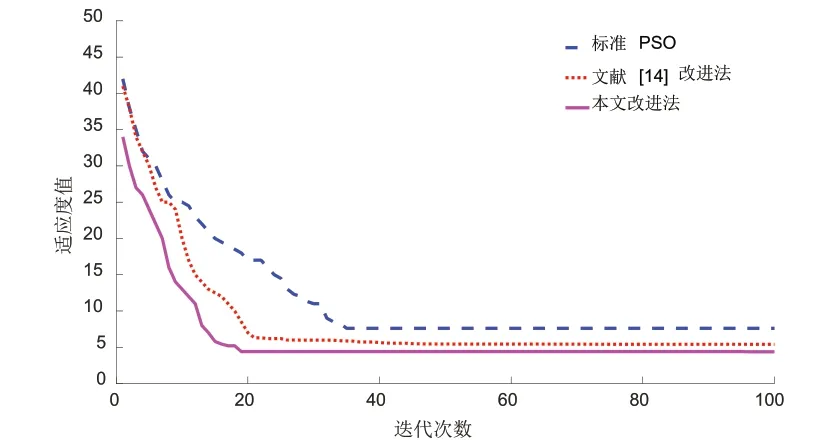
图6 最优个体平均适应度变化

如图6所示，标准PSO算法和文献[14]改进法分别在36代和22代基本趋于稳定，本文改进法在18代趋于稳定，本文收敛速度较快。文献[14]改进算法和本文改进PSO算法收敛精度分别为5.33和4.42。可以看出本文改进的算法在收敛精度上更优。

将三种方法优化后的分数阶PID参数值进行阀门开度控制的仿真实验，取控制参数的平均值，在单位阶跃输入下得到控制效果如图7所示。

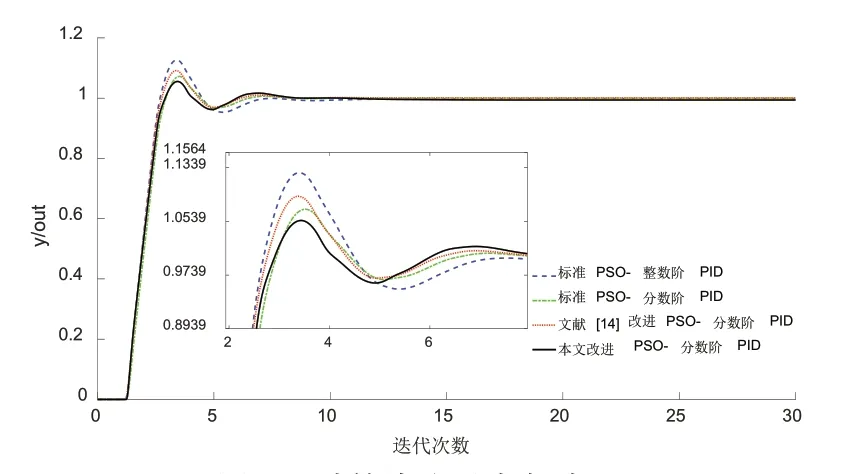
图7 三种算法阶跃响应对比

将四种算法的超调量、调节时间以及稳态误差三项控制指标性能对比，结果如表1所示。

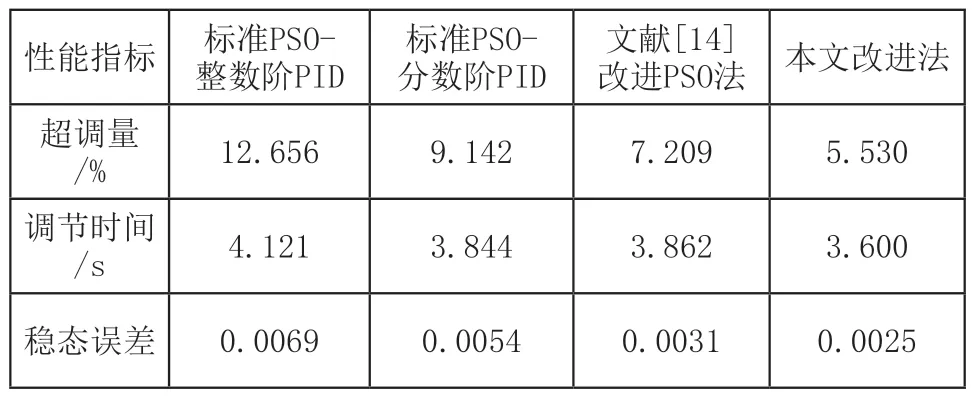
表1 四种算法性能指标

由图7和表1可以得出，本文改进的PSO优化分数阶PID算法超调量和稳态误差较另三种算法小，且调节时间最短。另外，根据表1也不难看出，分数阶PID较整数阶PID使系统有更优的动态性能。

在16s后，对内环施加幅值为0.1的阶跃扰动，系统的相应输出曲线如图7所示。

由图8看出系统在加入扰动后，本文提出的改进方法在受到扰动后可以更快速地恢复到稳态，有更好的抗干扰性。

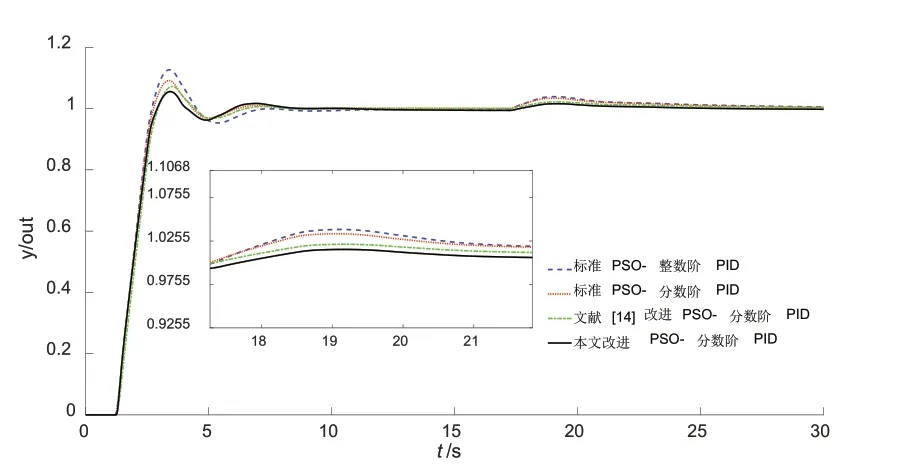
图8 不同算法的抗扰动曲线

5 结语

为提高阀门开度控制的精度，本文设计了分数阶PID控制器，采用阀门开度PIλDμ-气室气压P的串级控制思路，通过引入适应度值对惯性权值自适应调整，并综合迭代次数和适应度值选取学习因子，将改进的粒子群算法对Kp1，Ki，Kd，λ，μ和Kp26个参数优化。

仿真结果表明，对比标准PSO优化整数阶PID、标准PSO优化分数阶PID和文献[14]改进PSO优化分数阶PID这三种方法，本文改进PSO优化分数阶PID的调节时间快，超调量小，收敛精度更好，使控制系统具有较好的动态品质，为阀门开度控制研究提供了参考。