轴向激励弹性连接双刚性球低频声辐射计算及分析
赵腾瑞,伍先俊,孙红灵
(1.中国科学院噪声与振动重点实验室(声学研究所),北京 100190;2.中国科学院大学,北京 100049)
0 引 言
为了使结构在较大深度下满足一定的耐压强度,水下工程中常将结构分解成多个分散结构。大潜深的水下航行器一般采用多舱体结构,作用力激励舱体振动从而向外辐射声波。为使航行器有尽可能低的辐射噪声,需重点考虑舱体之间连接方式的设计。球舱作为一种耐压结构可以作为航行器舱体结构的一种形式,为使球舱在较大深度具有足够的强度,舱壁较厚,球壳越厚其固有频率越高,低频振动时一般只存在刚性模态,可忽略球壳本身的弹性,将球舱建模为刚性球,所以研究双刚性球不同连接方式下的辐射声场具有重要的应用价值。
辐射声场计算中的一个关键问题是多球体的散射,为方便利用每个刚性球表面的边界条件,需要将整个声场相对于每个球体中心展开,基本出发点是波函数的加法定理。1954 年,Friedman 和Russek[1]推导了一种任意阶球函数的平移加法公式,能将球函数平移到另一个球坐标系中表示,随后Stein 等[2]进行了修正;1962 年,Embleton[3]研究了平面波垂直球心连线入射时两刚性球之间的相互作用;1973年,Thompson[4]利用球函数的平移加法理论研究了轴对称简谐振速分布的辐射球源嵌入到一个较大的流体球内,并置于另一种无限大流体域中的声辐射问题;随后Thompson[5]又用同样的方法研究了辐射球源靠近一个散射球体的声辐射问题;1995 年,Gaunaurd 等[6]计算了平面波以任意角度入射被两个球散射后的声场,考虑了软边界和硬边界的情况,并计算了平面波入射下两球体系统的形函数;2003年,吴九汇等[7]利用格林函数的双中心球坐标展开式得到了一类球函数加法公式,基于该加法公式研究了两球体系统在不同边界条件下的散射声场;2014 年,张林根等[8]建立了近水面双圆柱壳的耦合声散射模型。
以上研究均为多体结构的声散射问题,也有学者研究了多体结构的声辐射问题。2016年,白振国等[9]基于模态叠加法提出了3个并排无限长弹性圆柱壳的振动声辐射耦合物理模型,计算了无限长线激励力作用在壳体时的辐射声场。随后他和胡东森等[10]又用该模型研究了3 个并排无限长弹性圆柱壳对平面声波的散射特性。上述研究中子结构之间不存在连接,彼此是相互独立的。本文以球舱为例,针对水下轴向激励的双刚性球振动模型,利用球函数的平移加法理论建立弹性连接两球舱辐射声场的解析解,基于该辐射声场的解析计算模型分析舱体之间连接方式和质量分布对辐射声场的影响。
1 理论分析
本章将对两个刚性球轴向振动产生的辐射声场进行理论推导,只计算100 Hz 以下刚性模态频段的辐射声场。整个辐射声场的计算大致可分为两个部分:首先是利用球函数的平移加法理论将各部分声压相对于每个球体中心展开成待定系数的形式,利用每个刚性球表面的边界条件得到关于声压待定系数的线性方程组,求解该线性方程组,将声压待定系数用两球轴向振动速度表示;第二部分是建立刚性球的动力学方程求解轴向振动的速度,其中关键的一点是求解流体对刚性球的反作用力,理论推导将从这两方面展开。
1.1 已知刚性球振速的辐射声场
如图1几何示意图所示,两个刚性球的球心沿z轴排列,半径分别为ra、rb。球心之间的距离为rab,z轴上两球最近两点之间的距离为dab,空间任意一点在两个球坐标系下的坐标分别为(r1,θ1,φ)、(r2,θ2,φ)。两球之间存在刚性连接或弹性连接,球A 受到沿z轴正方向的简谐激励力作用,两球沿z轴振动并向外辐射声压。将整个辐射声场分为4部分,分别为球A、球B振动的辐射声压pA、pB,球A不动时对球B 辐射声压的散射声压pASB和球B 不动时对球A 辐射声压的散射声压pBSA,具体表达如式(1)~(2)所示,式中省略了相同的时间因子ejωt。
式中,an、bn、asbn、bsan为待定系数,k为波数,hn(kr)为第二类球汉克尔函数,Pn( cosθ)为n阶勒让德函数。以球A为例分析刚性球沿z轴的振动,如图2所示,球A沿z的振动速度为va,则整个球面上的法向振动速度可表示为vr=vacosθ1=vaP1( cosθ1)。
利用球函数平移加法理论将不同坐标系下的声压表达式写到相同坐标系下。以球B振动辐射的pB(r2,θ2)为例,将其平移到球A所在坐标系中,则可用式(3)表达[4],其中jv(kr1)表示v阶球贝塞尔函数,p、v和n均表示求和阶数,N为截断阶数,p表示求和阶数,具体形式为p=n+v,n+v- 2,…,|n-v|。
其中,平移系数a( 0,0|p,v,n)表达式由式(4)给出。
用m替换v,同时调整求和次序,将式(3)写成更紧凑的式(5)。新的系数Bam是原待定系数的线性组合,Ba(m,n)表示矩阵Ba中第m行第n列的元素。
其中,αp= jm+p-n( 2m+ 1)a( 0,0|p,m,n)。同理可得其余声压平移之后的表达式(6)~(8)。
刚性球A、B 表面质点满足法向速度连续的边界条件,如式(9)~(10)所示,ρ0为水的密度,c0为水中声速。式(9)表示叠加后总声场在刚性球表面满足质点法向速度连续的边界条件,式(10)表示刚性散射条件,辐射声压与散射声压叠加后在散射球表面的质点法向振速为0。vma、vmb仅在m= 1 时不为0,其余阶数均为0。
将声压表达式代入式(9)~(10)化简可以得到N+ 1个形如(11)的线性方程组。
定义矩阵:
矩阵Ab(N+1)×(N+1)和Ba(N+1)×(N+1)中的第m行n列元素表达式如式(14)~(15)所示。
故刚性球表面的边界条件构成的线性方程组可用矩阵形式表示为
其中,系数矩阵S可表示为
待定系数向量可表示为
速度向量可表示为
由于刚性球只有整体沿轴向振动的速度,故求解方程(16)我们仅需系数矩阵逆矩阵中的两列。逆矩阵为S-1,其第2列、第N+1+2列分别为
声压的待定系数an可用两球振速表示为式(21),同理其它声压待定系数也可用相同形式表示。只要解得刚性球轴向振动速度即可确定声压待定系数从而确定整个声场。
1.2 水下球体动力学方程
为建立刚性球的动力学方程需要求解流体作用在刚性球上的力,这个力可由声压在刚性球表面的积分得到,以球A受到的反作用力为例,有
积分式(22)中对角度θ1的积分可表示为式(23),其中x= cosθ1。
计算积分式(23)需要用到勒让德函数的递推公式[11]:
利用勒让德函数的递推公式求解积分式(23)可得仅当m= 1 时积分不为0,其余阶数均等于0。故流体作用在两球上的力可用两球振速表示为
式中,系数I1、J1、I2、J2表达式由式(26)给出。
两刚性球的动力学方程如式(27)所示,其中ξa、ξb表示两球沿z轴的位移,K为刚度,F为激励力。
将流体对球的作用力代入动力学方程,求解线性方程组(27)可以解得刚性球的振动速度,将振速代入式(21)即可解得声压的待定系数an,用相同的方法可以解得其他声压的待定系数,从而确定整个声场。
本文以刚性球辐射的平均等效声源级作为衡量其声辐射的标准,平均等效声源级的定义由式(28)给出,其中“*”表示复数的共轭。等效声源级为声强在半径为rf的球面上的积分取对数,参考声功率Iref=8.37×10-18W表示的是距离点声源1m处声压幅度为1×10-6Pa的声功率。
2 算例分析
2.1 理论模型验证
为验证上述理论推导及建模的正确性,将理论计算与COMSOL 多物理场耦合计算软件的结果进行对比。所选择参数如下:刚性球密度ρA=ρB= 1000 kg/m3,刚性球半径ra=rb= 1 m,球心之间的距离rab= 2.1 m。两刚性球之间存在弹簧连接,弹簧刚度K=( 2πfa)2MaMb/(Ma+Mb),fa= 14 Hz 表示质量为Ma、Mb的质点与刚度为K的弹簧组成的双质点单弹簧系统在空气中的共振频率。球A 受到轴向力的激励,激励力的大小为F= 1 N。COMSOL 计算的流体域半径为15 m,结构有限元的单元最大尺寸为0.5 m,流体域网格最大尺寸为1 m,由于计算频率在100 Hz以下,声波波长大于15 m,满足一个波长内有6 个单元的条件。COMSOL 中激励力以及两刚性球之间的弹簧对两球的弹力均以点载荷形式施加在两球上,表示弹力的点载荷由弹簧弹力表达式给出。在半径rf= 10 m 的半圆周上选取若干场点,对比了有限元仿真和理论模型计算的场点声压幅值。图3(a)给出了频率为5 Hz各个场点理论计算与有限元仿真的声压幅度曲线,图3(b)则给出了单个场点θ= 0°在各频率点的声压幅度曲线。对比结果表明二者具有良好的一致性,说明了理论推导及建模的正确性。
2.2 双刚性球计算结果及分析
限定两个刚性球的总体积为40 m³,总密度为ρ=1000kg/m3,弹簧刚度K定义形式如前文所示,式中Ma与Mb相等,后续仿真时弹簧刚度保持不变。图4给出了两个刚性球体积和密度参数不同时弹性连接和刚性连接的等效声源级对比,体积和密度的具体参数由表1给出。由图4(a)~(b)两图可以看出,当两刚性球密度相同时,无论激励力作用在体积大的球上还是作用在体积小的球上,除峰值外两种连接方式的声源级基本一致,弹性连接并没有降低声辐射。由图4(c)~(d)两图可以看出,当两个刚性球的密度不同时,弹性连接时声源级除峰值点外还有一个谷点,在谷点处声源级较刚性连接有明显降低,本文称这个谷点为声场的抵消点。图4(c)是激励力作用在密度大的球上,此时声源级抵消点频率高于峰值点频率,并且在计算的100 Hz以内的频段,抵消点之后频率点的声源级相比刚性连接均有所降低。与此相反,图4(d)中激励力作用在密度小的球上,此时声源级峰值点频率高于抵消点频率,并且峰值频点之后的声源级相比刚性连接均有所升高。显然图4(c)中弹性连接的声源级曲线更符合降噪的要求,能在较宽的频率范围内降低声辐射,此时两刚性球密度要有差异并且激励力作用在密度大的球上。
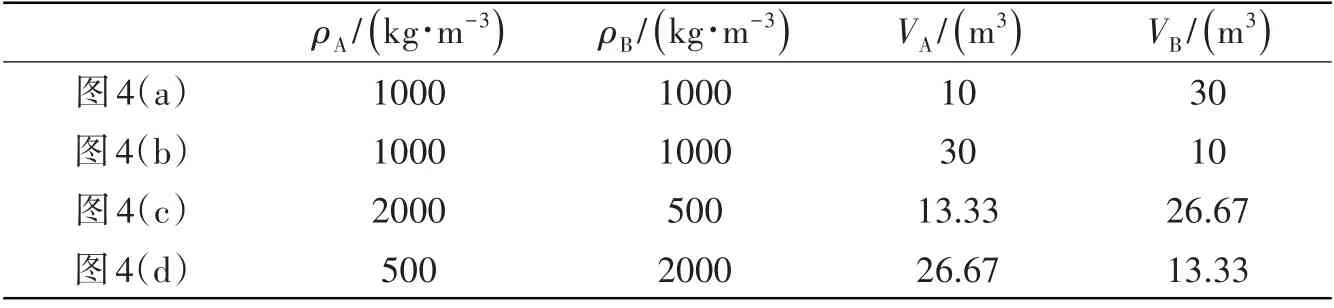
表1 图4中刚性球体积和密度参数Tab.1 Volume and density parameters of the rigid spheres in Fig.4
图5(a)~(b)分别表示图4(c)中两种连接方式在峰值频点处yz平面内各场点声压级,图6(a)~(b)分别表示图4(c)中两种连接方式在抵消频点处yz平面内各场点声压级。可以看出,在峰值频点弹性连接的各场点辐射声压相比刚性连接明显增加,在抵消频点弹性连接的两刚性球附近场点的声压有所增加,10 m之外的各场点声压明显降低。弹性连接的引入不仅改变了辐射声压的大小,而且改变了辐射声压的指向性。
为进一步分析声源级峰值点和抵消点产生的原因,比较了刚性连接和弹性连接时刚性球的振速。图7给出了表1中取图4(c)参数时弹性连接与刚性连接振速幅度比值随频率的变化曲线。表2给出了图7中两刚性球在声源级峰值点和抵消点处两刚性球弹性连接和刚性连接时振速比值。由图7 和表2 可知,声源级的峰值频率点即为两刚性球振速共振频率点,振速幅度显著增大。抵消频率点处两刚性球相比刚性连接的振速幅度比值均大于1,所以声源级的抵消点并不是由于刚性球振速减小造成的。

表2 图7中共振和抵消频率处振速比值Tab.2 Vibration velocity amplitude ratio at peak and canceled frequencies in Fig.7
图8给出了两个刚性球振速相位随频率变化的曲线。由图8可以看出,在峰值频点和抵消频点两个刚性球振速相位正好相差180°,振速相位相反使得两球振动辐射声压相位相反,叠加时相互抵消。从偶极子辐射角度理解,刚性球沿轴向振动时的辐射特性与偶极子基本一致,其辐射声压可用式(29)的偶极子形式表示[11]。
式中,Q1表示偶极子源的源强。忽略刚性球的声散射,轴向排列的双刚性球振动的辐射声场可近似等效为两个轴向排列偶极子的辐射声场。两球振速相位相反,等效为两偶极子源强相位相反,使得两偶极子辐射声压相位相反,叠加时相互抵消。在峰值频点两球振速显著增大,球A 振速小于球B 振速,两偶极子源强幅度相差较大,即使相位相反相互抵消,辐射声压依旧明显增加使得声源级存在峰值点。抵消点两偶极子源强幅度相近,叠加抵消后辐射声压显著降低使得声源级存在谷点。
以图4(c)中参数ρA= 2000 kg/m3,ρB= 500 kg/m3为例,计算了各个场点在抵消频率点的声压。图9(a)~(b)分别给出了在抵消频率点13.3 Hz处半圆周上场点各部分声压的实部和虚部。由图9可以看出,相比两个刚性球振动产生的辐射声压,刚性球的散射声压较小。图9(a)中两个刚性球辐射声压的实部在大部分场点符号相反,幅度略有差异,图9(b)中两刚性球辐射声压的虚部符号基本相反,幅度相近,两球辐射声压叠加时相互抵消,从而使得声源级出现一个谷点。图7中的振速曲线在共振频率点之后较宽频率范围内刚性球B弹性连接与刚性连接时振速幅度比均小于1,球B振速相比刚性连接减小,说明弹性连接起到了一定的减振作用。
2.3 近似分析探索
由于分析频率较低,考虑集中质量系统的近似,流体对刚性球的作用力以附加质量的形式体现。此时球A 的等效质量为Ma'=Ma+ρ0Vaβ,球B 的等效质量为Mb'=Mb+ρ0Vbβ。Ma、Mb为刚性球质量,Va、Vb为刚性球体积,β为流体附加质量系数。单个球轴向振动时,流体对刚性球的作用力可表示为式(30)的形式[11],其中r0为刚性球半径,v0为刚性球轴向振速。
低频时kr0<<1,h1(z)/(z)≈-z/2,作用力Fw可近似为式(31)的形式。其中Madd=ρ02πr03/3,流体附加质量系数β近似为0.5。根据文献[12]可知,在无界无黏流体情况下,半径为r0的球沿z轴方向运动时,球运动引起的附加质量等于排开流体质量的二分之一,这与本文的近似结果是一致的。
两刚性球作为集中质量系统的振动方程可表示为
球A、球B的振速表达式为
简谐振动刚性球的辐射声场就是偶极子声场[11],两球轴向振动的辐射声场用偶极子近似表示为式(34)的形式,双偶极子辐射几何示意图如图10所示。
式中,2d为两偶极子之间的距离,即两球球心之间的距离。由式(34)可以看出,当Qa与Qb符号相反时,两偶极子辐射声压相互抵消。
两偶极子源强比值的表达式为
低频时kra<<1,krb<<1,源强比值可近似为
对于辐射声压的抵消点,近似有Qa= -Qb,由式(36)解得辐射声场抵消点的角频率为
表3 给出了解析法和流体附加质量法计算得到的声场抵消点频率对比。可以看出,附加质量法得到的声场抵消点频率高于解析法得到的频率,由于附加质量法近似未考虑两球之间的相互作用,所以与解析法仍存在一定差异。

表3 声场抵消点频率计算Tab.3 Calculation of the canceled point frequency of sound field
由流体作用力表达式(25)可以看出I1、J1、I2、J2具有阻抗的量纲。I1、I2为两球的自辐射阻抗,J1、J2为两球的互辐射阻抗,将阻抗的实部与虚部分开表示为
将式(38)代入两球动力学方程中,可以得到
图11 给出了阻抗中的抗部分随频率的变化曲线。由图11 可以看出两球自辐射阻抗和互辐射阻抗中的抗部分符号相反。-jX11与jωMa符号相同,说明球A 的自辐射阻抗中的抗部分相当于质量抗,增加了球A的质量。-jX12与K/jω符号相同,说明球B对球A的互辐射阻抗中的抗部分为弹性抗,相当于对球A 有一个弹力作用。同理,球B 的自辐射阻抗中的抗是一个质量抗,互辐射阻抗中的抗是一个弹性抗。将流体等效近似为附加质量的集中参数系统,只考虑了球自辐射阻抗中的质量抗,并没有考虑球之间的互辐射阻抗,即没有考虑球之间的相互作用,因此与解析计算仍存在一定差异。集中质量系统近似无法解释球B的振动也存在极小值点。互辐射阻R21很小,-jX21与-K/jω符号相反,由式(39)的第二个式子可看出,当二者相加近似为0 时,球B 的位移与振速出现极小值点。空气中两球互辐射阻抗较小,几乎可以忽略,球B的位移与振速是不存在谷点的。
为分析互辐射阻抗对两球振速的影响,计算了两球间距离取不同值的情况。两球之间的距离为dab,选取频率为100 Hz 的声波波长λ=15 m 作为度量距离的标准。图12给出了两球距离不同时X11和X12随频率的变化。可以看出自辐射抗X11基本不随距离变化,而互辐射抗X12随两球之间距离的增大而减小,两球之间的相互作用减小。图13 给出了两球距离不同时振速幅度随频率的变化。球A 振速幅度基本不随距离变化,球B振速幅度的谷点随两球之间距离的增大逐渐向高频移动。当dab=λ时,100 Hz 以内已经看不到球B振速幅度的谷点了,而且距离越大,谷点也逐渐不明显了。
图14 给出了弹性连接两球间距离不同时声源级随频率的变化曲线,可以看出随着两球之间距离的增大,声源级的谷点逐渐升高,变得越来越不明显。从偶极子辐射角度容易理解,式(34)中两个偶极子总的源强可表示为
由式(40)可看出频率较低,两球距离较小时,sin(kdcosθ)相比cos(kdcosθ)很小,源强中起主导作用的是(Qa+Qb)cos(kdcosθ)。当两球反向振动,Qa与Qb符号相反,相互抵消后声源级能明显降低。随着距离的增大,sin(kdcosθ)和cos(kdcosθ)的差距变小,而Qa与Qb符号相反时,(Qb-Qa)sin(kdcosθ)是正向增大的,故声源级的谷点随两球间距离的增大会逐渐升高。
单个球轴向振动时的辐射声压可表示为
利用前述流体作用力的低频近似表达,可以得到辐射声压的近似表达式为
低频时kr0<<1,1/(kr0)≈(kr0)3/( -2j ),故式(42)可表示为
由单个球辐射声压的近似表达式(43)可以看出,单个球的辐射声压与球的密度ρ有近似反比的关系。激励力相同时,球密度越大,辐射效率越低,辐射声压越小。两球弹性连接时,力作用在密度大、辐射效率低的球上可以使辐射声功率较刚性连接有所降低。与此相反,力作用在密度小、辐射效率高的球上使得辐射声功率增加。
3 结 论
本文针对水下轴向排列双刚性球受轴向力激励振动的声辐射问题,利用球函数的平移加法理论,推导了辐射声场的解析解;计算了流体对刚性球的反作用力;建立了水下刚性球受轴向激励力振动的动力学方程,计算频率范围在100 Hz以内,比较了两个球弹性连接和刚性连接两种方式下的声辐射特性。本文的理论推导可以拓展到任意数量刚性球沿轴向振动产生的辐射声场。解析解能将各球辐射声压与散射声压分离,更容易分析辐射声场的特性,主要结论如下:
(1)弹性连接的引入使得刚性球振速存在相位相反的频段,刚性球的密度相同时,在两球振速相位相反频段两偶极子源强幅度相差较大,声源级只有峰值点(结构共振频率附近);刚性球密度不同时,在两球振速相位相反的频段存在两偶极子源强幅度相近的频点,声压相互抵消后使得声源级出现明显抵消点。与刚性连接相比,声源级抵消点可以达到多于10 dB的降噪量。
(2)总质量相同时,激励力作用在密度较大、辐射效率较低的刚性球时,声源级在抵消点之后的较宽频率范围内相比刚性连接均有所降低。激励力作用在密度较小、辐射效率较高的刚性球时,声源级在抵消点之后的较宽频率范围内相比刚性连接会增加。当平均密度与水相当时,在舱段的质量分布设计时可考虑将质量尽量集中在直接受激励力作用的舱段。
(3)非受力刚性球振速在共振点后较宽频率范围较刚性连接均减小,弹性连接起到了一定的减振作用。非受力球振速的减小也使得抵消点之后较宽频率范围内声源级均有所下降。
(4)采用流体附加质量和集中质量系统近似,得到了声压抵消频率的近似表达。附加质量的方法没有考虑两球之间的相互作用,因此得到的结果与解析方法存在一定的差异。
(5)两球之间的互辐射阻抗会随两球之间距离的增大而逐渐减小,球B 振速的谷点向高频移动,谷点逐渐变得不明显。声源级的谷点也会随两球距离的增大而升高,降噪量逐渐减小。

