一道中考压轴题的探索与变式
⦿湖北省宜昌市第六中学 李 玲
1 引言
解答一道复杂的数学题,以特殊情形为起点,往往能抓住数学问题的本质.现以2021年浙江省衢州市中考数学第24题解答探索及变式研究为例,探讨如何就题变式、就题借力,追寻解题教学初心,有效发展学生思维能力,力求解题教学效能最优.
2 试题呈现
推理:
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G.
(1)求证:△BCE≌△CDG.
运用:

图2
拓展:

3 解答研讨
3.1 “两等两线”看折叠,洞察结构得思路
思路分析:第(1)问,识别折叠具有轴对称的本质,洞察到“两等两线”结构:折痕BE所在直线既是∠FBC的平分线、也是对应点连线段CF的垂直平分线;还有全等三角形及等腰△BCF,△ECF这样的基本图形.执果索因,容易得到△BCE≌△CDG.
3.2 给定比值求线段,联想构造妙转化
第(2)问,在推理的基础上添加了线段比及一条线段长两个条件,紧扣“两等两线”如何去找关联?结合条件及图形分析,直接求解;或构建方程模型整体求解;或搜索关联相似三角形进行转化;或从直角入手建立坐标系,借助点的坐标去求线段长;或面积法入手建立方程等.


图3
思路一:由条件易求出EF,HF,HD的长度,从正方形内折叠的图形结构联想转化,想到双勾股法.

思路二:由图3中的对顶角和平行线,易得GH=FH=5,HD=4,再结合AB=BF=BC这个条件,在Rt△ABH中用勾股定理,先求出正方形的边长,再利用线段和差关系间接求DE的长.

解法2是从条件出发,顺思联想,从前一问找思路.这样的解答似乎还少了从设问间找关联,从结论出发逆推的思路.第(2)问还可以看透图形结构,求DE的长,由(1)易得GD=CE=EF,加上正方形易捕捉到AG=DE,从而在转化思想下,不妨直接设AG=DE=x,“由因导果、执果索因”,直取目标,计算上会优于解法2.
思路三:如图4,分别延长BH,CD交于点I,构造和DE有关的相似三角形,即△IDH∽△IFE,求出ID与IE的长.
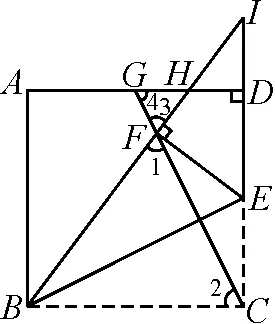
图4
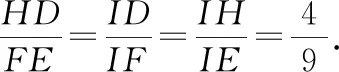

构造和DE有关的相似三角形有多种方法.结合图4,如,反“A”型△IDH∽△IFE,“A”型△IDH∽△ICB,“X”型△IDH∽△BAH,都可以求出DE的长,但在求解的过程中又引进了新的未知量,且计算的过程中同一个三角形三条边都需要用到,并涉及勾股定理,总的来说相似法计算难度较大.
思路四:建系,利用一次函数求出D,E的坐标.


图5

利用两点间的距离公式及FH=5找等量关系,理论上可求出t的值,但因为计算量大,在此处不追求解法的数量,仅供了解.
思路五:当图形中出现多处垂直,可以由垂直联想到高,进而联想到面积,用不同方法求同一个图形的面积就可以得到等量关系,常称作面积法.相较于前面4种解法,等量关系表面复杂,但计算并不复杂,计算难度较低,能顺利得到结果.
解法5:由给定条件易得DG=9,HD=4.如图3,设DE=x,由S梯HDCB=S△HDE+S△HEB+S△EBC,得


以上5种解法,学生最容易想到的思路是双勾股法、勾股、相似、建系,计算上最为简便的是解法1的双勾股法和解法5的面积法.笔者尤其要提到面积法难想易算这一点,启示我们无论做什么题,潜意识里不要见题就算,要先宏观选择方向,再微观确定方法.
3.3 形变质不变,类比迁移可得法
第(3)问,当“正方形”的条件换为“矩形”,比值的条件不变时,联系第(2)问的运用,发现问题表面上虽有变化,但在求解第(3)问时仍可沿用第(2)问的方法及思路.反过来,当把第(3)问的结果求出时,令k=1,利用第(2)问的结果来验证计算过程是否正确.沿用(2)的解题思路及方法,字母代替数,比值代替相等,体现了变化中的不变性.因此,从特殊到一般,可以帮助我们厘清思路,找到解题方法及问题的本质.



图6
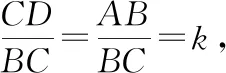
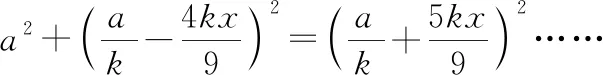
因为运算量大,勾股法在第(3)问中不适用,所以不做详细解答.同样,对于沿用第(2)问中的相似法、建系法,实际计算过程繁杂,都不适用于第(3)问.

点H在点D的右侧时,如图8,连接CH,仍设EC=x,则DG=kx.

图8
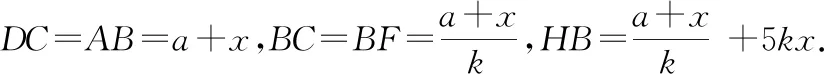

面积法的算式看起来非常复杂,但是化简计算过程非常简单.
4 变式拓展
结合以上解答探索,发现此题以正方形到矩形的折叠问题为探究背景,融入初中数学核心知识,渗透特殊到一般、数形结合、函数与方程、分类讨论等核心数学思想方法.若对试题相关的命题素材进行变式,将会引导学生注重知识体验的过程,优化学生思维方式,强化基本数学思想方法的感悟与内化,从而充分发挥此题的教学价值.基于此,笔者从以下三点进行了相关的变式思考.
4.1 第(1)问,还可以怎样设问?
能设问GD=EC吗?事实上,这种设问是可以的,而且比原题第(1)问证明△BCE≌△CDG的方法更多,例如三角函数法,也为第(2)问的解答提供更多线索和思路,这样的变式是可行的.
4.2 第(2)问,条件能更改吗?
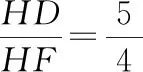
4.3 第(3)问,k值是任意的吗?
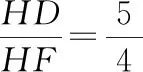
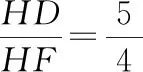

图9

图10

图11


图12

图13

图14

结合以上研题分析,给出这道题的完整变式,以进一步发展学生的思维,更好地落实本题的解题教学价值.
变式推理:
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连接BE,CF,延长CF交AD于点G.
(1)求证:GD=EC.
运用:
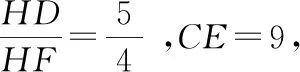
拓展:


