基于单元整体教学的作业设计与实施建议
——以“平行四边形”单元复习为例
⦿中山市东区松苑中学 张 青
1 问题提出
作业设计是初中数学教学中很重要的一个环节.作业分为课堂作业和课外作业,课堂作业是教学的载体,课外作业是教学活动的延伸.充分发挥作业的功能和价值,让“小小”的作业发挥“大大”的功能,对于减轻学生课业负担意义重大.“双减”背景下作业设计的转向由“零散”到“整合”,由“工具”到“发展”,从“随意”到“严谨”.以落实核心素养为导向,基于单元整体教学的作业设计应夯实基础,对“具有某种内在关联性”的内容进行重组、整合、设计,进而形成相对完整的单元教学作业,构建单元知识体系,实现教学效果最优化.
在初步学习“平行四边形”之前,学生已经学习了全等三角形、勾股定理等相关知识,本章的学习为后续几何知识的学习作铺垫,对于培养学生的逻辑推理能力意义重大.学生对平行四边形和特殊平行四边形之间的联系等容易混淆,为此从整体上设计本单元的作业,以激发学生的学习兴趣,发展学生的直观想象、逻辑推理等学科核心素养,帮助学生整体构建知识之间的联系.
2 作业设计依据
学习本章知识之前,学生已经熟悉了三角形和梯形的相关知识,了解了三角形的性质,掌握了特殊三角形的性质和判定方法、三角形全等的判定方法、勾股定理等相关数学知识,为本章学习奠定了知识基础.本节作业设计是单元复习作业,学生虽然初步了解了平行四边形的性质和判定方法,但是从整体上构建知识之间的联系较难,不能灵活运用相应知识解决数学问题.本章的学习也为后续二次函数、圆、相似等知识的学习奠定基础.
3 作业设计目标
立足教材,基于《义务教育数学课程标准》,从整体上设计本章节的作业设计目标:
(1)通过实践性活动,进一步探索平行四边形和特殊平行四边形的性质和判定方法,积累基本的数学活动经验;
(2)通过变式练习,发展数学思维,构建平行四边形之间的联系,培养学生逻辑推理能力;
(3)设计分层作业,由易到难,复习和巩固平行四边形的相关知识;
(4)创新作业形式,激发学习几何的热情,整体构建数学知识体系.
4 作业设计过程
4.1 立足基础,设计实践性作业,积累活动经验
作业1动手画两个全等三角形,并剪下来,将两个全等的三角形拼在一起,你能拼出什么四边形?并说说这个四边形的性质.
设计意图:从学生熟悉的三角形出发,让学生在“画一画”“拼一拼”“推一推”等数学活动中积累基本数学活动经验,体会不同类型的三角形可以拼成不同的平行四边形(如图1),由三角形的特殊性决定了平行四边形的特殊性.基于三角形的知识基础,从研究“特殊三角形”出发,引导学生从边、角、对角线等角度研究平行四边形的性质,让学生学会从一般到特殊的数学归纳方法.

图1
作业2推一推这些平行四边形的判定方法是什么?写一写它们之间的联系,并用思维导图的形式呈现出来.
设计意图:创新作业形式,通过构建思维导图,体会特殊平行四边形之间的区别和联系,从整体上把握“平行四边形”的相关知识,查漏补缺,培养逻辑推理能力.
4.2 着眼思维,设计变式练习,落实核心素养
练习1如图2,在矩形ABCD中,O为对角线BD的中点,过点O的直线分别与AD,BC相交于点E,F,连接BE,DF.
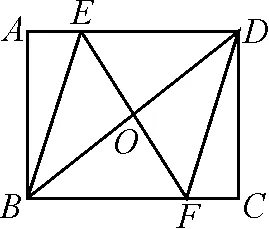
图2
(1)求证:四边形BFDE是平行四边形;
(2)若BD平分∠EBF,求证:四边形BFDE是菱形;
(3)在(2)的条件下,若BE平分∠ABD,求△ABE与矩形ABCD面积的比值.
变式如图3,ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,且AB=2.

图3
(3)分别过点C,D作BD,AC的平行线,交点为E,求证:四边形OCED为菱形;
(4)求四边形OCED的周长和面积.
设计意图:通过练习及变式,由浅入深,由易到难,进一步复习和巩固等边三角形的性质、角平分线的性质、平行四边形的性质和判定等知识.在构建平行四边形、矩形、菱形之间联系的过程中,培养逻辑推理能力;在完成作业的过程中,提升运算能力,让学科核心素养真正在完成作业过程中落地生根.
4.3 注重个体,设计分层作业,满足不同需求
A组练习:(1)在平行四边形ABCD中,对角线AC,BD交于点O,若使矩形ABCD成为正方形,添加的条件为______;若使菱形ABCD成为正方形,添加的条件为______.
(2)如图4,在矩形ABCD中,E是BC边上一点,∠AED=90°,∠EAD=30°,F是AD边的中点,EF=4 cm,则BE=______cm.

图4
B组练习:(3)如图5,四边形ABCD是矩形,E,F分别线段AD,BC上的点,点O是EF与BD的交点.若将△BED沿直线BD折叠,则点E与点F重合.

图5
①求证:四边形BEDF是菱形;
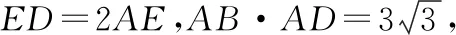
C组练习:(4)如图6,在正方形ABCD中,AB=2,E为边AB上一点,F为边BC上一点.连接DE和AF交于点G,连接BG.若AE=BF,则BG的最小值为______.
图6
设计意图:精心设计分层作业,让学生根据知识内容自主选择.分层作业并不是对学生进行分层,分层作业由易到难,基于学生的知识基础设置开放性问题.A组练习适合基础薄弱的学生.B组练习有利于学生思维能力的发展,进一步整体构建知识之间的联系.完成A组练习的学生有种成就感,巩固基础同时会进一步尝试B组练习.C组练习对学生的思维要求较高,可以通过小组合作交流共同完成.在师生交流互动的过程中领悟基本的数学思想方法,提升学生的竞争意识,激发学生学习数学的热情.
5 实施建议
5.1 作业设计“简约”而“不简单”
作业设计不仅仅是以传统练习的形式呈现,双减背景下的作业设计要求创新作业形式.教师可以坚持“零起点教学”,从学生熟悉的生活经验出发,设置“简约”的作业,让学生在“做一做”“画一画”“说一说”等数学活动中积累基本数学活动经验,轻松学习数学知识,让学生愿意学习数学.设计“简约”作业,要达到“不简单”的效果,让学生在掌握“四基”的同时发展“四能”,注重数学思想方法的渗透和核心素养的培养.
5.2 注重“整体性”和“典型性”
课堂作业是教学的载体,课外作业是教学活动的延伸.在作业设计的过程中,教师要充分挖掘例习题的功能和价值.作业设计的转向由“工具”到“发展”,由“零散”到“整合”,在作业设计的过程中注重目标的“整体性”,从整体的角度把零散的数学知识通过作业联系起来,构建数学知识之间的联系,从宏观的角度去开展作业设计.基于单元整体教学的作业按照“总—分—总”的思路进行设计,区分大单元、中单元、小单元之间的关系,作业设计注重“整体性”和“典型性”.作业不仅仅是“作业”,还承载着“教学”和“课程”的育人功能,作业设计要充分发挥作业的育人价值.
5.3 注重“层次性”和“差异性”
《义务教育数学课程标准(2022年版)》指出:“人人都能获得良好的数学教育,不同的人在数学上得到不同的发展.”[1]基于单元整体教学的作业设计应注重“层次性”和“差异性”,根据学生的知识基础和认知规律实施分层作业.分层作业依据学情及教学内容进行编制,由浅入深,由易到难,让所有学生都可以动笔写一写,增强学生学习数学的信心,激发学生学习数学的兴趣,让“人人都能学”“人人都愿学”.
5.4 改善评价方式,评价多元化
改进数学作业的评价方式,不以“分数”和“等级”作为唯一的评价方式.生动的激励语言可以激发学生的“内在潜力”,例如,“你的方法很不错”“这个图画得真好”等生动的作业评价语言,会带来不一样的效果.笔者尝试采用SK作业分析法,效果显著.S型错误指的是技能(Skill)缺失型错误,具体指学生因为审题错误、计算出错等导致没有做对;K型错误指的是知识(Knowledge)欠缺型错误,是指知识漏洞导致的出错.教师可以利用SK作业分析法,找出学生作业出错的真正原因,有针对性地设计作业,可以达到事半功倍的效果.

