构建相对运动模型 解天体“追及相遇”问题
王晓娜
(山东省平度经济开发区高级中学)
围绕同一中心天体在不同轨道做圆周运动的天体(或卫星),由于运动周期的不同,会出现相距最近或相距最远的情况,这类问题称为天体运动中的“追及相遇”问题.最近或最远外在表现为天体共线,其内在规律体现为天体运动过程中的角度关系或圈数关系.该类问题由于涉及两个物体的转动,其运动情境的构建和角度关系的寻找,对学生来说是一个难点.本文尝试从相对运动的角度,通过构建“圆周相对运动模型”,化多体运动为单一物体的运动,从而帮助学生有效突破这一难点,实现问题的快速求解.
1 引入圆参考系,构建“圆周相对运动模型”
如图1所示,物体A、B绕O点做同向(逆时针方向)匀速圆周运动,它们做圆周运动的角速度、周期分别为ω1、ω2和T1、T2.某一时刻,O、A、B共线,经时间t转过的角度分别为θ1、θ2.
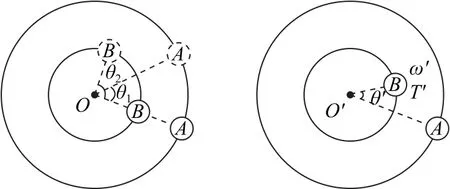
图1
假设ω2>ω1,则以OA连线为参考系,此参考系可称为圆参考系,在该参考系中,A可认为静止不动.则物体B相对角速度

相对转动周期
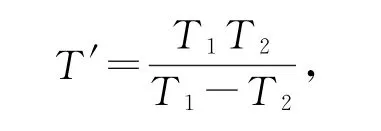
相对转过的角度
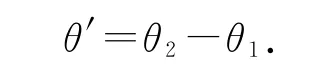
若物体A、B绕O点做方向相反的匀速圆周运动,如图2所示,则有
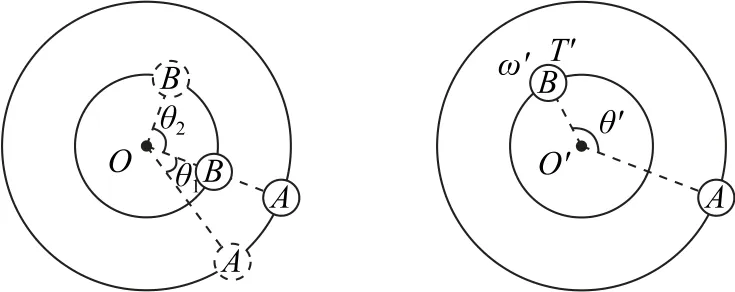
图2
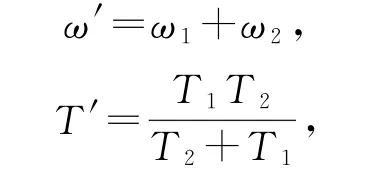
相互关系有

2 模型在天体“追及相遇”问题中的应用
2.1 同向运动星体的“追及相遇”问题
例1如图3 所示,天体a、b在万有引力作用下,绕中心天体c沿逆时针方向做匀速圆周运动,已知a、b轨道半径之比为ra∶rb=1∶4,则下列说法正确的是().
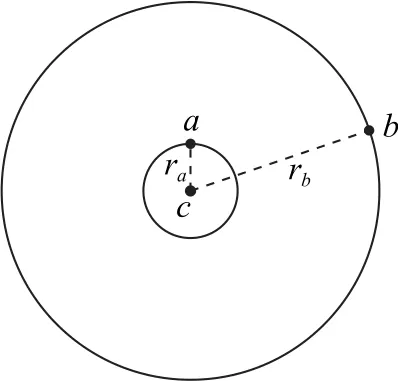
图3
A.a、b运动的角速度之比为ωa∶ωb=8∶1
B.a、b运动的周期之比为Ta∶Tb=8∶1
C.从图示位置开始在b转动一周的过程中,a、b相距最近7次
D.从图示位置开始,在b转动一周的过程中,a、b、c共线12次
解析由万有引力提供向心力,有
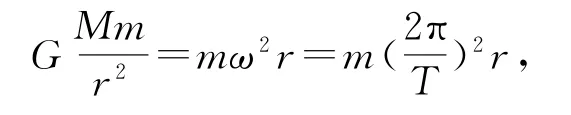
2.2 反向运动卫星的“追及相遇”问题
例2如图4所示,A、B两颗卫星绕地心O做匀速圆周运动,运动方向相反.A卫星的周期为T1,B卫星的周期为T2,在某一时刻两卫星相距最近,引力常量为G,则().
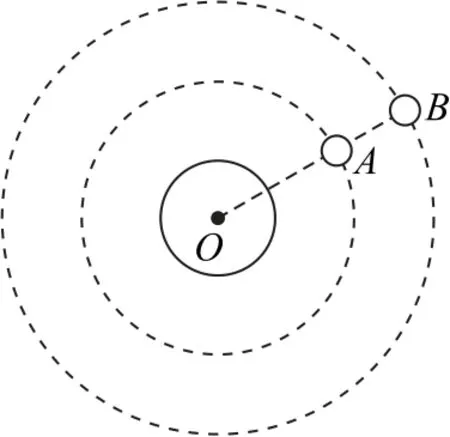
图4

若已知A、B两卫星相距最近时的距离,结合两卫星的轨道半径之比可以求出A、B两卫星的轨道半径,根据万有引力提供向心力,有则可求出地球的质量M,由于不知道地球的半径,故无法求出地球的密度,选项D 错误.
例3太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动.当地球恰好运行到某地外行星和太阳之间,且三者几乎排成一条直线的现象,天文学称为“行星冲日”.据报道,2014年各行星冲日时间分别是:1月6日木星冲日;4月9日火星冲日;5月11日土星冲日;8月29日海王星冲日;10月8日天王星冲日.已知地球及各地外行星绕太阳运动的轨道半径如表1所示.则下列判断正确的是().

表1
A.各地外行星每年都会出现冲日现象
B.在2015年内一定会出现木星冲日
C.天王星相邻两次冲日的时间间隔为土星的一半
D.地外行星中,海王星相邻两次冲日的时间间隔最短

在天体运动中,涉及相距最近或最远的时间问题和最近(最远)或共线的次数问题时,从相对运动的角度分析,通过建构“圆周相对运动模型”,可简化运动情境和减少运算量,有效突破学生的认知难点,切实提高学生解决问题的能力.
(完)

