赏析真实情境下抛体运动核心知识建构与问题解决策略
——兼谈2022年北京高考物理第17题一题多变
罗倩敏(特级教师)
(北京市第十八中学)
真实情境是指源于生活、生产、科技、实验、活动、学习等,能激发人兴趣,引起人联想,启发人思考,驱动人探究,并能在此过程中让人体会概念建构、规律探知、应用情怀、学习深入的一种资源,包括物理小故事、物理学史实、新闻报道、实物、图片、模型和影像资料等多种形式.抛体运动是一个经典的曲线运动模型,真实情境点多面广,是历年高考的热点问题.本文基于2022年北京高考物理第17题一题多变,谈谈真实情境下抛体运动核心知识建构与问题解决策略,以求抛砖引玉.
1 试题解析
原题体育课上,甲同学在距离地面h1=2.5m处将排球击出,球的初速度沿水平方向,大小为v0=8m·s-1;乙同学在离地面h2=0.7 m 处将排球垫起,如图1所示.垫起后球的速度大小不变,方向相反.已知排球质量m=0.3kg,重力加速度g取10 m·s-2.不计空气阻力,求:
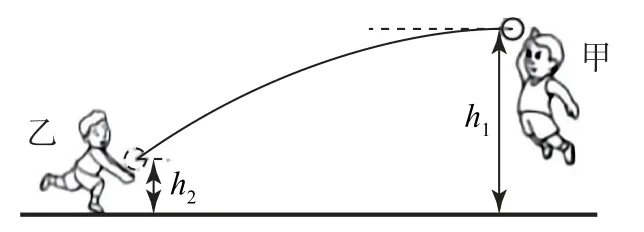
图1
(1)排球被垫起前在水平方向飞行的距离x;
(2)排球被垫起前瞬间的速度大小v及方向;
(3)排球与乙同学作用过程中所受冲量的大小I.
解析(1)排球在被垫起前做平抛运动,由运动的合成与分解知,水平方向上做匀速直线运动,则有x=v0t,竖直方向做自由落体运动,则有h1-h2=,联立两式代入数据解得x=4.8m.
(2)排球被垫起前瞬间,水平方向速度vx=v0,竖直方向速度vy=gt,合速度v==10m·s-1.
设速度方向与水平方向夹角为α,如图2所示,即tanα=,联立解得tanα=0.75,即α=37°.
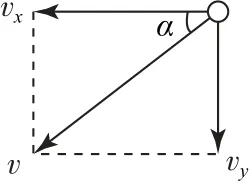
图2
(3)由动量定理可知,排球与乙同学作用过程中所受冲量等于排球动量的变化,已知被垫起后的排球速度(设为正方向)与垫起前大小相等方向相反,则有I=2mv=6kg·m·s-1.
点评试题取材于学生体育课上发接排球的真实情境.命题以曲线运动的“初末位置”为已知条件,通过“球的初速度沿水平方向”“垫起后球的速度大小不变,方向相反”“重力加速度g取10 m·s-2,不计空气阻力”等关键信息,设问了水平位移、末速度及排球和乙同学作用过程中所受的冲量3个问题,考查了平抛运动的模型建构——排球以水平初速度被击出,运动中只受重力作用;平抛运动的概念建构——位置、位移、初速度、末速度、加速度;平抛运动的规律建构——运动的合成与分解,以及力与运动关系在不同过程中的体现.集中反映了从描述性知识(平抛运动描述的物理量)到结构性知识(平抛运动模型),再到解决问题策略(分运动与合运动的等效性、等时性、独立性,牛顿运动定律与动量定理),可谓认知进阶自然,给人一种考试中再学习的感受,体现了人文关怀之情.
2 一题多变
2.1 描述性知识建构
变式1在原题基础上,若乙同学垫起排球过程用时为t=0.1s,球在竖直方向上发生位移为h=0.05m.
(1)排球被垫起过程中的v-t图像哪个正确?
(2)求乙同学对排球的平均作用力ˉF的大小(保留小数点后面一位数字);
(3)若排球被垫起的过程中加速度的方向与v始终同在一直线上,那么乙同学对排球的作用力如何变化?
(4)求乙同学对排球做功的平均功率ˉP.
解析(1)根据弹力与形变关系可得,形变大,弹力大,因此,球受乙同学的作用力是不断变化的,球的加速度也是不断变化的.所以球在被垫起的过程中先是加速度向下减小到零,速度逐渐增大至最大.然后,加速度向上增大,速度逐渐减小到零,再是加速度方向不变逐渐减小到零,速度反向向上逐渐增大到最大,最后加速度反向向下增大,速度减小,直到离开乙同学.故图3-丁正确.
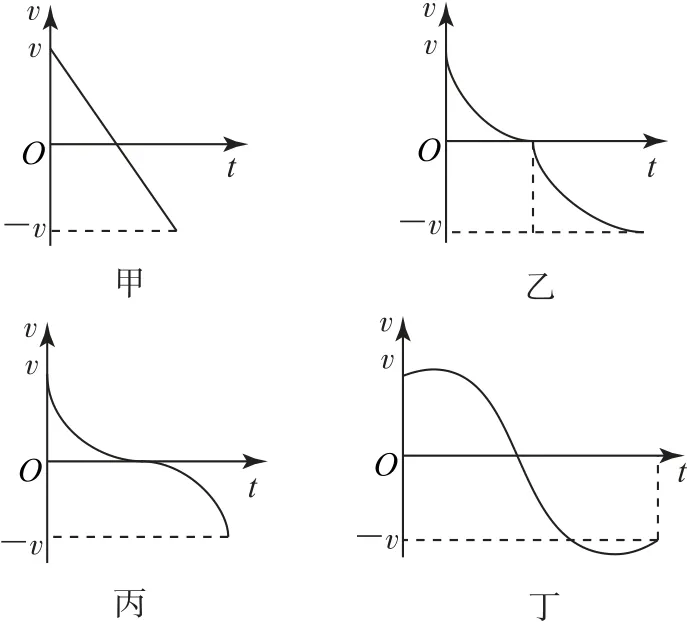
图3
(2)对排球,在被垫起过程中的受力分析如图4所示,由定义式得=200.0 m·s-2.由平行四边形定则得力的合成图如图5所示,根据余弦定理可得,

图4
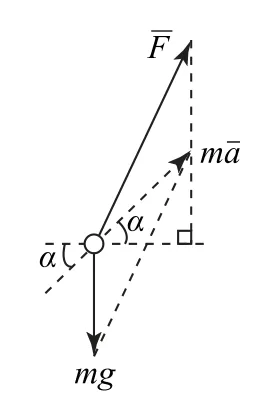
图5
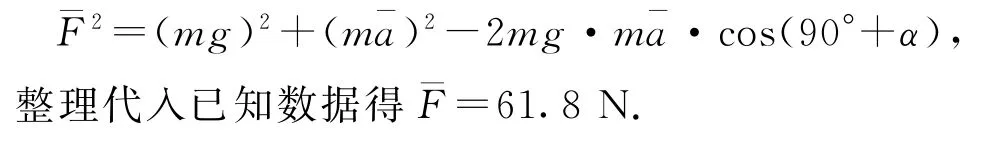
(3)对排球,由于所受重力不变,加速度方向始终与速度在同一直线,于是根据平行四边形定则,作出球在被垫起过程中的动态受力分析如图6所示.即乙同学对排球的作用力由零突然增大,直至等于重力大小,方向竖直向上(加速度为零,速度斜向下达最大),接着作用力继续增大,使球的加速度反向并增大,速度逐渐减小直至为零,然后作用力减小,加速度减小,速度反向(斜向上)逐渐增大,直至作用力再次与重力平衡,速度达最大,接着作用力变小,使球的加速度反向增大,直至乙同学对球作用力为零而迅速分离,详情可对照(1)问中图3-丁分析.
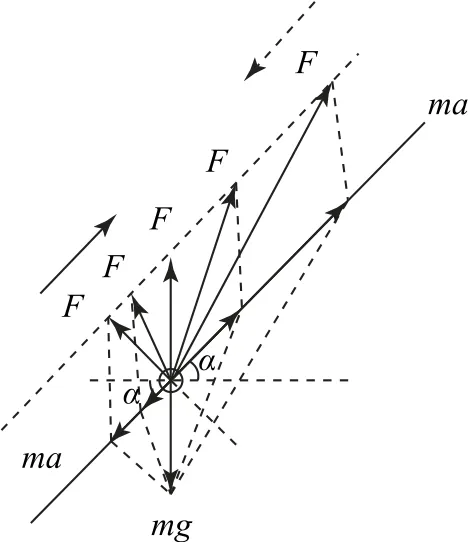
图6
(4)对排球,在被垫起过程中,由动能定理得ˉPtmgh=ΔEk,由已知得=1.5 W.
点评试题以排球被垫起过程为情境,考查了基于力与运动的力、加速度、速度、功、功率等关联概念的描述性知识建构,基于物理量关联的牛顿运动定律、力的合成与分解、动能定理等规律性知识建构,以及基于规律应用的v-t图像、平行四边形定则、数理思维等解决问题的策略.
2.2 结构性知识建构
变式2在原题基础上,连接甲乙同学发接球两点所在的直线AB,如图7所示,对于排球自甲同学水平击出到乙同学接到之前的过程.试论证:

图7
(1)排球速度的变化与其所花时间的比(速度的变化率)为定值;
(2)重力作用的冲量大小IG与重力作用的瞬时功率PG之比是定值;
(3)若甲同学水平击出排球的速度小于或等于8m·s-1时,排球落在直线AB上的速度方向是相同的;
(4)设计一个实验方案,说明平抛运动可分解为水平方向的匀速直线运动和竖直方向的匀加速直线运动.
解析(1)由定义可知a=,由牛顿第二定律知=g,联立两式得=g,故排球速度的变化与其所花时间的比(速度的变化率)为定值.
(2)对排球,下落过程中重力作用的冲量大小IG=mgt,重力作用的瞬时功率PG=mgvy=mg2t,联立得为定值.
(3)如图8所示,建立直角坐标系,设AB与水平方向成夹角θ,由运动的分解得x=v0t,y=,tanθ=,联立解得tanθ=,排球落在AB线上,将其速度分解,如图8所示,tanα=,联立得tanα=2tanθ.当水平初速度小于8m·s-1时,只是落到AB上的位移减小,位移方向是不变的,故排球落在直线AB上的速度方向是相同的.

图8
(4)用频闪(设频率为f)照像法记录排球的运动,通过照片中的各球分别作水平线和竖直线,如图9所示,只要验证在误差允许范围内,相邻两球在水平方向位移满足,竖直方向上位移差满足Δy=,即可证明平抛运动可分解为水平方向的匀速直线运动和竖直方向的匀加速直线运动.
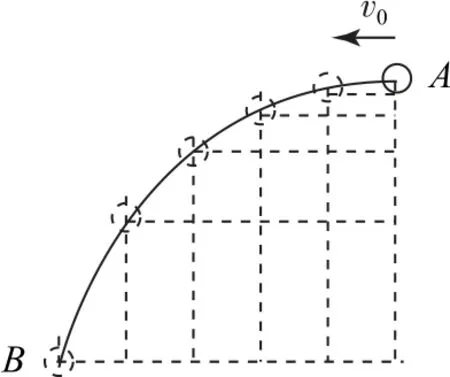
图9
点评试题以排球水平抛出为情境,考查了速度、速度的变化与其所花时间的比(速度的变化率)、冲量、功率、实验设计等关联平抛运动的结构性知识建构,基于抛体运动关联的运动合成与分解、匀变速直线运动、牛顿运动定律等规律性知识建构,以及基于规律应用的数理思维、实验设计思维等解决问题的策略.
2.3 探究性知识建构
变式3在原题基础上,请问:
(1)排球被垫起后其速度延长线是否平分排球被垫起前的水平位移x? 排球能否水平回到甲同学手上? 试论证你的结论;
(2)写出排球返回甲同学过程中的运动轨迹方程,并说明排球在上升过程中,速度是如何改变的;
(3)研究曲线运动可以“化曲为圆”,在曲线上任意取一小段看成一个圆周运动的一小部分,试分析排球上升过程中的曲率圆半径如何变化.
解析(1)排球被垫起后其速度延长线平分排球被垫起前的水平位移x,且能水平回到甲同学手上.排球被垫起后建立直角坐标系如图10所示,由运动合成与分解可知,排球在水平方向上做初速度为vx0=vcosα=8m·s-1的匀速直线运动,竖直方向做初速度vy0=vsinα=6m·s-1、加速度为g=10m·s-2的匀减速直线运动,即vy=vy0-gt,令vy=0,联立得t=0.6s.在该过程中球的水平位移为x=v0t=4.8m,竖直位移为y=vy0t-=1.8 m.联立解得球历时0.6s到了最高点,且以8m·s-1速度水平回到了甲同学手上.由几何关系得,排球被垫起后其速度延长线交甲同学水平击球延长线于Q点,由几何关系得tanα=则x′==2.4m,结论得证.
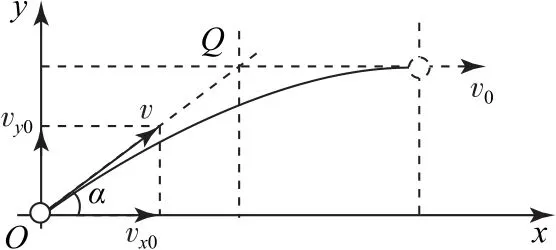
图10
(2)如图10所示,由运动合成与分解得x=v0t=8t,y=vy0t-=6t-5t2,联立两式得排球运动的轨迹方程为,即为曲线运动.同理得球在任意时刻的速度大小为
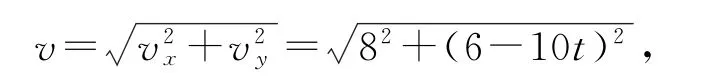
速度方向与水平方向夹角为
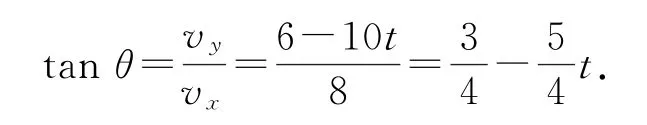
可见,排球在上升过程中的速度大小逐渐变小,速度方向与水平夹角逐渐减小.
(3)过排球被垫起的一小段曲线做速度为v的内切圆,切点为球的被垫起点,如图11所示,将重力加速度沿垂直速度v指向圆心方向分解得向心加速度an,由矢量分解及几何关系得an=gcosα,由圆周运动规律得曲率半径ρ=,而球到最高点时,同理作曲线内切圆,可得曲率半径为

图11

可见,排球在上升过程中,曲率圆半径在逐渐减小.
点评试题以排球被垫起后做抛体运动为情境,考查了位移、轨迹、速度等关联平抛运动的探究性知识建构,基于抛体运动关联的运动合成与分解、匀变速直线运动、圆周运动等规律性知识建构,以及基于规律应用的逆向思维、化曲为圆、等效思维、数理思维等解决问题的策略.
总之,2022年北京高考物理第17题及其一题多变是关于抛体运动、接发排球等真实情境下的综合问题,可以综合考查基于力与运动的描述性、结构性、探究性等核心知识建构和关联曲线运动的规律性知识建构,以及基于规律应用解决真实情境问题的应对策略.启发考生面对真实情境问题时,要从描述性物理量入手,建构运动模型,将运动分析、受力分析结合起来,选择牛顿运动定律、运动的合成与分解、匀变速直线运动、圆周运动、动量定理、动能定理等规律,应用v-t图像、等效思维、逆向思维、化曲为圆、数理思维、守恒思想、实验设计思维等解决问题策略,方能使问题迎刃而解.
(完)

