排球平抛运动的临界模型
康宝龙
(甘肃省合水县第一中学)
在学习平抛运动时,我们经常碰到以排球做平抛运动为背景的习题,其中排球的两类临界问题是平抛运动学习的难点.下面我们就对这两类临界问题加以例析总结,以期读者能更好地突破该难点.
1 临界速度的计算——球既不触网又不出界
如图1所示,击球高度为h1,球网高度为h2,击球点到球网及球网到边线的水平距离分别为s1和s2,要使球既不触网又不出界,求水平有效击球的速度范围.
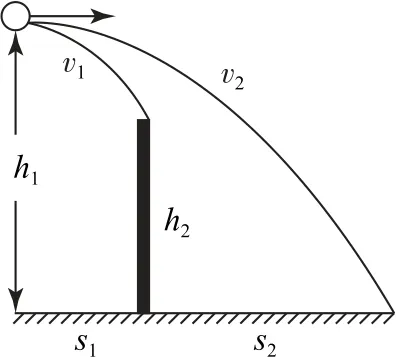
图1
1)从网上擦过的临界速度v1的大小计算.水平方向s1=v1t1,竖直 方向h1-h2=.两式联立解得v1=s1

在高度h1处有效发球的速度范围是
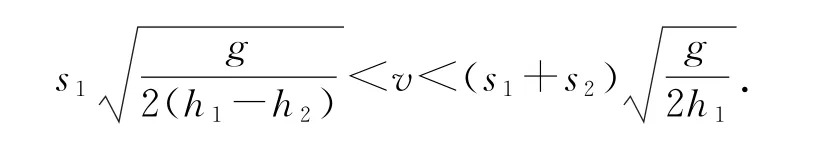
例1如图2所示,某学校的排球场长为18m,球网高度为2 m.一同学站在离网3 m 线上(虚线所示)正对网竖直跳起,并在离地高2.5 m 处将球向正前方水平击出.不计球飞行过程中受到的阻力,g取10m·s-2,欲使球既不触网又不出界,则击球速度可能是().
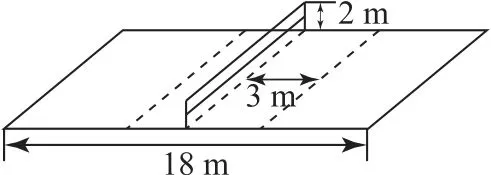
图2

2 临界高度的计算——球不是触网就是出界
如图3所示,当击球点的高度h1为何值时,无论水平击球的速度多大,球不是触网就是出界.


图3
例2如图4所示,排球场总长为18m,设网的高度为2 m,运动员站在离网3 m 远的线上正对网前竖直跳起,在高为2.5 m 处把作为质点的排球垂直于网水平击出.(空气阻力不计,重力加速度g取10m·s-2)则().
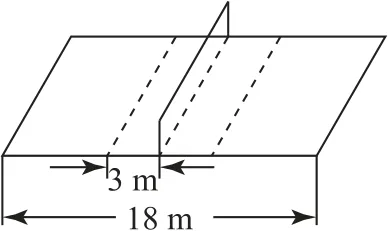
图4
B.击球速度大于20m·s-1,球必定会出界
C.击球速度小于10m·s-1,球必定会触网
D.只要击球点高于2m,且击球速度合适,球总可以落到对方界内
解析如图5所示,排球恰好不触网时其运动轨迹为Ⅰ.排球恰好不出界时其运动轨迹为Ⅱ,根据平抛运动的规律,排球恰好不触网时有x1=3m=v1t1,h1=2.5m-2m=,解得排球飞行时间·s-1≈9.5m·s-1.

图5
当排球恰好不出界时有x2=3 m+9 m=v2t2.h=2.5 m =,可解得m·s-1≈17m·s-1,故选项A、B正确,选项C错误.
如图6所示为排球恰好不触网也恰好不出界的临界轨迹.设击球点高度为h,根据平抛运动的规律有
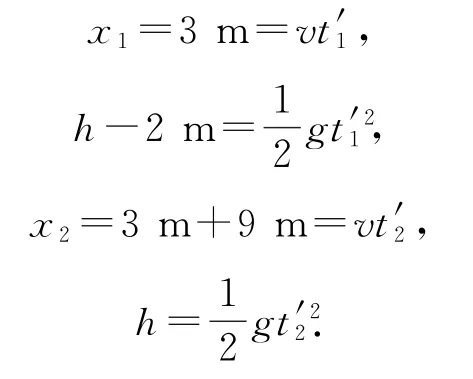
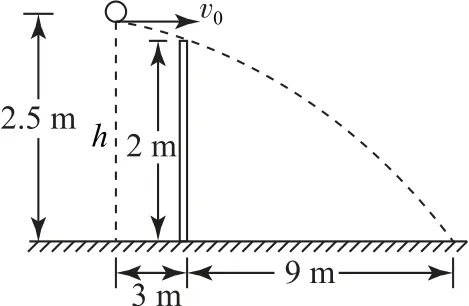
图6
联立以上四式可得h=2.13m,故选项D 错误.
例3如图7所示是排球场地的示意图.排球场ABCD为矩形,长边AD=L=18 m,前场区的长度为,宽L2=12m,网高为h=1.95m.在某次排球比赛中,若运动员在底线AB中点P的正上方跳起水平发球,当排球进入对方半场的后场区域时才算有效,忽略空气阻力,排球可看作质点,下列说法正确的是().
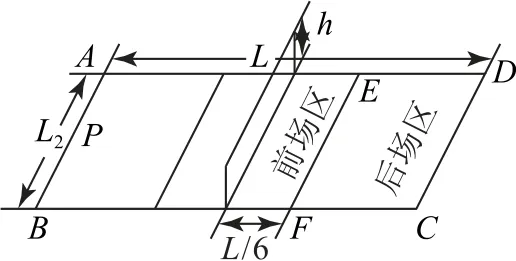
图7
A.若运动员的击球点高度为3.20m,有效击球的最小速度为18m·s-1
B.若运动员的击球点高度为3.20 m,有效击球的最大速度为22.5m·s-1
C.若沿垂直AB方向水平击球,击球点高度小于2.6m,则发球必定失败
D.若沿PD方向水平击球,击球点高度高于2.6m,只要速度合适,发球可以成功
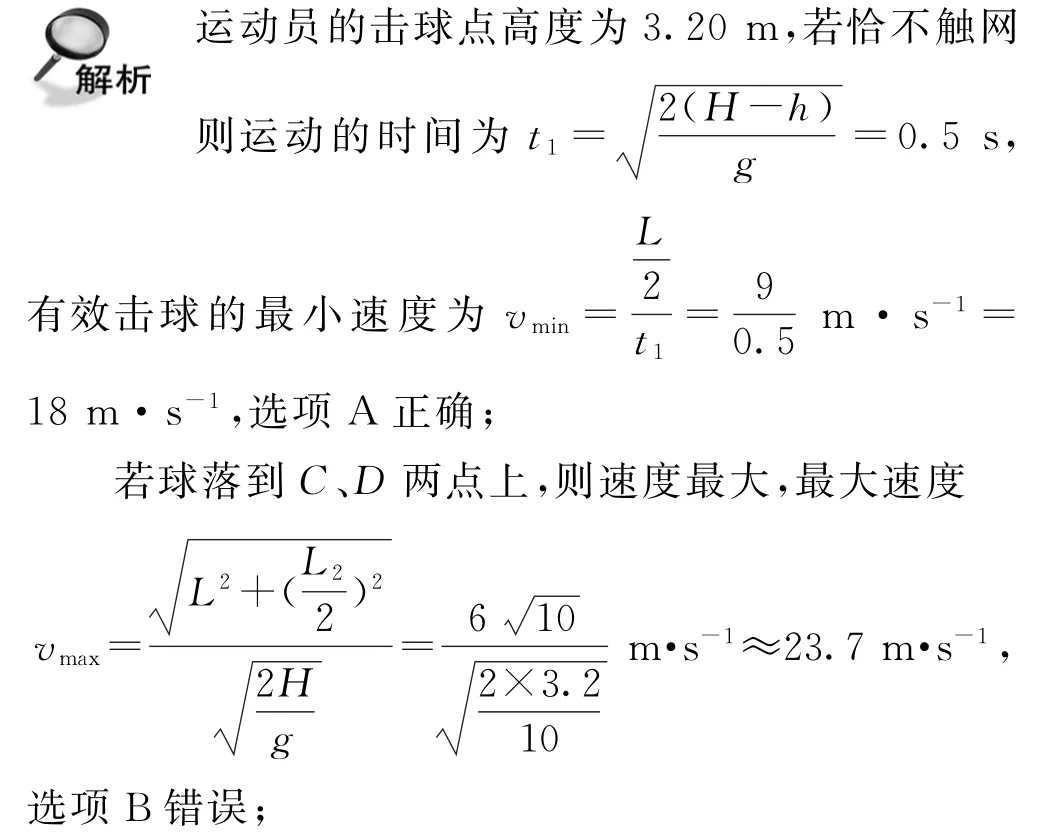
若沿垂直AB方向水平击球,打到触网点与打到CD线时间之比为1∶2,则下落高度之比为1∶4,所以临界高度与网高比为4∶3,则临界高度为H0==2.6m.则若沿垂直AB方向水平击球,击球点高度小于2.6m,发球一定会失败,选项C正确;
若沿PD方向水平击球,击球点高度大于2.6m,只要速度合适,发球可以成功,选项D 正确.
总之,在解答排球类试题的两类临界问题时,首先确定题目是临界速度问题,还是临界高度问题,然后画出排球的临界轨迹,根据临界轨迹,列出水平方向和竖直方向的方程,消去时间“t”,即可求解.
(完)

