圆锥摆“形变”记
涂剑涛
(河南省沈丘县第二高级中学)
圆锥摆是圆周运动知识板块中的重要模型之一,也是高考考查的重要知识点.在高考中,对于圆锥摆的考查,常常以圆锥摆原模型为“本”,进行形变、演化,从而考查考生对知识的应用能力.下面,我们先回顾一下圆锥摆的“本”.
圆锥摆模型长为l的轻绳一端拴有质量为m的小球,另一端固定,小球在水平面内做匀速圆周运动,轻绳与竖直方向的夹角为θ.
分析我们对小球进行受力分析,如图1 所示,小球做圆周运动的轨道半径r=lsinθ,小球运动轨道平面到悬点的距离h=lcosθ,小球做圆周运动的向心力
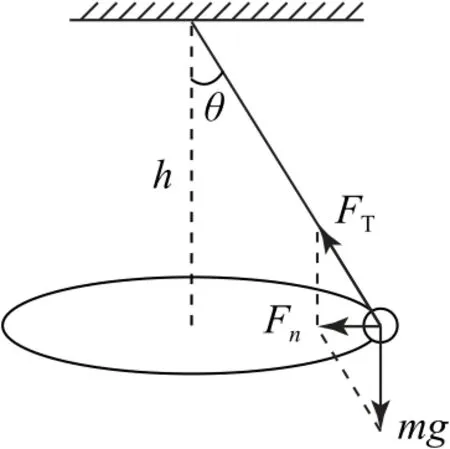
图1

回顾完了圆锥摆模型的“本”,我们就以两道试题为例,探究圆锥摆两类重要形变.
变形1 双绳类圆锥摆
1)如图2所示,两轻绳拴着小球在水平面内绕竖直杆AB做匀速圆周运动,长度为l的轻绳AC与竖直方向的夹角为θ,要求BC一直水平拉直,当绳子BC拉力等于零时,小球的角速度最小,有mgtanθ=,解得ω0=.角速度由ω0增大的过程中,因为绳AC上的拉力在竖直方向的分量等于重力,故绳AC上的拉力大小不变,绳BC开始有拉力,并由零开始逐渐增大.
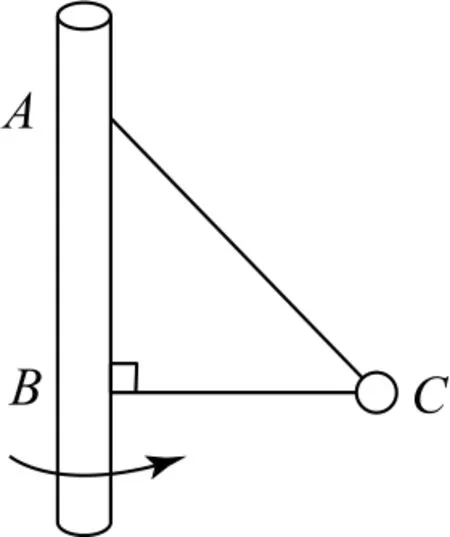
图2
2)如图3所示,竖直轻绳a和水平轻绳b拴着小球在水平面内绕竖直杆BC做匀速圆周运动,小球的角速度由零逐渐增加的过程中,因为绳a上的拉力大小等于mg,故绳a拉力大小不变;绳b上的拉力充当向心力,随着角速度的增加,绳b上的拉力逐渐变大.
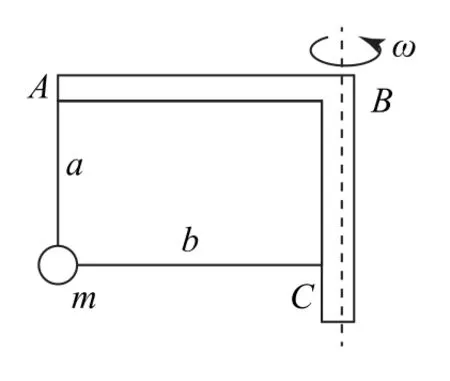
图3
3)如图4所示,两轻绳在水平方向的分力之和充当向心力;竖直方向的分力与重力的合力等于零.

图4
例1如图6所示的离心装置中,光滑水平轻杆固定在竖直转轴的O点,小圆环A和轻质弹簧套在轻杆上,长为2L的细线和弹簧两端分别固定于O和A,质量为m的小球B固定在细线的中点,装置静止时,细线与竖直方向的夹角为37°,现将装置由静止缓慢加速转动,当细线与竖直方向的夹角增大到53°时,A、B间细线的拉力恰好减小到零,弹簧弹力与静止时大小相等、方向相反.重力加速度为g,取sin37°=0.6,cos37°=0.8,求:

图5
(1)装置静止时,弹簧弹力的大小F;
(2)环A的质量M.
解析(1)设装置静止时AB、OB的张力分别为F1、F2,对A有F=F1sin37°,对B有
F1cos37°+F2cos37°=mg,F1sin37°=F2sin37°,解得F=.

变形2 有支持力、摩擦力参与的类圆锥摆
1)如图6所示,小滑块与粗糙的斜面一起绕着转轴BC在水平面内做匀速圆周运动,则有:a)小物块受到的沿斜面向上的静摩擦力与支持力在水平方向的分力充当向心力;b)小物块受到的沿斜面向上的静摩擦力、支持力、重力在竖直方向的合力等于零;c)随着角速度的增加,小物块受到的静摩擦力越来越大,支持力越来越小,当静摩擦力达到最大值时,小物块将做离心运动.

图6
2)如图7所示,小球在粗糙的漏斗内壁做匀速圆周运动.a)当小球的角速度ω=时,小球与漏斗内壁没有摩擦力;b)当小球的角速度ω>时,小球与漏斗内壁之间有沿着斜面向下的静摩擦力,并随着ω的增大而增加,斜壁支持力随着ω的增加而增大;c)当小球的角速度ω<时,小球与漏斗内壁之间有沿着斜面向上的静摩擦力,并随着ω的增大而减小,斜壁支持力随着ω的增加而增大.
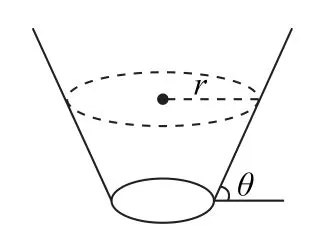
图7
例2如图8所示,倾角θ=53°的斜面ABC固定在可以绕竖直轴转动的水平转台上,斜面最低点A在转轴OO1上.转台以角速度ω匀速转动时,将质量为m的小物块(可视为质点)放置于斜面上,经过一段时间后小物块与斜面一起转动且相对静止在AB面上,此时小物块到A点的距离为L.已知小物块与斜面之间动摩擦因数为0.5,重力加速度为g,若最大静摩擦力等于滑动摩擦力,取sin53°=0.8,cos53°=0.6.则物块相对斜面静止时().

图8
A.小物块受到的摩擦力方向一定沿斜面向下
B.小物块对斜面的压力大小不小于mg
C.水平转台转动角速度ω应不小于
D.水平转台转动角速度ω应不大于
解析当角速度较小时,小物块有沿斜面向下的运动趋势,受到的摩擦力方向沿斜面向上,选项A 错误;当角速度最小时,物块恰好不下滑,受力分析如图9所示,根据平衡条件有FN1cosθ+Ff1sinθ=mg,Ff1=μFN1,FN1sinθ-Ff1cosθ=,解得ω1=,FN1=mg.

图9
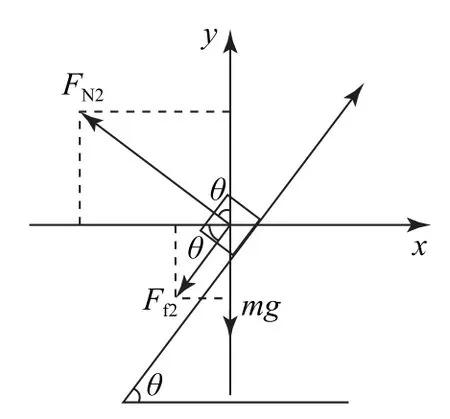
图10
当角速度最大时,物块恰好不上滑,受力分析如图10所示.根据平衡条件有FN2cosθ=Ff2sinθ+mg,Ff2=μFN2.x轴方向有FN2sinθ+Ff2cosθ=,解得ω2=,FN2=5mg.由以上分析可知,角速度取值范围为.小物块对斜面的压力大小=FN,取值范围为mg≤≤5mg,故选项B、C正确.
在解答圆锥摆类题目时,要对做圆周运动的物体的受力情况分析清楚,不漏力、不添力,并注意随着角速度的变化,拉力、支持力的大小都会发生变化,静摩擦力不仅大小变化,方向也可能发生变化,在解题时,要注意分析这些变化.
(完)

