构建“竖直上抛运动”模型 巧解追及相遇问题
李京军 牛金鑫
(山东省淄博市临淄中学)
追及相遇是日常生活中一类比较典型的运动问题,也是学生学习的一个难点.学生在分析此类问题时,常会在寻找物体间的位移关系、时间关系和速度关系的过程中,顾此失彼,错误频出.其实,认识到运动的相对性,以其中一个物体为参考系,通过构建“竖直上抛运动”模型,可使该类问题的求解过程简洁明快,达到事半功倍的效果.下面结合例题进行说明,以期能够对读者有所启发.
1 模型构建
1.1 问题情境
为了打击超载、超速、酒驾等违法行为,在成都的三环路川蒙立交路段,一辆值勤的警车停在匝道边督查车辆超速、超载情况.当警员发现从他旁边有一辆匀速行驶的货车严重超载时,立即启动警车去追赶,假设超载货车的速度为v0=54km·h-1,警车做加速度大小为a=5m·s-2的匀加速直线运动,不计警员的反应时间和警车的启动时间.
(1)警车追上超载货车前,两车相距的最远距离为多少?
(2)警车启动后多长时间追上超载货车?
分析这是一道常见的水平方向的追及相遇问题,常见的求解方法有过程分析法、解析法、图像法等.在运用常规思路进行求解时,学生往往会在位移关系的寻找、函数关系的解析和运动图像的转换中出现诸多问题.
有没有其他的分析方法,可避免这些问题的出现呢?
1.2 运动类比
1)竖直上抛运动特点
竖直上抛运动的初速度v0竖直向上,加速度为重力加速度g,方向竖直向下,其运动性质为有往复的匀变速直线运动;运动过程包含匀减速上升和匀加速下降两个对称的过程,如图1所示.
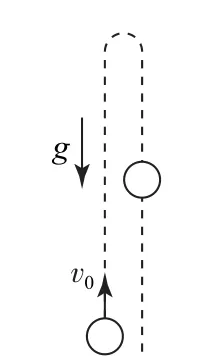
图1
2)警车相对货车的运动特点
以货车为参考系,警车具有水平向左的初速度v0和水平向右的加速度a,其相对货车的运动性质亦为有往复的匀变速直线运动.运动过程包含向左匀减速和向右匀加速两个对称过程,如图2所示.
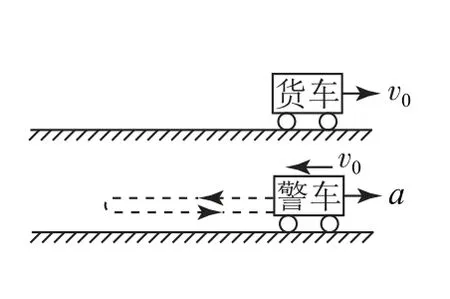
图2
1.3 建构模型
通过前面的类比分析不难看出,警车相对货车的运动与竖直上抛运动的运动性质和遵循的运动规律是相同的.这里通过巧选参考系,从相对运动的角度可将警车的运动转化为“竖直上抛运动”.注意模型构建后所涉及的位移、速度和加速度均为相对位移、相对速度和相对加速度.
1.4 解决问题
(1)警车运动到“竖直上抛运动的最高点”时,两车相距最远,最远距离
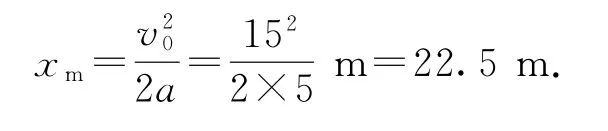
(2)警车返回到“竖直上抛运动的初始位置”时,警车追上货车,所用时间
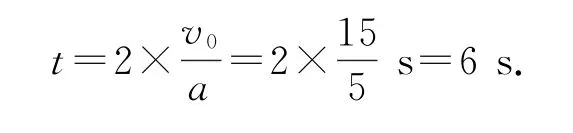
2 模型应用
例1第24届冬季奥林匹克运动会于2022年2月4日在北京开幕.越野滑雪是冬奥会的一个重要项目,若某次比赛中运动员甲以v1=10 m·s-1的速度向终点滑行,在他后方x0=32m 处的运动员乙的速度为v2=8m·s-1,此时乙将以加速度a2=1m·s-2开始冲刺.设乙开始冲刺时为0时刻,运动员的冲刺过程均可视为匀变速直线运动.
(1)乙追上甲前距离甲的最远距离为多少?
(2)4s末乙距甲的距离为多少?
解析以甲为参考系,乙相对甲具有向后的初速度

向前的加速度
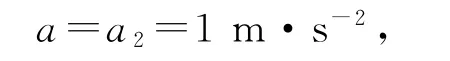
乙相对甲做“竖直上抛运动”.
(1)当乙运动到“竖直上抛运动的最高点”时,与甲相距最远,最远距离
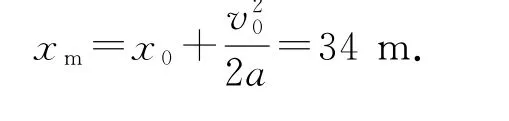
(2)t=4s时,由“竖直上抛运动”的规律可知,乙距甲的距离

例2如图3所示,离地面足够高处有一竖直空管,管长为l=0.2 m,M、N为空管的上、下两端,空管以恒定的速度v0向下做匀速直线运动,同时在空管下端距离d=0.25m 处有一小球开始做自由落体运动,g取10m·s-2.

图3
(1)若经过t0=0.2s,小球与N点等高,求空管的速度大小v01;
(2)为了使小球在空管内部运动的时间最长,求空管的速度v02的大小和这个最长时间.

图4
解析以空管为参考系,小球具有竖直向上的初速度v0和竖直向下的加速度g,可视为小球相对于空管做“竖直上抛运动”,其运动过程示意图如图4所示.
(1)小球与N点等高时,有
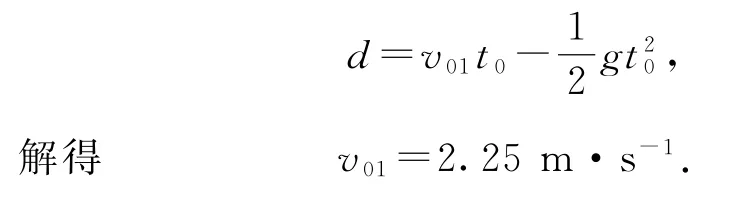
(2)当小球做“竖直上抛运动”的最高点与空管的M端等高时,小球在空管内部运动的时间最长.
小球与M点等高时,则有

故小球在空管内部运动的最长时间

点评本题涉及的是竖直方向的追及相遇问题,情境新颖,运动过程较为复杂.从常规思路进行分析求解,需要有较强的空间想象能力和一定的综合分析能力.这里通过改选参考系,构建小球的“竖直上抛运动”模型,将多物体的运动过程转化为单一物体的运动过程,从而在动与静的转化和结合中使问题得以顺利解决.
从本质上来讲,追及相遇问题归根结底是相对运动问题,因此,在很多情况下,认识运动的相对性,合理选择参考系,可使复杂的运动过程和问题情境变得简洁而清晰,从而在参考系的转化和运动模型的重新构建中,有效促进学生对物理规律的深度理解,丰富学生的解题思路,真正提高学生分析问题和解决问题的能力.而模型的构建、归类和应用作为物理学的重要内容,也必然是新高考中突出考查的重点和热点.
(完)

