荡秋千问题
俞 鹏
(清华大学附属中学)
多数人都有这样的经验:荡秋千时,无须借助外力,只需通过重心位置的变化,就可以让秋千越摆越高.这一现象背后的原因是什么呢? 为了研究其中的原因,首先对模型进行简化,做如下假设:1)忽略人的宽度,将人当作质量分布均匀的长条形(高度可变);2)人控制身体与秋千的摆线始终平行,且摆线始终不会弯折;3)人的高度可以任意变化(从0到最大身高h),但始终保证质量均匀分布;4)忽略绳子和秋千底板的质量,整个系统只考虑人的质量即可.
如图1 所示,以逆时针为转动的正方向,摆长记为L,人的质量为m,人的重心到转轴的距离记作r,在角度为θ时,人受到重力与绳子拉力FT的作用,将人相对转轴的转动惯量记作I,则该瞬间有

图1
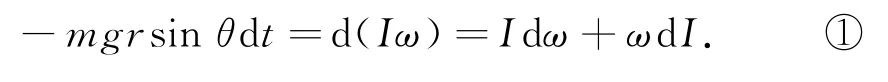
根据平行轴定理,可以写出
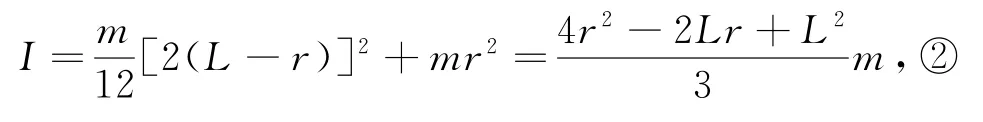
将式②对r求导可得
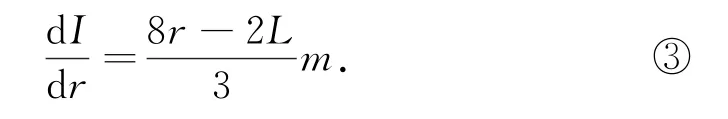
考虑实际情况,人身高不超过秋千绳长,即

将式④代入式③可知

式⑤说明,正常情况下,人站起会使得I变小,人蹲下则会使得I变大.
下面对式①做定性分析(取0<θ<).
若人的形态不变,即dI=0,则有dω<0,此时秋千正在减速上摆.为了方便后续讨论,不妨设人形态不变情况下,在dt时间内角速度变化为

若人发生形态变化,则在dt时间内角速度变化为

情况1ω>0,秋千正在逆时针上摆,此时式①左侧小于0.
若人的形态不变,即dI=0,则有dω=dω0<0,此时秋千正在减速上摆.
若人发生形态变化:如果dI>0(人正在下蹲),则dω1<dω0<0,即由于人的下蹲会使得秋千上摆时减速得更快,并且ω的绝对值越大,该影响越大;如果dI<0(人正在站起),则dω0<dω1<0,即由于人的站起会使得秋千上摆时减速得更慢,并且ω的绝对值越大,该影响越大.
情况2ω<0,秋千正在顺时针下摆,此时式①左侧小于0.
若人的形态不变,即dI=0,则有dω=dω0<0,此时秋千正在加速下摆.
若人发生形态变化:如果dI>0(人正在下蹲),则角速度变化dω1满足dω0<dω1<0,即由于人的下蹲会使得秋千下摆时加速得更慢,并且ω的绝对值越大,该影响越大;如果dI<0(人正在站起),则角速度变化dω1满足dω1<dω0<0,即由于人的站起会使得秋千下摆时加速得更快,并且ω的绝对值越大,该影响越大.
综上所述,站起过程有利于秋千越荡越高,而下蹲过程则会让秋千荡得更低.但荡秋千时我们必须不断交替地站起和蹲下,所以如何增加站起过程对秋千的影响同时削弱下蹲过程对秋千的影响就成了关键.
可见,任意时刻由人的形态变化产生的角速度变化都是随ω的绝对值的增大而增大的,所以如果能在角速度较大的地方(较低处)站起,且在角速度较小的地方(较高处)蹲下,就可以让秋千越荡越高.
为了帮助大家更好地理解,下面来讨论一种最理想的荡秋千方式:即让站起的动作全部发生在角速度最大的最低点,而让蹲下的动作全部发生在角速度最小的最高点.此时可以假设人每次的重心变化(蹲下或站起)都非常迅速,以至于每次蹲下或站起时秋千的位置都来不及变化,这样每次人在蹲下或站起时和对秋千的作用力以及身体各部分之间的作用力都远大于重力,也就是人和秋千之间、人身体各部分之间的内力矩都远大于重力矩,于是可以认为每次蹲下或站起的瞬间人相对转轴的角动量守恒.即

进一步将式⑦写成
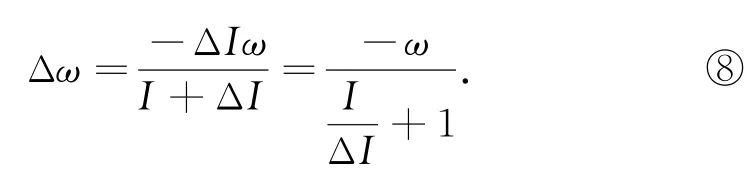
对式⑧进一步讨论.
情况1人突然蹲下,ΔI>0,则Δω与ω异号,即秋千会突然减速,为了将这种减速的效应降到最低,我们可以在ω=0的位置蹲下,即在最高点蹲下,此时Δω=0,不会因为下蹲而减速.
情况2人突然站起,ΔI<0,且因为转动惯量不会变为负数,所以一定有-ΔI<I,则+1<0,于是Δω与ω同号,即秋千会突然加速,为了将这种加速的效应发挥到最大,应选择ω最大的时刻站起,即在最低点站起,此时可以获得最大的Δω.
综上所述,将秋千荡高的最高效方式是:在最高点突然蹲下,在最低点突然站起.
有人提出过一个有趣的问题:秋千越荡越高的过程中,某次人在最低点突然站起,有没有可能使得秋千能在竖直面内做完整的圆周运动呢? 显然,为了让人能够完成这个高难度动作,就得让人在最低点突然站起后具有尽量大的机械能,这就要求突然站起前人的机械能也得尽量大,而在之前的摆动中绳子最多能到达水平状态(再高则绳会松弛),所以我们考虑最可能完成这个动作的方案:如图2所示,假设之前一次秋千摆角刚好到达90°,且人蜷缩成一团(质量全部集中在距离轴心L处的秋千底板),即图中A状态.然后人自然下摆到最低点B,并获得动能Ek0=mgL,接下来人突然站起,使得重心到轴的距离变为r,并假设之后人可以运动到最高点.人站起前相对轴的转动惯量I0=mL2,人站起后相对转轴的转动惯量已经由式②得出,即
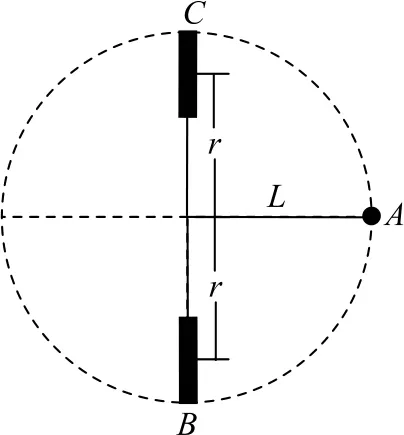
图2
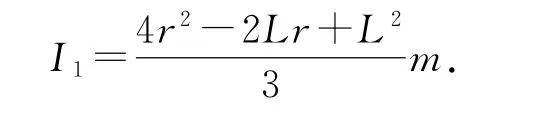
设在B点突然站起后的转动动能变为Ek1,由于站起瞬间角动量守恒,所以有
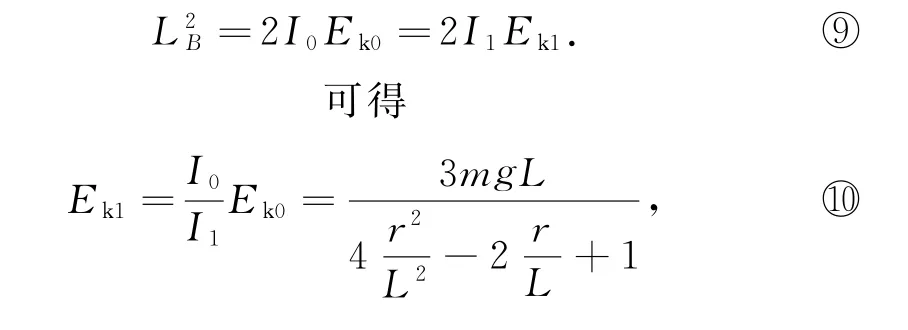
不妨令r=Lx,则式○10变形为
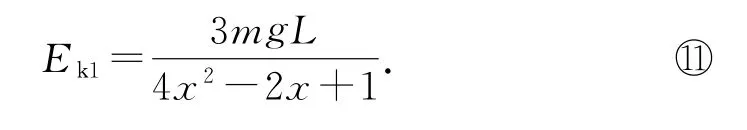
设到最高点C的转动动能为Ek2,并设C点处人的质心速度为vC2,则根据机械能守恒定律得

若要人能够通过最高点C,则需要
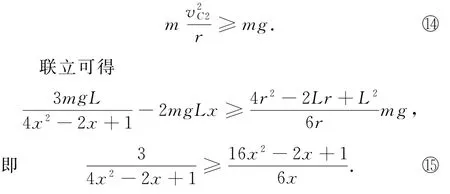
根据式④的假设可知0.5≤x≤1.所以可以保证式两边的分子和分母都大于0,于是式可化为
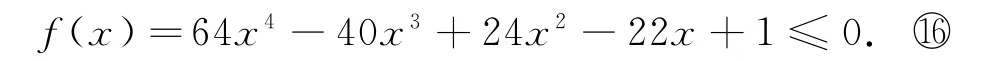
画出y=f(x)的函数图像,如图3所示.

图3
由图像可知f(x)<0的解为

也就是说,要想完成在最低点突然站起使得秋千能够做完整圆周运动的动作,人的身高h需要满足条件为
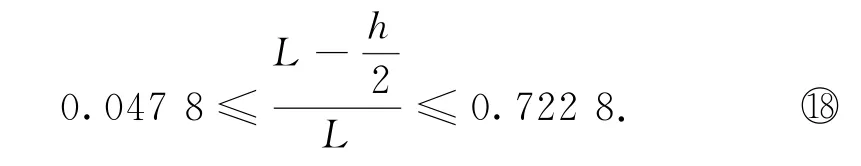
上式给出了要完成这个高难度动作对人的身高的限制条件,h的下限0.5544L比较好理解,而h的上限实际上是对应了人站起来比秋千还高的情况.如果要考虑式④的限制,则须写成0.5544L≤h≤L.
(完)

