三维弹性力学改进的插值型维数分裂无单元Galerkin方法权函数研究

孟智娟，房亚楠，迟晓菲

(太原科技大学应用科学学院，山西 太原 030024)

1 引言

弹性力学问题是典型的一种工程问题.目前求解弹性力学问题的数值方法包含有限元法[1]、有限差分法[2]、边界元法[3]和无网格法[4].无网格法对单元或网格无依赖性.三维弹性力学改进的插值型维数分裂无单元Galerkin法(IIDSEFG)是利用维数分裂法(dimension splitting method，简称DSM)将三维弹性体转化为一系列相关的二维弹性体，然后采用改进的插值型无单元Galerkin法(improved interpolating element-free Galerkin，简称IIEFG)对二维问题进行数值模拟，在分裂方向上采用FDM.最后得到了三维弹性问题的离散系统方程.

IIEFG方法为带有非奇异权函数的插值型移动最小二乘法(improved interpolating moving leastsquares，简称IIMLS)近似构造试函数.其中，基函数选择具有插值特性的正交函数族，权函数选为非奇异函数，在形函数的构造过程中，权函数起到重要的作用.以此，研究权函数的选择对数值结果的影响具有重要意义.常见的权函数一般有三次样条、四次样条、指数函数和正定紧支径向基函数.张赞等使用改进的无单元Galerkin方法(improved element-free Galerkin，简称IEFG)模拟三维问题时，采用了四次样条函数作为权函数[5].Lancaster和任红萍等建立二维移动最小二乘插值法时，均采用奇异权函数构造满足插值特性的形函数[6].王聚丰等提出了基于非奇异权函数改进的移动最小二乘插值法，并建立了IIEFG方法[7].苗雨等建立三维弹性力学的奇异混合边界节点法无网格分析[8].但是上述无网格方法在求解三维问题时计算效率普遍偏低.DSM方法与无网格方法的耦合能提高IIEFG方法的计算效率.李开泰等首先选用DSM求解三维方程[9].候延仁等应用DSM求解了一个三维椭圆方程[10].Ter Maten EJW应用DSM求解四阶抛物型偏微分方程[11].Bragin等应用DSM来分析守恒定律[12].本文作者提出维数分裂无单元Galerkin方法[13-14]和IIDSEFG方法来模拟三维问题[15].程珩应用改进的复变量无单元Galerkin方法模拟三维问题[16].吴谦等提出DSM与奇异权函数无单元Galerkin插值法相结合解决三维问题[17].

IIDSEFG方法在构造形函数时权函数起到至关重要的作用，本文通过选择不同权函数构造的可直接施加本质边界条件的IIDSEFG方法与采用罚函数法施加本质边界条件的IEFG方法进行比较，说明IIDSEFG解决三维弹性力学问题的有效性及权函数研究的重要性.

2 三维弹性力学问题弱格式模型的建立

三维弹性力学问题的平衡方程为

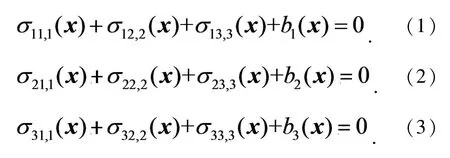
其中σij(i，j＝1，2，3)是应力分量，bi(i＝1，2，3)是单位体积上的体力分量.

对应的边界条件为

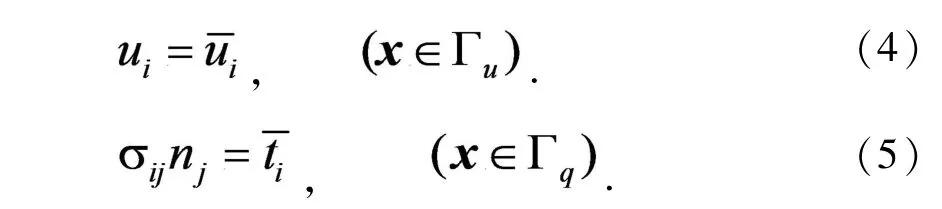
其中ui为位移分量，Ω为带有边界的三维求解域，且为位移边界Γu上的已知位移分量，为应力边界Γq上的已知面力分量，nj为边界上的单位外法向向量的分量.

采用IIDSEFG方法求解，选取x3作为分裂方向，问题域在x3方向上平均分裂为L层，即形成L＋1个二维子域Ω(k)，，相邻两层之间的距离为Δx3于是有

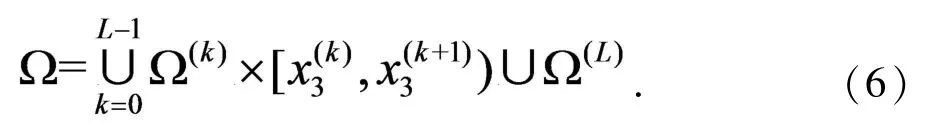
其中

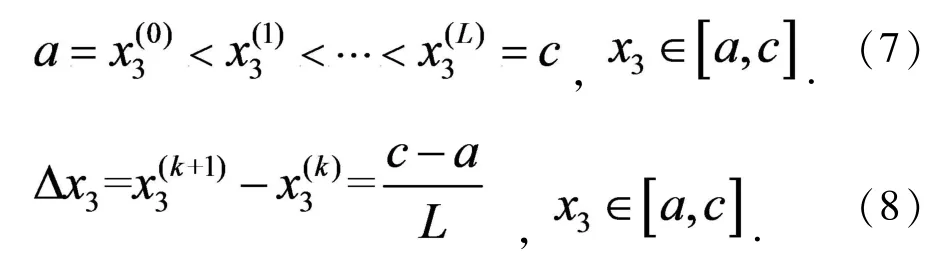
固定，三维弹性力学问题转化为二维弹性力学问题，直角坐标系下平衡方程(1)、(2)和边界条件(4)、(5)转化为

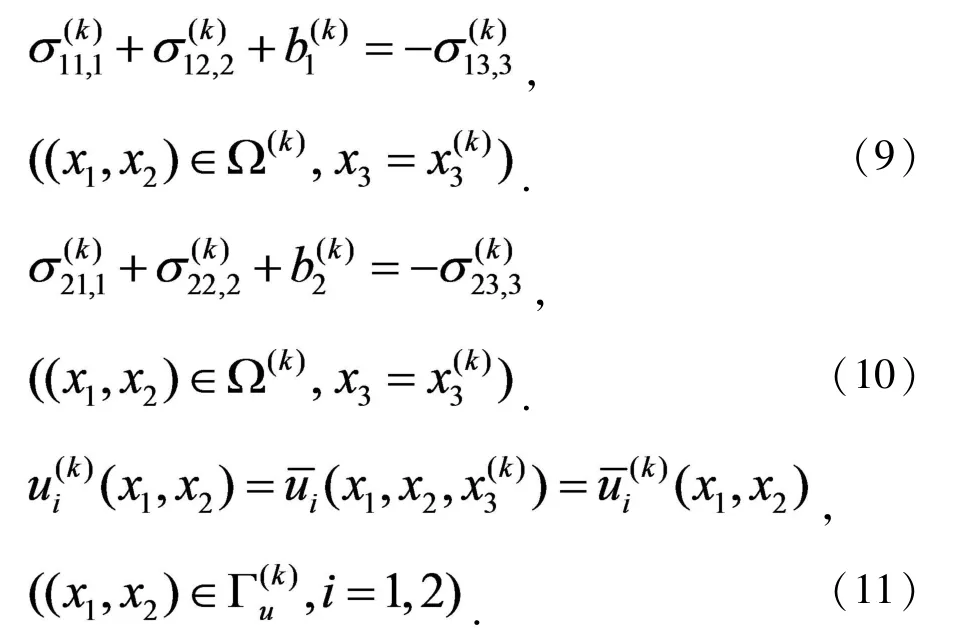
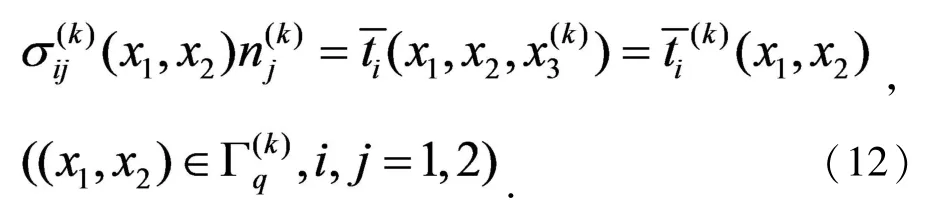
选用基于非奇异权函数的IIEFG方法求解二维边值问题(9)-(12).由于形函数采用IIMLS方法构造，所以具有插值特性，可直接施加本质边界条件，本文选用对角元素化为1的方法直接处理.得到式(9)-(12)的Galerkin积分弱形式为

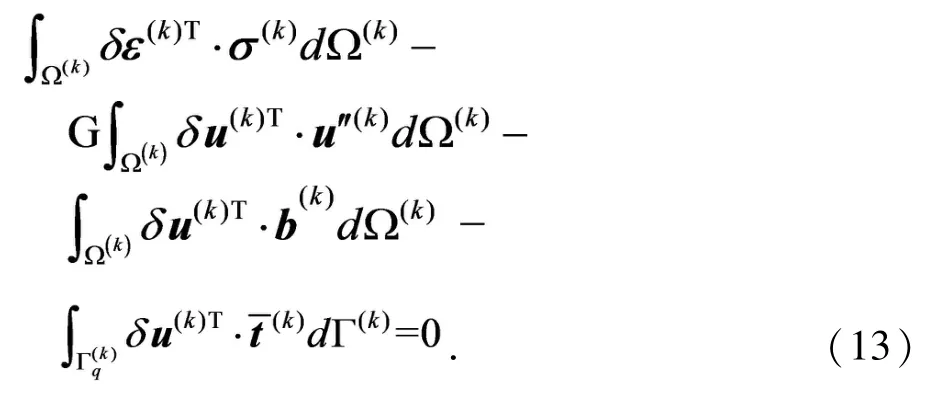
其中

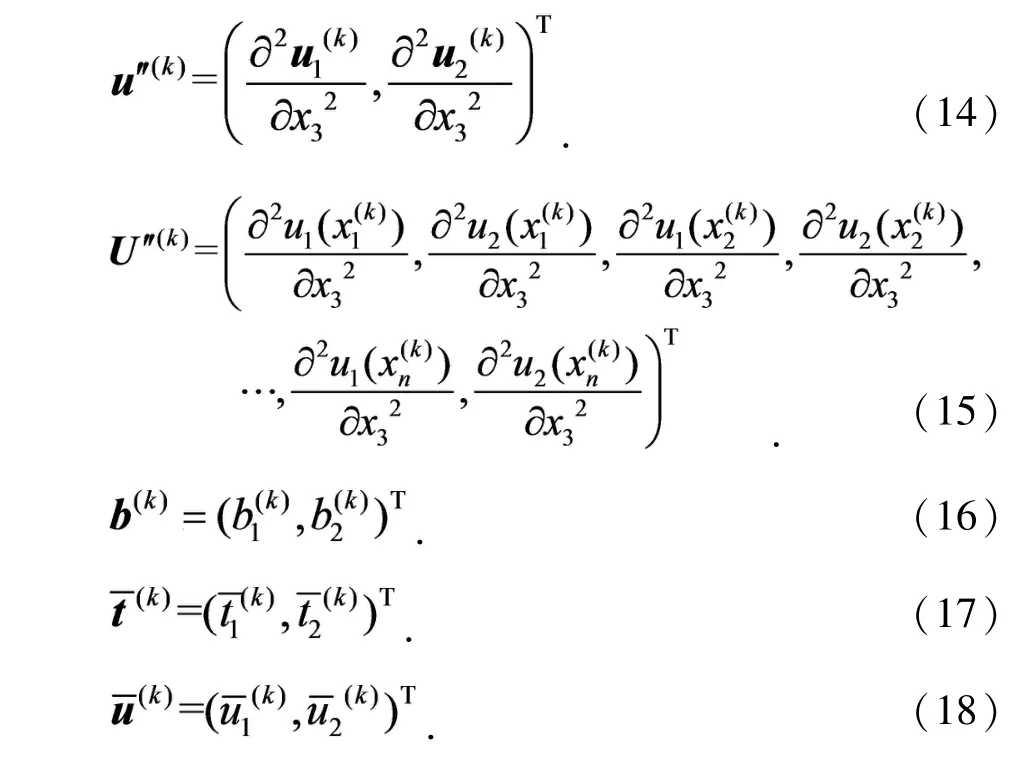
3 三维弹性力学问题的IIDSEFG方法及其权函数研究

3.1 IIMLS方法

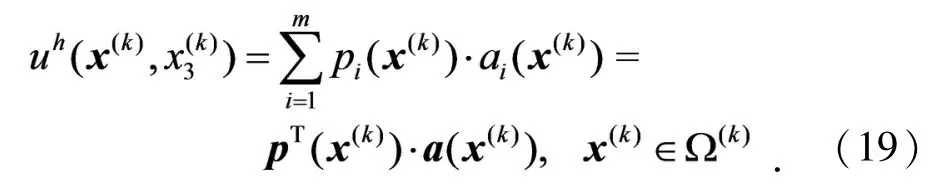
其中pi(x(k))为基函数，m为基函数的个数，ai(x(k))为基函数的系数.

为了构造所需的基函数，首先，选择线性基函数如下

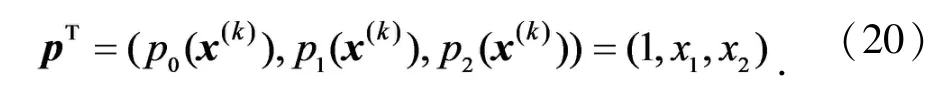
然后，对基函数做变换

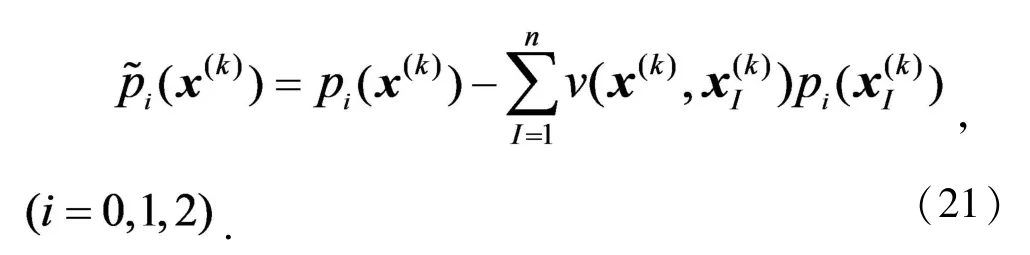
其中

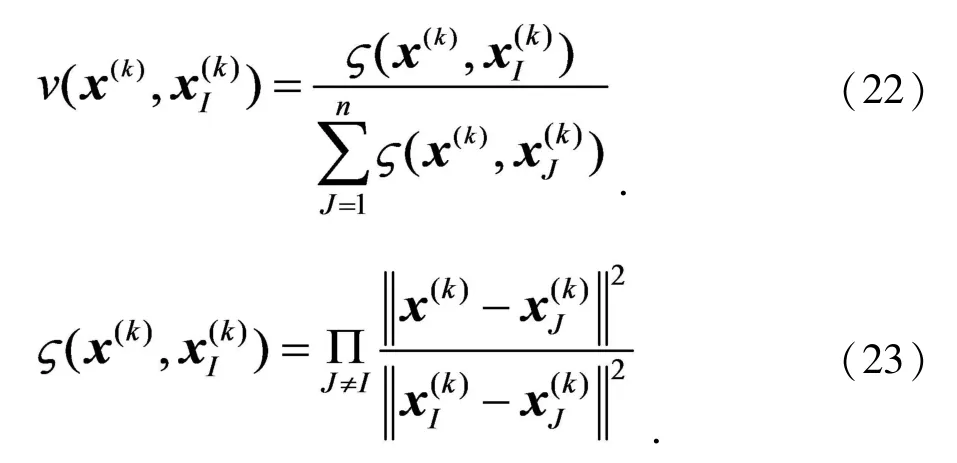
对x(k)点处的位移u(x(k))作类似的变换，得到

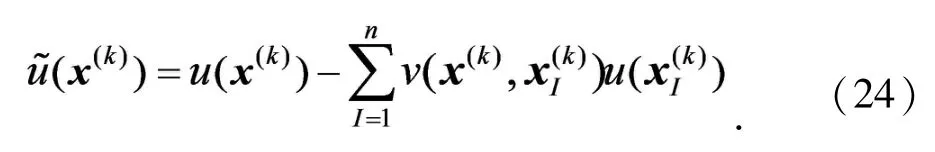
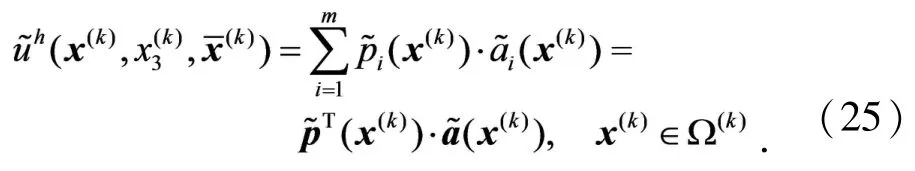
定义泛函

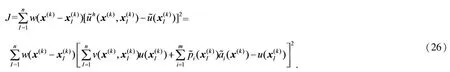
其中，w(x(k)-x1(k))为权函数，x1(k)，I＝1，2，…，n为网格节点x(k)的影响域内覆盖的节点.

令

得

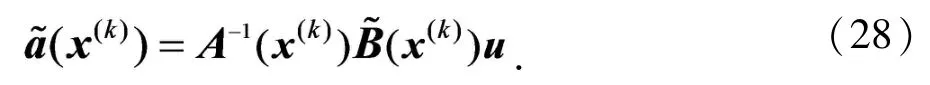
其中

从而有

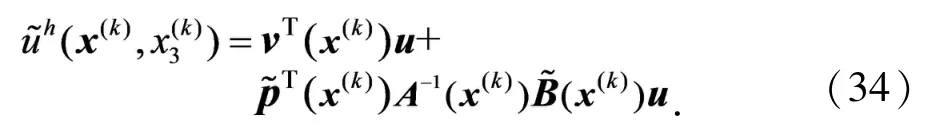
其中

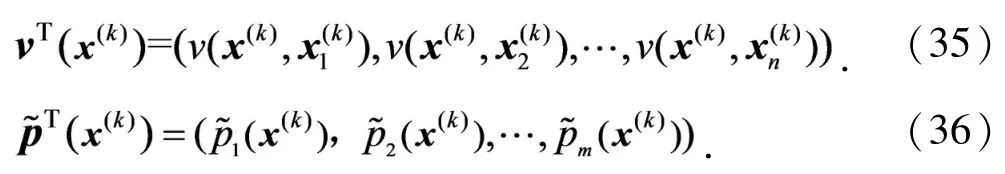
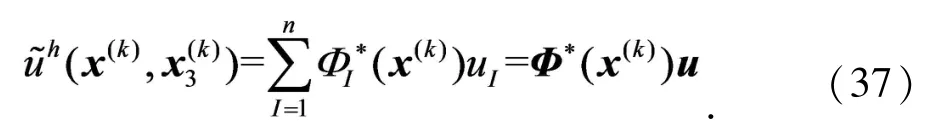
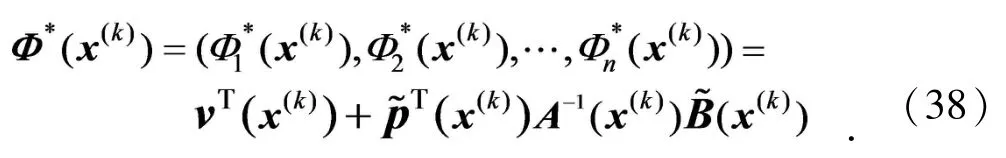
3.2 IIDSEFG方法权函数研究

权函数是具有紧支特性的局部函数，其影响域常为圆形域和矩形域.一般满足如下性质:

1)正定性，设Ω1为节点x1处权函数的影响域，ρ1表示x1的影响域大小.在Ω1内，w(x-x1，ρ1)＞0；

2)紧支性，在影响域Ω1外，w(x-x1，ρ1)＝0；

4)单调递减性，w(x-x1，ρ1)是的单调减函数；

5)插值性，当ρ1→0时，这里δ(x)为Diracδ函数.

函数本身的连续性和可导性是衡量权函数的标准.常见的权函数有三次样条函数，四次样条函数，指数函数和正定紧支径向基函数.其示意图如图1所示，具体表达式分别如下

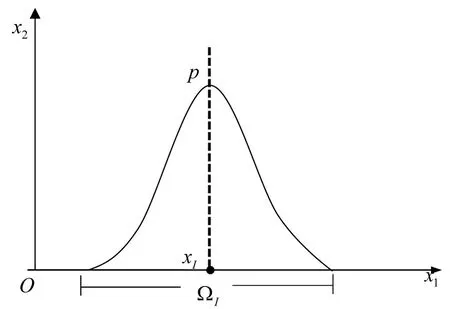
图1 权函数的示意图Fig.1 Schematic diagram of weight function

1)三次样条权函数为

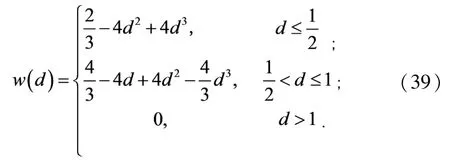
2)四次样条权函数

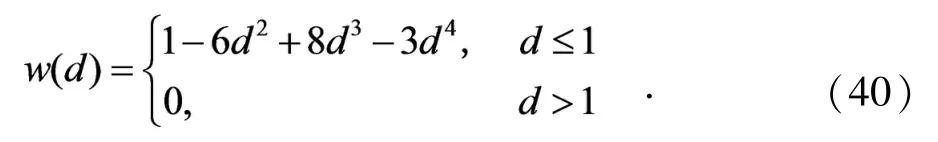
3)指数函数

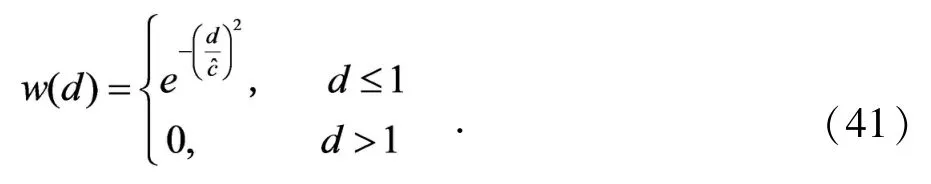
4)正定紧支径向基函数

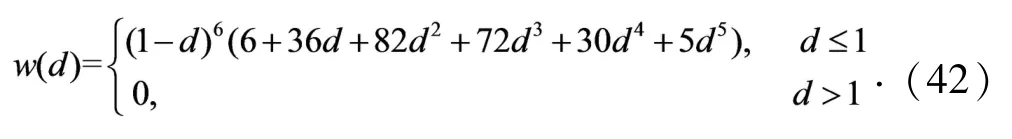
3.3 三维弹性力学问题的IIDSEFG方法

基于非奇异权函数的IIEFG方法构造二维弹性子问题的近似函数，等式(37)可以表示为

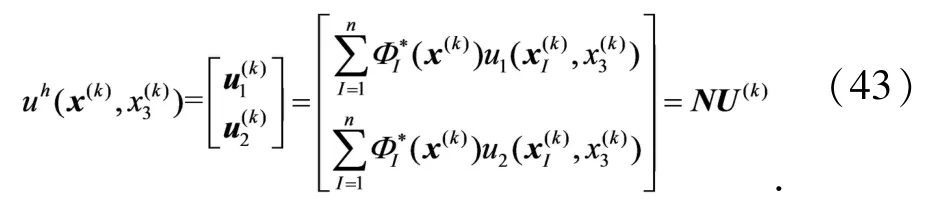
其中

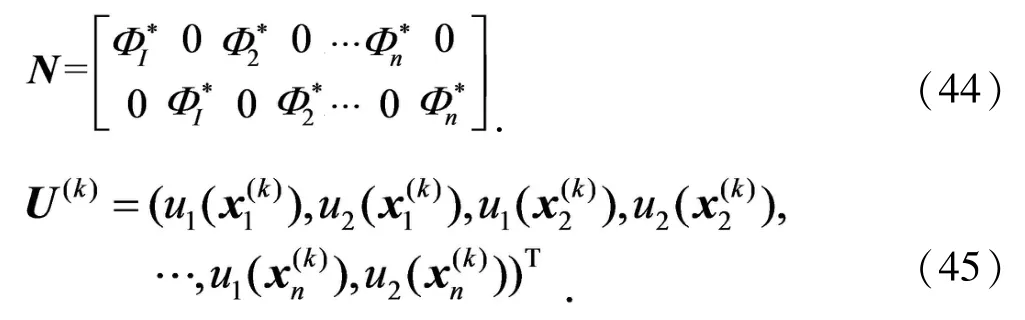
二维子域Ω(k)中，任意点的应变为

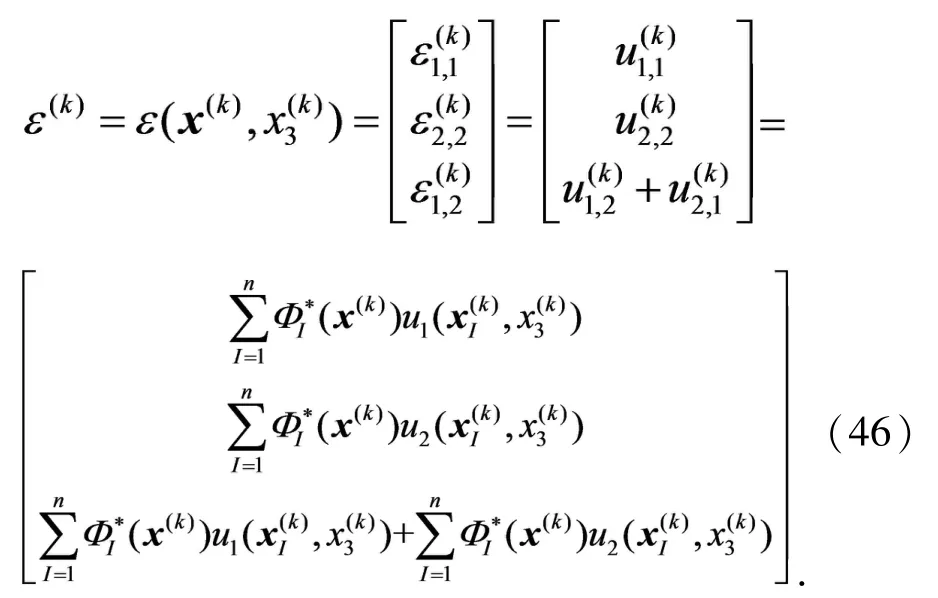
可以表示为

古典詩词文化是我国文学艺术宝库中的一朵艳丽的奇葩，因其本身具有的语言凝练、意境深远、短小精悍、言简意赅和朗朗上口的特点多受到幼儿的喜爱。并且从传承和发扬我国优秀传统文化的角度来说，开展古典诗词教学培养幼儿良好阅读习惯，正是顺应了这一教学要求的表现。幼儿在这一教学阶段具有很强的可塑性，所以幼儿教师应当紧紧抓住这一有利契机，让幼儿爱上诗词，爱上阅读，从小强化幼儿的文学素养。

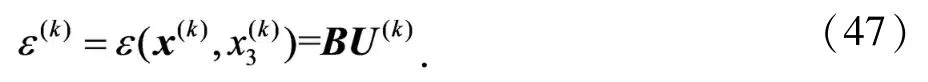
其中

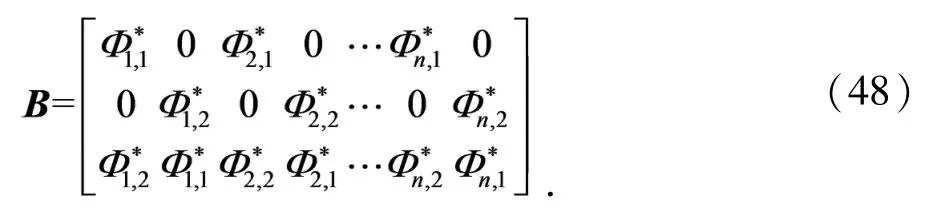
二维子域Ω(k)中，任意点处的应力为

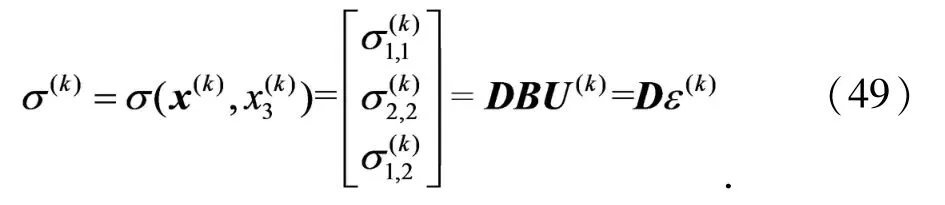
这里的D为弹性矩阵，且

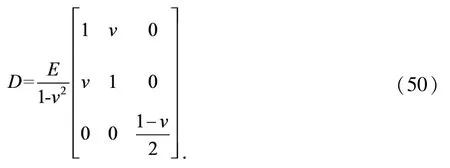
E为弹性模量，v为泊松比.

由式(43)可得到

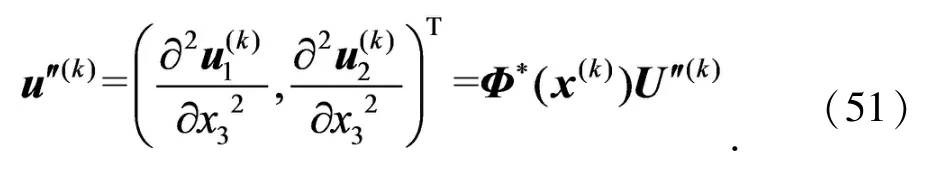
将式(43)、(47)、(49)、(51)代入式(13)中，得到

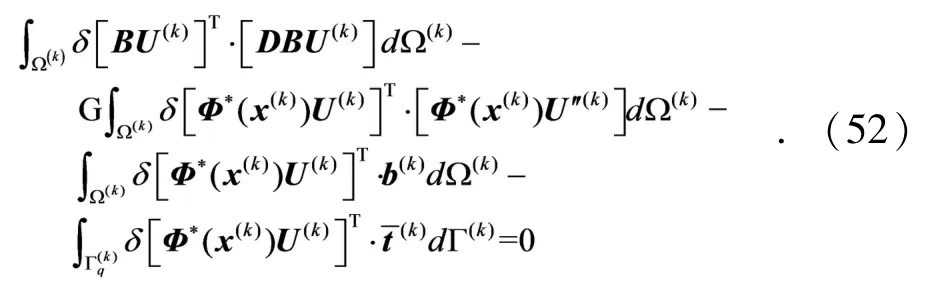
讨论式(52)中的每个积分，可以得到最终的离散方程.

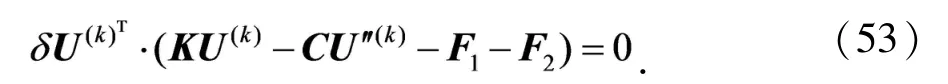
接下来，求解方程(54)，在分裂方向x3的区域[a，c]上均匀地插入L-1个点，在分裂方向上采用FDM，即

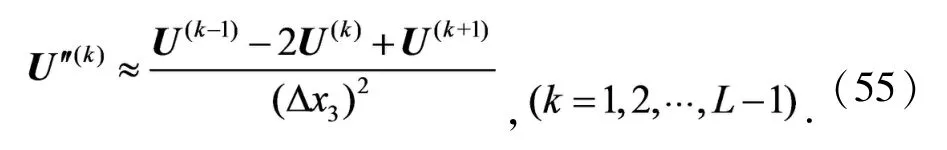
从而，方程(54)可以表示为

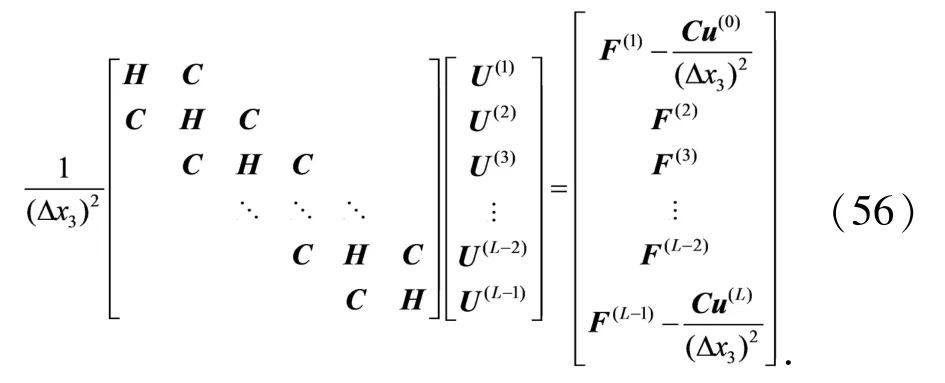
这里

方程(56)的解为中间层x3＝x3(1)，x3(2)，x3(3)，…上各节点位移在x1和x2方向上的数值解.同样利用IIDSEFG方法可以求解由方程(2)和(3)及其对应的边界条件构成的边值问题，得到节点处位移在x2和x3方向上的数值解.

4 数值算例

4.1 受均匀分布载荷的立方体

如图2考虑受均匀分布载荷的立方体，立方体的边长为2 m，分布载荷为σ＝32 MPa，泊松比为v＝0.25，剪切模量为G＝15 000 MPa.对应位移的解析解为

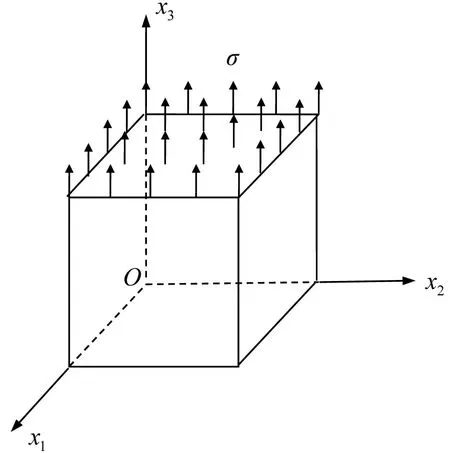
图2 受均匀分布载荷的立方体Fig.2 A cube subjected to uniformly distributed loads

表1显示了控制节点影响域大小的比例参数dmax＝1.05，网格节点分布为11×11×11时，IIDSEFG方法和IEFG方法在不同权函数下相对误差和CPU时间.可见用IIDSEFG方法求解该问题时，权函数选择四次样条函数，整体相对误差最小为3.318×10-16，CPU运行时间最少为0.91 s.用IEFG方法求解该问题时，权函数选择四次样条函数结果最好，整体相对误差为2.529 8×10-11，CPU运行时间为17.94 s.同时可见，IIDSEFG方法比IEFG方法具有更好的计算精度与计算效率.

表1 IIDSEFG和IEFG选取不同权函数的相对误差与CPU运行时间Table 1 Relative error norm and CPU times of different weights of IIDSEFG and IEFG

图3为选取三次样条函数作为权函数，IIDSEFG方法在平面x2＝1.0时的三维数值结果.

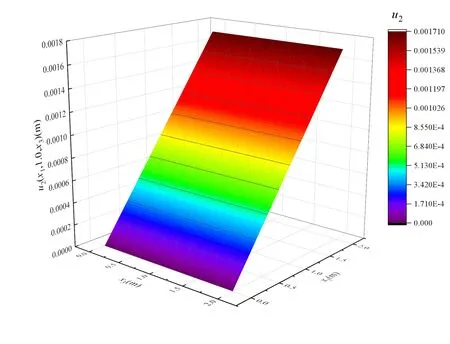
图3 IIDSEFG方法在平面x2＝1上位移数值解Fig.3 Numerical solution of IIDSEFG method's displacement on the plan x2＝1

4.2 受自重的等截面杆

图4所示的等截面杆的单位体积重力为ρg，体力为b1＝b2＝0，b3＝-ρg.应力为σ33＝ρgx3，σ11＝σ22＝σ12＝σ23＝σ13＝0.相关几何和材料参数为l＝36mm，泊松比 为v＝0.15，杨氏模量为E＝2.069×104MPa，密度为ρ＝2 405 kg/m3.位移场的解析解

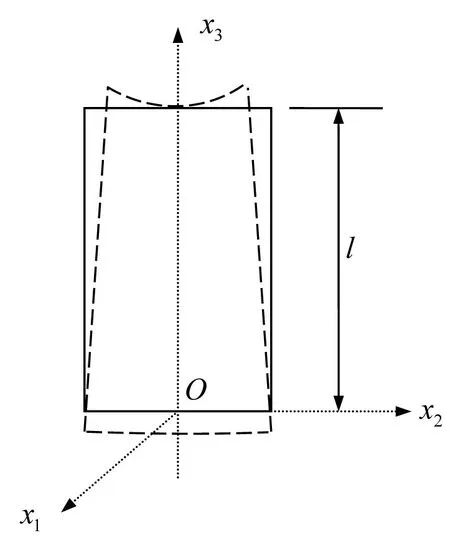
图4 受自重的等截面杆Fig.4 A constant section bar subjected to dead weight

表2和表3分别显示了在dmax＝1.10，网格节点分布均为5×5×11时，IIDSEFG方法和IEFG方法在不同权函数下位移u3和应力σ33沿方向x3的整体相对误差和CPU运行时间.可见采用IIDSEFG方法求解位移u3时，权函数选择四次样条函数结果最好，相对误差为7.23×10-4，CPU运行时间为0.63 s.求解应力σ33时，权函数选择三次样条函数结果最好，相对误差为5.24×10-3.用IEFG方法求解位移u3时，权函数选择三次样条函数结果最好，相对误差为6.43×10-4.求解应力σ33时，权函数选择正定紧支径向基函数结果最好，相对误差为3.78×10-2.同时可见，IIDSEFG方法比IEFG方法具有更好的计算效率.

表2 IIDSEFG与IEFG方法选取不同权函数u3整体相对误差和CPU运行时间Table 2 Overall relative errors and CPU times of the IIDSEFG and IEFG methods with different weights function u3

表3 IIDSEFG与IEFG方法选取不同权函数σ33整体相对误差和CPU运行时间Table 3 Overall relative errors and CPU times of the IIDSEFG and IEFG methods with different weights function σ33

图5为选择三次样条函数作为权函数，采用IIDSEFG方法在平面x2＝1上位移u2(x1，1.0，x3)的三维数值计算结果.

5 结论

IIDSEFG方法将三维弹性力学问题沿着分裂方向划分为一系列相关的二维弹性力学问题.用IIEFG方法求解二维弹性力学问题，在分裂方向上采用FDM.选用基于非奇异权函数的IIMLS方法构造满足插值特性的形函数，用对角元素化为一的方法直接处理本质边界条件，最终得到离散的方程.本文研究选取不同权函数对三维弹性力学IIDSEFG方法数值计算结果的影响.通过分析典型数值算例，用IIDSEFG方法的数值解与IEFG方法的数值解和解析解进行对比，说明了采用IIDSEFG方法解决三维弹性力学问题的有效性及权函数研究的重要性.