一种基于α-β-γ滤波的距离方位跟踪滤波算法

何永青，彭良福，林云松，权 雨

(1.西南民族大学电气信息工程学院，四川 成都 610041；2.四川省气象服务中心，四川 成都 610072；3.电子科技大学自动化工程学院，四川 成都 611731)

在机载防撞系统(Traffic alert and Collision Avoid-ance System，TCAS)的防撞逻辑中，需要对目标飞机进行监视和跟踪[1].而对目标飞机监视和跟踪的主要观测量是本机与目标飞机之间的相对距离和方位角(本机机头的正前方与目标飞机之间的夹角).通过对目标飞机的相对距离和方位角的观测值进行处理，形成目标飞机的航迹信息，从而实现对目标飞机的跟踪[2-3].由于观测到的本机与目标飞机之间的相对距离和方位角可能存在误差，因此在工程上需要对相对距离和方位角的观测值进行滤波，常用的滤波器是卡尔曼滤波[4-5].由于卡尔曼滤波器中增益矩阵的计算量比较大，为了减少增益矩阵的计算量，对于匀加速运动(CA)模型，一般采用α-β-γ滤波[6-7].为了改善滤波效果，减小滤波误差，本文给出了一种基于α-βγ滤波的距离方位跟踪滤波算法.该算法适用于机载防撞系统中对匀加速运动目标的距离方位进行跟踪.

对于量测在极坐标系下的滤波系统来说，构造滤波方程时，既可以将状态向量取为直角坐标向量，也可以取为极坐标向量.前者将面对量测方程的非线性问题，后者将面对状态方程的非线性问题.两种方法进行扩展卡尔曼滤波后的估计精度几乎相同[8-9].在直角坐标系中，测量误差之间是相互耦合的.如果在x、y方向采用解耦滤波器代替耦合滤波器将会导致跟踪精度的降低.但是在工程实际应用中，经常将直角坐标系解耦，其所产生的误差可以忽略不计[10-11].因此，本文给出的距离方位跟踪滤波算法采用直角坐标系，先把极坐标系下的测量值转换到直角坐标系中，直接将相对距离和方位角分别在x、y方向进行投影，再利用卡尔曼滤波对坐标转换后的数据进行滤波处理.

1 α-β-γ滤波算法

α-β-γ滤波器是针对目标匀加速运动模型(CA，Constant Acceleration)的卡尔曼滤波器的稳态解形式.在一般情况下作以下假设:目标匀加速运动和平稳观测噪声.描述目标运动的状态X是三维向量，即，其中x，和分别为运动目标的位置向量、速度向量和加速度向量，则目标的状态方程为[12-13]:

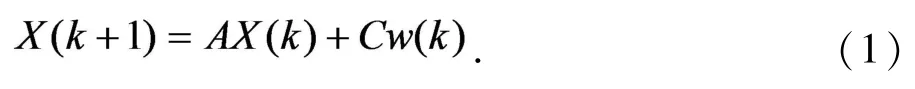
式中:X(k＋1)代表第k＋1时刻α-β-γ滤波器对系统状态X(k)的估计值；状态转移矩阵是，输入关系矩阵，过程噪声w(k)是均值为零，方差为Q＝E[w(k)w(k)T]的高斯白噪声.

观测方程的表达式为:

式中:y(k)代表系统第k时刻的位置观测量；测量矩阵D＝[1 0 0]；测量噪声v(k)为均值为零，方差的高斯白噪声.滤波方程为[14]:

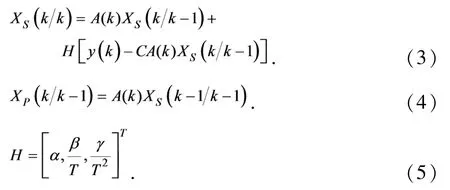
其中，H为增益矩阵，为k时刻的平滑向量，为对k时刻的预测向量.

由于Q、O的选取会影响滤波器的精度，而α、β、γ与Q、O直接相关，所以α、β、γ的选择必须考虑Q、O，即噪声特性与动态性能，同时根据多种的优化规则，工程实践中常用下式作为α、β、γ的参数[15].

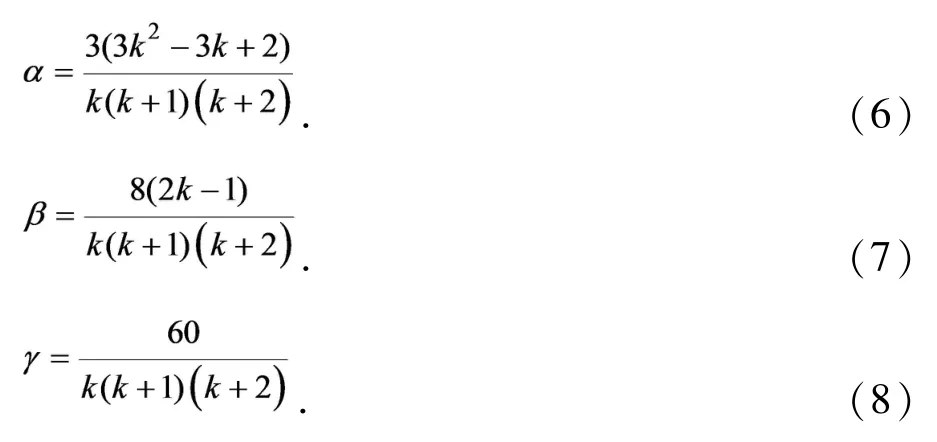
2 距离方位跟踪滤波算法

距离方位跟踪滤波算法是在α-β-γ滤波的基础上，在直角坐标系中，根据方位角将相对距离R投影在x、y方向上，再分别对x、y方向进行滤波，从而实现对运动目标的跟踪.

在TCAS中，两架飞机之间最接近点的距离是两机到达最接近点(CPA，Closest Point of Approach)时的相对斜距.如图1所示，两架飞机之间的相对距离R位于连接两架飞机的一个斜面上.根据两机之间的方位角可以把两机之间的相对距离在这个斜面上的x、y方向进行投影，这样就把三维空间飞机的防撞问题变成了二维斜面上飞机的防撞问题[16].在这个斜面上建立的以本机为原点的直角坐标系如图2所示.

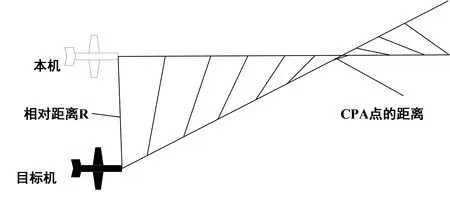
图1 两点间最接近点(CPA)的距离Fig.1 The closest distance between two points(CPA)

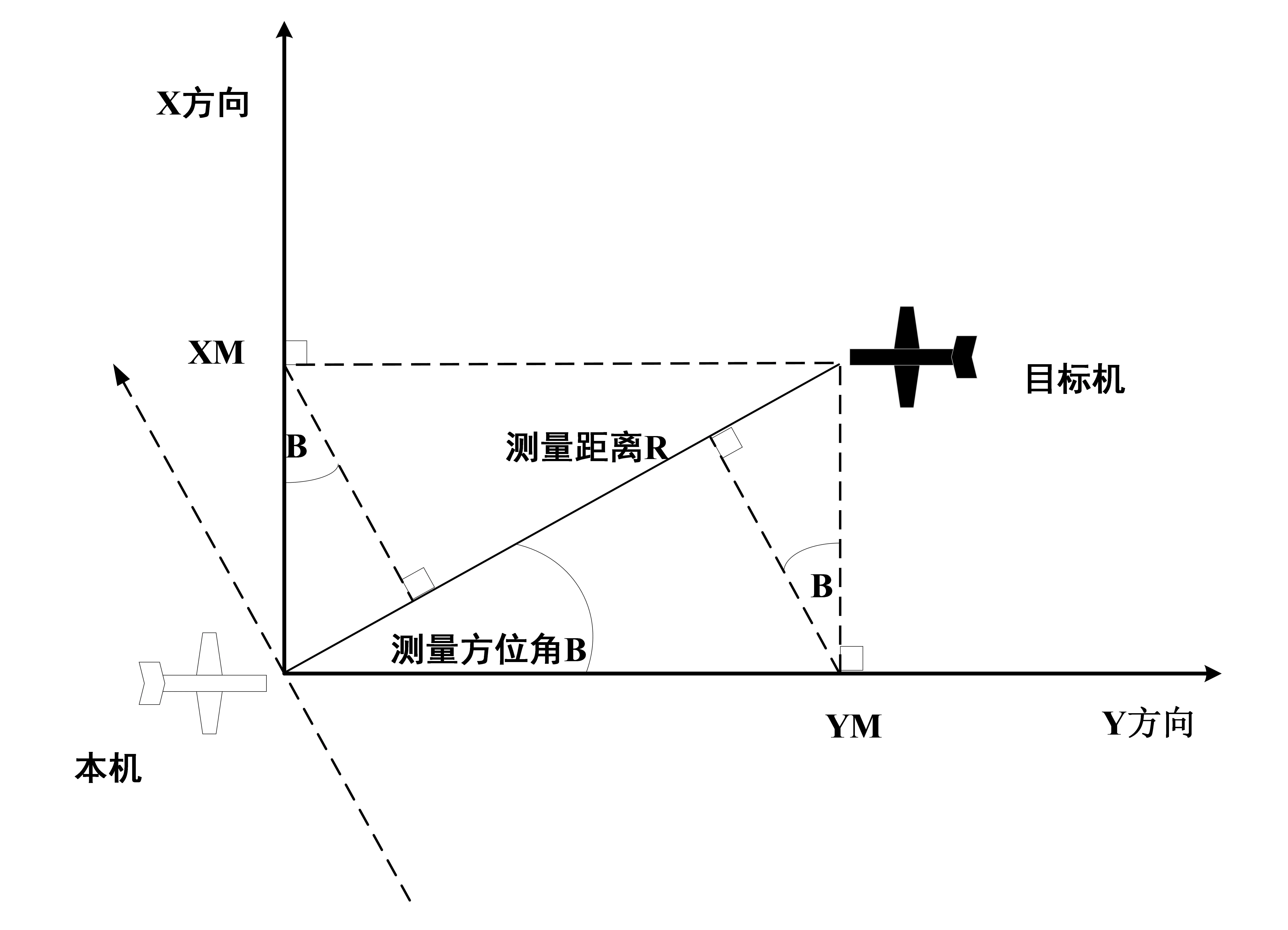
图2 目标跟踪距离方位投影示意图Fig.2 Projection diagram of distance azimuth target tracking

在图2中，将本机作为观测点，目标飞机作为目标，R为观测点与目标之间的相对距离，B为观测方位角，根据目标运动的回波数据(目标与观测点之间的相对距离R和方位角度B)判断目标做匀加速运动来建立系统模型.

首先，通过系统模型对k时刻目标进行预测，进行坐标变换，将目标的位置投影到直角坐标系中的x、y方向上.k时刻预测的距离为

其中，Xk和Yk分别代表投影到x和y方向的k时刻的测量距离，且将(9)式化解得:

将上式求导，可得笛卡尔坐标系下的误差为:

公式(12)、(13)表明，x、y方向的误差包括距离方向的误差和距离正交方向的误差两部分.

在k-1时刻，通过系统模型对k时刻目标进行预测.x、y方向的一步预测值:

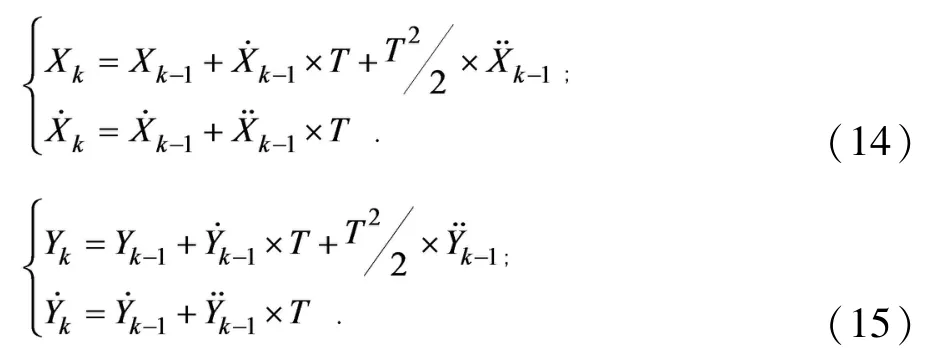
所得到的状态方程为:

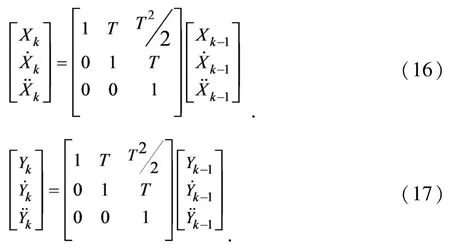
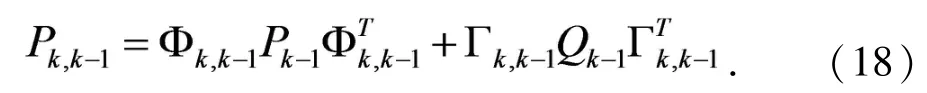
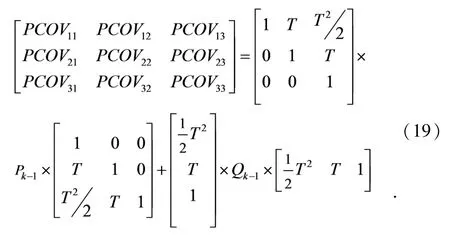
预测协方差矩阵与α/β/γ的关系[17]，及与距离正交方向位置、速度的平滑参数(W1/W2/W3)的关系如下，式中VAR＝R2×7.569×10-3是距离正交方向的测量方差.

计算x、y方向的距离方向的残差，以及距离正交方向的残差，如下:

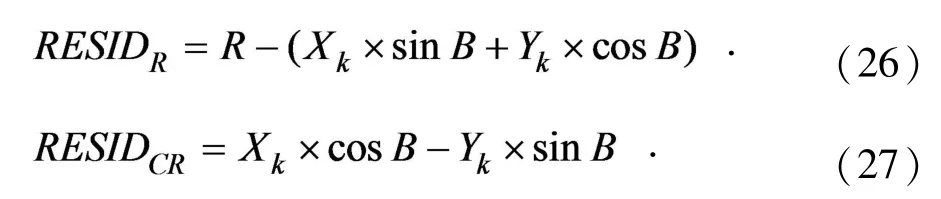
将距离方向的残差RESIDR以及距离正交方向的残差RESIDCR投影到x、y方向，得状态估计值:

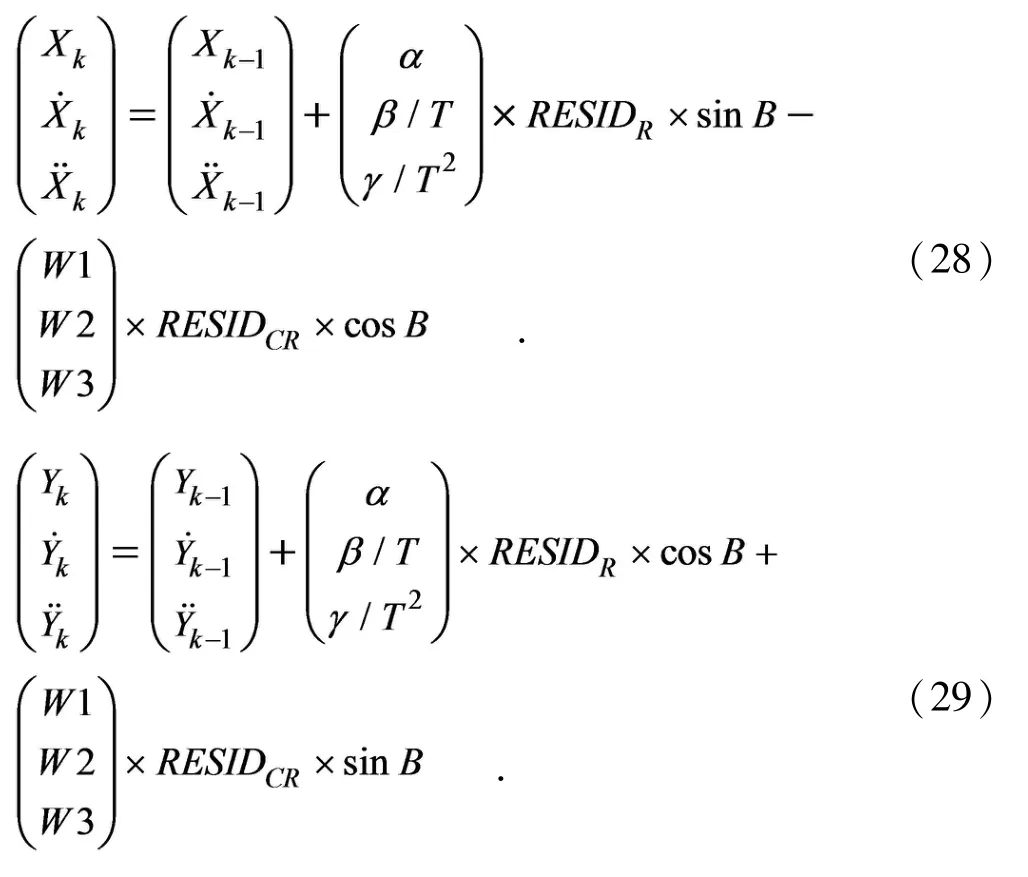
x、y方向滤波器是卡尔曼滤波器，将相对距离R和方位角度B投影到x、y方向后，采用卡尔曼滤波器进行滤波.滤波后将x、y方向的数据重新合成距离和方位角度，从而完成了距离和方位角度的滤波.

3 仿真结果及分析

为了验证距离方位跟踪滤波算法的性能，将其与传统的α-β-γ滤波算法进行比较，并对这两种滤波算法进行200次蒙特卡罗仿真[18].计算机仿真的参数选取如下:

假设两架飞机在同向飞行，目标飞机在做匀加速运动，初始速度Vb0＝700 km/h，加速度a＝0.8m/s2，本机做匀速运动，初始速度Va0＝900 km/h，目标飞机相对于本机的初始方位角B＝30°，观测周期T＝1s，仿真时间t＝500 s，两机之间的相对距离R＝280 km，过程噪声的方差Q＝2.56，相对距离的测量方差Navr_r＝10 m，相对方位角的测量方差Navr_az＝2°.

计算机仿真采用MATLAB编程，仿真结果如图3至图8所示.其中，图3是相对距离的真实值与观测值的比较；图4是相对距离的观测误差；图5是相对方位的观测误差.图6是相对距离的真实值与经过αβ-γ滤波后的估计值比较；图7是相对距离的真实值与经过距离方位跟踪滤波后的估计值比较；图8是αβ-γ滤波与距离方位跟踪滤波估计误差的比较.

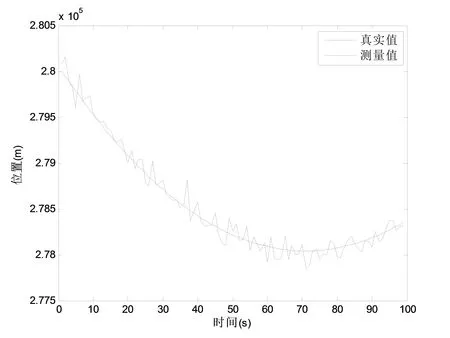
图3 相对距离的真实值与观测值的比较Fig.3 Comparison of the true value and the observed value for relative distance

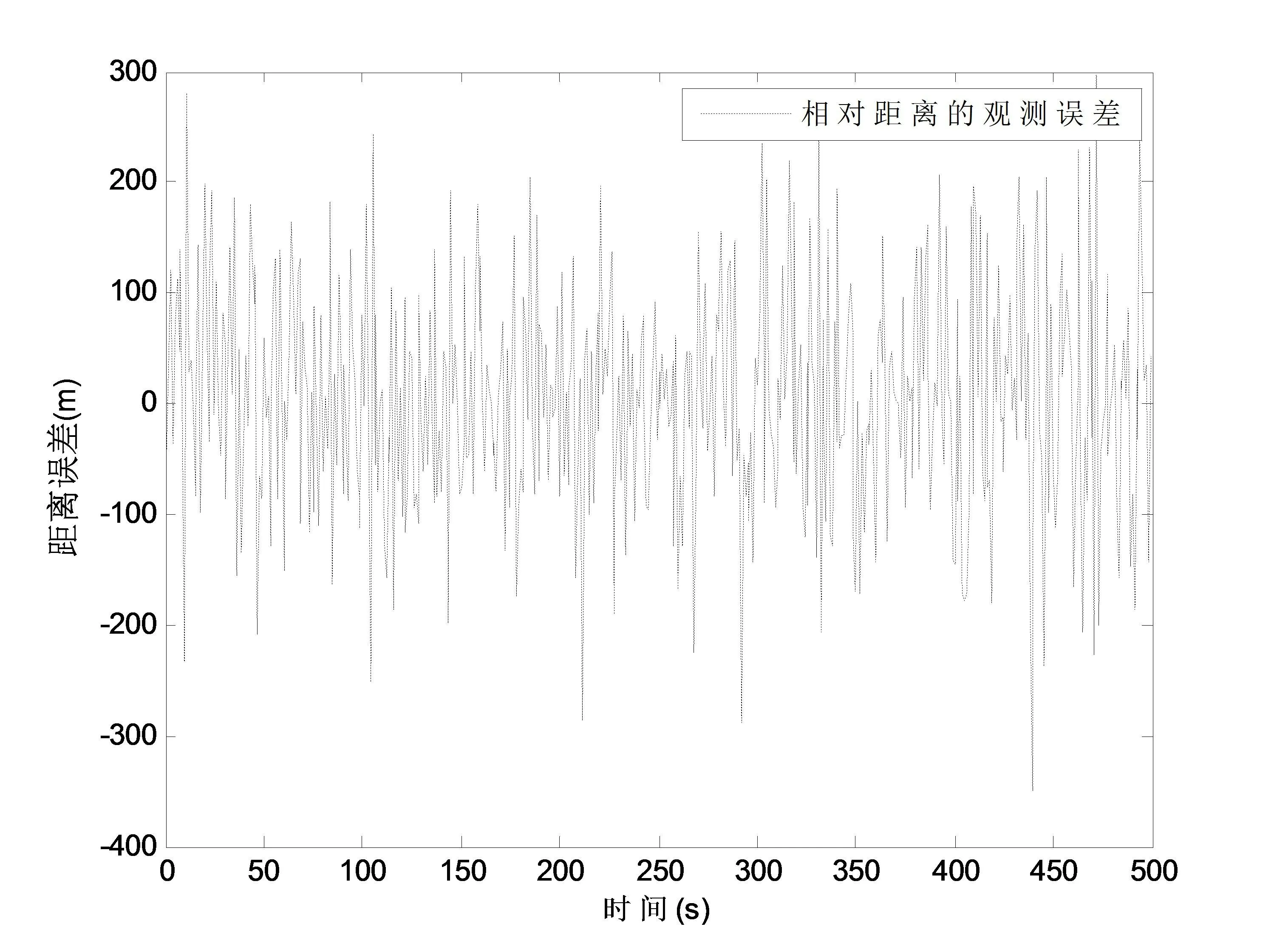
图4 相对距离的观测误差Fig.4 The observation error of relative distance

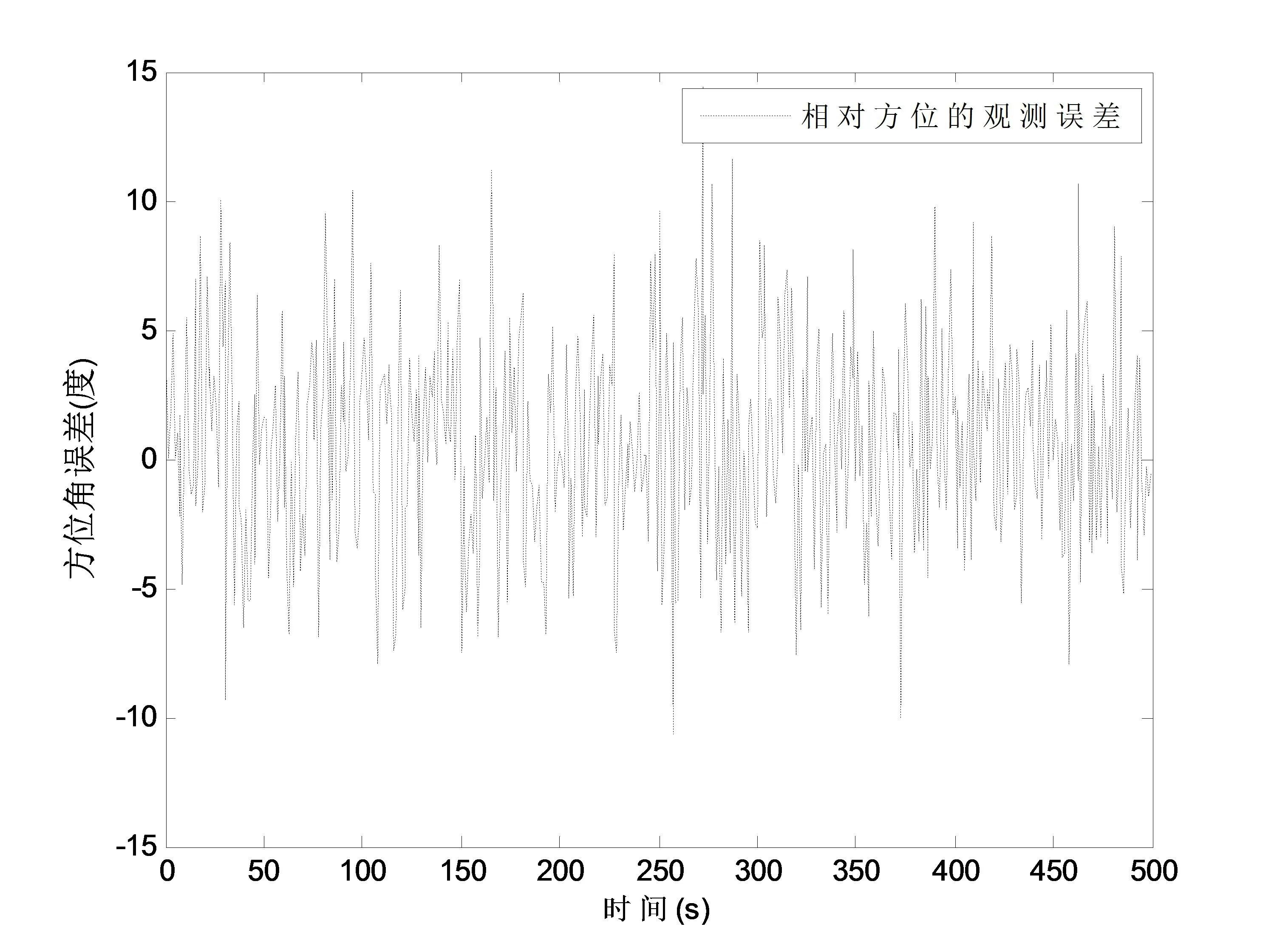
图5 相对方位的观测误差Fig.5 The observation error of relative azimuth

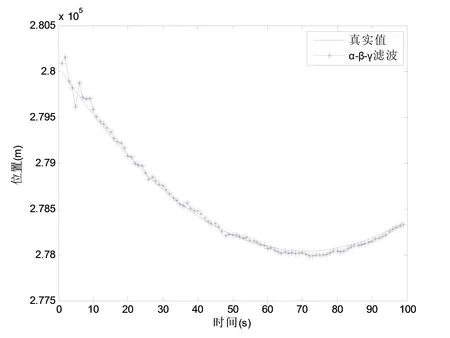
图6 真实值与α-β-γ滤波比较Fig.6 Comparison of the true value and alpha-beta-gamma filtering for the relative distance

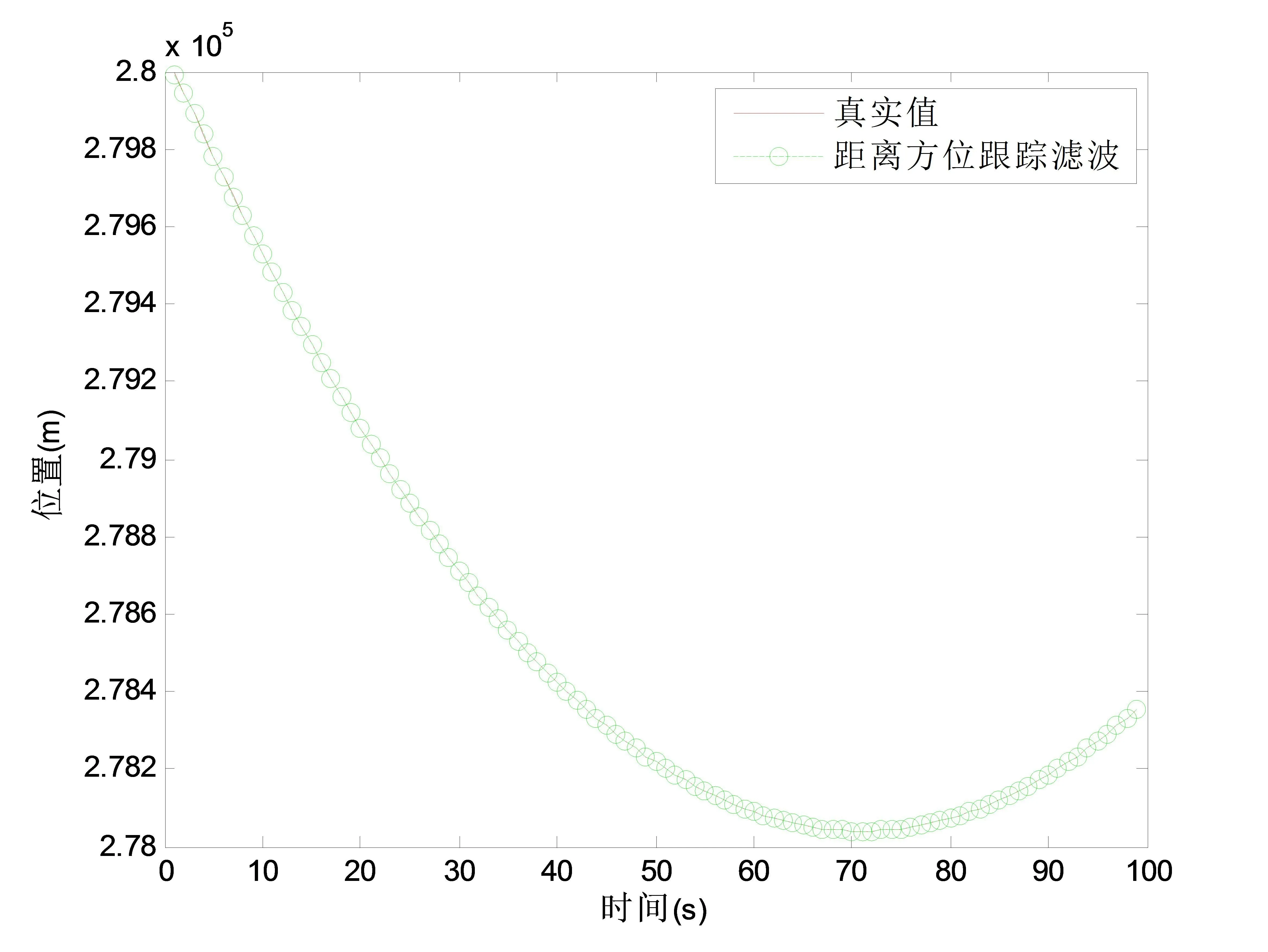
图7 真实值与距离方位跟踪滤波比较Fig.7 Comparison of the true value and range azimuth tracking filtering for the relative distance

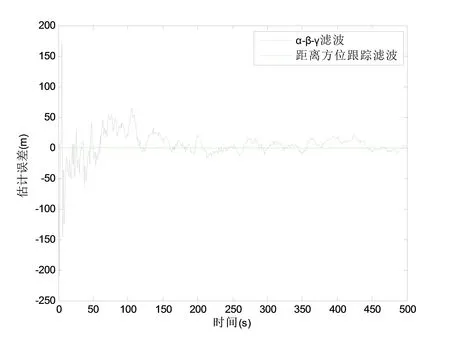
图8 α-β-γ滤波与距离方位跟踪滤波估计误差比较Fig.8 Comparison of the estimation errors between alpha-beta-gamma filtering and range azimuth tracking filtering

由图3到图5的仿真结果，可以明显看出，在整个观测过程中存在过程噪声，相对距离和相对方位观测误差不规律且始终存在；在MATLAB运行后，计算得到的测量方位角下的相对距离的测量方差为100.971 6，误差较大，需要对观测数据进行滤波处理.

由图6与图7的仿真结果，可以明显看出，观测值经过距离方位跟踪滤波后比经过α-β-γ滤波后，更接近真实值.由图8可以看出，虽然观测误差一直存在，但经过滤波后的估计误差逐渐趋于零，滤波的效果明显；且距离方位跟踪滤波产生的估计误差比α-βγ滤波的更快趋于零，波动更小.在MATLAB运行后，计算得到距离方位跟踪滤波后相对距离的均方根误差为0.348 5，而α-β-γ滤波后相对距离的均方根误差为23.454 6，明显看出距离方位跟踪滤波的均方根误差更小，滤波效果更好.

由上述计算机仿真结果可以看出，对匀加速运动的目标进行跟踪时，本文给出的距离方位跟踪滤波算法的估计误差与均方根误差都小于常规的α-β-γ滤波算法.这说明距离方位跟踪滤波算法在跟踪效果上优于常规的α-β-γ滤波算法，这种改进的滤波算法适合于对匀加速运动的(CA模型)目标进行跟踪，跟踪效果较好.

4 结束语

本文在传统的α-β-γ滤波算法的基础上，给出了一种改进的距离方位滤波算法.该算法引入了坐标投影的思想，通过在两机间相对距离的斜面上根据方位角把相对距离在x、y方向进行投影，把三维空间飞机的防撞问题变成了二维斜面上飞机的防撞问题，并利用距离方向和距离正交方向的残差对预测结果进行修正，改善了算法的滤波精度.通过蒙特卡罗仿真实验，验证了这种算法对匀加速运动目标的滤波效果优于常规的α-β-γ滤波算法.本文给出的距离方位滤波算法适用于机载防撞系统中匀加速运动目标的跟踪.