简牍算书一种特殊计算方法解析

周序林，何均洪，李文娟

(1.西南民族大学中国语言文学学院，西南民族大学出土文献研究中心，四川 成都 610041；2.中国民用航空飞行学院大飞机学院，四川 广汉 618307；3.成都工业职业技术学院马克思主义学院，四川 成都 610213)

简牍算书是指在纸张广泛使用之前书写在竹木简牍上的算书文献.目前所见简牍算书属战国秦汉时期，共计六种:北京大学藏秦简《算书》《田书》(均部分刊布)、岳麓书院藏秦简《数》、张家山汉简《筭数书》、双古堆汉简《算术书》(残简)、睡虎地汉简《筭术》(部分刊布)[1-11].简牍算书文献埋藏于地下两千多年，未经转辗传抄，具有无可比拟的文献真实性，因而十分珍贵.这些数学文献真实地反映了中国传统数学在战国秦汉时期发展的原貌，是研究中国早期数学的第一手材料，具有重大数学史价值.

对这些简牍算书文献进行梳理，发现了一种特殊计算方法.这种算法具有明显的凑数的特征，没有算理可言，不具有普适性.我们暂且把这种算法称为“凑数法”.简牍算书中共发现四个使用凑数法的典型例子，分别是:北京大学藏秦简《算书》“里田”“方田”[4]，张家山汉简《筭数书》“里田”[6]，岳麓书院藏秦简207～210所载“赢不足”算题[5].进一步分析发现，以上四例虽然都使用了凑数法，但是每一例的凑数方法又各不相同，可谓凑无定法.下面分为“里田术”中的凑数法和“赢不足”中的凑数法，逐一解析.

1 简牍算书“里田术”中的凑数法

在中国传统数学中，1平方里＝375亩或3顷75亩.将平方里数转化为顷亩数所使用的算法就是“里田术”.传世文献《九章算术·方田》载有“里田术”如下:“广从里数相乘得积里.以三百七十五乘之，即亩数.”[12]设广为a，从为b，平方里数为r，所求顷亩数为x，则此“里田术”可理解如表1.

表1 《九章算术》“里田术”Table 1 The method for fields measured in li in the Nine Chapters on the Art of Mathematics

可见，《九章算术》“里田术”直接使用了“1平方里＝375亩”这一数量关系，而没有讲“375”是如何算得的.简牍算书中则有几种算法讲如何算得“375”，其中北京大学藏秦简《算书》简04-081载有一条“里田术”如下:

●里田述(术)曰:里乘里，一殹(也)，见一鼠(予)二，见二鼠(予)四(四，四)者加一，因而三之，即顷亩殹(也).[4]

《算书》简牍整理者引郭书春先生意见阐释了这段术文的文意[4]，日本学者也进行了解释[13]，其中，后者的理解更贴近简文原意.简文“见”即“现”字，义为“出现(在筹算板上)”.简文“鼠”即“予”字.据里耶秦方8-461第XIII行“鼠如故，更予人”[14]，“给予”之“予”作“鼠”是秦始皇推行“书同文字”政策之前的用字，“书同文字”政策之后“给予”之义的“鼠”字改作“予”.“予”，这里指把算筹放置到筹算板上，即设置算筹.“予二”“予四”分别指在筹算板上设置算筹“二”“四”.术文“四者加一”意为“4＋1”.术文“三之”是“数词＋之”的结构，表示相乘关系，代词“之”在这里指术文前文“里乘里，一殹(也)，见一鼠(予)二，见二鼠(予)四(四，四)者加一”所产生的运算结果.上引《算书》“里田术”可解析如表2.

表2 《算书》简04-081“里田术”Table 2 The method for fields measured in li on slip 04-081 of the Suanshu

表2算得“125”的过程，即步骤一(2)(3)(4)，显然是在凑数，没有算理可言，不具有普适性.这种凑得“125”的方法，在张家山汉简《筭数书》“里田术”中却又不同.张家山汉简《筭数书》简189～190载有一条“里田术”如下:

里乘里(里，里)也，因以里之下即予廿五，因而三之，亦其顷亩数也.[6]

学界认为此术文有脱文，并提出了不同理解[15-20]；[日]张家山汉简『算数书』研究会认为，简文“因以里之下即予廿五”意为在1平方里的下面付与25[21]，此说可从.此术文可解析如表3.

表3算得“125”的过程，即步骤一(2)，也没有算理可言，同样不具有普适性，也是在凑数.古人为什么要如表2步骤一(2)(3)(4)、表3步骤一(2)这样凑数?其意义何在?我们暂时不得而知.

表3 《筭数书》简189～190“里田术”Table 3 The method for fields measured in li on slips 189～190 of the Suanshu shu

简牍算书中还有一种使用更为普遍的“里田术”，这种“里田术”在不同的简牍算书中有不同的表达，但是算法相同.以岳麓书院藏秦简《数》简62所载“里田术”为例:

里田述(术)曰:里乘里(里，里)也，因而参之，有(又)参五之，为田三顷七十五亩.[5]

术文“参之”的“之”指代“1里×1里”的乘积，“参之”意为“3×1”，“参五之”的“参五”意为“3次用5乘”，“之”指代“参之”的运算结果.上引“里田术”可解析如表4.

表4 《数》简62“里田术”Table 4 The method for fields measured in li on slip 62 of the Shu

表4算得“375”的过程，即步骤二、三，也带有凑数的特征，不过所凑之数“5”“5”“5”“3”是有出处的，是对“375”进行分解而来.我们推测，将375作如上分解，是为了简化当平方里数较大时可能会出现的复杂计算.同理，表2与表3通过“125×3”算得“375”的过程，即步骤二，也具有凑数的特征，其中的“3”与“125”也是源于对“375”的分解.当然，简牍算书也有“里田术”与《九章算术》“里田术”一样直接使用“375”进行运算的，目前仅见于张家山汉简“里田术”简190“广一里、从一里为田三顷(七十)五亩”[6].可见，凑数法在简牍算书“里田术”中有较广泛运用.

2 简牍算书“赢不足”中的凑数法

凑数法除了见于简牍算书“里田术”外，还出现在与“盈不足术”相关的术文或算题中.岳麓书院藏秦简207～210载有“赢不足”算题如下:

算题解析如下:10斗稻、10斗粢、10斗菽的价格分别是9钱、7钱、5钱，假如买这3种食粮共计10斗花费8钱，问这3种食粮各多少斗.答案:稻6斗，粢3斗，菽1斗.计算方法:首先在筹算板上设置诸数图1，然后计算如下:

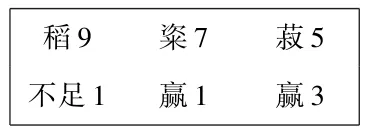
图1 设置诸数Fig.1 Putting down the given amounts on the counting board

稻的斗数:(稻不足1×稻9＋菽3×粢7)÷(稻不足1＋粢赢1＋菽赢3)＝6

粢的斗数:(菽3×菽5)÷(稻不足1＋粢赢1＋菽赢3)＝3

菽的斗数:(稻不足1×菽5)÷(稻不足1＋粢赢1＋菽赢3)＝1

本算题运用现代数学的方法，设稻、粢、菽斗数各为x、y、z，则得方程组:

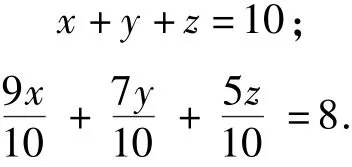
由两个方程式组成的方程组里出现了3个未知数，构成了3元1次方程，显然不能求解.令人惊奇的是，古人通过术文所提供的计算方法算得了答案.不过，古人的方法没有算理可言，正如有学者指出:“此计算不具有普遍性，而且有明显的算理错误.”[22]“(运算)数据于算题术文吻合，但不能解释其数学含义.”[23，24]“各实的计算步骤，没有规则可言，整个计算也看不出有什么道理.”[5，24]古人所用的方法，就是在凑数，正如有学者指出:“古人在设计这个问题的时候，可能就是先有答案和题设，然后拟合术文的.”[5，24]

与“盈不足”相关的凑数法还见于北京大学藏秦简《算书》“方田术”:

简文“即幷赢、不足以为法”后省略了被除数的计算方法(即:16×15＋15×16)；简文“有(又)耤丗一分十五，令韋(維)乘上十五”(意即:×15)后有省略，所省略的简文表达的是再做一次“×15”运算.整条术文的大意是，首先运用“盈不足术”求得正方形田块(240平方步)的边长(15步)，然后用所得边长(15步)验算如何算得正方形田块面积(240平方步).其中验算的思路据术文可示意如图2.现将上引“方田术”解析如表5.

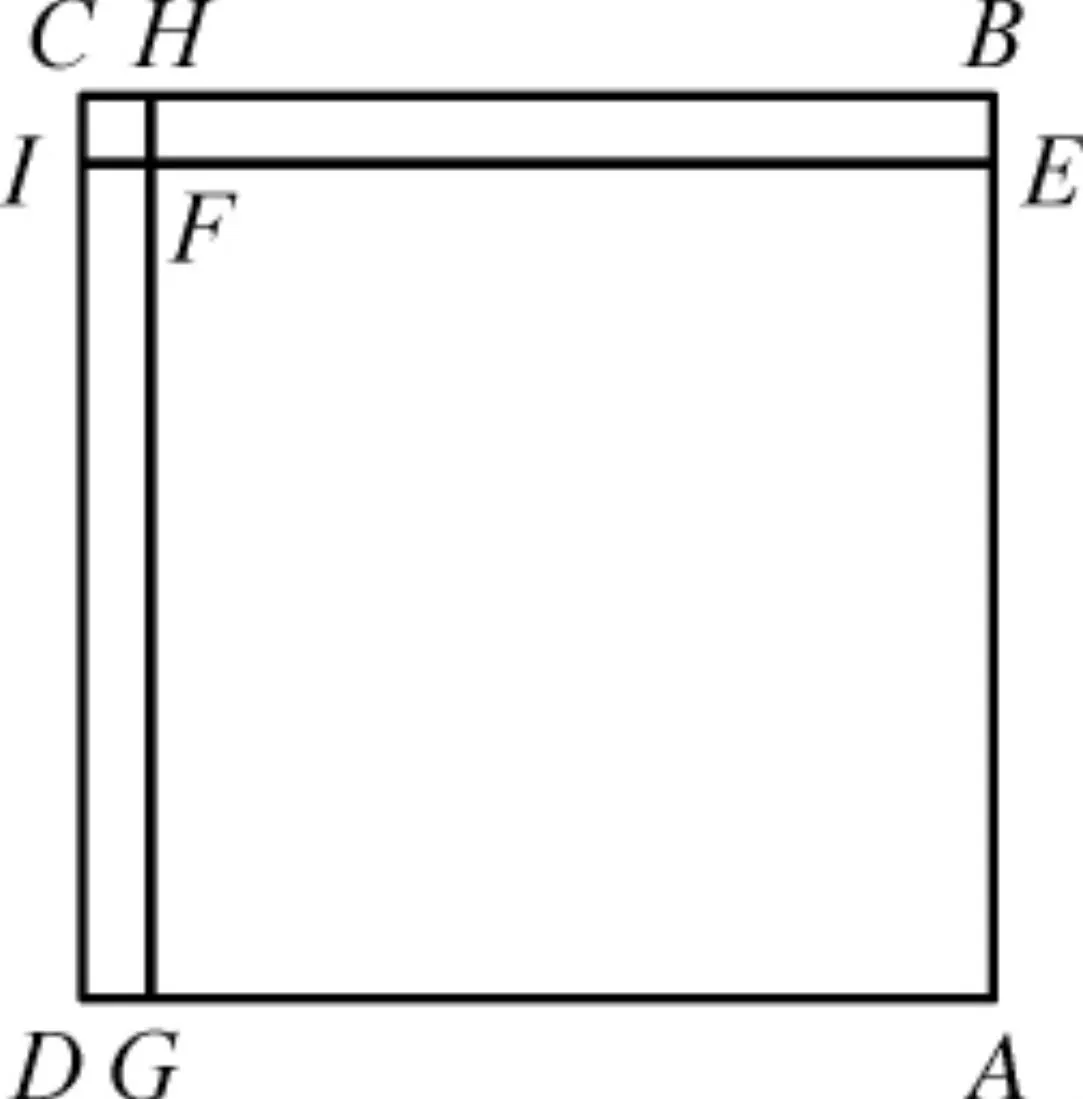
图2 “方田术”验算思路Fig.2 Reverse engineering the computation in the method for square fields

表5 《算书》“方田术”Table 5 The method for square fields in the Suanshu

3 结语

简牍算书中的凑数法，应该是古人在设计术文之前就已知答案的情况下对术文数据进行拟合的结果，这种特殊算法不具算理，也不具普适性.简牍算书中存在凑数法，表明中国传统数学在战国秦汉时期还处于发展的早期阶段，这一特殊算法随着中国传统数学的发展而消亡，不见于《九章算术》等传世数学文献.对这种凑数法进行研究，有助于正确解读简牍算书某些算题，有利于简牍算书文献整理研究，有助于呈现并认识中国传统数学在战国秦汉时期发展的原貌，这说明简牍算书文献在研究中国数学史方面具有重要意义和巨大价值.

致谢:本文写作得到美国纽约市立大学(City University of New York)道本周(Joseph Warren Dauben)教授帮助，谨致谢忱.