基于免疫疗法建立胰腺癌模型的稳定性分析

李梅梅，冀小明，刘玲伶

(1.西南石油大学理学院，四川 成都 610500；2.西南民族大学预科教育学院，四川 成都 610041)

癌症是威胁人类健康的一类重大疾病，其发病率持续升高.据统计，2018年全世界新发癌症约1 810万例，死亡约960万例[1].其中胰腺癌是最致命的癌症之一，其致死率与发病率几乎一致，5年总生存率仅约9%[2].根据美国癌症协会最新数据显示，2019年新增胰腺癌患者约56 000例，死亡患者约45 000例[3]，到2030年，胰腺癌或将成为恶性肿瘤中的第2位致死原因[4].目前在胰腺癌的治疗中比较关注的是采用免疫治疗，它的目的是通过刺激患者的免疫系统，触发抗肿瘤免疫反应，最终依靠自身能力更好地识别并杀死癌细胞.数学模型可动态表示肿瘤细胞和免疫细胞之间的相互作用，考虑不同因素的影响建立恰当的胰腺癌数学模型，分析模型的定性性质，有助于更深入地了解肿瘤发病机理，为探索肿瘤的治疗方案线索和建议.

1994年Kuznetsov[5]等人提出了肿瘤细胞和效应细胞相互作用的二维常微分方程组，通过与实验数据的比较，得到在体内无法测量的参数的数值估计，分析出该模型发生了鞍结分岔和跨临界分岔，有助于指导解释肿瘤躲过免疫系统，发生偷偷“逃逸”现象，预测出肿瘤的生长过程及其临床表现会在3-4个月的周期内复发；1998年Kirschner和Panetta[6]建立了描述肿瘤细胞、效应细胞和细胞因子之间相互作用的三维常微分方程组，通过对平衡点的稳定性和分岔分析，解释肿瘤大小的短周期振荡和长期肿瘤复发，探索了过继细胞免疫治疗对模型的影响，并描述了肿瘤可以被消除的情况；2014年Louzoun[7]等人建立了四维胰腺癌模型，利用该模型定性地解释各种生物医学和临床数据，结果表明肿瘤生长速度受到肿瘤细胞、内皮细胞和免疫反应之间复杂的反馈回路的影响，不同回路的相对强度决定了癌症的生长速度及其对免疫治疗的反应；2016年Li和Xu[8]提出了脉冲免疫疗法与胰腺癌和免疫系统相互作用的模型，通过对无瘤平衡点的不稳定性和高肿瘤平衡点的稳定性分析，证实进行免疫治疗比不进行免疫治疗对胰腺癌患者的预后更好；2017年He和Xu[9]扩展了Li和Xu[8]的模型，增加了调节性T细胞，得出T细胞可调节效应细胞，使其无法有效地发挥细胞毒性，导致效应细胞对肿瘤细胞的免疫反应减弱或不存在；2019年Hu[10]等建立了一个包括胰腺癌细胞，胰腺星状细胞，效应细胞和肿瘤促进和肿瘤抑制细胞因子的五维非线性常微分方程组，通过参数的局部敏感性分析得出存在一个前肿瘤细胞因子的临界激活率，超过这个激活率，应用四种免疫细胞过继转移，癌症可以被根除的结论.本文是基于Hu[10]等工作进行定性分析，将模型无量纲化，分析标度后系统平衡点的存在性和稳定性.

1 方法

2019年Hu[10]等建立的五维非线性常微分方程组为:

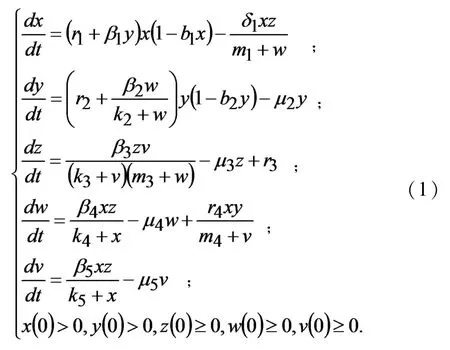
其中x，y，z，w，v分别代表胰腺癌细胞(PCC)、胰腺星状细胞(PSC)、效应细胞(包括CD8＋T细胞NK细胞)、促进肿瘤细胞因子(包括TGF-β和IL-6)的浓度和抑制肿瘤细胞因子(包括IFN-γ和IL-2)的浓度，各参数及其生物意义见表1.Hu[10]等人通过(1)式中参数的局部敏感性分析得出存在一个前肿瘤细胞因子的临界激活率，超过这个激活率，应用四种免疫细胞过继转移，癌症可以被根除的结论.并运用最优控制理论来寻找最好的过继细胞免疫疗法，得出单免疫治疗不可能控制胰腺癌，而抗TGF-β和免疫细胞过继转移联合免疫治疗可以延长患者生存期.

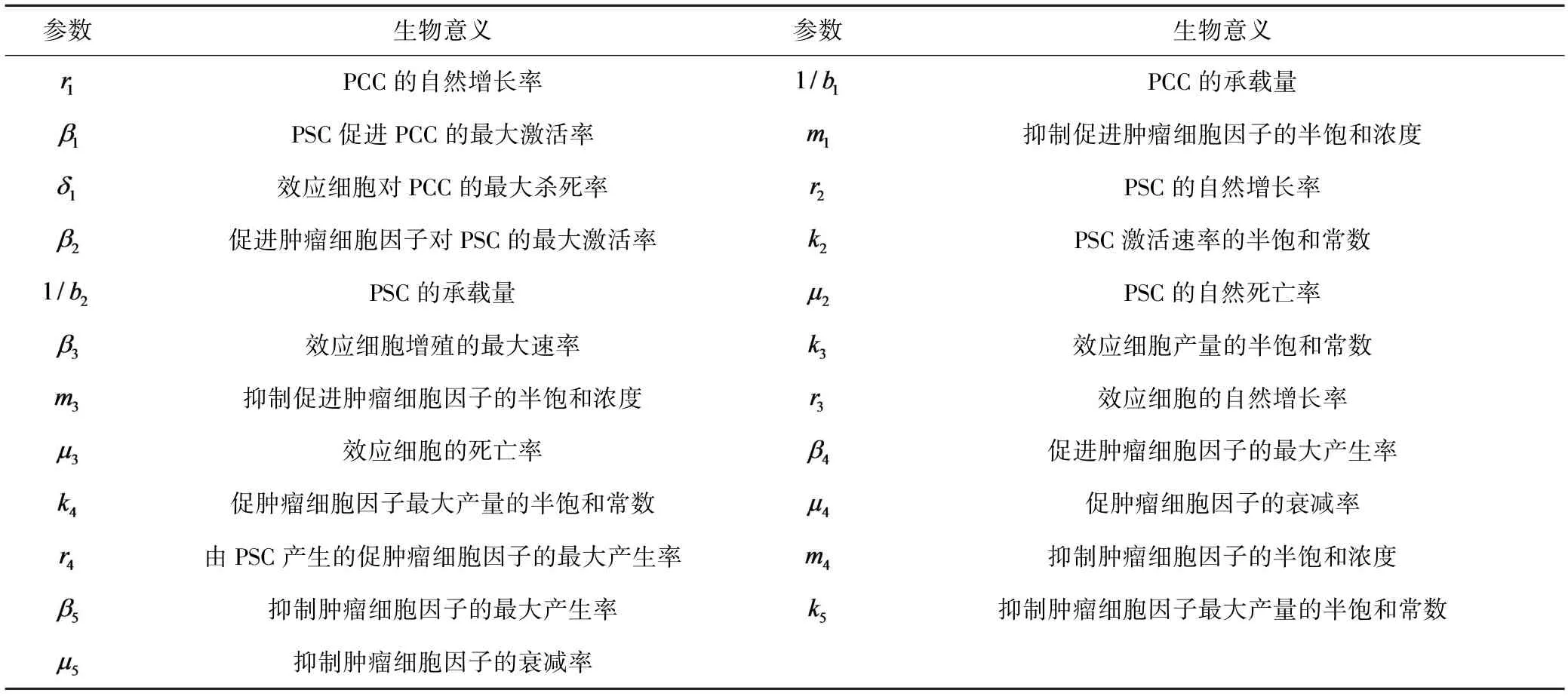
表1 各参数及生物学意义Table 1 Parameters and their biological meanings

本文利用Lyapunov稳定性理论和解析计算法对模型动力学进行分析.首先，我们对系统(1)进行无量纲化，然后对标度后的系统进行稳态分析，讨论系统的无病平衡点和地方病平衡点，并对其稳定性进行分析，给出模型稳定性的充要条件，进一步探索免疫治疗对模型的影响.记x＝(1/b1)X；y＝(1/b2)Y；z＝r3Z；w＝m3W；v＝k3V，则(1)式化为

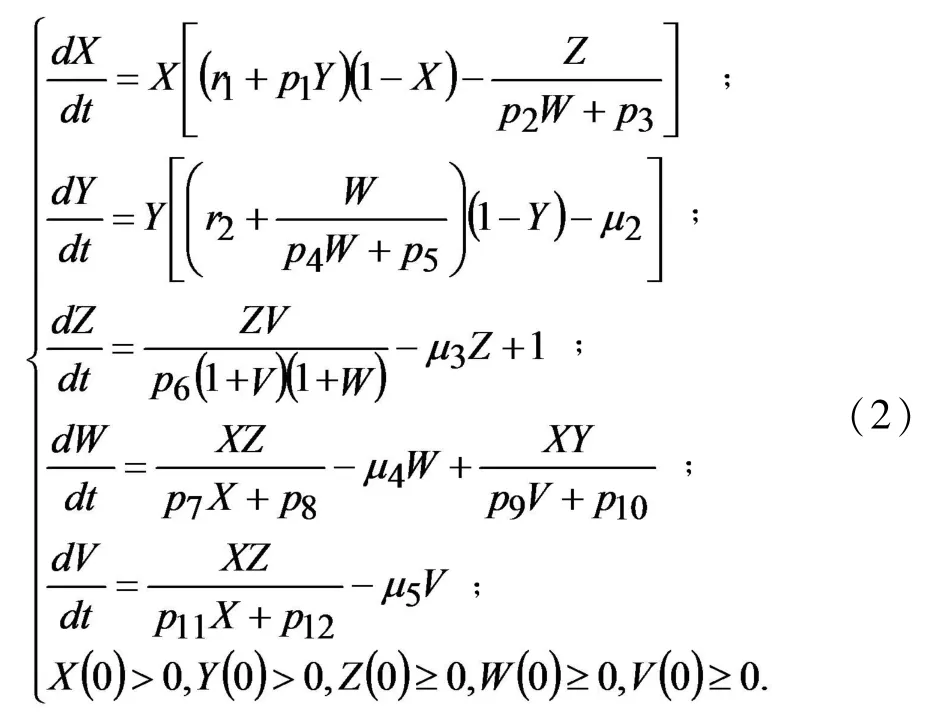
2 分析

2.1 平衡点分析

首先采用解析法求解模型(2)的平衡点，见定理1.

定理1对于系统(2)，时存在唯一无病平衡点，当，除外还存在无病平衡点；当时，存在无病平衡点和地方病平衡点，其中X*由方程μ4(p7X＋p8)(l1X7＋l2X6＋l3X5＋l4X4＋l5X3＋l6X2＋l7X＋l8)＝0的非负解确定并且满足且

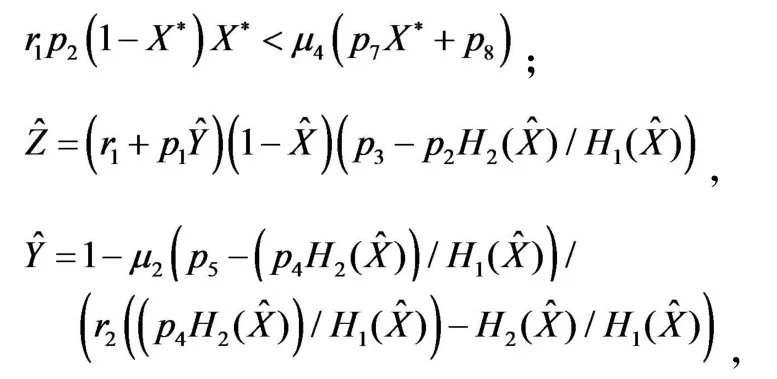
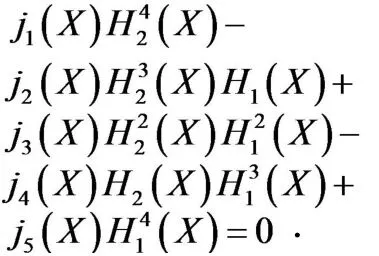
证系统(2)的平衡点由下列方程组

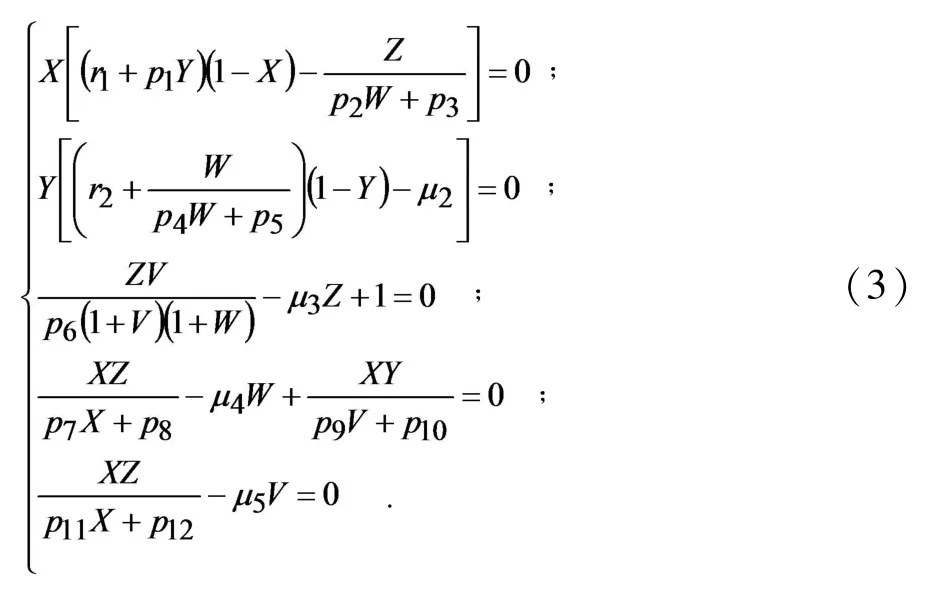
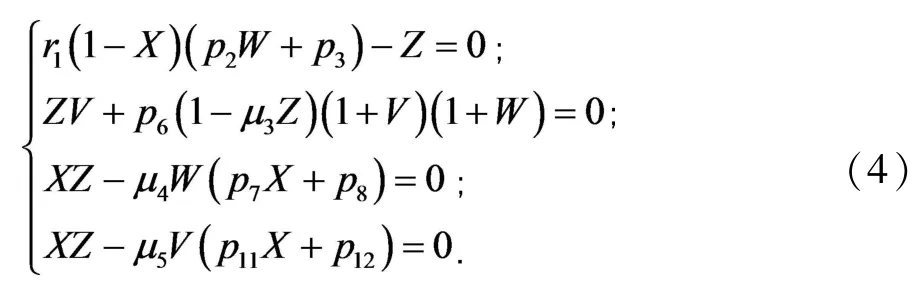
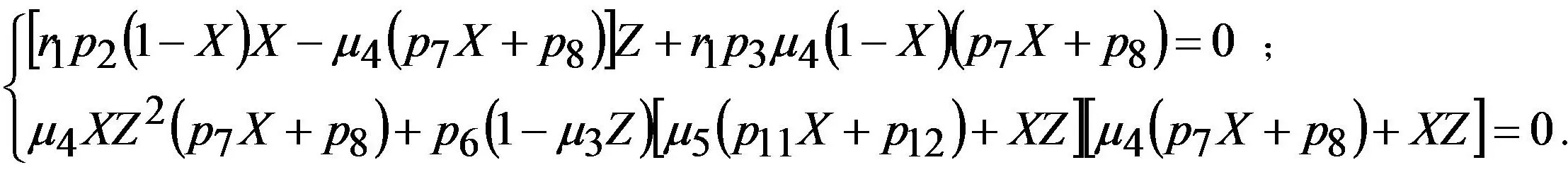
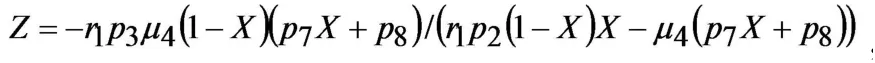
将其代入第二个方程中整理有

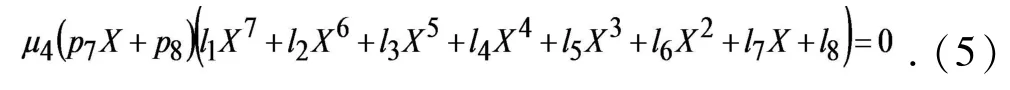
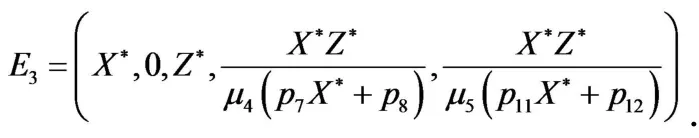
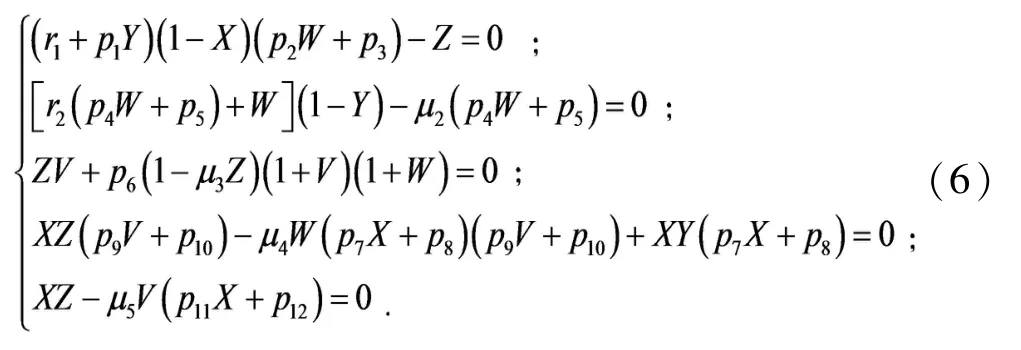
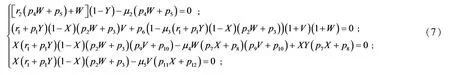
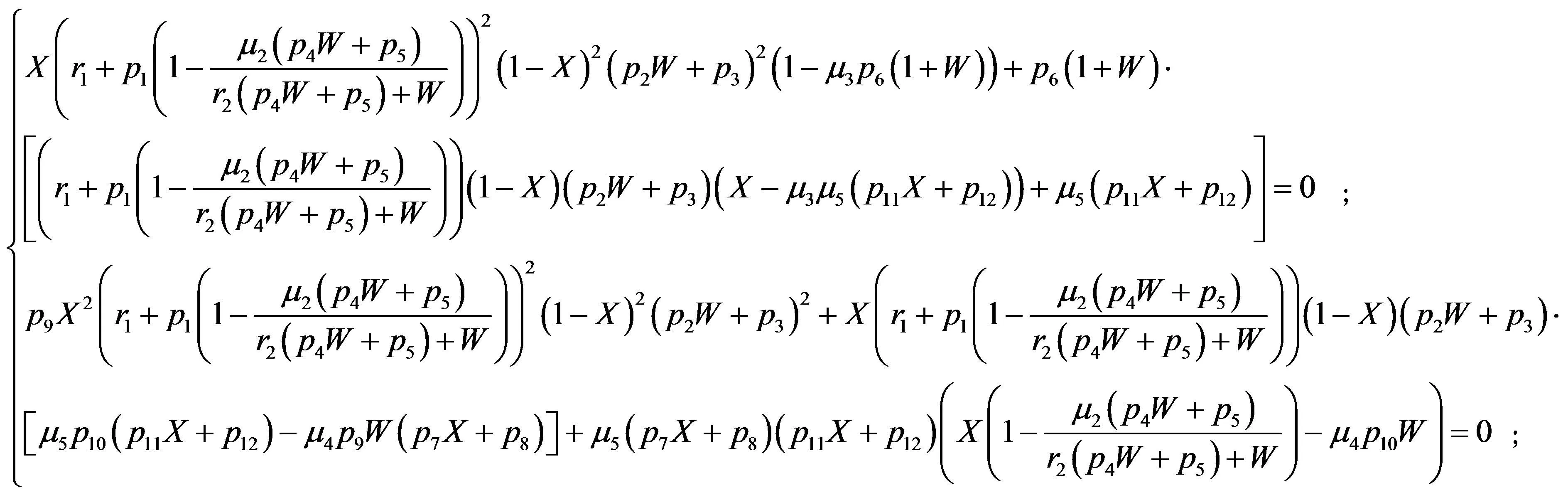
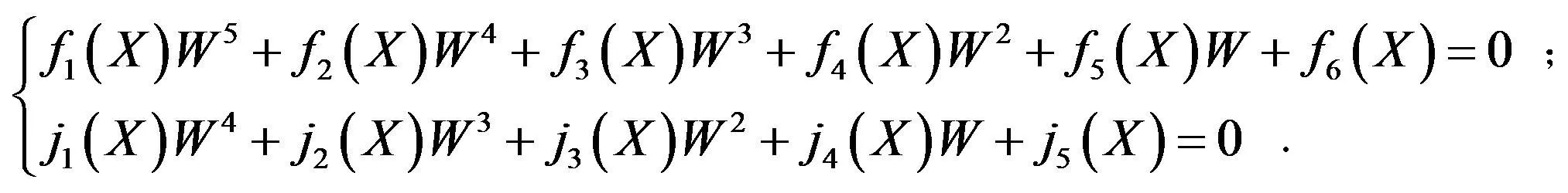
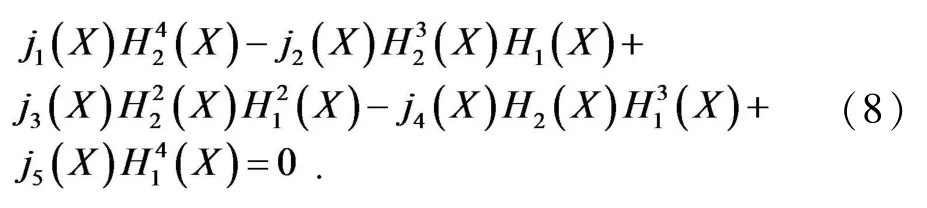
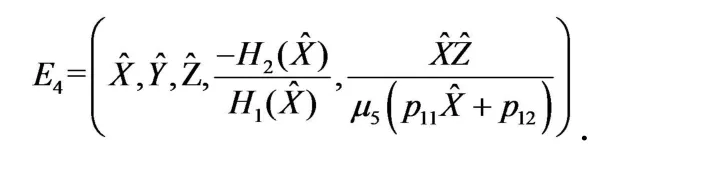
证毕.

注1由于系统高度非线性，我们无法给出平衡点的解析表达式.下面采用数值方法来讨论时平衡点的存在性.参数值源于文献[10]，将参数值代入(5)式中求得唯一正解于是存在无病平衡点.将参数值代入(8)式中求得唯一正平衡点于是存在地方病平衡点

注2利用Maple软件对和整理代码如下:

F1:＝X*(r[1]＋p[1]*(1-mu[2]*(W*p[4]＋p[5])/(r[2]*(W*p[4]＋p[5])＋W)))＾2*(1-X)＾2*(W*p[2]＋p[3])＾2*(1-mu[3]*p[6]*(1＋W))＋p[6]*(1＋W)*((r[1]＋p[1]*(1-mu[2]*(W*p[4]＋p[5])/(r[2]*(W*p[4]＋p[5])＋W)))*(1-X)*(W*p[2]＋p[3])*(X-mu[3]*mu[5]*(X*p[11]＋p[12]))＋mu[5]*(X*p[11]＋p[12]))；

F2:＝p[9]*X＾2*(r[1]＋p[1]*(1-mu[2]*(W*p[4]＋p[5])/(r[2]*(W*p[4]＋p[5])＋W)))＾2*(1-X)＾2*(W*p[2]＋p[3])＾2＋X*(r[1]＋p[1]*(1-mu[2]*(W*p[4]＋p[5])/(r[2]*(W*p[4]＋p[5])＋W)))*(1-X)*(W*p[2]＋p[3])*(mu[5]*p[10]*(X*p[11]＋p[12])-mu[4]*p[9]*W*(X*p[7]＋p[8]))＋mu[5]*(X*p[7]＋p[8])*(X*p[11]＋p[12])*(X*(1-mu[2]*(W*p[4]＋p[5])/(r[2]*(W*p[4]＋p[5])＋W))-mu[4]*p[10]*W)；

collect(numer(F1)，W)；collect(numer(F2)，W)；

q1:＝W＾5*f[1]＋W＾4*f[2]＋W＾3*f[3]＋W＾2*f[4]＋W*f[5]＋f[6]；

q2:＝W＾4*j[1]＋W＾3*j[2]＋W＾2*j[3]＋W*j[4]＋j[5]；

q3:＝prem(q1，q2，W)；q4:＝prem(q2，q3，W)；q5:＝prem(q2，q4，W)；

q6:＝collect(q5，W)；W:＝-H[2](X)/H[1](X)；

f2:＝j[1](X)*W＾4＋j[2](X)*W＾3＋j[3](X)*W＾2＋j[4](X)*W＋j[5](X)；numer(f2)；

2.2 稳定性分析

下面给出平衡点稳定的充要条件.

定理2当且时，无病平衡点E1渐近稳定；当且时，无病平衡点E1不稳定；当且时，无病平衡点和均不稳定；当且时，无病平衡点不稳定，无病平衡点渐近稳定.

证在平衡点处的Jacobian矩阵为

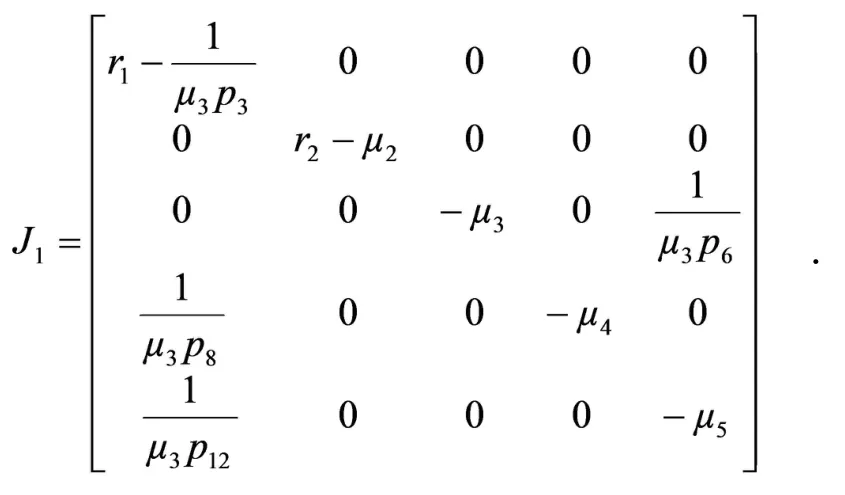
特征值为

证毕.

注3由定理2知当且，说明此时PSC细胞的自然死亡率大于内在增长率，它对癌细胞的促进作用小于效应细胞对癌细胞的抑制作用，无病平衡点E1存在且渐近稳定，这是患癌的一个早期状态，此时在理想情况下除了效应细胞在增长外，其余细胞的增长率都为0，癌细胞处在一个稳定的状态，这时如果及时发现并进行药物和手术的干预，会有“治愈”癌症的可能；当且时，无病平衡点E1不稳定，说明细胞因子对癌细胞的促进作用大于效应细胞对癌细胞的抑制作用，此时癌细胞有了扩散的可能，当psc细胞的自然死亡率小于内在增长率时，癌细胞开始扩散，这表明若不经治疗，癌细胞会继续生长，当时，无病平衡点E2稳定，此时也是一个很好的治疗时期，否则当时，无病平衡点E2变得不稳定，会继续进行扩散，治疗的难度也将加大.

注4参数值取文献[10]中的值，E3处的特征值为，由于，于是无病平衡点渐近稳定.在地方病平衡点处的特征值为，由于存在，于是地方病平衡点E4不稳定.根据数值法求出的无病平衡点E3和地方病平衡点E4的稳定性表明癌细胞在扩散之前会有一个稳定阶段，那么在这些阶段进行治疗是比较好的时机，但癌细胞也会不断地扩散，并且不稳定极易复发，给治疗带来了很大的困难，所以建立数学模型，根据模型的定性性质，及早排查发现进行阶段治疗，是非常有必要的.

3 数值模拟

利用Matlab进行数值模拟验证，参考文献[10]中参数的取值，以及定理1，2中且的要求，取参数为，初 值 取，从图1中可以看到无病平衡点E1存在，并且是不稳定的，当初值取，在图2中看到地方病平衡点存 在 且 不 稳 定；根 据 定 理1，2中且的要求，取参数为初值条件取，在图3中看到无病平衡点存在且渐近稳 定，初 值 取，在图4中看到无病平衡点E3存在且渐近稳定.

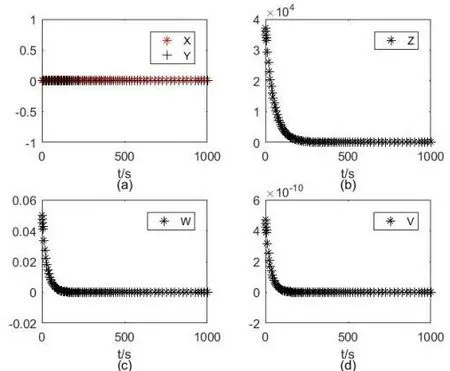
图1 平衡点E1存在且不稳定Fig.1 The equilibrium E1 exists and is unstable

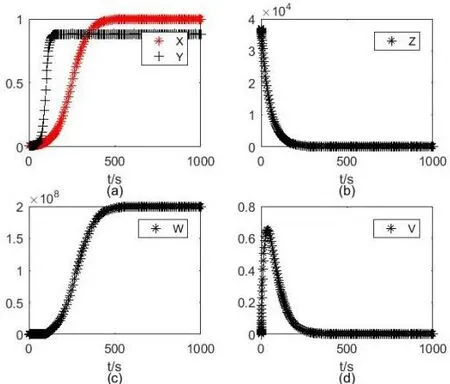
图2 平衡点E4存在且不稳定Fig.2 The equilibrium E4 exists and is unstable

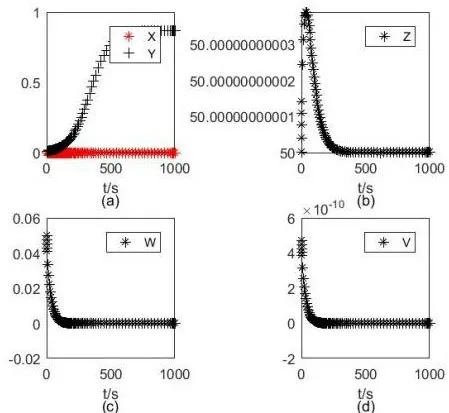
图3 平衡点E2存在且渐近稳定Fig.3 The equilibrium E2 exists and is asymptotically stable

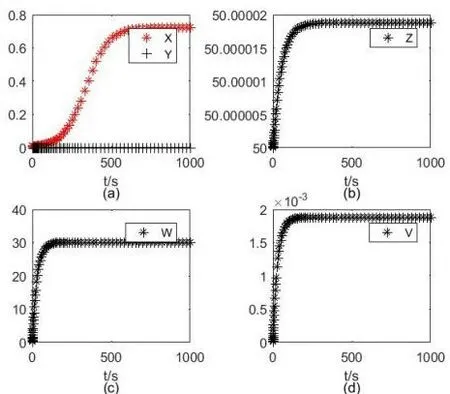
图4 平衡点E3存在且渐近稳定Fig.4 The equilibrium E3 exists and is asymptotically stable

4 结论

根据定理2可知当μ2＞r2且r1μ3p3＜1时，说明此时胰腺星状细胞的自然死亡率大于内在增长率，它对癌细胞的促进作用小于效应细胞对癌细胞的抑制作用，无病平衡点E1存在且渐近稳定，这是患癌的一个早期状态，此时在理想情况下除了效应细胞在增长外，其余细胞的增长率都为0，癌细胞处在一个稳定的状态，这时如果及时发现并进行药物和手术的干预，这个时刻的治疗效果最好，会有“治愈”癌症的可能，是很重要的一个阶段；当μ2＞r2且r1μ3p3＞1时，无病平衡点E1变成了不稳定的，说明此时细胞因子对癌细胞的促进作用大于效应细胞对癌细胞的抑制作用，此刻癌细胞已经有了扩散的可能，当胰腺星状细胞的自然死亡率小于内在增长率时，癌细胞开始扩散，这表明若不经治疗，癌细胞会继续生长；当时，无病平衡点E2稳定，此时也 是一个很好的治疗时期，否则当时，无病平衡点E2变得不稳定，会继续进行扩散，治疗的难度也将加大.所以，对于癌症的早期筛查就显得非常重要，必须抓住癌症扩散前的关键时机及时治疗.

所以通过建立数学模型，可以展示疾病的动态过程，帮助了解发病原理，为疾病的筛查和预防提供指导；通过分析模型的定性性质，为疾病的治疗方向带来思路，具有深刻的意义.通过对胰腺癌模型的稳定性分析得出免疫治疗可以提高效应细胞对癌细胞的抑制作用，减缓促进肿瘤细胞因子的生长速率，降低癌细胞扩散的程度，使其处于相对比较低的地方病平衡点上，是一种相对较好的治疗胰腺癌方法.