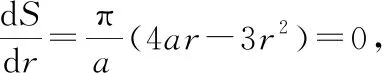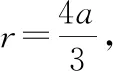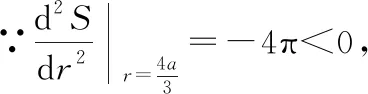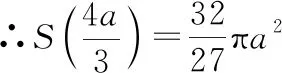空间解析几何中极值问题的求解技巧

◎杨丽娜

[中国石油大学(北京)理学院数学系，北京 100000]

空间解析几何是高等数学的重要内容之一，也是学习多元微积分的基础空间解析几何的极值求解是一种综合题型，考查相关几何知识和取得极值的必要条件下面本文针对四种最值问题分别给出求解方法

一、异面直线最短距离

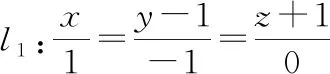
(方法一)与的参数式如下：

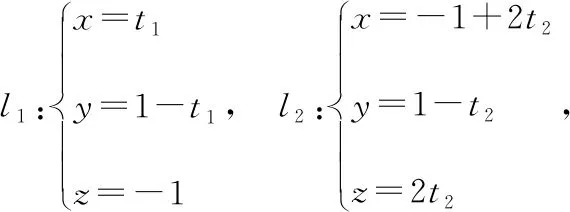
与是与上的任意两点，则：

(,)=(-2+1)+(-)+(2+1)

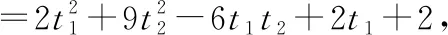
则(,)取得极值的必要条件是：

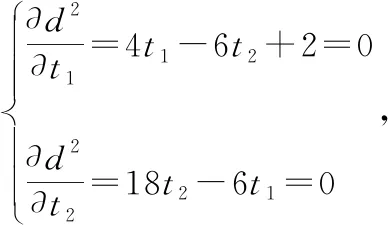
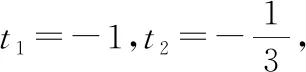
解得的距离为1，即两条直线间的最短距离

(方法二)过作平行于的平面，该平面法向量可取为：

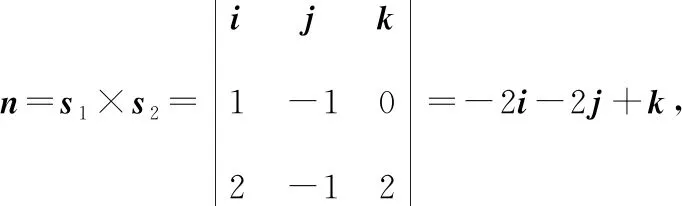
又平面过点(0,1,-1),该平面方程可写为：

-2-2(-1)++1=0，即2+2--3=0，

上的点(-1,1,0)到此平面的距离为1，即所求最短距离

(方法三)和的公垂线的方向向量与、垂直，所以有：

=×,⟹=,

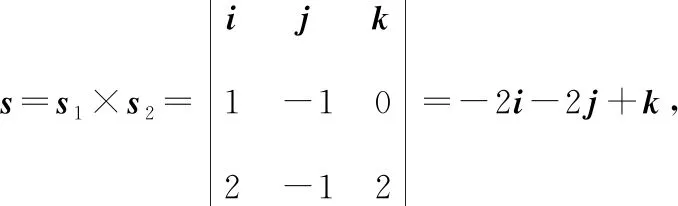
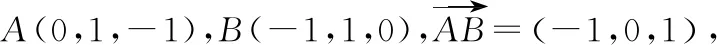
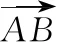
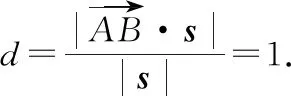
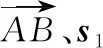
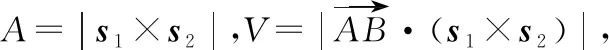
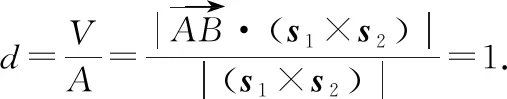
二、曲面与平面的最短距离

2求旋转曲面=+与平面+-2=2之间的最短距离

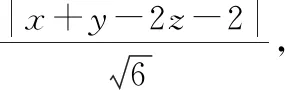
构造拉格朗日函数：

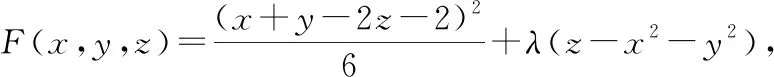
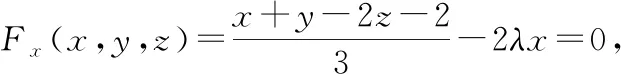
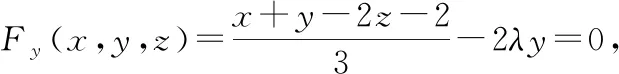
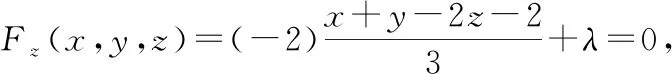
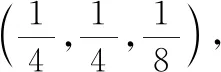
(方法二)在旋转曲面上找一点，使得该点处的切平面平行于已知平面，则该点到已知平面的距离即所求

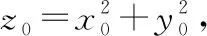
切平面的法向量为(2,2,-1),

曲面在此点处的切平面与已知平面平行，两个平面的法向量也平行，则有：

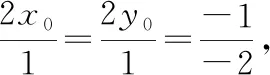
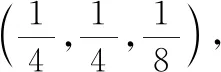
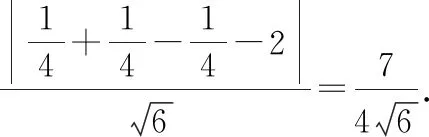
三、求立体体积最值

3已知抛物面=4++的切平面为π，求抛物面上一点，使得介于π、柱面(-1)+=1以及平面=0之间的立体体积最大

设=4++的切点为(,,)，

则π的法向量为(2,2,-1)，

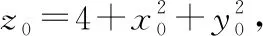
2(-)+2(-)-(-)=0，

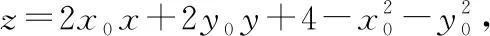
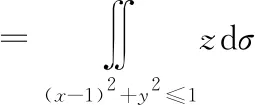
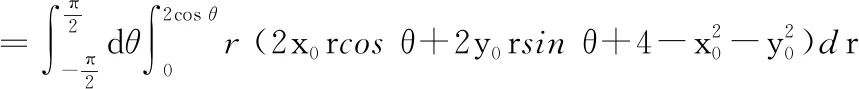
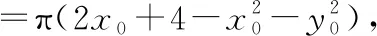
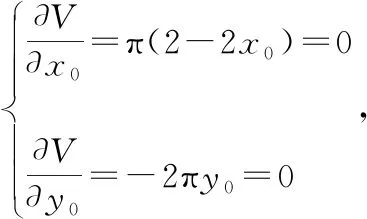
可得驻点(1,0)，且|=5π,=5，

由于实际问题有解，且驻点唯一，所以当切点为(1,0,5)时，所求体积最大

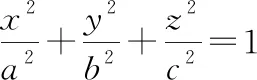
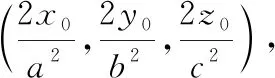
在该点处的切平面方程为：

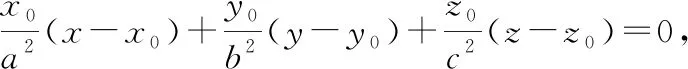
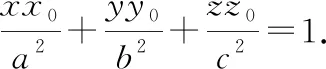
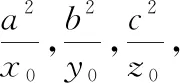
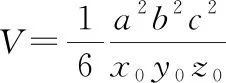
求体积的最小值即求分母的最大值，构造拉格朗日函数：

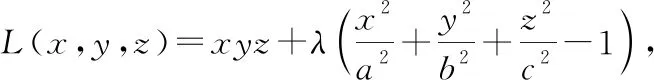
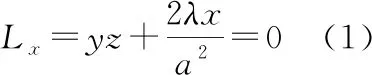
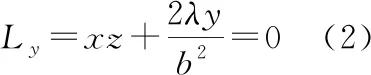
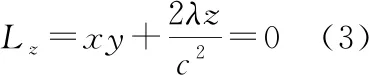
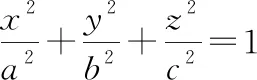
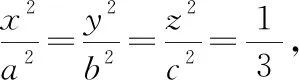
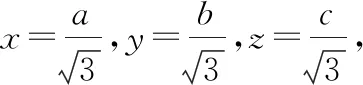
四面体体积最小值为：

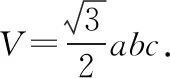
对于空间解析几何的最值问题，我们可以应用条件极值或无条件极值求解，如果最值问题涉及空间曲面的切平面，则切点的坐标是求解的关键

四、求表面积的最值

5设半径为的球的球心在半径为(为常数)的定球面上，为了使前者夹在定球内部的表面积最大，求，并求此最大表面积

设定球的球心在原点，其方程为：

++=，

动球的球心在定球面上，由于对称性，设动球的球心在定球面与轴的交点(0,0,)处，则动球面的方程为：

++(-)=，

两球面的交线为：

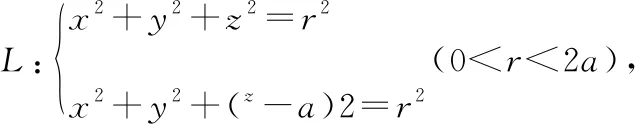
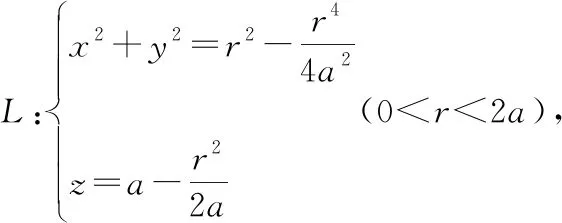
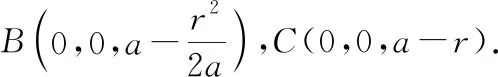
把动球面看作平面曲线：

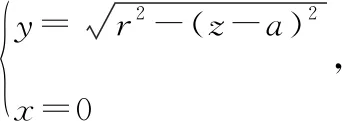
绕着轴旋转得到的旋转曲面，夹在定球面内部的那部分曲面的面积为：

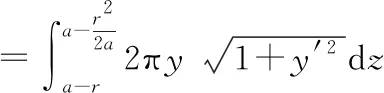
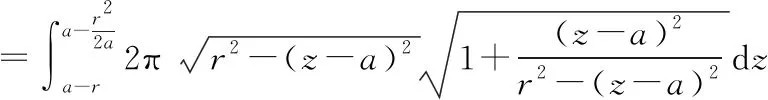
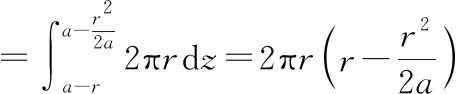
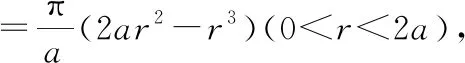
根据一元函数取得极值的必要条件：