优化数学实验，凸显数学本质——以人教版“用频率估计概率”教学为例

◎石锦彪

(广东省珠海市斗门区莲洲镇莲溪学校，广东 珠海 519135)

曾经有一名学生拿着一道有关“用频率估计概率”的数学题问我，题目如下：

小新抛一枚质地均匀的硬币，连续抛2次，第一次硬币落地为正面朝上，那么第二次抛硬币，硬币反面朝上的概率为( )

A.0 B.0.25 C.0.5 D.1

学生选择了D，据他的理解，根据“用频率估计概率”知识，硬币正、反面朝上的概率都是05，既然第一次是正面，那么第二次肯定是反面，所以概率是1虽然学生的理由貌似充分，但显然学生对课本的实验和大数定律存在一定的误解

1 教材实验分析

教材的实验是以抛掷硬币为主，分别统计“正面向上”和“反面向上”的频数与频率，通过学生实验、观察、记录、归纳出大数定律然而，“抛掷硬币”实验过于单调，重复而简单，学生容易产生厌倦感，易出现随意应付，乱填实验数据的情况，从而影响实验结果

笔者对实验的材料进行筛选，发现概率起源于赌博，故设计了一个实验——骰子大小，这不仅能提高学生的学习兴趣，还能在学科教学中渗透德育教育——禁赌教育

2 教学实验设计

本节课是数学实验探究课，所以教师对于实验设计应花心思，重过程，使趣味性与实用性相结合，培养学生的数学实验和数据分析素养本次数学实验以“投骰子买大小”为模拟背景，设计模拟场景，让学生通过实际操作，感受大数定律的适用条件，并体会为什么可以用频率估计概率生动的实验能吸引学生的注意，把实验的重复性和单调性冲淡，同时进行禁赌教育，把德育教育融入学科教育中具体操作流程如图1所示

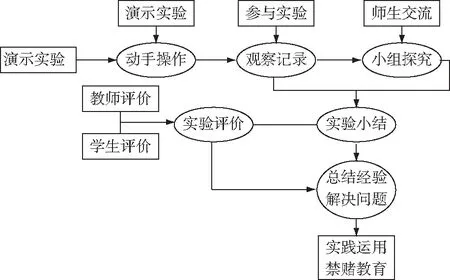
图1

3 教学实验过程

3.1 课前预习，熟悉流程

教师在上课前一天布置预习任务，让学生了解投骰子的规定；并在班级群上传演示实验的视频，让学生熟悉实验的流程和注意事项教师提前准备实验器材，确保当天实验物资充足学生了解实验具体要求和操作事项

3.2 创设情境，提出问题

教师：我们学过求概率的方法有什么？

学生：列举法求概率

问题1 同时掷三枚质地均匀的骰子，计算下列事件的概率：

(1)三枚骰子的点数相同

(2)三枚骰子点数的和大于或等于11

设计意图：通过复习回顾概率的基础知识，帮助学生回忆所学知识，为本节课的学习准备基础知识

问题2 列举法求概率适用范围是什么？

学生：结果有限，可能性相等的随机事件

教师：但很多时候事件发生的可能性并不均等，例如每个骰子的质量和大小都会存在误差，这使得骰子之间并不一致我觉得列举法有漏洞，那有没有更好的办法？我们不妨从这节课的知识来解析为什么会出现“十赌十输”的情况

设计意图：以旧知识的漏洞，引发疑问，引出新方法、新理论，为之后的实验验证埋下伏笔，引出模拟场景

3.3 师生讨论，设置场景

问题3 如果我连续投骰子40次，结果是“大”的次数应该为20次，你们认为对吗？

设计意图：再次混淆频率与概率的含义，引发对立矛盾，激发兴趣

学生：正确，因为“大”的概率是05

学生：不正确，40次里面不一定恰好20次“大”

教师：我们不妨做一个投骰子的实验来体验一下，看看到底谁对谁错

设置模拟投骰子：

三个骰子算总点数，总点数为3至10称作“小”，总点数11至18为“大”

学生：我昨天有预习，根据课本知识，我能做到不输钱，甚至还能赢钱！

教师：有些人正是觉得学习了概率知识，就掌握了骰子大小的规律，能做到不输甚至赢钱但他们忽视了一些因素，我们不妨从一会儿的实验结果来看看大家到底是赢钱了还是输钱了

设计意图：制定实验规则，模拟投骰子场景，让学生通过实验验证自己的猜想，让学生体会数学知识来源于生活，体会概率知识在禁赌中的价值

3.4 小组合作，实验探究

活动1 小组实验活动

活动要求 ①分组：7人为一组，共8组，其中组长1人，组员6人②分工：组长负责摇骰子和负责记录“大”“小”出现次数；组员利用道具钱币进行投注③任务：每个小组摇骰子50次，如表1所示④展示：每个小组派代表把实验数据填入电脑的Excel总表上，如表2所示

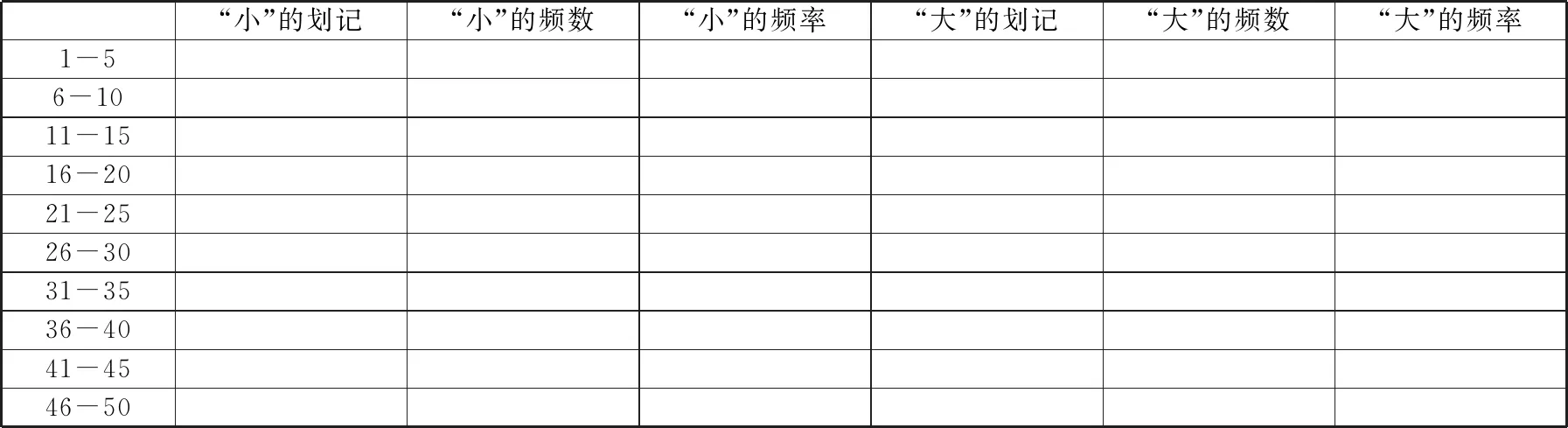
表1 学生投骰子统计表

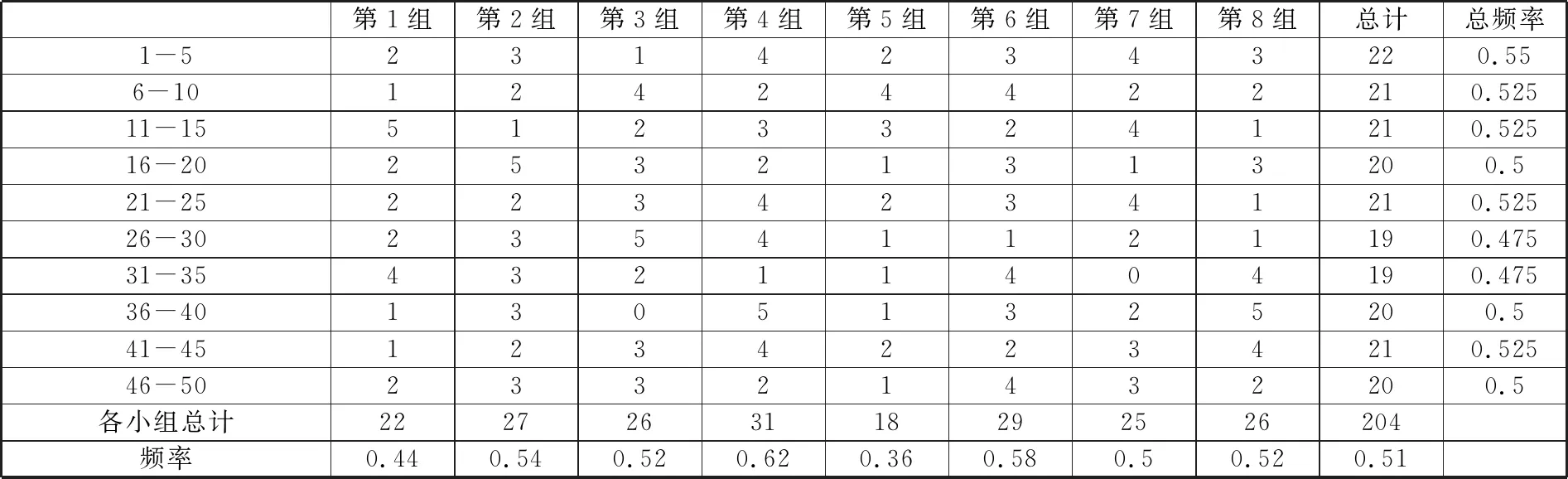
表2 投骰子出现“大”次数小组统计表

教师：同学们猜想40次的摇骰子，出现20次“大”或“小”的机会相等吗？请同学们观察上表，小组讨论一下，说说你们小组发现了什么？

学生：每个小组的结果不一样，每个小组“大”的频率不一样这可能与统计数据太少有关，我们不妨把每个小组的数据统计放一起，看看“大”的频率是多少

教师：那我们把全部小组的数据进行汇总，大家看一看

3.5 小组交流，探究发现

每个小组的实验数据汇总如表3所示

表3 投骰子出现“大”的次数与频率的总统计图

投骰子出现“大”的频率对应的折线图如图2所示

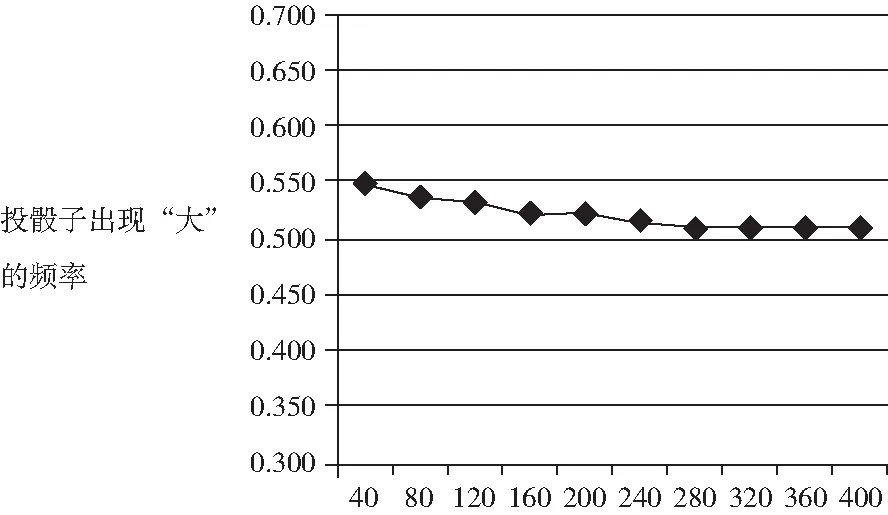
图2

活动2 分析图表，初探结论

对比各个小组的统计表和对应的折线图，分析相关图表的数据内涵

设计意图：让学生经历数据的收集，整理描述与分析的过程，进一步提高学生的统计意识，为下一步发现数据中隐藏的规律做好准备

学生：随着投骰子次数增加，出现“大”的频率逐渐向 05 靠拢出现“小”的频率也逐渐向05靠拢

3.6 师生交流，总结结论

教师：由于开始实验次数太少，得到开“大”的频率与概率可能有较大的误差，但通过学生投骰子次数的增加，频率有什么变化？

学生：频率逐渐稳定在一个数——05

得出结论：大数定律——随着大量的重复实验，一个随机事件发生的频率可以估计它的概率

3.7 模拟场景，发掘误区和赋予德育

统计学生投骰子的结果，让学生分享其中的心理变化过程

活动3 探究学生输钱的原因

学生1：之前有几次连续开“大”，我觉得下一次肯定开“小”，所以全部投注了“小”，但结果还是开“大”

教师：人们常常误以为，随机就等同于均匀过去一段时间内发生的事件不均匀，大家就会以为未来的事情会尽量向“抹平”的方向发展也就是如果连续开“大”几次的话，人们就自认为下一次开“小”的机会就会更大但大数定律工作机制，不是为了和过去已发生的事情搞平衡与对抗随机性是不受之前的结果影响的也就是说，每一次投骰子，都与之前的结果是没联系的

学生2：根据生活经验和课本的知识，我每次都投注“大”相同的金额，但还是输钱了，为什么呢？

教师：这是另一个坑——赌徒破产定理你们觉得投注了50次，开“大”的频率应该等于概率——05，这是你们对大数定律的误解，大数定律成立的条件是“大量重复”实验那具体得多少次才算“大量”，数学家给出了答案是无穷大

设计意图：通过实验情况与理论知识的矛盾，加强学生对大数定律的进一步理解，使学生认识在具体情境中运用大数定律时要注意随机性与大量性

学生3：我开始时小额投注，赢了一点，之后胆子大了，加大投注的金额，反而输钱了

学生4：我也是这种情况，想加大投注，赢回之前的本钱，但越是这样想，越输得多

教师：因为赌徒的心理一般是一赢钱，就开始变得大胆；一输钱，就想回本往往以血本无归收场

设计意图：通过分析实验情况与学生心理状况，加强学生对禁赌的进一步理解，使学生认识在具体情境中运用实验结论，探究赌博的危害，培养学生禁赌和反赌的意识

3.8 运用新知，堂上小测

活动4 学生根据刚才的知识，解决具体问题

①小新抛一枚质地均匀的硬币，连续抛三次，硬币落地都为正面朝上，如果她第四次抛硬币，那么硬币正面朝上的概率为( )

②下列说法正确的是( )

A.“明天晴天的概率是90%”表示明天有90%的时间都有太阳

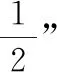
C.“彩票中奖的概率是01%”表示买1000张彩票肯定会中奖

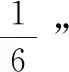
③在一个不透明的口袋中装有6个红球和若干个白球，它们除颜色外其他相同通过多次摸球试验后发现，摸到红球的频率稳定在25%附近，则口袋中白球可能有( )

A.16个 B.18个 C.20个 D.22个

④在一个不透明的盒子中装有个小球，它们只有颜色上的区别，其中有3个绿球，每次摸球前先将盒子中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复摸球试验后发现，摸到绿球的频率稳定在03，那么可以推算出大约是________

⑤某小组做“用频率估计概率”的试验时，绘出的某一结果出现的频率折线图，如图3所示，则符合这一结果的试验可能是( )

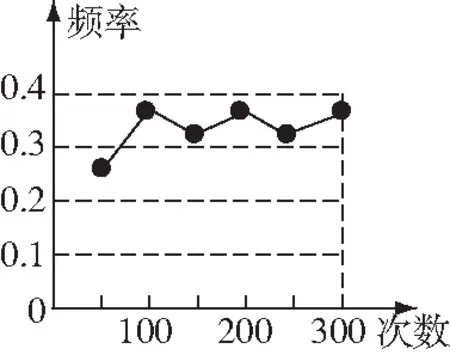
图3

A.抛一枚硬币，出现反面朝上

B.掷一个正六面体的骰子，出现4点朝上

C.一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是黑桃

D.从一个装有2个白球1个红球的袋子中任取一球，取到的是红球

⑥在一个不透明的盒子里装有黑、白两种球共60个，小颖做摸球实验，她从中随机摸出一个球记下颜色放回，不断重复上述过程，下面是实验中的一组统计数据：

摸球的次数n1003005008001000摸到白球的次数m65178302481599摸到白球的频率0.650.5930.6040.6010.599

(1)请估计：当很大时，摸到白球的频率将会接近________；(精确到01)

(2)假如你摸一次，你摸到黑球的概率(黑球)=______；

(3)试估算盒子里黑、白两种颜色的球各有多少只

思考题：鱼塘主想知道鱼塘里有多少条鱼，但又不想全部捞起来小明想到一个办法，首先捕捞30条鱼，在鱼身上做上记号然后放回池塘，接着第二天再捕捞一网，这次捕到50条鱼，其中5条鱼是有记号，则可以算出池塘中鱼的条数约为________

设计意图：培养学生用频率估计概率解决实际问题的能力

4 教学反思

在教学实验的设计中，如果教师采用课本的实验，教学课题会因为学生缺乏兴趣而变得枯燥乏味，不利于学生对实验的操作与探究，造成学生对知识理解不到位，出现文章开头的因学生理解错误而做错题的情况从这次实验活动的过程看，学生对投骰子活动非常感兴趣，自主探究，对相关知识的记忆、理解和掌握更加深刻在教学中，教师和学生共同解决各种疑问，实验探究结论，分析结论的成因，可以培养学生发现问题、实验操作、小组合作、独立思考的能力，使学生体验数学发现和探究精神和乐趣

5 结 语

初中阶段数学教材中，实验操作内容较少，有些实验过于单调和枯燥，教师可以根据生活实际对此进行调整数学实验的设计可以从趣味性、实用性、德育渗透等方面进行修改，让学生重视数学实验，认真对待实验操作环节并思考实验结论，从而培养学生的数学思维和核心素养