智慧教育云平台下“几何概型”导学案教学设计

◎易 斌 郝 圆

(桂林市第十八中学，广西 桂林 541004)

智慧教育就是把学科教学与信息技术深度融合，展现教育智慧的教育，本文按《导、学、议、评、练、悟——学案导学“六步”教学模式刍议》提出的“导、学、议、评、练、悟”六步导学模式，与同人探讨智慧教育云平台下学科教学与信息技术融合的“几何概型”的导学案教学设计

一、导

(一)目标定向

1知识目标：

(1)归纳概括几何概型的基本特征

(2)通过特例，由特殊到一般得出几何概型计算公式

(3)会解决简单的几何概型问题

2方法目标：

(1)经历探究几何概型的过程，体验由特殊到一般的数学思想方法

(2)通过解决几何概型问题，领悟合理选择测度计算几何概型的数学方法

3素养目标：

通过类比古典概型特征归纳出几何概型特征，领悟几何概型概率计算公式及解决几何概型问题等体验过程，发展学生逻辑推理、抽象概括、数学建模等数学核心素养

(二)重难定位

1重点：理解几何概型概念，灵活运用几何概型公式计算概率

2难点：发现“等可能”变化的量，并用其作为测度计算几何概型

【设计说明】(1)投影：用幻灯片逐条投影目标和重难点，学生集体朗诵，印象深刻

(2)明确：让学生明确本节课在知识、方法、素养各维度要达成的学习目标以及学习的重难点，做到有的放矢，抓住核心内容学习，突破难度

(三)新课导入

【情境导入】思考1：一根长为3的绳子，

①被其上、、、、五个点均分成六段，如图1，从、、、、中任选一点将绳子剪断，那么剪得的两段均大于1的概率是多少？

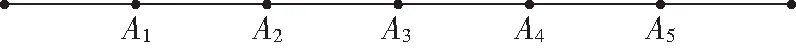
图1

②拉直绳子后剪成两段，求这两段的长度都大于1的概率

【设计说明】(1)观察思考：利用Flash动画演示绳子剪断的过程，让学生观察剪法的区别，利于学生在直观感受中思考、发现解决问题的方法

(2)温故知新：①是古典概型，用来温故，②不是古典概型，激发认知冲突，用来知新

(3)探究算法：用以下问题链导学，分析②的特征，引导学生探寻合理计算概率的新方法

【问1】试验中的基本事件是什么？

【问2】每个基本事件的发生是等可能的吗？

【问3】是古典概型吗？

【问4】如何计算其概率？

因绳子在任意位置剪断是等可能的，记事件A为：剪出两段绳长都大于1.绳子分成相等的三段，当剪断位置在中间段上时，事件A发生.

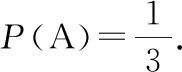
(4)感悟：在等可能前提下，

思考2：甲、乙两人玩如图乙所示两个转盘游戏，规定当指针指向N区域时，乙获胜，其余情况甲获胜，求两种情况下甲获胜的概率

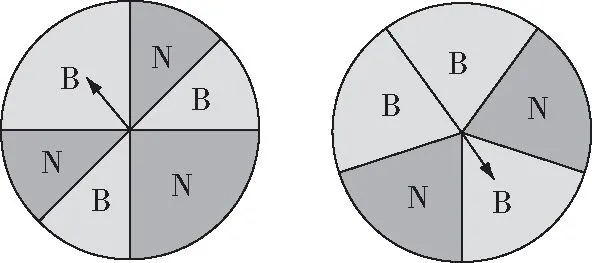
图2

【设计说明】(1)演示：动画演示转盘游戏,激发学生学习兴趣

(2)类比：类比思考1，选择用面积算概率，发展逻辑推理的素养

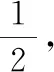
(4)感悟：在等可能前提下，

变式1：如图3，指针落在B区域的概率(B)可以用哪种量来算？

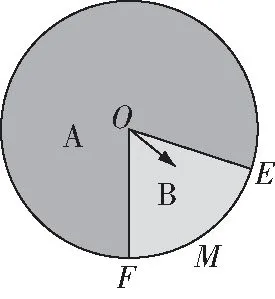
图3

【设计说明】(1)演示：动画演示指针转动过程，让学生在观察中体会哪些量在等可能变化

(3)感悟：在等可能前提下，

变式2：如图4，指针落在B区域的概率(B)可以用哪种量来算？

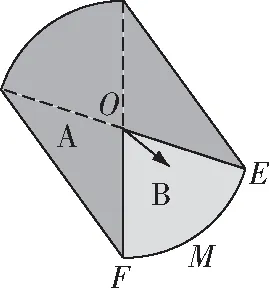
图4

【设计说明】(1)演示：动画演示指针转动过程，让学生在观察中体会哪些量在等可能变化

(2)理解“等可能”：深刻理解等可能性，体会并发现均匀变化的量，为突破教学难点埋设伏笔

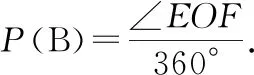
(4)感悟：恰当选择一种等可能变化的量(测度)，是准确计算概率的关键

思考3：在体积为1的正方体内含有一个质点，正方体内有一体积为02的小球，求质点在小球内的概率

【设计说明】(1)演示：用动画演示质点在正方体中随机运动，让学生在观察中体会哪个量在等可能变化

(2)探究算法：观察质点在正方体中的活动空间，发现体积在等可能变化，类比得:

(3)感悟：在等可能前提下，

二、学

【导学内容】任务1：构建几何概型概念

【问5】上述试验有什么共同特点？

【设计说明】(1)归纳共同特点：

①________________性：试验中所有可能出现的基本事件有________；

②________________性：每个基本事件出现的________________相等

(2)抽象几何概型:________________________________________

(3)发展素养：学生在合作学习中归纳共性，抽象概念，发展逻辑推理、数学抽象的核心素养

【导学内容】任务2：探究几何概型概率计算公式

【问6】如何求几何概型的概率？

【设计说明】(1)分析：由上述思考题知，在等可能前提下，可以借助长度、面积、体积、角度等的比值求概率

(2)概括公式:

(3)发展素养：学生在合作讨论中概括公式，发展逻辑推理、数学抽象的核心素养

【导学内容】任务3：几何概型概率计算公式的应用

【例2】小明在公交站台等一辆公交车，发现表停了，他记得每20分钟会有一辆公交车到达，那么他等车时间不超过8分钟的概率是多少？

【例3】在等腰直角三角形中的斜边上任取一点,求<的概率

【设计说明】(1)分析：学生独立思考或合作讨论，分析实验的全部结果构成的区域是什么，要计算的事件构成的区域是什么，试验中哪些量在等可能或均匀变化，选择哪个量作为测度来计算概率

(2)求解：学生独立解答或合作探究解答，发展学生数学建模的核心素养

三、议

1小组交流：

各小组交流导学内容的自学成果，以“兵教兵”方式解决疑惑

2代表展示：

由各小组代表汇报本组自学成果及未解决的问题

3深化讨论：

(1)学案中各小组学习的共同困惑与尚未解决的重点问题

(2)讨论【例3】的变式：过等腰直角三角形的直角顶点在∠内部作射线，与线段交于点求>的概率

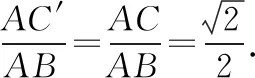
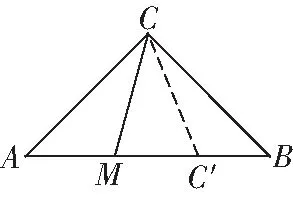
图5

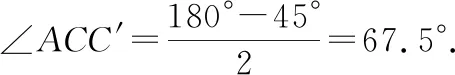
设A={在∠内部作射线与线段交于点，<}，则角度在等可能变化，选“角度”为测度

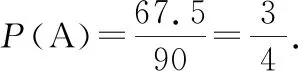
议一议：哪个解法正确？

四、评

1启发点拨：点评学生自学中普遍存在的疑难与典型问题

如【例2】学生对实验的全部结果构成的区域是什么及要计算的事件构成的区域是什么存在疑惑，教师可做如下点评：

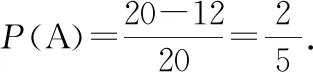
再如对【例3】的变式，学生议论后仍无法辨别哪种解法是正确的教师可做如下点评：

【例3】变式的解法1与【例3】的解法一样，都把长度作为测度，也就是试验时，“长度”是等可能或均匀变化的，不妨用Flash动画与几何画板对【例3】及其变式进行动画实验演示，学生不难发现【例3】中等可能变化的量是“长度”，【例3】的变式中均匀变化的量是“角度”，而不是“长度”，故解法2是正确的，另外，仔细读题，也不难得到与动画演示相同的结论教师由此引导学生，在计算几何概型时，一定要选“等可能或均匀”变化的量作为测度，要根据题意分析出哪个量是等可能变化的，课堂教学难点在此突破

2精讲精评:点透方法规律，举一反三

解决几何概型问题的基本步骤：

(1)用几何概型定义判定是不是几何概型

(2)选择等可能或均匀变化的量作为计算概率的测度

(3)用几何概型概率计算公式求解概率

五、练

1达标测试：

【效果检测】(1)一个铁轨交叉口的指示灯，停止灯亮的时间为40 s，危险灯亮的时间为15 s，通行灯亮的时间为50 s，当火车到路口时看到通行灯亮的概率是________

(2)一个小球在一个棱长为4的正方体形状的玻璃缸内任意运动，如果小球在运动过程中一直保持与玻璃缸6个面的距离均大于1，则称其为“安全运动”，求小球“安全运动”的概率

(3)直角三角形,其中∠=60°在斜边上任取一点,那么小于的概率有多大？

【设计说明】(1)反馈：学生独立完成后展示，反馈对三个例子的掌握情况，检测学习效果

(2)纠错：利用云平台技术统计学生每题的答题正确率，及时进行纠错

2拓展提升：

【例4】已知等腰Rt△中，∠=90°

①在线段上任取一点，求使∠<30°的概率；

②在∠内任作射线，求使∠<30°的概率

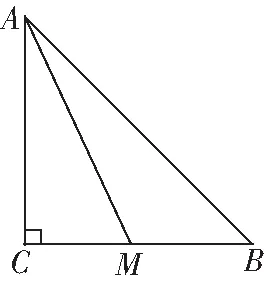
图6

【设计说明】(1)反馈：学生合作完成后展示，反馈对【例3】及其变式的掌握情况，检测学习效果

(2)提升：学生能根据问题情境，分析并发现“等可能”变化的量，合理选择测度求解概率

六、悟

师生共同进行课堂小结，梳理核心知识，感悟数学方法，形成能力

1几何概型特征：①_____________________________

；

②___________________________

2几何概型的概率公式:(A)=____________________________