参照法将任意角转化为锐角的再研究及其应用
2022-10-23 07:18龙成芳
高中数理化 2022年17期
龙成芳
(贵州省天柱民族中学)

1 问题的发现
1.1 以x 轴作为参照的重述


1.2 问题的发现

2 引入以y 轴为参照
为了解决以上问题,考虑在以x轴作为参照的基础之上,引入以y轴为参照的情况.
2.1 三角函数定义及其理解
设任意角α的终边与单位圆的交点为P(x,y),任意角α的终边与y轴的夹角为β,其中角β为锐角,根据任意角的三角函数的定义,则正弦函数为sinα=y.
(1)当角α为第一象限角时,sinα=y=cosβ,如图1所示.
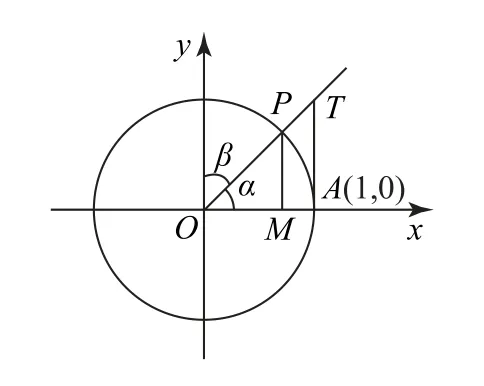
图1
(2)当角α为第二象限角时,sinα=y=cosβ,如图2所示.
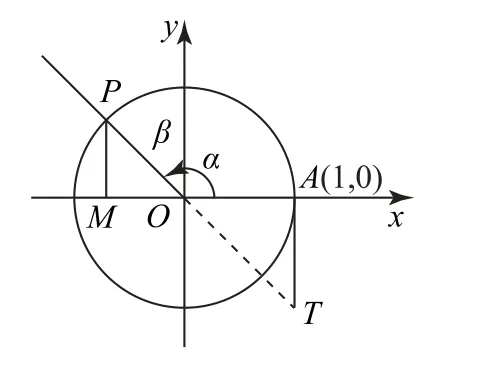
图2
(3)当角α为第三象限角时,sinα=y=-cosβ,如图3所示.
(4)当角α为第四象限角时,sinα=y=-cosβ,如图4所示.
根据三角函数的定义和前面提出以x轴作为参照情况,以上是以y轴为参照的正弦函数情况,余弦和正切的情况也是类似的.
2.2 以y 轴为参照时象限角的判定



2.3 以y 轴为参照时角的转化

若任意角的终边分别与平面直角坐标系的x轴和y轴作为参照,统一称为参照法,则只需要以x轴作为参照,计算特殊角的三角函数值,一步就可以得出结果.当需要改变三角函数名时,采用以y轴作为参照进行解题.两者相辅相成,形成一个完整的思想方法体系.
3 参照法的应用
通过以上的补充完善,参照法得到了一个全面的系统,用起来也比较直接,也不需要记公式,下面具体看看实际应用情况.
3.1 计算非锐角特殊角的三角函数值



3.2 化简求值

(2)973°=5×180°+73°,所以角973°是第三象限角.1423°=8×180°-17°,所以1423°为第四象限角.所以
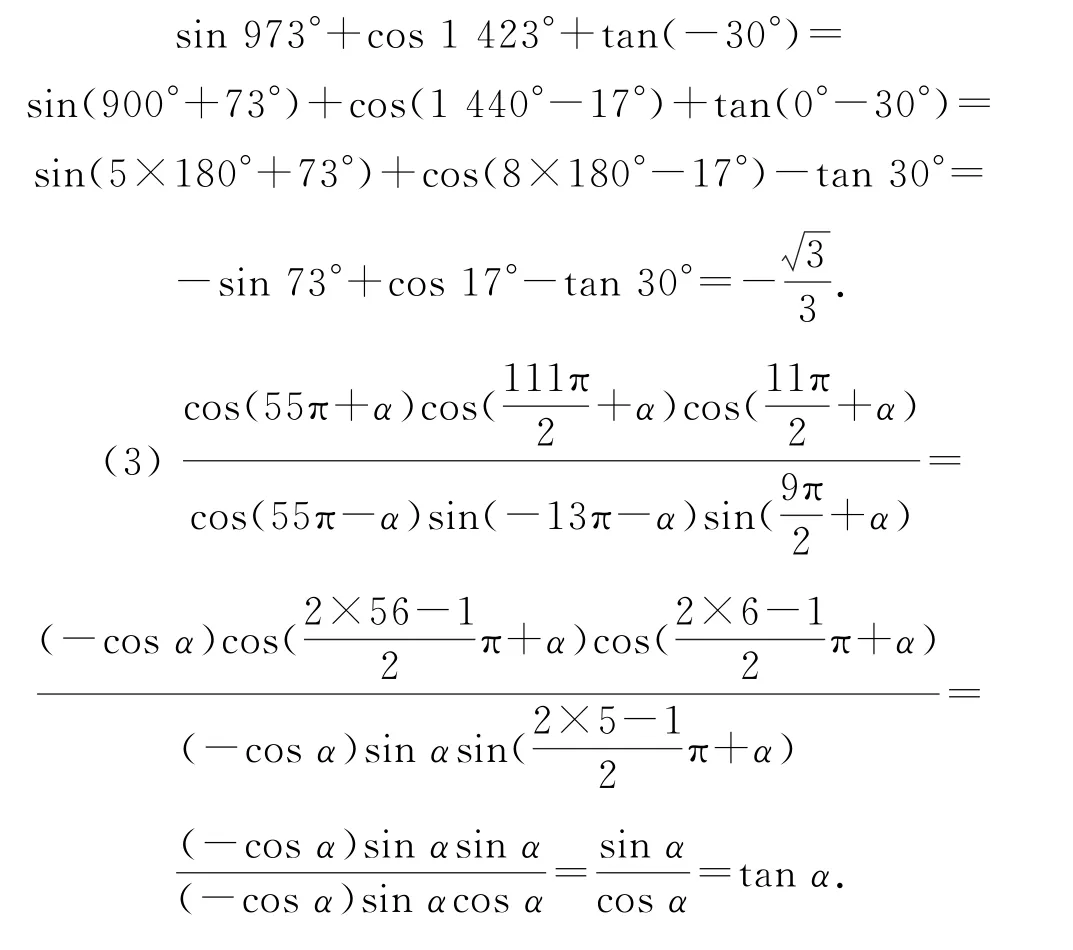
猜你喜欢
新高考·高三数学(2022年3期)2022-04-28
中学生数理化(高中版.高考数学)(2022年1期)2022-04-26
中学课程辅导·高考版(2019年4期)2019-04-25
数学大王·中高年级(2019年2期)2019-01-23
理科考试研究·高中(2017年7期)2017-11-04
中学生天地(B版)(2016年12期)2017-01-05
中学生数理化·高二版(2016年9期)2016-05-14
中学生数理化·八年级数学人教版(2016年1期)2016-03-16
数学大世界·小学低年级辅导版(2010年9期)2010-09-08
小学教学参考(数学)(2009年12期)2009-05-31

