平面向量问题分类讨论例析

朱子琨

(甘肃省天水市第十中学)

对于平面向量问题,由于它具有“数”与“形”的双重特性,求解时往往需要对原问题进行分类讨论,以达到完整解决问题的目的,这就是数学解题中最常用的分类讨论思想.下文结合具体实例探讨平面向量问题中的分类源自哪里,谈谈分类讨论思想在解平面向量问题中的应用,供读者参考.

1 因向量的方向不确定分类讨论

解题时需要讨论向量是否共线,同时,当已知两个向量平行或共线时,往往需讨论它们的方向是同向还是反向,否则解答过程不严密、也不完整,容易丢分.

例1 求证:

|a＋b|2＋|a-b|2＝2(|a|2＋|b|2).

分析 在本题中,向量a与b可能共线,也可能不共线,所以解题时应分别加以讨论.

证明 若向量a,b共线.

当向量a,b共线且方向相同时,则

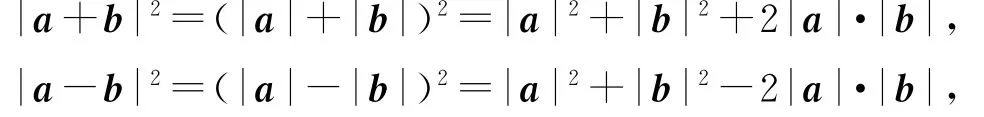
所以|a＋b|2＋|a-b|2＝2(|a|2＋|b|2).

当向量a,b共线且方向相反时,则

所以|a＋b|2＋|a-b|2＝2(|a|2＋|b|2).

若向量a,b不共线,如图1所示.

图1

解答本题容易犯的错误就是“顾此失彼”,从而导致证明不严密.对于平面向量证明题,一般可采取数形结合的方法,以确保讨论问题的完整性.

在求有向线段分点坐标时,不必过分强调公式记忆,可以转化为向量问题后解方程组求解,同时应注意分类讨论.

2 因向量的位置关系不确定分类讨论

平面向量既有大小又有方向,它的起点与方向确定了它的位置.对于某些平面向量中的定性问题,当向量位置不确定时需分类讨论.

例3 已知向量a,b,则对于向量c,若满足a＋b＋c＝0,那么能说明表示a,b,c的有向线段构成三角形吗?

分析 题中没有告诉我们向量a与b是否平行,此外这两个向量也有可能是零向量,故需要分3种情形加以讨论.

解 如果向量a与b中至少有一个向量是零向量,那么它们无法构成三角形;

如果a与b平行,那么无论它们是同向还是反向,都无法构成三角形;

图2

判断几个向量能否构成几何图形,既要考虑向量的方向,又要看向量的模长,满足时可以直观画出满足条件的几何图形.解答这类问题时应考虑特殊情形,否则极易造成漏解或解题不严密的现象.

3 因参数不确定分类讨论

当平面向量的题目中含有参数时,由于参数的范围没有确定,所以也需要分类讨论.这类问题往往以向量运算为途径,最终转化为含参函数问题,尤其是转化为二次函数含参问题.

分析 先根据条件求出a·b及|a＋b|,把它们代入f(x)得到以cosx为自变量,且含有参数λ的函数f(x).由函数解析式知,要求该函数的最小值,必须要对参数λ进行分类讨论.

解 (1)由已知条件可得2cosx.

(2)f(x)＝cos2x-4λcosx＝2(cosx-λ)2-1-2λ2.

当λ＜0 时,当且仅当cosx＝0 时,fmin(x)＝-1,与已知矛盾.

对于含有参数问题,必须注意取不同的参数值是否产生不同的结果,解答时要有分类讨论的意识.

总之,分类讨论的思想是数学解题常见的重要思想.应用这种思想的关键是对需解决的问题进行正确分类,分类要坚持科学合理、互斥、无漏和最简的原则,保证分类的科学性与有效性.对于平面向量问题来说,分类讨论归根到底是由向量的方向与大小的不确定性引起的,当含有参数时,还要关注参数是否需要分类讨论.

链接练习