装配误差和齿面修形对曲线圆柱齿轮传动误差的影响

张学刚 谢永春 王鹏飞

（攀枝花学院 智能制造学院， 四川 攀枝花 617000）

0 引言

根据啮合时的接触形式不同，曲线圆柱齿轮可分为点接触和线接触[1-2]。 相对于线接触曲线齿轮，点接触曲线齿轮对装配误差不敏感，在装配误差作用下不易出现轮齿边缘接触，某些情况下其传动平稳性比线接触齿轮更强。点接触曲线齿轮是一种平行轴齿轮，其齿形呈现弧形。与直齿轮、斜齿轮和人字齿轮相比，这种齿轮加工效率较低，成本较高，在传动系统中应用较少[3-4]。由于其齿形为弧形，在传动过程中，轴向窜动力可相互抵消，且具有更好的润滑性能[5]。目前，不少国内外学者开展了对曲线圆柱齿轮传动性能的研究，以争取克服齿轮传动过程中的问题。

Tseng 等先后分别研究了采用盘形面铣刀加工[6-7]和滚齿加工[8-9]所得曲线圆柱齿轮的数学模型、根切现象、无载荷传动误差等。Wu 等[10-12]采用圆弧曲线对曲线圆柱齿轮齿面进行修形，并探讨了修形参数和刀盘半径对齿轮的无载荷和有载荷传动误差的影响。苏进展等[13]推导了带抛物线修形的曲线圆柱齿轮的齿面方程，并研究了某种修形系数下，三类装配误差对无载荷传动误差的影响；在此基础上，还研究了某种装配误差下抛物线修形系数对无载荷传动误差的影响[14]；此外，还通过预设4阶无载荷传动误差，对曲线圆柱齿轮齿面进行了优化设计[15]。Fuentes 等[16]330-339研究了刀盘半径对曲线圆柱齿轮的齿面接触应力和齿根接触应力的影响，以及利用齿顶修形消除齿顶接触应力；此外，还对比研究了曲线圆柱齿轮与直齿轮和斜齿轮之间的力学性能。马登秋等[17]基于分心理论研究了曲线圆柱齿轮的接触应力问题。Sun 等[18]研究了齿宽和刀盘半径对曲线齿轮接触应力的影响。侯力等分析了曲线齿轮的振动特性[19]、齿面曲率特性[20]、几何特性[21]以及润滑性能[22]等。

传动误差是评价齿轮在传动过程中产生噪声和振动的重要指标之一，其中，传动误差分为无载荷传动误差和载荷传动误差。无载荷传动误差仅研究齿轮副在无载荷条件下的传动误差，而齿轮副在实际工作中是存在载荷的。因此，对曲线齿轮载荷传动误差的研究更符合实际情况。然而，现有文献尚未涉及到对曲线齿轮载荷传动误差的研究。本文中利用有限元法，并充分考虑点接触曲线圆柱齿轮在实际装配过程中的误差，研究了齿面抛物线修形对点接触曲线齿轮载荷传动误差的影响。

1 齿面数学模型

齿面数学模型是轮齿接触分析（TCA）、无载荷传动误差分析以及建立有限元模型的基础。曲线齿轮传动副中，对其中一个齿轮的齿面进行抛物线修形可得到抛物线传动误差曲线，提高齿轮传动平稳性、降低振动和噪声水平。关于未修形齿轮齿面的数学模型不再赘述，可参见文献[16]322-329。本文中只对修形的齿面方程进行推导。

1.1 齿轮成型原理

曲线圆柱齿轮副一般采用格里森双刃面铣式刀盘对其进行铣削加工，如图1 所示。图1 中，Rc为刀盘曲率半径；z为待加工齿轮的齿数；rp为待加工齿轮的分度圆直径。

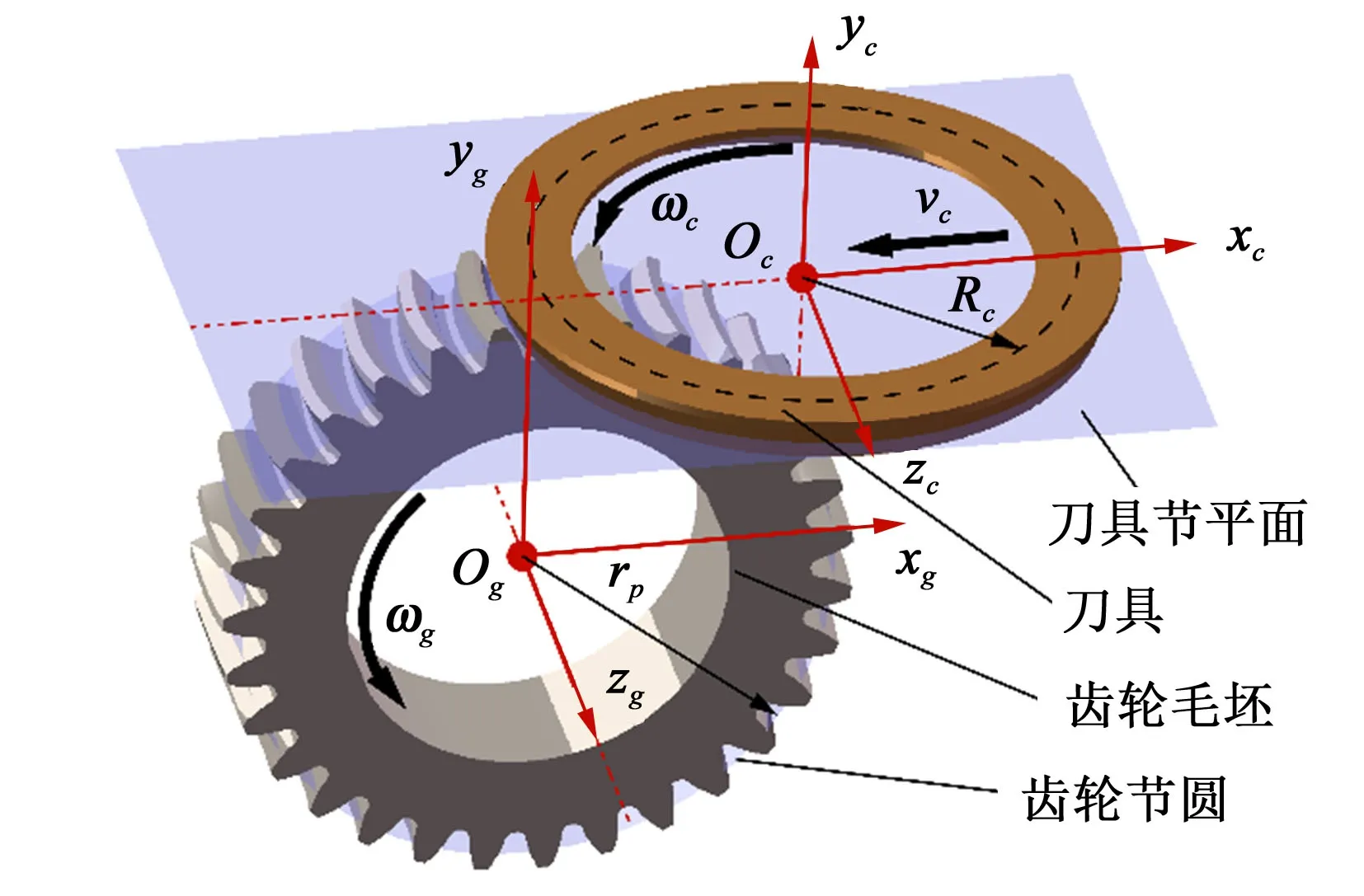
图1 曲线圆柱齿轮的加工示意图Fig.1 Schematic diagram of processing curvilinear cylindrical gears

加工齿轮时，高速旋转的刀盘节平面与待加工齿轮的节圆柱表面相切，刀盘沿xc轴方向以速度vc往复移动，齿轮毛坯以角速度ωg绕zg轴顺/逆时针旋转，刀盘的移动速度和齿轮毛坯的旋转速度满足vc=rpωg。当1个齿槽加工完毕，刀头从齿槽中分离，齿轮毛坯转动1个分度360（°）/z，齿轮和刀盘继续重复上一步的展成运动，直到齿轮的所有齿加工完成。

1.2 修形齿面数学模型

齿面修形可以改变齿面的几何形态。未修形齿轮在啮合过程中易出现线性传动误差，相邻两啮合周期之间的传动误差线存在阶跃效应，会造成较大的振动和噪声。若对齿面进行齿廓抛物线修形，其传动误差曲线为抛物线，相邻两啮合周期之间的抛物线存在交叉，这将会消除线性误差曲线中存在的阶跃效应，从而减小或消除啮合过程中的振动和噪声[23]。这种修形方法也是在弧齿锥齿轮齿轮设计中为了减小振动和噪声的一种常见手段。

图2 所示为刀盘上的抛物线修形刀头截面示意图。图2中，a为齿顶高系数；b为齿根高系数；ρ为刀尖过渡圆角系数；αn为压力角；m为模数；u为主切削刃长度的变量；λ为过渡圆角的角度变量；Δytp为修形抛物线的偏置距离刀。盘曲率半径Rc为刀头中心线与刀盘旋转中心之间的距离；坐标系Sc（Ocxcyczc）固定于刀盘的旋转轴线与节平面的交点处，与图1 中对应。刀头左侧的外刃用于加工齿轮的凹齿面；刀头右侧的内刃用于加工齿轮的凸齿面。

图2 刀头截面示意图Fig.2 Schematic diagram of the cross-section of the cutter head

将刀头的内刃和外刃抛物线部分表达在坐标系Sib中，表示矢量形式为

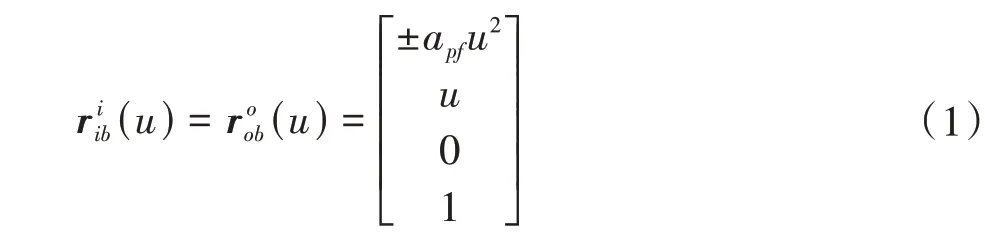
式中，上标i为内刃计算符号；o为外刃计算符号。全文公式均按此规定进行标注。

将刀头切削刃部分转换到坐标系Sb中，表示为

接下来，将刀头切削刃部分转换到坐标系Sc中，表示为

式中，当上标g=i时，表示内刃；当上标g=o时，表示外刃；u、θ均为形成齿轮产形面的几何参数。

将齿轮产形面表达在齿轮毛坯坐标系Sg中，为

式中，ψ为展成加工齿轮过程中，齿轮毛坯的旋转角度。坐标系Sc到Sg的坐标变换矩阵为

其中，

Xt=rp(sinψ-ψcosψ) +Rccosψ；

Yt=rp(cosψ+ψsinψ) -Rcsinψ。

根据微分几何和啮合原理[23]，采用工程解法可求解出曲线齿轮的啮合方程，表示为

将式（5）代入式（4）中，可求出齿面关于u和θ的双参数数学模型。若给定一组u、θ的值，则可求解出齿面上的一个点。根据文献[24]中的方法可求解出齿面上一系列规则分布的点云数据，这些点云数据可为后续齿轮参数化有限元模型的建立奠定基础。

关于齿根过渡曲面方程的推导和抛物线修形部分齿面类似，这里不做过多说明。

2 装配误差下初始接触的定义

装配误差在齿轮副实际装配过程中是不可避免的，它将会引起工作中的齿轮副接触状态以及传动误差发生改变。图3所示为齿轮副装配误差坐标系的定义。假设小轮安装于坐标系S1上，大齿轮安装于坐标系S2上，它们的旋转中心与自身的Z轴重合。图3中，坐标系Sf为全局坐标系；Sk、Sl、Sm、Sn分别为定义4类装配误差（ΔC、ΔA、ΔH、ΔV）的辅助坐标系。其中，ΔC表示中心距误差；ΔA表示轴向误差；ΔH表示轴扭转误差；ΔV表示轴交错误差。ϕp、ϕg分别表示齿轮副啮合过程中小齿轮和大齿轮的转角。

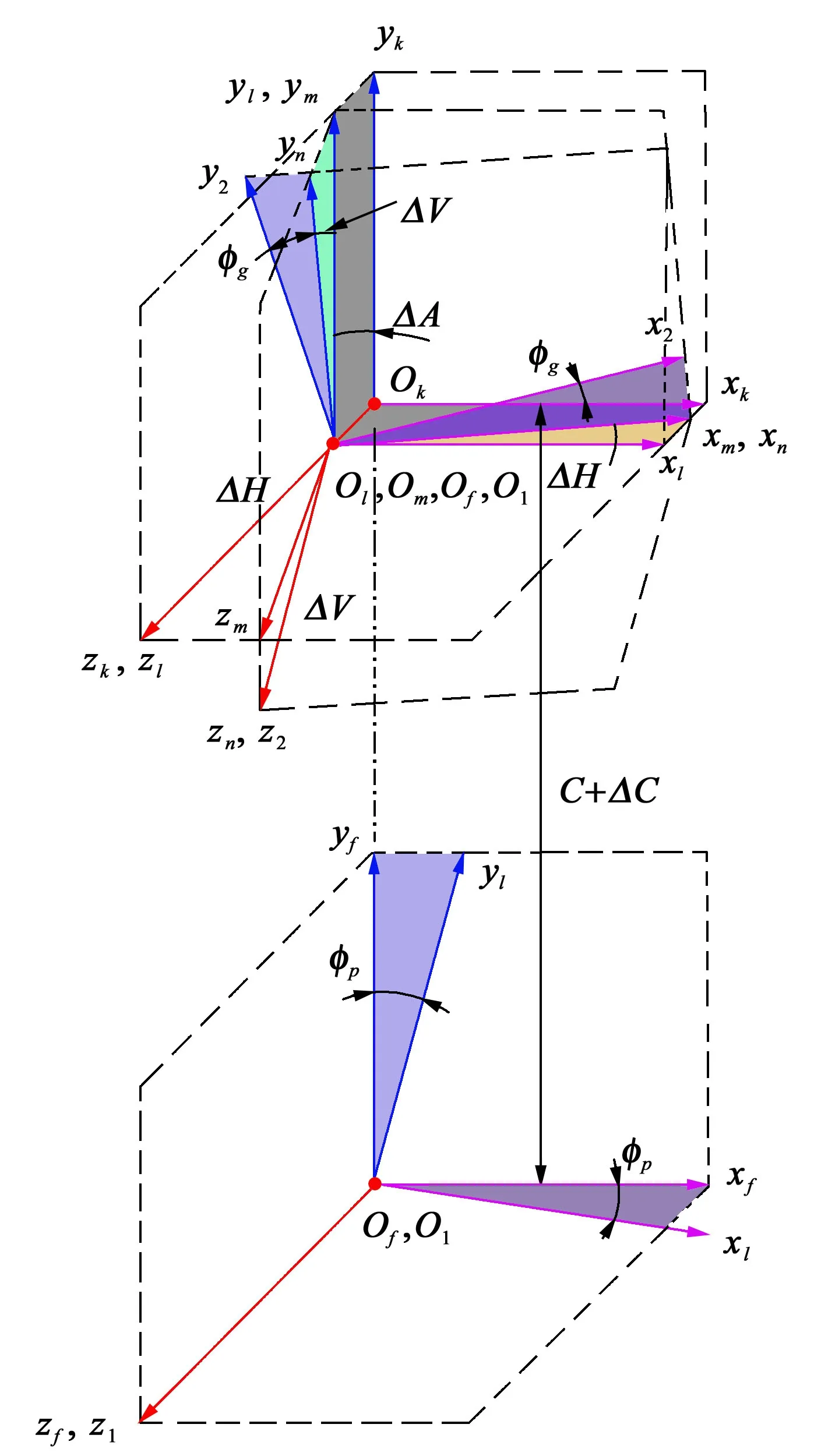
图3 齿轮副装配误差坐标系定义Fig.3 Definition of coordinate systems of the gear pair assembly errors

为了使齿轮副的有限元模型精准接触，需要编程计算两啮合齿面在无载荷条件下的初始接触位置，计算时必须将小齿轮的凹齿面和大齿轮的凸齿面转换到全局坐标系Sf中。小齿轮的凹齿面转换到坐标系Sf中，表示为

式中，up、θp与第1 节中的u和θ对应；下标p表示小齿轮；矩阵Mf，1表示坐标系S1到Sf的变换。

大齿轮的凸齿面转换到坐标系Sf中，表示为

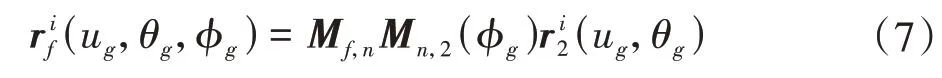
式中，ug、θg与第1 节中的u和θ对应；下标g表示大齿轮；矩阵Mn，z表示坐标系S2到Sn的变换，表示为

矩阵Mf，n表示坐标系Sn到Sf的变换，表示为

式中，

求解两啮合齿面的初始接触点，其几何意义是接触点处两齿面的位置矢量相等，且单位法向量也相等，表示为

式（9）中有6 个未知参数，5 个独立方程；若给定小齿轮转角ϕp，可以求解出其余5个参数；将求解结果再次代入式（6）和式（7）中，便可求解出两啮合齿面刚好接触时的齿面方程。

3 齿轮副有限元模型

由于曲线齿轮齿面是复杂曲面，采用商用有限元软件在三维模型上直接划分网格，所得齿面节点误差较大，将会导致齿面分析结果误差增大，甚至得到错误的结论，与实际情况严重不符[25]；而手动划分网格工作量巨大，不适合建立本文中所需的几十组有限元齿轮副模型。因此，本文中基于齿面方程所生成的规则齿面点云，将齿面点云作为轮齿有限元模型的节点数据，通过填充齿面内部节点的方式构建整个齿轮的有限元模型。采用这种方法所构建的齿轮有限元模型不存在精度损失，可以得到更准确的分析结果；而且可以通过参数化的方式批量生成所有工况条件下的齿轮副有限元模型[26]。

为了节省有限元求解时间，如图4所示，采用了5 齿有限元模型，每个齿轮模型有81 590 个节点，67 200 个六面体1 阶单元。图4 中，齿轮内圈和边界分别与自身的旋转中心刚性连接，在大齿轮的旋转中心RP-2处施加阻力矩T，小齿轮旋转中心RP-1固定。小齿轮的凹齿面为接触主动面，大齿轮的凸齿面为从动面，分析求解时，在Abaqus求解器中完成。当初始接触位置分析完成后，齿轮副的接触已稳定，小齿轮转动一个角度ϕp，开始第1 个接触位置的分析；此时，可得到大齿轮在载荷下的实际转角ϕg，齿轮在载荷下的传动误差就是大齿轮实际转角与理论转角的偏差，表达为

图4 齿轮副的5齿有限元模型Fig.4 Five-tooth finite element model of the gear pair

当第1个接触位置分析完成，小齿轮再转动一个角度，继续第2个接触位置的求解，直到所有接触位置求解完成。本文中只分析了两个啮合周期内的载荷传动误差，即，小齿轮的转角ϕp在[0，2π/zp]之内，在这两个周期的转角范围内划分了21个接触位置。

4 算例分析

本文中以表1 所示齿轮基本参数作为分析的依据，分别研究了齿轮的4类装配误差、修形量、刀盘曲率半径、修形曲线偏置量对齿轮载荷传动误差的影响。

表1 齿轮基本参数Tab.1 Basic parameters of the gear pair

4.1 装配误差对传动误差的影响

假设加工曲线齿轮所有刀盘曲率半径Rc=40 mm，修形抛物线系数apf=0.001 5，修形抛物线偏置距离Δytp=0 mm；4类装配误差参数如表2所示。每一类分为4种工况，其中，误差值0表示无装配误差。总共需完成13种工况的有限元分析。

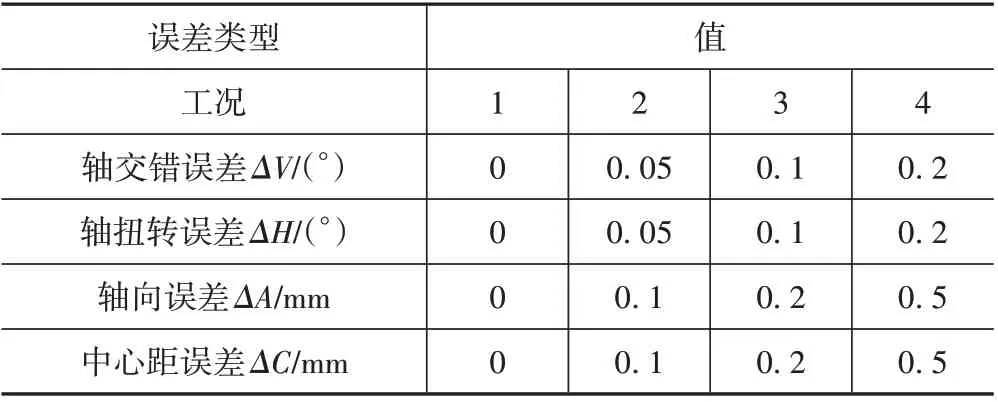
表2 4类装配误差参数Tab.2 Four types of assembly error parameters

4 类装配误差下的载荷传动误差如图5 所示。图5 中的图例“VHAC=0”表示无误差的理想装配。从图5 中不难看出，在任意装配误差下，齿轮传动误差波动明显小于理想装配，在传动过程中可起到降噪、减振的作用。此外，装配误差的值对传动误差影响较小。

图5 4类装配误差对传动误差的影响Fig.5 Influence of four types of assembly errors on transmission errors

4.2 修形量对传动误差的影响

由于第4.1节中的研究发现装配误差类型和数值对载荷传动误差影响较小，后续将不再考虑多种装配误差的影响，只考虑单一装配误差。假设齿轮副的轴扭转误差ΔH=0.2°，刀盘曲率半径Rc=40 mm，修形抛物线偏置距离Δytp=0 mm，修形抛物线系数如表3所示。表3中，修形系数越大，修形量越大。

表3 修形抛物线系数apfTab.3 Modified parabolic coefficient apf

修形量对传动误差的影响如图6 所示。结果表明，修性量越大，载荷传动误差波动越小；无修型的曲线齿轮载荷传动误差最大。

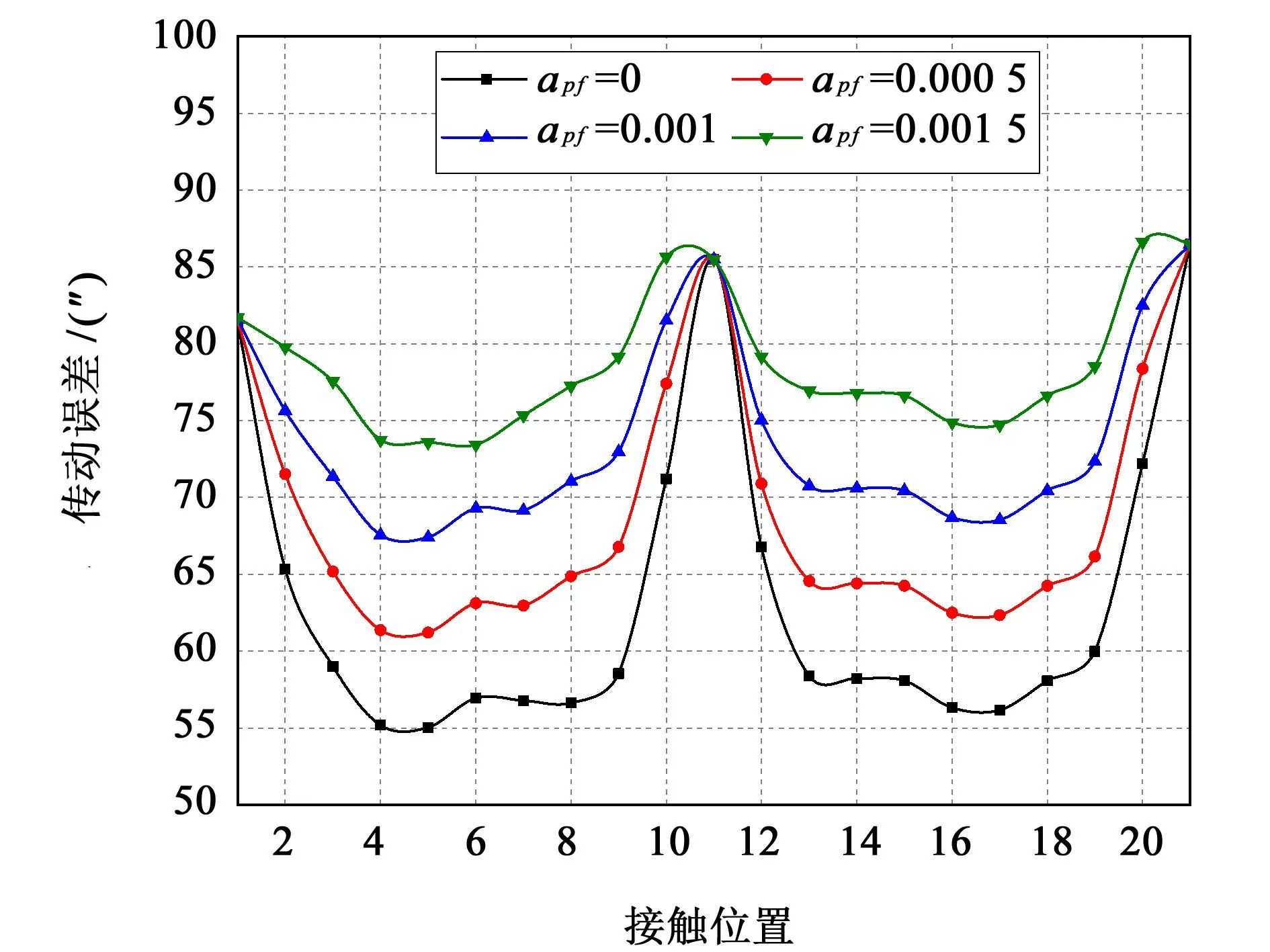
图6 修型量对传动误差的影响Fig.6 Influence of the modification amount on transmission errors

4.3 刀盘曲率半径对传动误差的影响

假设齿轮副轴向误差ΔA=0.2 mm，修形抛物线系数apf=0.001 5，修形抛物线偏置距离Δytp=0 mm，刀盘曲率半径如表4所示。

表4 刀盘曲率半径RcTab.4 Curvature radius of cutter Rcmm

刀盘曲率半径对传动误差的影响如图7所示。结果表明，随着刀盘曲率半径的增大，载荷传动误差减小，误差波动也随之减小。

图7 刀盘曲率半径对传动误差的影响Fig.7 Influence of the curvature radius of the cutter on transmission errors

4.4 修形曲线偏置对传动误差的影响

假设在理想装配条件下，刀盘曲率半径Rc=40 mm，修形抛物线系数apf=0.000 5。修型抛物线偏置量如表5所示。

表5 修形抛物线偏置量ΔytpTab.5 Offset of the modified parabola Δytpmm

修形曲线偏置对传动误差的影响如图8所示。结果表明，修型曲线相对刀盘节平面的距离越远，传动误差的波动略微增大；无偏置时，传动误差波动最小。

图8 修形曲线偏置量对传动误差的影响Fig.8 Influence of the offset of the modified curve on transmission errors

5 结论

通过对曲线圆柱齿轮载荷传动误差的研究，得出以下结论：

（1）装配误差有利于降低载荷传动误差的波动幅度，从而起到降噪和减振的效果；无误差的理想装配反而会引起较大的传动误差波动，说明修形的点接触曲线圆柱齿轮更适合工业应用。

（2）适当增加齿面修形量，其载荷传动误差波动将越小，有利于提升曲线齿轮的传动性能。

（3）随着加工曲线齿轮的刀盘曲率半径增大，载荷传动误差和误差波动都将会减小；说明加工曲线齿轮的刀盘曲率半径不宜过小，否则将会影响传动性能。

（4）齿面修形曲线的偏置对载荷传动误差的影响较小。

总的来说，采用较大曲率半径的修形刀盘所加工出的曲线圆柱齿轮传动性能更好。