基于LMD排列熵和BP神经网络的行星齿轮箱故障诊断方法
高素杰 巫世晶 周建华 郑 攀 陈 奔 许家才
(1 武汉大学 动力与机械学院, 湖北 武汉 430072)
(2 国能云南新能源有限公司, 云南 昆明 650214)
0 引言
行星齿轮箱具有结构紧凑、传动效率高、承载能力强等优势,被广泛应用于航空航天、风力发电、冶金等领域[1]。由于行星齿轮箱通常工作在恶劣的环境条件下,其太阳轮、行星轮以及内齿圈等关键部位很容易发生点蚀、裂纹、断齿等故障,若故障不能被及时发现,将影响系统正常运转,诱发严重事故[2]。因此,准确、可靠诊断行星齿轮箱故障对提升其服役性能有重要意义。
齿轮出现故障时,往往会产生非平稳、非线性振动信号[3],由于实际采集到的振动信号中通常含有较多频率成分,噪声干扰较大,传统时域分析方法,如偏度、峭度等,抗噪能力差,分析效果不够理想[4]。近年来,时频域分析和熵值特征分析被广泛用于齿轮箱故障特征提取。张海潮等[5]提出了一种基于EMD 和Hilbert 谱的齿轮箱故障诊断方法,相较于小波变换,能更精确地体现故障特征。王涛[6]提出了一种基于EEMD 和FWT 的集成方法,可有效降低信号噪声,提高信噪比。董治麟等[7]提出了一种时移多尺度排列熵(TSMPE)与极限学习机结合的滚动轴承故障诊断方法。程军圣等[8]将LMD 和时域分析提取到的特征应用于轴承故障诊断。何雷等[9]提出了一种噪声辅助LMD 与时域分析结合的方法,并应用于变速箱齿轮和轴承的故障诊断。Sharma S等[10]提出了一种基于柔性小波与排列熵集成的故障诊断方法。蒋玲莉等[11]采用基于CEEMDAN 排列熵与SVM 集成的方法,对弧齿锥齿轮3 种不同程度断齿状态进行了识别。上述方法在故障诊断领域取得了一定的进展,但并未涉及齿轮复合故障,且存在诊断成功率不够高等问题,有待改进。
针对这些问题,本文中提出一种基于LMD 排列熵和BP 神经网络相结合的齿轮箱故障诊断方法。首先,采用LMD方法对多种工况的振动信号进行分解,得到重要的PF 分量并计算排列熵值作为特征向量;然后,将特征向量输入训练好的神经网络,实现较好的故障诊断效果。
1 信号特征提取与故障诊断方法
1.1 局部均值分解
局部均值分解(Local mean decomposition,LMD)的思想类似于经验模态分解(EMD)[12],其实质是将复杂信号自适应地分解为一系列乘积分量(Product fuction,PF)和一个残余分量。对于任意一个信号x(t),LMD的具体分解流程为[13]:
(1)找到原始信号x(t)的所有局部极值点ni,并计算相邻两极值点的均值mi,即

用直线连接所有mi,并利用滑动平均方法处理后,得到局部均值函数m11(t)。
(2) 根据相邻两局部极值点求得包络估计值ai,即

用直线连接所有ai,并利用滑动平均的方法处理后,得到包络估计函数a11(t)。
(3)用原始信号x(t)减去局部均值函数m11(t),得到一个新的信号h11(t),即

(4)对步骤(3)得到的信号h11(t)进行解调,得到s11(t),即

如果a12(t)=1,则说明s11(t)为纯调频函数;否则以s11(t)为原始数据,重复迭代步骤(1)~步骤(4),直到得到纯调频函数s1n(t)为止,也即a1(n+1)(t)=1。因此,有

式中,

(5)将迭代过程产生的所有包络估计函数相乘,即可得到第1个乘积分量(FP1)的包络信号a1(t),即

(6)将包络信号与纯调频信号相乘,得到原始信号x(t)的第1个乘积分量FP1,即

(7)用原始信号x(t)减去FP1,得到一个新的信号u1(t),并以u1(t)为原始数据,重复步骤(1)~步骤(7),如此循环k次,当uk(t)为一个单调函数时,分解结束。
至此,原始信号x(t)经过LMD 分解为k个PF 分量和一个残余分量之和,即
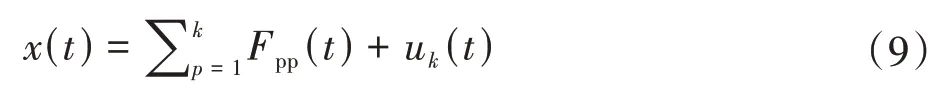
乘积分量(PF)由包络信号和纯调频信号相乘得到,具有明确的物理意义。分解得到的各PF 分量能够反映出原始信号x(t)所包含的不同成分。因此,LMD是一种很好的自适应分解方法。
1.2 排列熵
排列熵[14](PE)是一种能够衡量一维时域信号复杂程度的熵值计算方法,具有抗噪能力强、对信号突变的敏感性强[15-16]、计算效率高等优点,近年来被广泛应用于齿轮箱故障诊断中。对于一维时域信号x(t),PE的具体计算方法如下:
对原始序列X={x1,x2,…,xN}进行相空间重构。假设嵌入维数为m,延时为τ,得到重构矩阵Z为

式中,
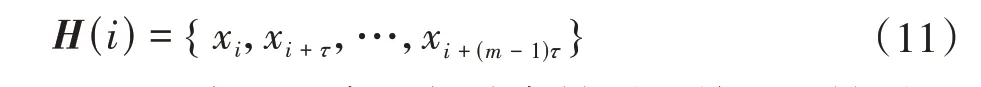
对H(i)中的元素进行升序排列,并记录排列后每个元素的位置。若同一组元素中有相等的两个值,则按照原来顺序的大小排列。对于m维重构相空间,每一组H(i)共有m!种排序可能性。统计每一种排序出现的次数,并计算它们的概率P1、P2、…、Pq,有

根据Shannon熵的定义式,得到排列熵为
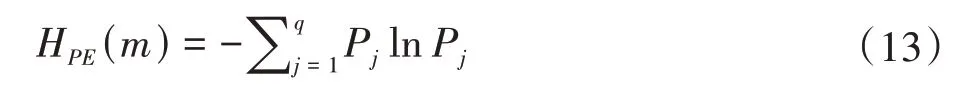
在实际应用中,常需要将排列熵进行归一化处理,即

当Pj= 1/m!时,HPE(m)能够得到最大值ln(m!),此时,HNPE(m) = 1。排列熵值越大,时间序列的无序性越强;反之,排列熵值越小,时间序列越有序。
当齿轮箱出现故障时,采集到的振动信号与正常状态下的PE 值有一定区别,且不同故障振动信号的PE 值不同。因此,可以利用PE 值作为指标,对齿轮的故障状态进行分类。但如果仅从单一尺度的排列熵值去分析故障特征,则会造成重要信息的流失。本文中将LMD与PE结合,从多个尺度分析故障特征。文献[17]中给出了嵌入维数m和延时τ的选取方法,本文中取m= 6、τ= 1。
1.3 BP神经网络
BP 神经网络是一种前馈神经网络,由输入层、中间层(隐层)和输出层组成,中间层数可以为单层或多层。网络训练采用误差逆传播方法调整各节点间的权值和阈值,当给定输入向量时,使输出向量逼近预期值,进而建立输入向量与输出向量间的非线性映射关系。BP神经网络模型如图1所示。
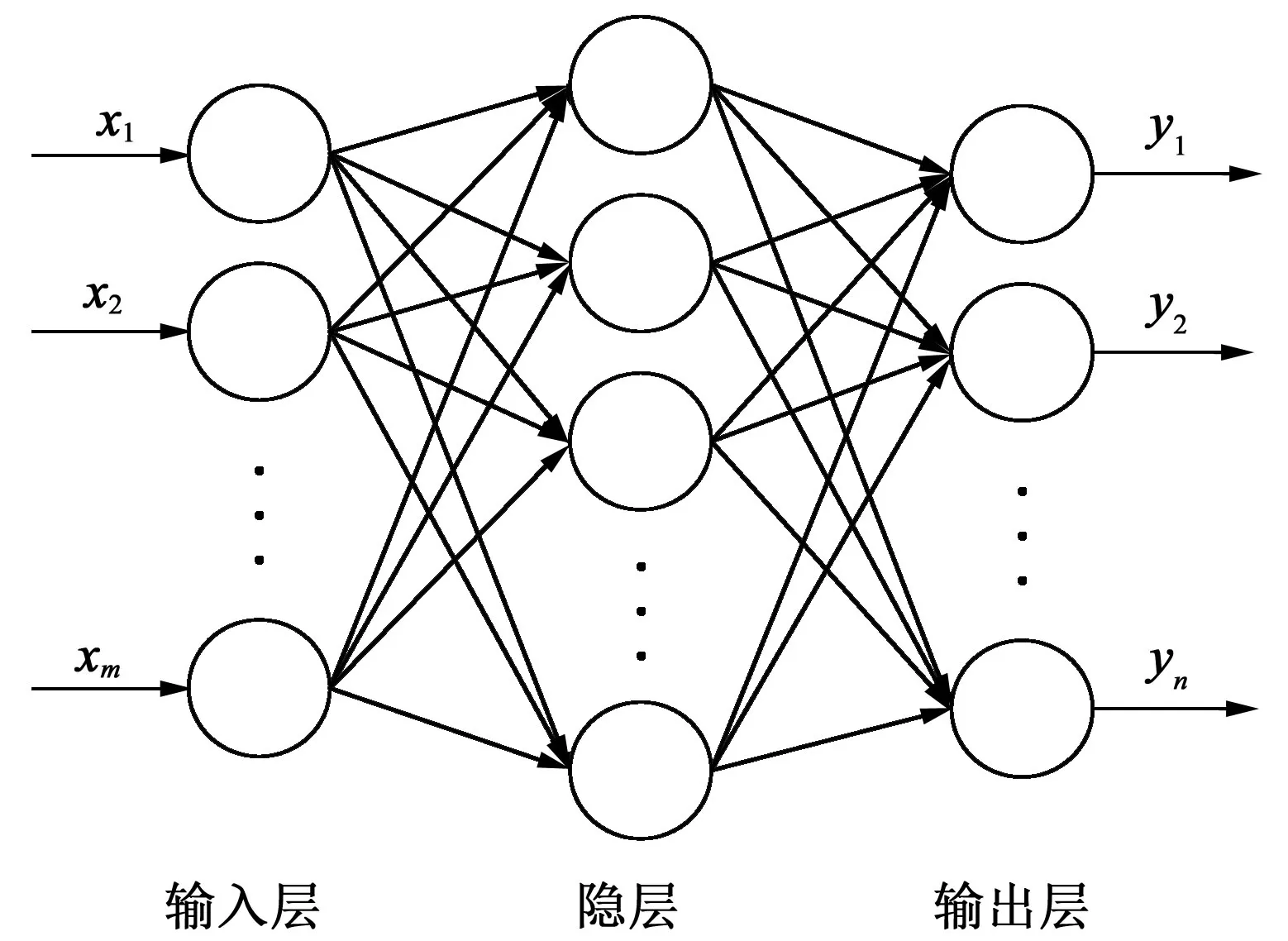
图1 BP神经网络模型示意图Fig.1 Schematic diagram of BP neural network model
本文中采用的技术路线如图2所示。
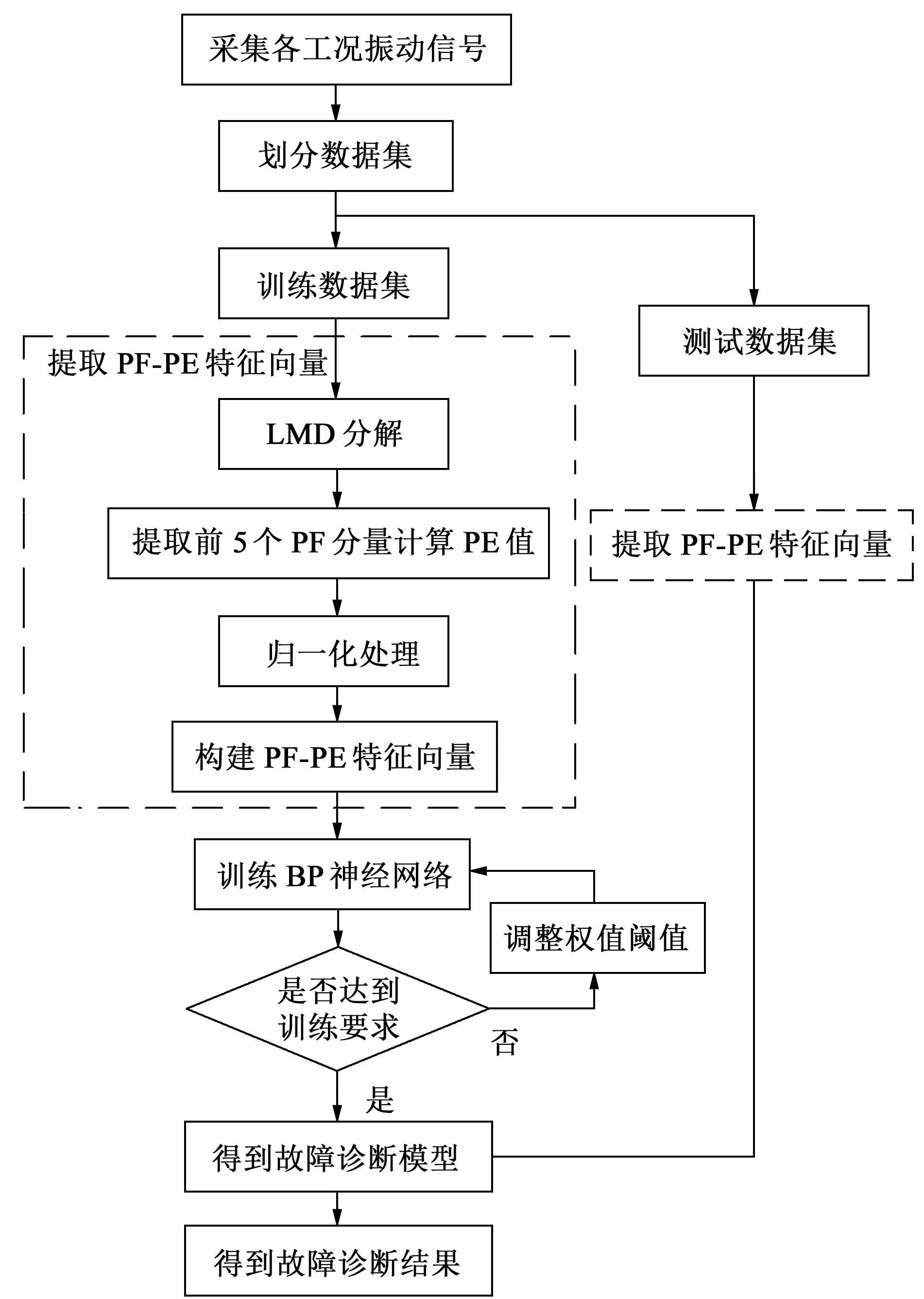
图2 技术路线图Fig.2 Technology roadmap
2 实验验证
2.1 实验装置
为了验证该诊断方法的准确性,搭建了电封闭试验台进行验证。通过PLC 控制输入端的驱动电机和输出端的负载电机,使行星齿轮箱在一定的转速和转矩条件下运行;共采集7个测点的振动加速度数据,具体的测点布置情况如图3所示。齿轮箱为2KH行星齿轮箱,部分参数如表1所示。

表1 齿轮箱参数Tab.1 Parameters of gearboxes

图3 传感器测点布置图Fig.3 Diagram of sensor measuring point layout
以行星齿轮为测试对象,共设置正常、点蚀故障、裂纹故障、断齿故障4种工况,如图4所示。另外,将3 个行星齿轮中的两个同时更换为图4(b)和图4(c)所示的故障行星齿轮。分别采集不同工况下的振动加速度数据,采样频率设置为8 192 Hz。

图4 齿轮不同故障状态Fig.4 Gears in different fault states
2.2 齿轮箱故障故障诊断效果验证
以输入端转速50 r/min,转矩100 N·m 运行试验台,待稳定后开始采集数据。每类工况采集20 s 的数据,取前10 s 数据为训练数据,后10 s 数据为测试数据。在每类工况的测试数据中随机取出30 组连续数据,每组数据长度为32 768,即4 s 的连续数据,进行LMD 分解,并取多个PF 分量求PE 值,最终得到30 组多维特征向量作为训练组。按照相同的方法,在每类测试数据中取得50 组特征向量作为测试组。数据处理完毕后,训练BP神经网络。
以出现点蚀的行星齿轮振动信号为例进行LMD分解,共分解出8 个PF 分量,如图5 所示。其中,图5(a)所示为PF 分量的时域图,图5(b)所示为对应PF分量的频域图。先分解出的PF分量主要包含高频段的信息,后分解出的PF 分量包含低频信息,且伴随着分解的进行,PF 分量的频率成分和有效信息越来越少。因此,分析故障特征时,可选取前几个包含有主要特征信息的PF分量来构建特征向量。

图5 点蚀工况振动信号LMD分解结果Fig.5 LMD decomposition results of vibration signals in pitting condition
点蚀工况分解出的各PF 分量与原始信号间的相关系数如表2 所示。前5 个PF 分量与原始信号的相关度较高,而从第6 个PF 分量开始,相关系数小于0.1。因此,选取前5 个PF 分量计算PE 值来构建故障特征向量。
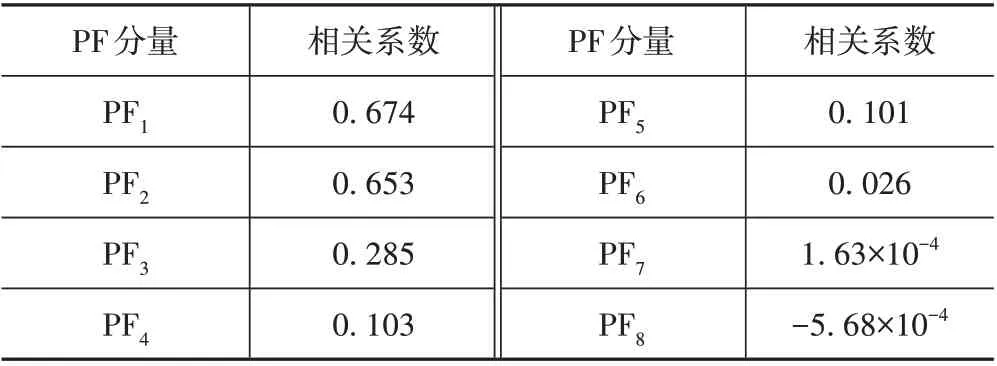
表2 相关系数表Tab.2 Correlation coefficients
图6所示为多种工况下前5个PF分量排列熵值的情况。不同工况PF分量的PE值分别在一定范围内波动,且波动的范围交集较少,这说明各工况PF 分量的PE值具有很好的区分度,适合构建故障特征向量。
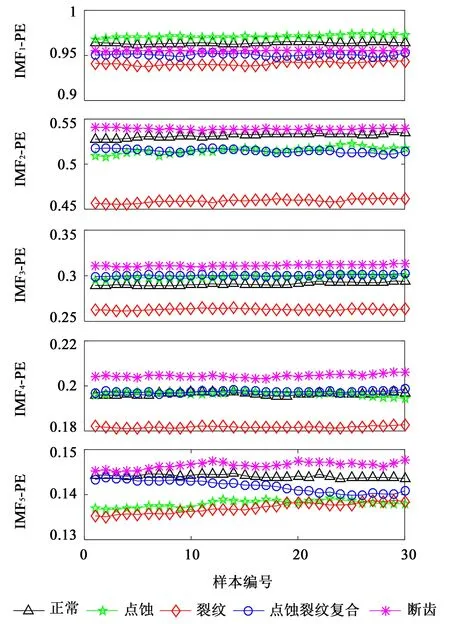
图6 前5个PF分量排列熵值Fig.6 Permutation entropy of the first 5 PF components
神经网络隐层节点个数可根据公式S=x+y+a计算得到。式中,S为隐层节点个数;x、y分别为输入层和输出层节点数;a为1~10 的常数。隐层节点个数对诊断成功率的影响如图7所示。
分析图7 中可知,当选用不同的隐层节点数时,诊断成功率会产生一定的波动,但当隐层节点数取6~14 之间的值时,总体的诊断成功率维持在较高的水平。隐层节点数取13 时,能够取得最理想的诊断效果,诊断成功率为100%。因此,使用该方法取得的特征数据训练神经网络时,应设置隐层节点数为13。
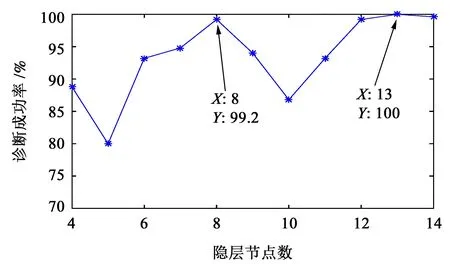
图7 不同隐层节点数的诊断成功率Fig.7 Diagnosis success rate of different hidden layer nodes
为了验证该方法的优越性,另外利用经验模态分解加排列熵方法(EMD-PE)和无量纲分析方法(DIM)作为对比组。使用EMD-PE 方法时,取前5 个IMF 分量的PE 值构造特征向量;使用DIM 方法时,取峭度指标、波形指标、裕度指标、脉冲指标、峰值指标构造特征向量。
多种工况下前5 个IMF 分量PE 值的情况如图8所示。对比分析图8 和图6 中可知,使用EMD-PE 方法构造的特征向量虽然对当前5种工况具有一定的区分度,但其区分效果明显比LMD-PE 方法的区分效果差。分析图9中的结果可知,DIM 方法对断齿故障最为敏感,而对早期故障的区分度很低,这说明无量纲分析方法比较适合分辨程度严重的故障。3种方法的故障诊断结果如图10所示。

图8 前5个IMF分量排列熵值Fig.8 Permutation entropy of the first 5 IMF components

图9 DIM方法分析结果Fig.9 Analysis results with DIM method
图10 中,横轴为样本编号,纵轴为故障标签。其中,1~50 组为正常工况样本;51~100 组为点蚀故障样本;101~150 组为裂纹故障样本;151~200 组为点蚀裂纹复合故障样本;201~250 组为断齿故障样本。3 种方法得到的故障诊断结果用预测结果来表示,通过对比实际结果和预测结果,即可验证是否诊断成功。
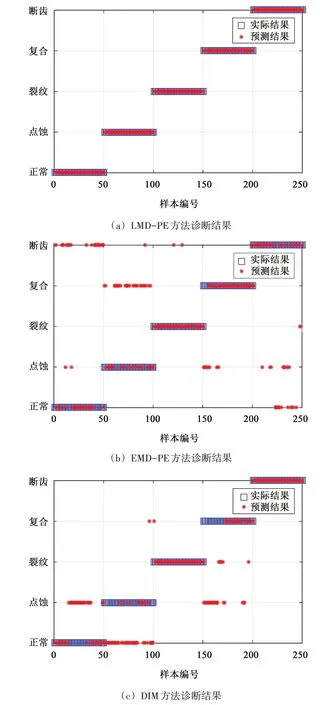
图10 3种方法诊断结果Fig.10 Diagnosis results of three methods
由图10 中的结果可知,LMD-PE 方法的诊断效果最为理想,所有预测结果均与实际结果相符,诊断成功率达到了100%,说明LMD-PE 方法取得的多种工况对应的特征向量间具有明显的区分度;EMD-PE 方法的诊断效果次之,只有2 组裂纹故障被误判为断齿故障,且发生较多误判的断齿故障中也只有1 组被误判为裂纹故障,说明该方法对裂纹故障的区分度较强,但正常状态和断齿故障之间、点蚀故障和复合故障之间均发生了较多的误判,说明该方法除了对裂纹故障诊断效果较好之外,对其余工况的诊断效果都不理想;DIM 方法的综合故障诊断成功率最低,该方法虽然能够完全分辨出断齿故障,但对正常状态、点蚀故障、复合故障3 种工况的诊断效果都不太理想,正常状态和点蚀故障之间出现了很多误判,说明该方法对早期故障的诊断效果很差,且有一定数量的点蚀裂纹复合故障被误判为单一的点蚀或裂纹故障,说明该方法对单一故障和复合故障的区分效果较差。将图10(c)中的诊断结果与图9 中相结合,印证了无量纲分析方法只能较好分辨出故障程度较严重故障的分析结果。以上3 种方法对5 种工况(每种工况50 组测试样本)诊断成功率的具体统计结果如表3 所示。

表3 3种方法的诊断成功率Tab.3 Diagnosis success rate of three methods%
表3 中的平均诊断用时是指单组振动序列样本经过数据处理后,输入至训练好的神经网络模型中,最终得到输出结果所用的时间。由表3 中的结果可知,DIM 方法的数据处理过程简单,诊断效率最高,但其诊断效果最差;而LMD-PE 和EMD-PE方法由于使用了排列熵,运算较为复杂,因此,数据处理时间较长,但最终得到的诊断结果要优于DIM 方法;尤其是LMD-PE 方法,其对不同故障状态特征向量的区分度以及诊断成功率都远高于DIM方法,同时,LMD-PE 方法的诊断效率又比EMDPE 方法有明显的提升。
在实际应用中,训练样本的数目往往会对诊断成功率造成一定影响。本文中通过改变每类工况的训练样本数,并保持测试样本数不变,研究了训练组数对3种方法诊断成功率的影响。
图11 所示为3 种方法分别设置不同训练样本数的诊断成功率。分析图11 可知,3 种方法在每类工况训练样本小于5组时,增加训练样本数会明显提高诊断成功率;当训练样本大于6组时,LMD-PE 方法的诊断成功率高于EMD-PE 方法和DIM 方法,且LMD-PE 方法增加训练样本时,诊断成功率仍然有一定的提升趋势,而EMD-PE 方法和DIM 方法的诊断成功率则在较低的水平波动;在训练样本大于8组时,LMD-PE 方法的诊断成功率稳定在80%以上。综上所述,在训练样本数发生变化时,LMD-PE 方法的表现优于EMD-PE方法和DIM方法。

图11 不同训练样本数的诊断成功率Fig.11 Diagnosis success rate with different numbers of training samples
3 结论
提出了一种基于LMD排列熵和BP神经网络的行星齿轮箱故障诊断方法,并搭建试验台,以行星齿轮故障为例进行了研究。采集正常、点蚀、裂纹、点蚀裂纹复合、断齿5 种工况的数据,提取PF 分量的排列熵值作为特征向量,输入BP 神经网络,实现了多种故障模式的诊断识别,并与EMD-PE 方法和DIM方法对比,得到如下结论:
(1)针对设置的5种工况,由所提出的方法提取出PF 分量排列熵值构成的特征向量明显比EMD-PE方法和DIM方法更具有区分度。
(2)神经网络隐层节点数设置为13 时,所提出方法可实现对5种工况的完全识别。
(3)相比于同样使用排列熵计算的EMD-PE 方法,LMD-PE方法诊断效率更高。
(4)训练样本数发生变化时,LMD-PE 方法的综合表现要优于EMD-PE方法和DIM方法。

