可持续闭环供应链网络的多目标优化研究

刘秀磊，杨玉香

中国计量大学 经济与管理学院，杭州 310018

随着全球工业化进程的不断加快，资源紧缺、环境污染等社会问题日益严重，可持续发展理念越来越被各国所重视。在这样的背景下，很多企业开始建立闭环供应链网络，通过构建回收加再制造的生产模式，将市场上的废旧产品变为可持续发展的战略资源。闭环供应链网络设计作为一项重要的战略决策，直接影响产品的生产、销售、回收以及运输等各个环节，合理的闭环供应链网络设计不仅可以降低企业的运营成本，还可以减少企业运营过程中的碳排放量[1]，同时，还能够使企业更好地履行其社会责任，这对企业探索可持续发展模式有非常重大的意义[2]。

近年来，针对可持续供应链网络优化问题，国内外学者不再只关注经济因素的影响，而是从经济效益和环境效益双维度视角研究该问题[3]。如Yu等[4]构建多目标模糊-随机优化模型，探讨经济效益与环境效益的均衡问题；高举红等[5]构建了双目标优化模型，分析了碳补贴政策对消费者需求偏好以及网络优化过程的影响；孙浩等[6]考虑了环保约束对网络设计的综合影响；Imen 等[7]探讨了消费者的环保意识对供应链网络构建成本的影响；唐金环等[8]研究了在低碳、低成本的决策目标下，库存策略等运营决策对设计结果的影响。可见，双目标供应链网络优化的研究成果已经非常丰富，但却鲜有学者研究经济、环境及社会效益三维度下的网络优化问题，且在少数涉及到社会效益维度的研究中，也主要是用顾客满意度、服务水平、工人福利等指标来衡量社会效益目标[9]，相较于创造更多的就业岗位，这些指标没有更好地体现企业的社会责任。Gao等[10]虽然将提供就业岗位作为决策目标之一，但是社会效益目标的取值完全受另外两个决策目标支配，并未对决策过程产生影响。

相较于传统的正向供应链网络，闭环供应链网络又涵盖了旧产品的回收再制造过程，其设计同样是两级决策。在设施选址决策层面，已有研究证明相较于新建回收设施，通过设施改造构建多功能共享设施可有效降低总成本和总碳排[11]；而在运营决策层面，Sazvar等[12]证明了有效的网络柔性设计可以显著提高网络弹性，同时，Yu等[4]也验证了当市场需求小幅度增长时，为满足刚性的需求约束，新建一个生产厂是非常不明智的行为。然而在现有文献中，却鲜有学者综合考虑设施改造和柔性供应策略对闭环供应链网络设计的影响。此外，在设计闭环供应链网络时，还面临很多不确定性因素的干扰，现有的解决方法主要有鲁棒优化、模糊规划、随机规划等。如董海等[13]就构建了鲁棒优化模型，用多面体不确定集描述不确定因素；李进等[14]则针对很多参数缺少精确统计数据的问题，构建了多目标模糊规划模型；Li等[15]针对设备故障率等因素的随机性，建立了两阶段的随机规划模型；陈勇等[16]还构建了区间机会约束下的易逝品供应链网络优化模型。在以上研究中，均是采用单一方式对不确定性因素进行描述，然而不同参数具有不同的特性，只有基于相关参数的特性选择相应的处理方式，才能构建更为稳健的闭环供应链网络。

综上所述，在闭环供应链网络优化的研究领域，仍存在以下三方面值得去深入研究：（1）构建可行的社会效益目标函数，探讨企业的社会责任对网络优化影响；（2）同时将设施改造和柔性供应策略的理念融入模型的构建过程；（3）基于不同不确定参数的区别，选用相应的处理方法。基于此，本文将经济成本最小、碳排放量最低、创造就业岗位最多作为决策目标，并且将设施改造、外包等柔性供应策略作为决策变量引入模型，建立了多目标的多情景-模糊优化模型。然后运用模糊规划和随机规划两种方法处理模型中的不确定参数，即考虑不同情境下回收品质量水平的随机性，并针对仓储成本、回收成本等参数缺少精确统计值的问题，用三角模糊数的原理将其转化为清晰形式。关于模型求解，本文根据不同的分析角度，分别用线性加权法和NSGA-Ⅱ算法进行求解。最后，通过算例验证模型的有效性，并给出相应的决策建议。

1 问题描述与假设

考虑原有的供应链网络由生产商、分销商和消费者群构成，现需要在原有网络的基础上，新建生产厂，扩大生产规模，同时构建旧产品的逆向回收系统，形成闭环的供应链网络。新建生产商的候选位置已知，而如何构建回收系统却面临着两个方案：一是对现有分销商进行改造，使其具备分销能力外，还能够对旧产品进行回收处理；二是建设新的回收中心。如图1 所示，在正向物流中，生产商负责生产产品，然后经由分销商卖给消费者；在逆向物流中，回收中心和部分被改造过的分销商负责回收旧产品，并对旧产品进行分解处理，然后将可用的零部件运送至生产商进行再制造。在构建模型时，还需要考虑设施改造、柔性供应策略（外包、雇用临时工或加班等）对网络设计的影响，同时考虑回收品质量水平的不确定性，以及网络设计过程中各类成本参数的模糊性。

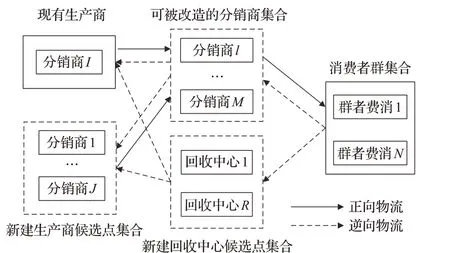
图1 闭环供应链网络Fig.1 Closed-loop supply chain network

为了方便构建模型，需做出以下假设：

（1）商品的运输过程不存在越级运输的情况，均按照供应链中所规划的路径进行；

（2）生产的再制品和新产品性能和售价都相同；

（3）经回收处理后得到的零配件，符合生产标准；

（4）产品与生产原料的生产比例为1∶1；

（5）各候选制造商的生产力有限，分销商和回收中心的容量有限，以及回收处置中心处理废旧产品的能力有限。

2 参数说明

3 模型构建

3.1 经济可持续性目标函数

经济效益目标为总成本最小，如式（1）所示：

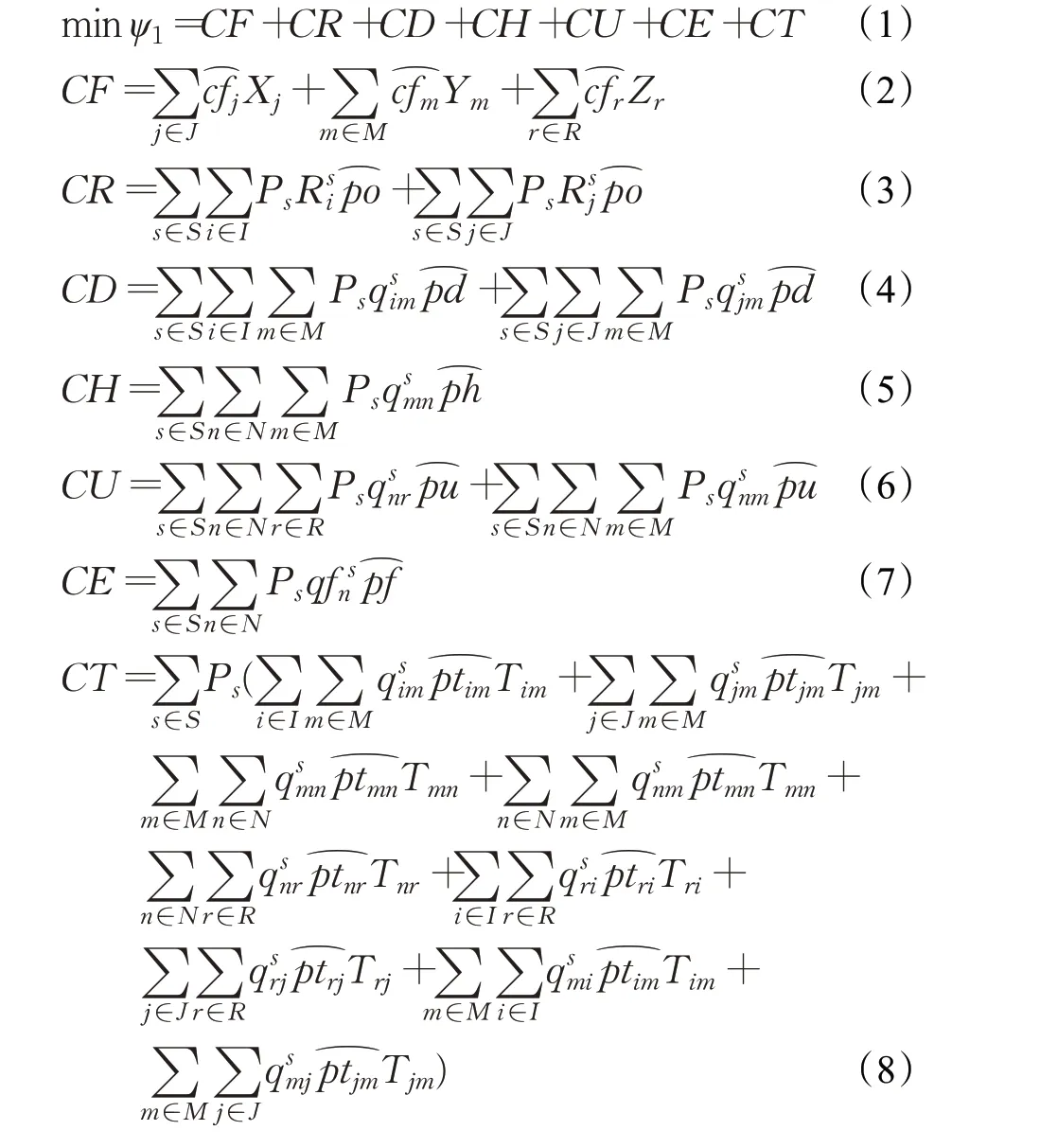
总成本又分为七部分，其中：式（2）为固定成本（CF）；式（3）为原材料采购成本（CR）；式（4）为生产成本（CD）；式（5）为存储分销成本（CH）；式（6）为回收成本（CU）；式（7）为柔性策略生产成本（CE）；式（8）为运输成本（CT）。

3.2 环境可持续性目标函数

环境可持续性的目标为最小化总碳排放量，如式（9）所示：

其中，式（10）为设施建设过程中的碳排放量（EF）；式（11）为生产过程中的碳排放量（ED）；式（12）为回收过程中的碳排放量（EU）；式（13）为运输过程中的碳排放量（ET）。

3.3 社会可持续性目标函数

社会可持续性的目标是创造更多的就业机会，如式（14）。重新设计闭环供应链网络会提供更多的就业岗位，这些工作岗位主要来源于设施建设过程以及废旧产品的回收过程。具体计算公式如下：

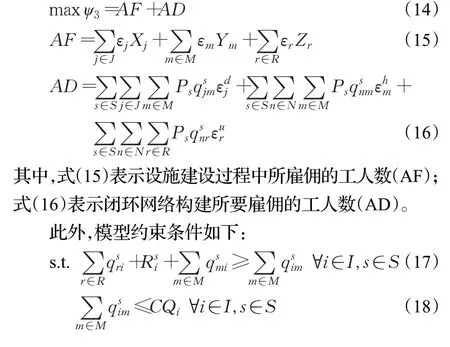
其中，式（17）表示现有生产商的流量平衡约束；式（18）描述现有生厂商的生产能力限制约束；式（19）为新建生厂商的流量平衡约束；式（20）表明若未在j点建厂，则该设施点不能接收任何物资；式（21）为新建生产商的生产能力约束；式（22）表示分销商的流量平衡约束；式（23）表示市场需求必须被满足；式（24）表明消费市场的回收量不能超过销售量；式（25）、（26）分别是对被改造的分销商和新建回收中心的回收处置能力的限制约束；式（27）、（28）为回收的废旧产品可用于再制造的比例约束；式（29）为柔性供应策略的限制约束；式（30）、（31）、（32）为建设生产商和回收中心，以及改造分销商的数量约束；式（33）、（34）为决策变量约束。

3.4 模型拓展

模型中包括固定建设成本、生产成本、回收成本等成本参数均具有模糊性，为将其转化为清晰形式，首先引入三角模糊数[17]的概念对这些模糊参数进行定量化处理。设a=(al,am,ah) 为任意模糊三角数（如图2 所示），其中al，am，ah分别为悲观下界估计、最可能的取值估计以及乐观上界估计，满足al≤am≤ah，式（35）为其隶属度函数μa(x)[4]。

图2 任意三角模糊数a=(al,am,ah)Fig.2 Arbitrary triangular fuzzy numbers a=(al,am,ah)

4 模型求解

为了能够从社会总成本的角度来研究供应链网络优化问题，首先，需要用线性加权法[18]将模型转化为单目标规划形式，并且为了统一量纲，又引入了碳税率(Tax)和平均人工成本(Cp)两个参数，然后对3个目标分别赋予权重w1、w2、w3，则社会总成本SC可以表示为式（45）：

minSC=w1ψ1+w2(Taxψ2)-w3(Cpψ3) （45）

上述问题的约束条件不变。容易看出，该单目标规划模型自变量的一阶导数均为常数，所以模型是线性的，因此，可以直接调用MATLAB2019a 中的intlinprog函数求解该规划问题。

此外，在多目标供应链网络优化问题中，不同的目标间相互制约，一个目标的优化可能就会降低其他目标的期望值，所以当决策者基于不同偏好去做决策时，往往不好直接比较所得结果的优劣。因此，为了更好地权衡目标间的关系，就需要找到问题的Pareto解，Pareto解集可以更好地呈现出目标间的冲突，便于后面进行多目标的权衡性分析。NSGA-Ⅱ算法是一种基于遗传算法求Pareto 解集的进化算法，常用于求解多目标优化问题。相较于传统的NSGA算法，NSGA-Ⅱ提出了快速非支配排序法，降低了算法的复杂程度；并提出了拥挤度比较算子，有效保持了群体的多样性，同时给出了精英策略，在求Pareto 前沿的过程中扩大了采样空间[19]。NSGA-Ⅱ算法的主流程步骤如下[20]：

（1）编码及初始化种群

首先，本文研究的是供应链网络优化问题，为了将备选方案的具体信息映射到基因编码中，需要采用两段式实数编码的方式构建染色体，两段码串分别表示设施选址以及设施点间的物料配置。染色体结构X如式（46）所示：

式中的xi表示第i个设施选址变量，xj表示第j个物料运输变量，且取值均为整数。如对包含2个供应商、1个分销商以及1 个零售市场的三级供应链网络进行优化，需要对供应商进行选择并配置设施点间的物料。假设X=( 0 1|0 100 50 )，就表示选择第2个供应商为分销商供货100件，且从分销商运送至零售市场50件。基于以上方法进行编码并初始化种群，种群规模为200。

（2）非支配排序法

对本文建立的多目标优化问题，首先确定成本最小和碳排最小的目标分量f1(x)=ψ1，f2(x)=ψ2，并且为了方便计算，需要将3 个目标统一为求解最小值，所以社会效益最大的目标分量需要取相反数，即f3(x)=-ψ3。若∀i∈{1,2,3} ，都满足fi(xa)≤fi(xb)，则可以称个体a支配个体b。如果在整个种群中，不存在能够支配a的其他个体，则称个体a为非支配个体。从初始种群开始，逐级筛选非支配个体，并根据级别给定不同的标签，直至所有个体都得到一个等级标签，等级越小的个体越优。

（3）拥挤度比较算子

（4）精英保留策略

将迭代后的子种群和父代种群融合为新的种群，然后根据非支配排序法进行分级，按照由低等级到高等级的顺序，选出部分个体作为子代，同等级的个体则根据拥挤度大小进行筛选，直至选出的个体数目达到规定的子代种群规模。

（5）交叉与变异

本文采用的是随机单点交叉，对于两个父代个体，随机选择两个子串X1、X2进行交叉。首先，随机确定一个交叉点，并生成一个随机数s，s∈{0,1}，当s为0时，对交叉点后面部分进行交叉，否则对前面部分进行交叉，交叉概率经过试验设置为0.75。

在供应链网络设计的过程中，设施点间的供应关系是具有连续性的，因此，为了防止高变异率使得最优解被破坏，将变异概率设置为0.05。

5 算例分析

现以某家电企业为案例背景进行算例分析，并考虑3种设施选址规模，分别为算例Ⅰ（1×2×2×3×2）、算例Ⅱ（1×3×3×4×3）、算例Ⅲ（2×4×4×6×4）。关于参数赋值，回收的旧产品的质量水平是不确定的，因此在进行闭环供应链网络优化时，需要考虑多种情景，表1给出了不同情境下的相关参数值。此外，参考高举红等[5]及李进[21-22]的数值算例，并结合同类型企业的调研数据，以及不同算例间生产规模的差异，确定了相关成本参数的三角模糊数值，以及设施容量和单周期内的市场需求量；同时，参考李进[21-22]采用ECO-it1.4软件及数据库来估算各环节碳排放量的方式[22-23]，对所需的各项碳排放系数进行估值；最后，通过参考同类型企业的生产规模和工人数量，估算设施建设和运营所提供的岗位数量。取值如表2所示。

表1 不同情境下的参数设定Table 1 Parameters setting in different situations

表2 参数取值Table 2 Parameters value

5.1 目标权重的灵敏度分析

为了研究目标权重的变化对社会总成本SC的影响，对目标权重进行了灵敏度分析。首先，赋予经济目标的权重w1，w1∈{ }0.3,0.4,0.5,0.6,0.7,0.8 ，然后基于w1的数值，赋予社会效益目标的权重w3，例如，当w1=0.3 时，w3∈{ }0,0.1,0.2,0.3,0.4,0.5,0.6,0.7 ，最后赋予环境目标的权重w2=1-w1-w3，并将其他参数经处理后代入模型，求解结果如图3所示。

如图3 所示，3 个算例中的社会总成本随权重变化的波动趋势是一致的，因此，以算例Ⅱ为代表，进行具体的权重灵敏度分析，如图3 所示，可以看出社会总成本变化具有以下4 个特征：（1）在给定经济成本权重w1时，随着社会效益权重w3的增大，社会总成本SC 呈现出先递减后递增的趋势，如图3（a），当w1=0.3 时，随着w3的增大，社会总成本SC由134.38先降至132.13后增加至266.68；（2）随着w1的增加，为了使社会总成本SC取得最小值，所允许的社会效益最大权重w3是逐步降低的，由0.4(w1=0.3)降低到了0.1(w1=0.8)，w3如果大于这个界限值，SC 将会大幅度增加；（3）如果不考虑碳排放量，即w2=0 时，不管w1、w3取值如何变化，社会总成本SC 均取得各情景下的最大值，如图3（b），当w1=0.4、w3=0.6 时，社会总成本取得该情境下的最大值260.15；（4）随着w1的增加，每个情景所对应的最大社会总成本逐步降低，w1＞0.6 后，SC 最大取值稳定在177.92。算例Ⅰ、算例Ⅲ的求解结果同样具有以上4 个特征，基于上述分析，可以得到以下结论：

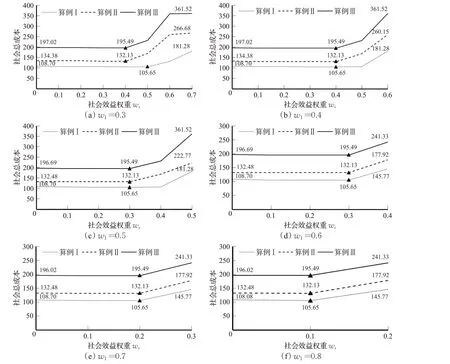
图3 社会总成本与权重设置的关系Fig.3 Relation between total social cost and weight setting

（1）对于3 个目标的权重，使任何一个等于0，都会使得社会总成本SC 增大，所以在进行闭环供应链网络优化时，系统考虑经济、环保、社会效益的影响会显著降低社会总成本。

（2）经济成本目标的权重不应该小于0.6，这是为了降低成本过高的风险，将每种情景所对应的最大社会总成本控制在一定范围；同时，为了获得最低的社会总成本，社会效益目标权重不应该大于0.4。

5.2 模型的稳健性分析

为了研究多目标情景优化模型的稳健性，本文分析了需求扰动水平对设计结果的影响。基于线性加权的处理方法，分别设置w1=0.6，w2=0.2，w3=0.2，然后求出总需求在不同波动水平下的优化结果，社会总成本变化见图4，选址结果见表3。如图4所示，对于3种不同规模的算例，均存在一个市场需求波动区间，使得该区间内社会总成本SC 的波动幅度相对较小；当需求变化超出了该区间，社会总成本的波动幅度显著增大，而造成这一现象的主要原因是设施选址结果的差异。以算例Ⅰ的选址结果为例，如表3所示，市场总需求在65 000至70 000 波动时，选址结果是相同的，所以该阶段的社会总成本SC 的波动幅度最小；即便当市场需求超出了该区间范围，如65 000至80 000，新建生产商(J)的选址结果仍然相对稳定，此时，如图4（a）所示，虽然社会总成本的波动幅度也会变大，但主要是源于回收设施(M、R)选址的变化；只有当需求波动过大，如小于60 000时，新建生产商(J)的选址结果才会发生变化。以上分析也同样适用于其余2个算例的优化结果，这也证明了在构建模型时，考虑不同参数的不确定性和柔性供应策略的影响，可以获得比较稳健的闭环供应链网络优化结果。

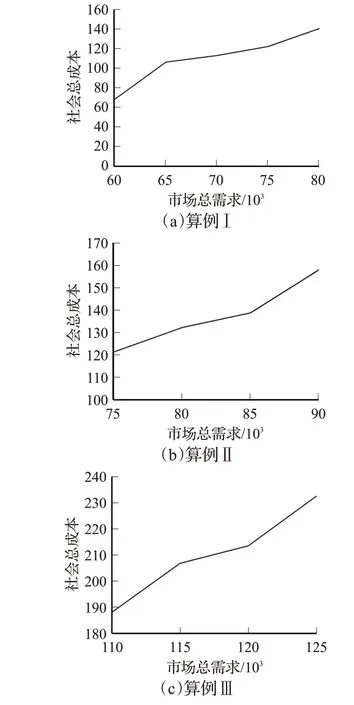
图4 不同市场需求下的社会总成本Fig.4 Total social cost under different market demands

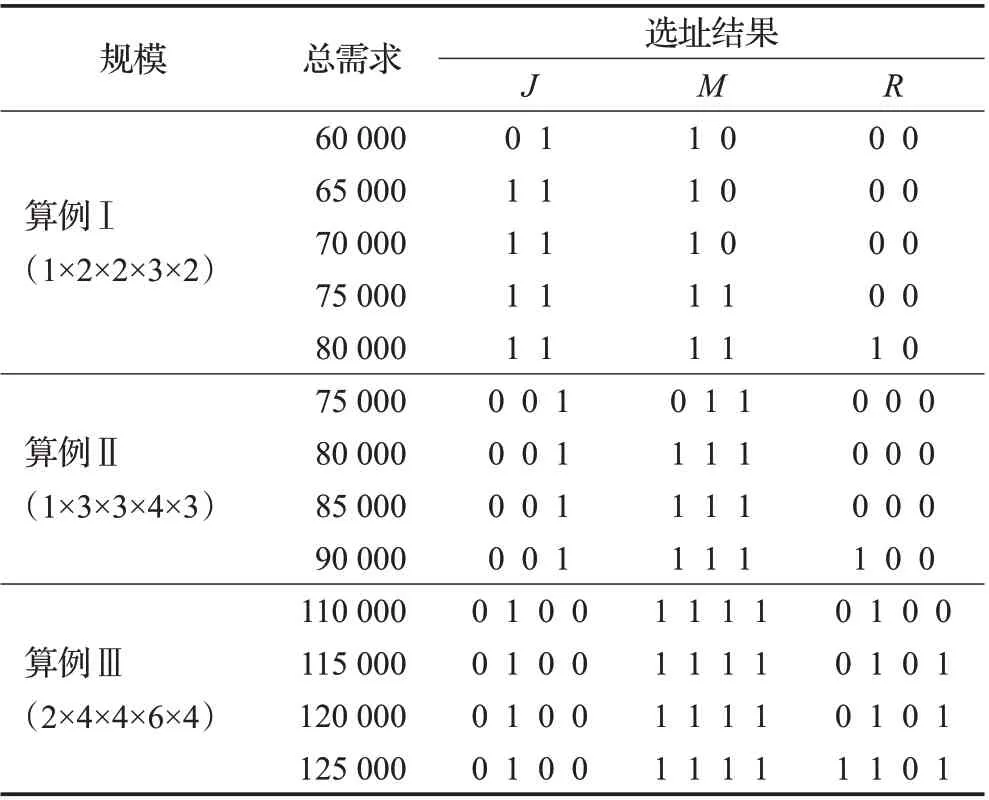
表3 不同需求下的选址结果Table 3 Location selection results under different demands

5.3 有无设施改造的模型对比分析

在建设逆向回收系统时，本文选择了设施改造和新建设施并举的构建模式，为分析该模式的优劣性，运用线性加权法处理多目标函数，首先设置w1=0.6，w2=0.2，w3=0.2，然后求出在不同的市场需求下，有无设施改造两种模式下的优化结果，见表4。在无设施改造的模式下，不对分销商进行改造，所以只有新建的回收中心具有回收职能。如表4所示，相较于重新构建回收设施，采取设施改造和新建设施并举的模式，可以显著降低社会总成本。

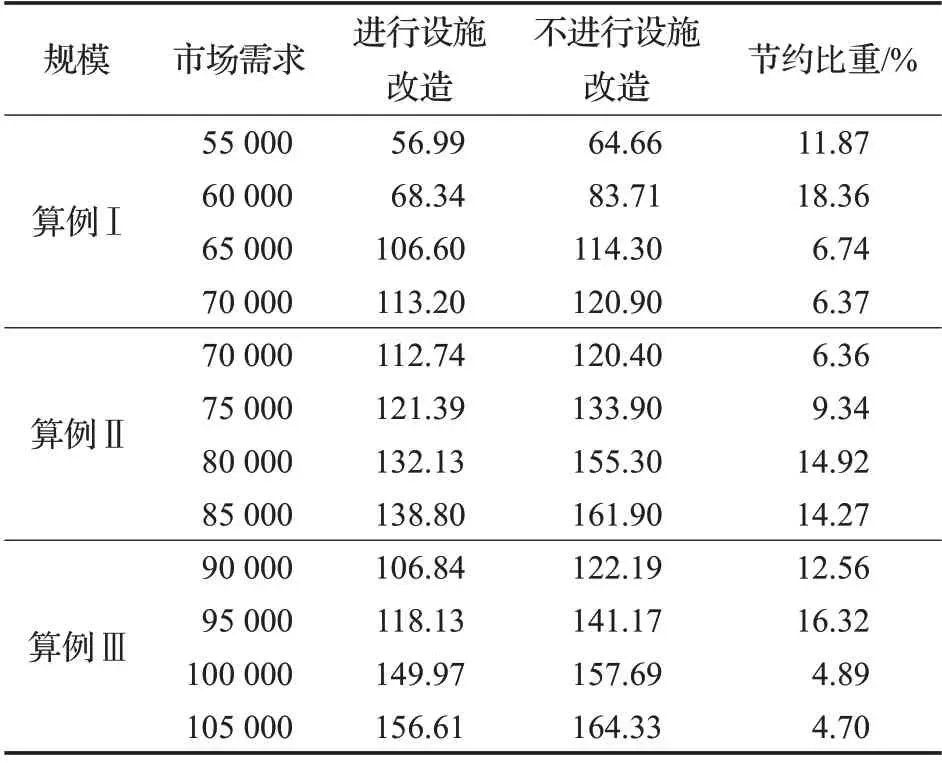
表4 设施改造前后的社会总成本对比Table 4 Comparison of total social costs before and after facility renovation

5.4 有无柔性供应策略的模型对比分析

为了研究柔性供应策略对闭环供应链网络设计的影响，基于线性加权法，分别求出不同的市场需求下，考虑柔性供应策略与不考虑柔性供应策略两种情景下的优化结果。如图5所示，对于3种不同规模的算例，考虑外包等柔性供应策略的影响，均可以显著降低社会总成本。基于算例Ⅱ的选址结果，可以判断社会总成本的差异主要源于设施选址的差异，如表5所示。特别是当市场需求大于85 000 时，两种情境下的生厂商(J)选址结果差别尤为显著。这也符合现实情境，当市场总需求在某个区间内小幅度变动时，相较于扩建生产设施来增加产能，采用外包等策略来弥补产能的不足是更好的应对方法，这也说明了在构建闭环供应链网络模型时，考虑柔性供应策略的影响是非常必要的。

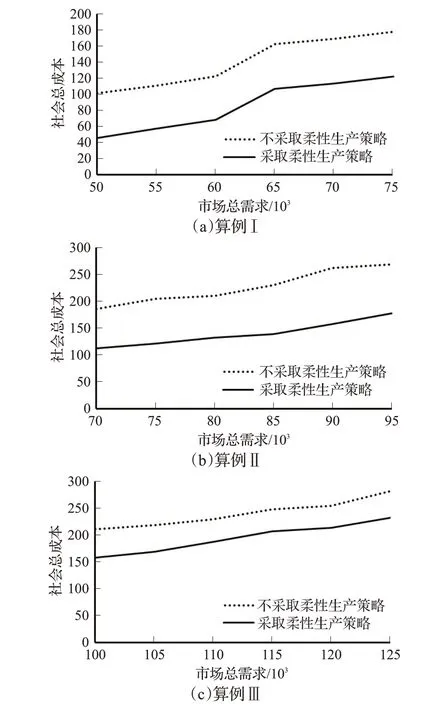
图5 采用柔性供应策略对社会总成本的影响Fig.5 Influence of adopting flexible supply strategy on total social cost

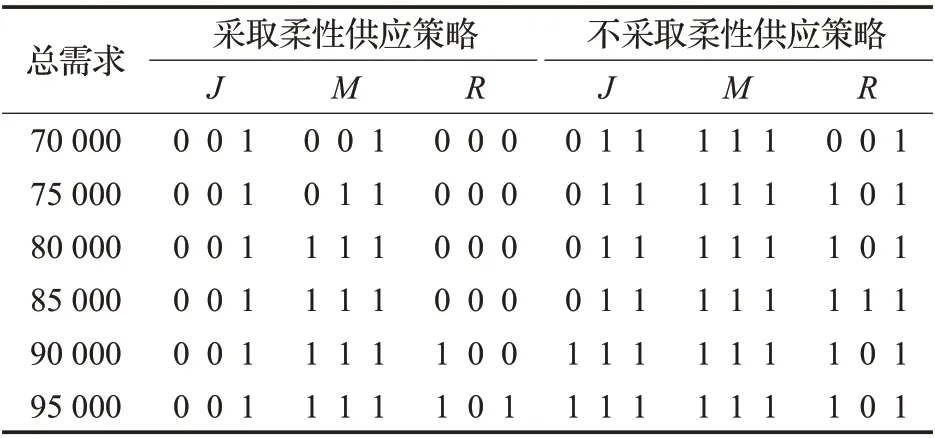
表5 算例Ⅱ采取柔性供应策略前后的选址结果Table 5 Site selection results before and after adopting flexible supply strategy of example Ⅱ

5.5 多目标的权衡分析

为了进一步对3个目标进行权衡性分析，本文运用NSGA-Ⅱ算法求出了3 种闭环供应链网络规模下的Pareto 解集，结果如图6 所示。由图6 可以看出，3 个算例所得Pareto解分布的相对位置相似，说明目标函数间的相对关系并不受算例规模的影响。

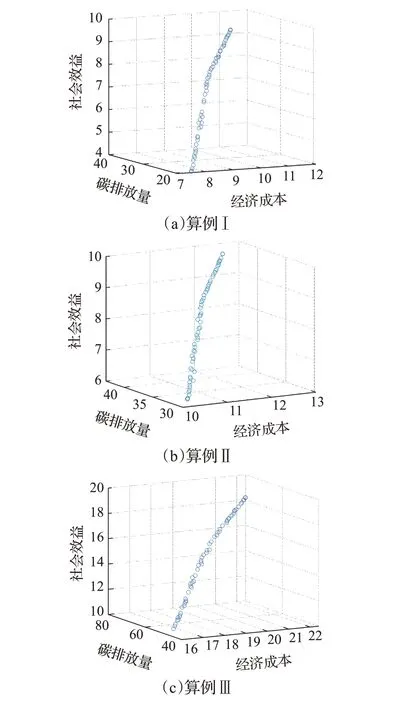
图6 Pareto解集前沿分布图Fig.6 Front distribution diagram of Pareto solution set

为了更直观地呈现各个目标间的关系，以算例Ⅱ为例分析，将所得Pareto 解进行分解处理，结果如图7 所示。由图7所示，碳排放量和经济成本间存在正相关关系；社会效益和经济成本同样呈现出正相关关系，并且在某个界限值后，斜率发生了变化，这种相关趋势同样适用于社会效益与碳排放量。通过对以上几点进行剖析，可以得到3个结论：（1）经济成本与碳排放量是同步变化的；（2）社会效益目标和经济成本、碳排放量这两个目标均存在冲突；（3）加大成本投入，可以有效提高社会效益，但是当成本投入超过某个点，这种效用就会下降，此时，为了实现社会效益同等幅度的增长，就需要付出更大的经济与环保上的代价。

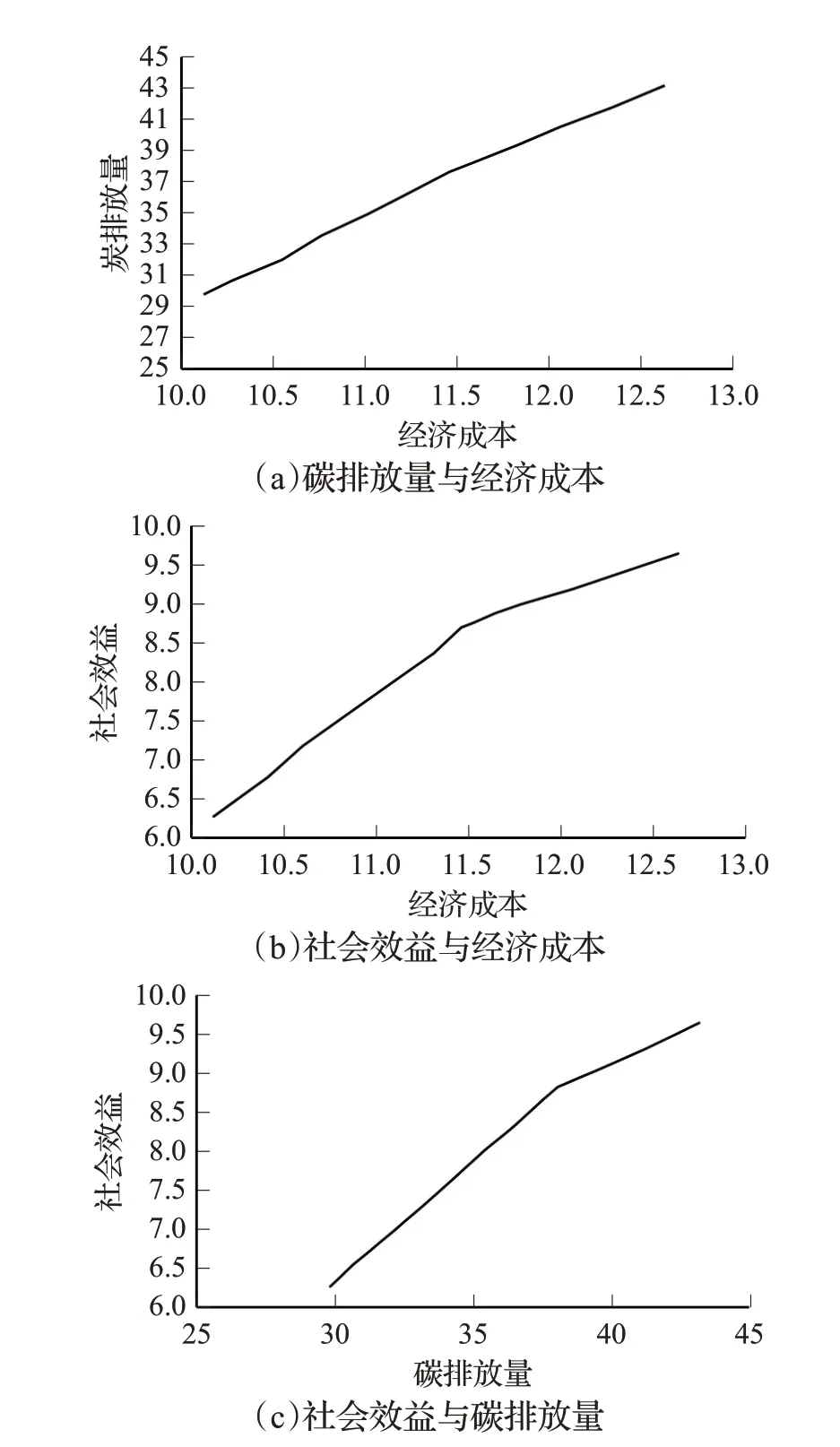
图7 3个目标间的关系图Fig.7 Diagram of relationship between three objectives

6 总结

本文针对闭环供应链网络优化问题，构建了可持续的多目标多情景-模糊优化模型，同时考虑了经济成本、碳排放量、社会效益3 个目标，并考虑了回收产品质量水平的不确定性以及各类成本参数的模糊性。最后，分别用线性加权法和NSGA-Ⅱ算法对多目标模型进行了求解，所得结论如下。

（1）在设计闭环供应链网络时，综合考虑经济、环境以及社会责任的影响，可以显著降低社会总成本，而且为了使得社会总成本最低，应该仍以经济目标为主，然后给予环境目标和社会效益目标足够的重视。

（2）在运营决策层面考虑柔性供应策略以及参数的不确定性，可以使构建的网络优化模型更为稳健。并且通过模型对比，证明了采用设施改造和柔性供应策略的方案均可以显著降低社会总成本。

（3）通过对多目标进行权衡性分析，讨论了各个目标间的冲突，发现经济成本与碳排放量是同步变化的，两个目标间存在正向相关关系，而社会效益目标与经济、环保目标是冲突的，所以为了提升社会效益，就需要加大另外两方面的投入。值得注意的是，随着投入超过某个界限值，这种投入的回报效用就会降低。

本文是在单周期的背景下进行闭环供应链网络设计研究的，在未来，可以考虑在多周期的运营背景下进行研究，并且进一步优化社会效益的衡量指标体系。