基于参数自学习的无人车越野环境跟踪控制方法

吴永刚，梁华为，余 彪，孙 超

1.安徽大学 物质科学与信息技术研究院，合肥 230601

2.中国科学院 合肥物质科学研究院，合肥 230088

在抢险救灾、消防救援、军事作战等典型应用领域[1-2]，往往要求无人车具有高度灵活的机动性，且需要兼顾跟踪精度和行驶稳定性，准确的模型和合理的控制律设置是路径跟踪控制算法的关键[3]。

在现有的控制理论领域，传统控制算法如比例积分微分（PID）控制[4]、纯跟踪控制算法[5]，这些控制算法利用几何关系，在一个或多个预瞄位置计算误差，只能在一定范围内简单适用。为了适应更多场景，研究人员探索了如模糊控制[6]、滑模控制[7]等方法，然而这些控制方法只能对当前状态量计算控制动作，无法预测未来状态信息，且无法处理如偏离轨道等极限工况。为了提高控制器的鲁棒性和保持车辆航向的能力，文献[8]提出了鲁棒控制器，将车辆航向偏差用于跟踪误差建模，可以在一定干扰条件下减小车辆航向偏差。文献[9]提出了一种通过跟踪车辆航向来计算转向的控制器，并通过低摩擦系数的路况实验来验证该控制器。然而这些控制器没有考虑车辆运动过程中的瞬时动力学特性，如在侧滑等情况时，减小航向偏差的同时无法保证横向偏差较小。模型预测控制方法（model predictive controller，MPC）能够有效处理车辆和轮胎动力学[10-11]，且考虑的是未来一段时间内的最优控制量，因此有利于提高车辆控制稳定性[12]。但在进行高速复杂路况的路径跟踪时，这些基于固定参数模型设计的控制器无法克服车辆未建模的不确定性和复杂路况的干扰，难以保证稳定的跟踪性能。随着人工智能和传感器技术等的发展，文献[13]有效考虑模型偏差的问题，基于模型预测控制建立学习的高斯扰动模型，但其超参数选择较为复杂，文献[14]采用模糊算法自适应调整MPC 的权重系数，以改善跟踪性能，但并不能克服不确定性干扰的影响。文献[15]提出了一种数据驱动的无模型自适应控制方法，用于无人驾驶车辆横向运动控制，这种方法的参数需要大量数据集进行训练，文献[16]考虑了未建模的车辆非线性动力学和道路不确定性，通过无模型的迭代学习控制方法研究赛车的跟踪控制，这种方法适合参考轨迹固定的路径跟踪，遇到新的场景和干扰需要重新进行训练学习来确定参数。

考虑到在高速跟踪越野环境复杂路况的场景，无人车在高速运动过程中的非线性动力学特性较为复杂，无法建立精确的车辆动力学模型，导致控制参数和控制律设置较为困难[17]，并且越野环境下复杂路况不断变化的曲率和路面条件、地形因素等也给路径跟踪控制带来了影响[18]，这使得现有的路径跟踪控制技术难以满足跟踪精度和稳定性要求。

针对越野环境下高速跟踪复杂路况的任务需求，为了减小模型失配和道路曲率等干扰带来的影响，本文基于车辆动力学误差模型，设计了一种在线更新学习系数的参数自学习前馈控制器（parameters self-learning feedforward controller），与模型预测控制方法构成前馈-反馈控制框架，并在越野路况进行了实验验证。越野环境实车实验结果表明，相比传统模型预测控制方法，所设计的控制器在跟踪精度和稳定性上都有较大改善。

1 车辆模型

1.1 车辆动力学模型

无人车以较高的速度在越野环境下进行复杂路况的路径跟踪时，简单的车辆运动学模型难以满足复杂工况下的车辆行驶的瞬态特性和稳定性需求。因此，进行了车辆动力学模型的建立，基于车辆单轨模型，如图1所示，推导出了车辆运动过程中的状态量与控制量前轮偏角之间的关系式。

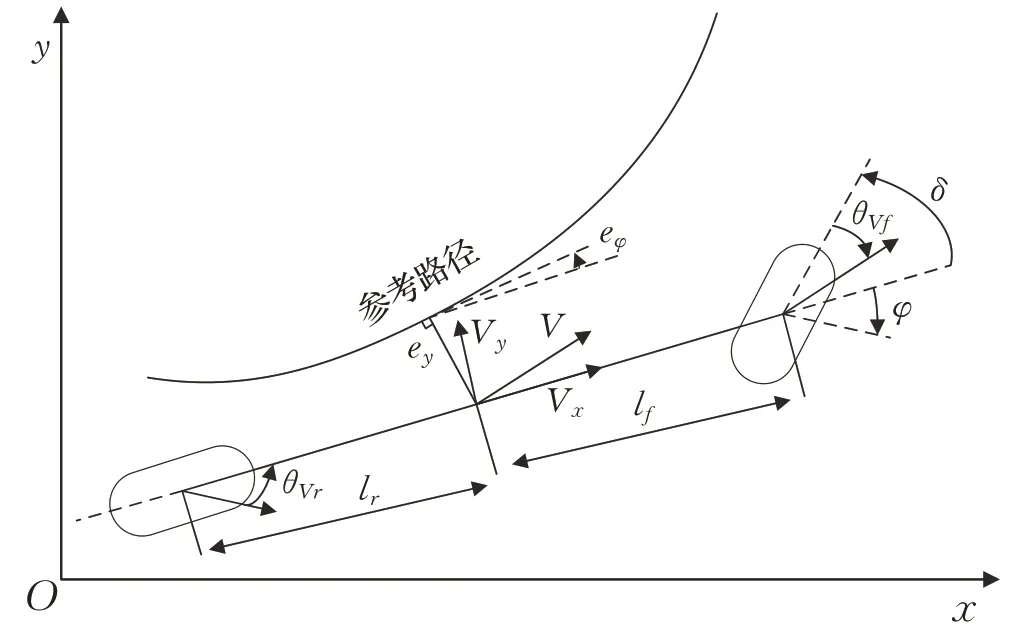
图1 车辆单轨模型Fig.1 Vehicle monorail model

车辆动力学模型采用的状态量：y表示车辆横向位置信息，φ表示车辆偏航角信息，δ为前轮偏角，经推导计算可得到如下车辆动力学模型状态方程：

其中，m为整车质量，Iz为车辆绕z轴转动的转动惯量，Vx为车辆速度，lf和lr为车辆质心距前、后轴的距离，Cαf和Cαr为车辆前、后轮的侧偏刚度。

1.2 车辆动力学误差模型

在复杂环境下，为有效提高无人车路径跟踪精度，使用相对于参考路径的位置误差和航向角偏差作为动力学模型的状态变量建立动力学误差模型，求解控制变量前轮偏角。因此，在现有车辆动力学模型的基础上经推导可得出以下基于跟踪误差变量的状态空间模型：

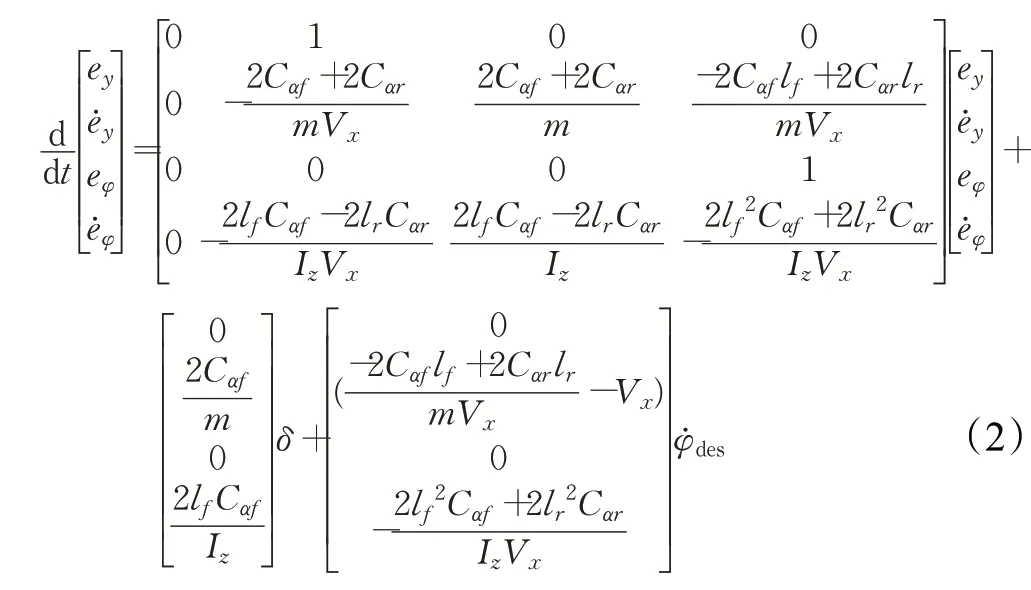
式中，ey为横向误差，eφ为航向偏差，φ̇des为参考横摆角速度。

2 控制器设计

传统控制方法基于误差模型在参考路径附近近似线性化，没有考虑车辆动力学模型与实际系统的不匹配，此外，路况等实验环境存在无法建模的干扰，如路面起伏颠簸程度、土壤条件等，导致路径跟踪控制器的效果难以达到预期目标。基于动力学误差模型，设计了一种参数自学习控制器结构，前馈控制器根据误差在线更新学习系数，模型预测控制器作为反馈控制。控制器结构如图2所示。

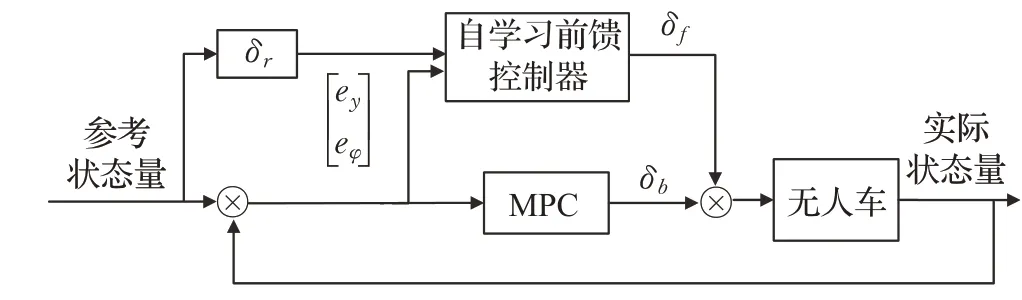
图2 控制器框图Fig.2 Controller block diagram

如式（3），控制输入由前馈动作和反馈动作组成：

其中，δb为反馈控制输入量，δf为前馈控制输入量，在以下小节中阐述。

2.1 反馈控制量求解

式（3）中反馈动作δb由动力学MPC 计算所得，考虑以下动力学线性时域模型：

式中，Np和Nc分别为预测时域和控制时域，Q和R是系统权重矩阵，η为状态向量，Δu为控制量增量。

在每个控制周期完成上述求解后，得到控制时域内的一系列输入增量：

2.2 前馈控制量求解

前馈控制动作δf由参数自学习控制算法求得：

式中，δr为参考前馈控制动作，由参考路径信息获得。L和H为前馈控制输入的更新系数，也即参数自学习控制算法所要求解的学习系数。

3 自学习前馈控制器设计

3.1 学习系数

由上述动力学误差模型，得到控制量和横向误差及航向误差的表达式：

其中，λ为正的常数，即λ ＞0，也就是说，如果代价函数E收 敛 于0，则 满 足 鲁 棒 控 制 性 能 条 件，ëy+2λėy+λ2ey=0，ëφ+2λėφ+λ2eφ=0，也即横向误差和航向误差收敛于0。

梯度下降法是一种寻找函数最小值的一阶迭代优化算法，在这种方法中，步长的取值与闭环误差函数梯度的负值成正比，以下用梯度下降法寻找代价函数E的最小值：

故而，前轮偏角的前馈控制输入表达式中的学习系数L的更新式为：

3.2 稳定性分析

代价函数E是半正定的李雅普诺夫函数，即E≥0，为验证参数自学习控制算法的稳定性，将李雅普诺夫函数E对时间求导数：

可知，如果学习系数选取合适，李雅普诺夫函数E的时间导数为负，即Ė＜0，证明参数自学习控制算法的渐进稳定性。

3.3 收敛性分析

参数自学习控制算法中还需要考虑的问题是系统可能会停留在某些局部极小值而无法求得全局最小值解。接下来我们将分析参数自学习控制算法是否能够跳出局部最小值，求解出全局最小值，这里取代价函数

式（22）和式（23）表明前轮偏角的代价函数的二阶导符号是正的，因此没有局部最小值，这就说明系统达到了全局最小值，由于α为常数，δr是有界的，表明学习系数收敛到有界值，稳态下系数的有界值计算出有界前馈动作。

4 实验验证

4.1 实验平台

实验平台采用的是基于奇瑞瑞虎车改装后的“智能先锋号”无人车，车载感知系统有64线激光雷达1台、彩色摄像头1台以及GPS惯导组合导航系统，计算平台配有两台工控机，自动驾驶软件架构包含感知、决策、规划、控制四部分，相互之间进行TCP 通信，各自并行计算。实验平台如图3所示，平台参数如表1所示。

图3 实车实验平台Fig.3 Real vehicle experimental platform

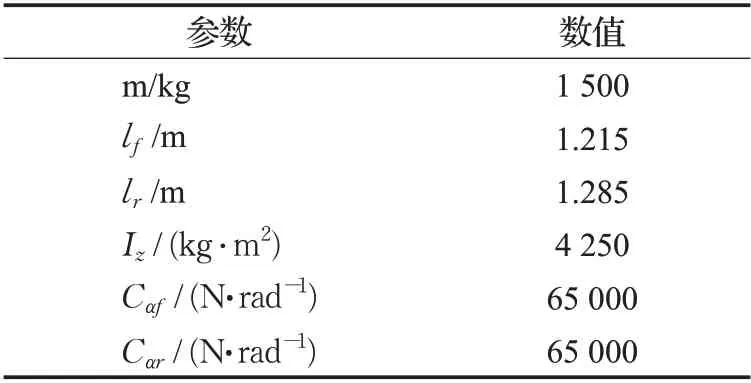
表1 实车平台参数Table 1 Parameters of real vehicle platform

4.2 实验方案

为保证路径跟踪实车实验的安全性以及有效性，选取了起伏颠簸的砖石场地和起伏大曲率的越野路面两个实验场景分别进行30 km/h速度下的直角转弯路径跟踪和50 km/h速度下的S型路径跟踪实验，如图4和图5所示。初始时，车辆位置从参考轨迹起点出发，航向与参考轨迹初始方向一致。每组实验分别进行多次，选取其中3 组较为合理的实验数据取平均值进行数据处理。实验参数设置如表2所示。

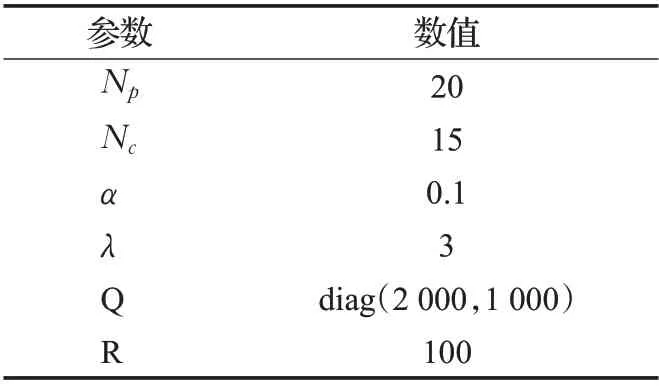
表2 实验参数Table 2 Experimental parameters

图4 直角弯实验场地Fig.4 Right-angle turning experimental site

图5 S型实验场地Fig.5 S-type path experimental site

4.3 实验结果

本次实验目的为验证所设计的参数自学习控制器的路径跟踪控制效果，并与不加前馈控制的模型预测控制器（MPC）的路径跟踪控制结果对比，实验结果对比图如图6 和图7 所示，控制器A 代表所设计的参数自学习控制器结构，控制器B代表传统模型预测控制器。横向误差和航向误差分别代表了无人车控制算法位置跟踪和航向跟踪的能力；横摆角速度和车辆的稳定性直接相关，且极限值与路面摩擦系数等道路条件有关。这里只考虑数值大小，分别对直角弯路径跟踪和S型路径跟踪两种路况下的实验数据进行了分析处理，处理结果如表3所示。

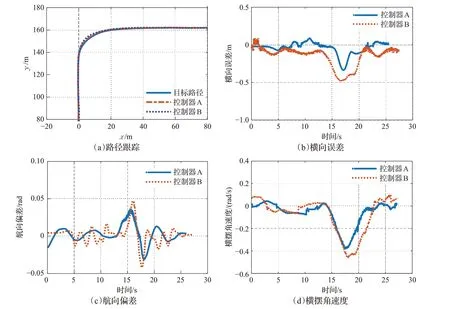
图6 直角型路径跟踪实验结果对比Fig.6 Comparison of experimental results of right-angle path tracking

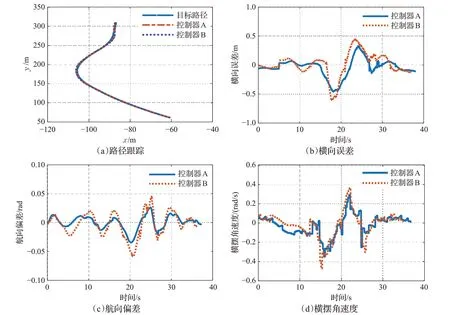
图7 S型路径跟踪实验结果对比Fig.7 Comparison of experimental results of S-type path tracking

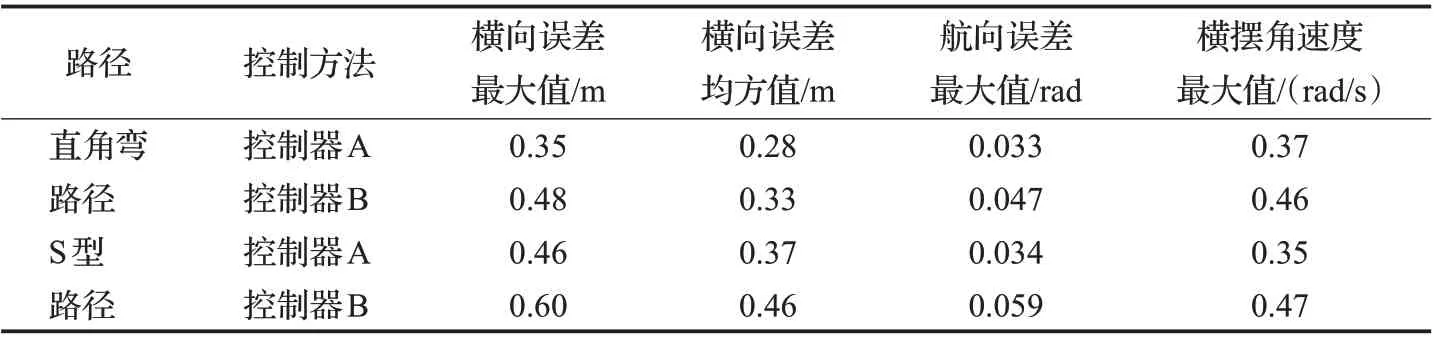
表3 实验数据Table 3 Experimental data

由实验结果对比图分析，误差的波动是因为高速跟踪起伏颠簸的复杂路况需要及时地修正误差，而误差较大的地方是在道路曲率快速变化的地方，这也说明了高速复杂路况路径跟踪的控制难点，结合实验数据表格，与模型预测控制（MPC）相比，所设计的参数自学习控制器在两种高速越野场景下的路径跟踪实验中横向误差和航向误差都较小，表明所设计的控制器比MPC 跟踪精度更高；且在两种路况下，所设计的控制器的横摆角速度最大值在极限值范围内比MPC 更小，表明路径跟踪过程中车辆横摆稳定性更好，安全性更高，验证了所设计的控制器能够在一定程度上克服车辆动力学未建模的不确定性和路况的干扰对路径跟踪控制带来的影响，相比模型预测控制（MPC）有着更好的跟踪控制性能。

5 结束语

针对越野环境下高速复杂路况的路径跟踪场景，为了克服车辆动力学未建模的不确定性和道路条件的干扰，提高跟踪精度和车辆行驶稳定性，以车辆动力学误差模型为基础，设计了一种参数自学习的前馈补偿控制器，与模型预测控制构成前馈-反馈的控制器结构，根据实时状态的误差大小在线更新前馈控制器参数，自适应调整前馈控制动作和反馈控制动作的权重，并在野外场景进行了复杂路况的实验验证。实验结果表明，与传统的模型预测控制（MPC）相比，所设计的控制器在两种场景下路径跟踪的横向误差和航向偏差更小，横摆角速度也在稳定范围内有所减小，即所设计的控制算法在进行高速复杂路况的路径跟踪中，跟踪精度和车辆稳定性都有所改善，能够保证较好的路径跟踪性能。