“倍长中线”的“源”点
——中点
文/武益燕
全等三角形的对应边相等、对应角相等这一性质,决定了全等三角形是转化线段、角的有力“武器”。可在解决问题的过程中,常常事与愿违——没有全等三角形。那我们如何转化呢?
例如图1,在△ABC中,AD为边BC上的中线。求证:AB+AC>2AD。

图1
【分析】要证“AB+AC>2AD”,我们容易联想到“三角形两边之和大于第三边”。而AB、AC、AD不是同一个三角形的边,因此,我们可以转化线段,将它们集中到同一个三角形里面。由“AD为边BC上的中线”可知,BD=CD。我们可以尝试延长AD,构造对顶角,则有一组边和一组角相等,再适当构造一组相等的边或角,全等就在眼前!比如,如图2,延长AD到点E,使得DE=AD,无论是连接BE还是CE,都能得到“八字形”全等,从而构造出我们要求的三角形。

图2
把结论中的三边集中到同一个三角形,构造全等是解决本题的关键!怎么想到作辅助线?唯一的条件“中线”就是突破口。“中线”代表一组边相等,延长中线,便出现对顶角,延长中线一倍,便构造出“八字形”全等。我们不妨把这种方法叫作“倍长中线”,以便理解和记忆。
变式训练如图3,AD是△ABC的中线,E、F分别在AB、AC上,且DE⊥DF,则()。
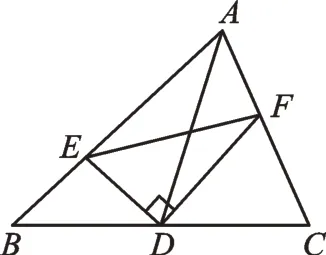
图3
A.BE+CF>EFB.BE+CF=EF
C.BE+CF<EF
D.BE+CF与EF的大小关系不确定
【分析】若按照例题的方法,我们能构造出全等三角形,但无法转化线段BE、CF、EF,故此构造无效。因此,我们需要理解本题的本质。其中D是中点,则BD=CD,若转化CF,应延长FD到G,使得DG=DF,连接BG、EG,如图4。根据两次全等:△CDF≌△BDG,△EDF≌△EDG,便能实现线段转化,最终在△BEG中运用三角形三边关系解决问题。
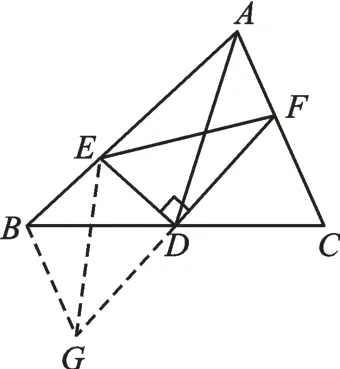
图4
相信你能想到也可以构造全等转化BE,殊途同归!抓住本质,合理构造,就如“倍长中线”的本质不是“中线”,而是“中点”一样。

