基于三维应力状态的静止侧压力系数研究

李顺群，刘继承，刘小兰，张 彦，黄雄飞

(1. 天津城建大学土木工程学院，天津 300384； 2. 天津城建大学天津市软土特性与工程环境重点实验室，天津 300384； 3. 安徽水安建设集团股份有限公司，安徽合肥 230601)

0引 言

静止土压力是设计挡土墙时必须考虑的因素之一，通常作用在刚性很大的挡土墙上，此时挡土墙不发生任何移动或转动，墙后土体处于静止状态[1]。在墙背填土表面下任意深度处的静止土压力可以通过静止侧压力系数K0来衡量[2-4]。作为岩土工程的重要参数，K0的取值直接关系工程设计的合理性与实践性，对计算人工岛屿边界挡土构件的土压力，确定砂砾在压实过程中的应力状态，分析筑坝时防渗墙的变形问题等有较大影响[5-7]。

国内外学者对K0已经进行了大量研究，其中有些因测量手段受到限制，精度不高，导致试验结果没有达到预期值。1965年Komornik等[8]利用电阻应变片来测定K0值，但该研究对应变片的精度要求较高。Abdelhamid等[9]设计了一种测定K0值的固结仪，在该仪器上安装测头便可直接测量侧向压力，但测头技术还不成熟。国内学者袁聚云等[10]通过真三轴仪来控制2个侧向不发生变形，使试样达到K0状态，但这种方法对砂土是否适用尚不明确。蔡正银等[11]针对砂土进行了离心模型试验，通过测量土体的压缩量和铝合金板上的水平土压力来计算K0。事实上，K0的大小受土层土类、深度、应力历史、空间几何特征、土体本身性质等多方面影响。杨瑞雪等[12]以银川地区粉细砂为研究对象，发现细粒含量的增大对粉细砂静止侧压力系数不利。张继周等[13]根据前人推导出的计算公式发现应力历史是影响土体K0值的一个重要因素，墙后填土的空间几何特征对其影响也较为显著。

本文基于土的压缩变形特性，设计制作了一种能够测算静止侧压力系数的圆筒模型试验装置，对天津地区浅层砂土进行了一维加卸载压缩试验。采用天津三为科技有限公司研发的三维土压力盒，研究了不同深度的静止侧压力系数，揭示了K0在不同深度处的变化规律，得到了深度对K0的影响程度，验证了该试验装置的合理性、三维应力测试方法的可靠性以及试验测算得到的K0值的准确性，可为今后天津地区岩土工程相关设计提供技术支持和安全保障。

1模型试验

1.1试验系统组成

本试验使用能够测算土体静止侧压力系数的圆筒模型试验系统，该试验系统包括圆筒模型系统、三维应力测试系统、加卸载系统3个部分。该模型试验系统如图1所示。

图1圆筒模型试验系统构成Fig.1Composition of Cylinder Model Test System

圆筒模型系统采用的装置为圆筒模型箱，该装置包括通过透明密封条连接上筒与下筒形成的圆筒和通过圆筒底部重型钢板的8根钢筋与顶部交叉的2根工字钢构成的反力架，其中工字钢与钢筋之间采用螺母拧紧，圆筒放置于反力架中央处。在不施加外力情况下，将圆筒填满砂土后需保持反力架不受力、不偏移、不弯曲。

三维应力测试系统由2个部分组成，分别为土压力感应装置和外界应力采集系统。土压力感应装置即三维土压力盒，包括1个形状似球的基座、7个小型一维土压力盒以及连接土压力盒的数据导线，其基本原理和具体构造参考文献[14]。该数据导线与型号为DH3816N的静态应力应变测试分析系统相连接，笔记本电脑用来显示采集到的数据曲线图，并与应力分析系统通过无线方式进行连接，由此形成外界应力采集系统。

加卸载系统采用立式液压千斤顶装置，其结构紧凑，可以稳定升起重物，传动效率较高。该装置能够确保额定载重吨位，承重可达20 t。在此次试验中，液压千斤顶在容许应力值0～196 kN范围内为圆筒提供压力，并且可实现加载与卸载。

1.2模型设计与试验方案

基于土的压缩变形特性，本文设计制作了一种圆筒模型，其剖面如图2所示。圆筒与底部钢板构成一个半封闭空间，在圆筒内部填满砂土且不排水，可作为常用的轴对称模型。圆筒的材料为玻璃纤维，上筒和下筒的高度均为80 cm，外径均为71 cm，内径均为70 cm。两筒连接处利用防水薄膜进行密封，下筒与底板之间采用AB胶及防水薄膜加以牢固。

图2圆筒模型设计剖面(单位：cm)Fig.2Design Section of Cylinder Model (Unit:cm)

圆筒开口位置上方预留高度为10 cm的砂土，防止施加压力时圆筒上的混凝土盖板损坏连接土压力盒的数据导线，也可起到观察筒内砂土沉降的作用。钢筋采用HPB235光圆钢筋，在试验中承受拉力作用。千斤顶和混凝土盖板布置在工字钢与圆筒顶部10 cm高的土层之间，前者用来加载和卸载，后者则实现力的传递和转化。

选取天津地区浅层砂土作为试验土样，根据《土工试验方法标准》[15]，得到试验土样的基本物理参数：含水率w=0.63%，最大干密度ρdmax=1.658 g·cm-3，最小干密度ρdmin=1.482 g·cm-3，不均匀系数Cu=1.65，压缩系数Cc=0.94。根据砂土的分类标准，粒径大于0.075 mm的颗粒含量超过全重85%的砂土为细砂，确定该试验土样类型为细砂，其颗粒级配曲线如图3所示。

图3试验土样颗粒级配曲线Fig.3Particle Gradation Curve of Test Soil

在砂土初始密度、颗粒粒径和含水率等不变条件下，利用上面所述的三大系统，进行不同土体深度(距离混凝土盖板底部中心的高度为20、70、120 cm)对砂土静止侧压力系数K0影响的一维压缩试验。试验采用“加载-卸载-稳定”模式，在3个测点各埋置1个三维土压力盒，如图2所示。测试基本原理为：千斤顶施加的荷载通过反力架反向传给混凝土盖板，再传到土体内部，三维土压力盒随即感应到土的压力，再结合文献[14]中的矩阵算法和力学理论即可得到土体内部的三维应力状态。

在本模型试验系统中，梁结构的工字钢刚度大，抗拉强度高，承受较大弯矩时能够达到抗扭抗弯效果，防止出现失稳现象。混凝土盖板内部设有钢筋，抗压强度高，不易变形，具有很强的承载能力，并且能很好地将集中荷载转化为均布荷载。圆筒筒壁厚度大，材料抗拉抗弯能够满足无侧向变形条件。连接工字钢的钢筋韧性好，冷弯性能好，屈服点不明显。底部钢板硬度刚度均较高，试验过程中能够支撑上部所有结构以及土体，且不会发生任何变形。

1.3试验步骤

1.3.1 试样填埋与土压力盒布置

以底部钢板顶面为基准面，将细砂填入圆筒至基准面以上150 cm，并利用振动压实器对试样进行密实。在试样表面的中心处放置1个型号为DTS-2的三维土压力盒，具体位置和方向如图4所示，z轴正方向垂直Oxy面朝外，形成空间坐标系Oxyz。利用通信设备自带的水准仪测量出压力盒位置的倾角，并确保其接近0°。

图4三维土压力盒定位Fig.4Three-dimensional Soil Pressure Box Positioning

按照上述步骤，将距离基准面100、50 cm两处的三维土压力盒埋置好，同样对试样进行分层压实，填埋至筒顶时连接压力盒的数据导线，按设计示意图依次从圆筒内部导出，继续填土至高出筒顶10 cm并压实，如图2所示。

1.3.2 反力架安装与千斤顶放置

待试样填埋完成后，将直径为70 cm、厚度为13 cm的混凝土盖板稳定放置在试样表面，保证板圆心与筒圆心对齐，并尽量防止高出筒顶的砂土撒落。将中心交叉的2根工字钢各端与从底部钢板上各圆孔伸出的2根受力钢筋对应，依次通过螺纹连接进行固定，安装过程中要保证这2根工字钢与基准面平行。在反力架安装结束后，放置千斤顶，其顶部应对准2根工字钢的交叉处，底部与混凝土盖板的中心对齐。

1.3.3 圆筒轴向加载与数据采集

将试样内部导出的数据导线与DH3816静态应力测试分析系统上对应的21个采集通道依次连接，采集箱与笔记本电脑连接。打开系统配套软件，输入三维土压力盒对应的标定系数k后，试验准备就绪。先点击“采集”，再开始施加压力，注意2根工字钢的交叉处、千斤顶的中心和圆筒横切面的中心始终在1条铅垂线上。经过加卸载，待记录仪显示出若干段稳定的曲线，点击“停止”，保存、输出试验数据并导入EXCEL表格，试验结束。

1.4数据采集

试验结束后，将导入EXCEL表格的试验数据整理并绘制曲线，得到在加卸载条件下，土体深度分别为20、70、120 cm处测点的正应力变化曲线，如图5～7所示。其中，正应力σ1、σ2、σ3、σ4、σ5、σ6依次为三维土压力盒接触面a、b、c、d、e、f受到土体的压力，其大小均大于0，方向均垂直接触面朝外。由于采集仪按照试验要求设置的频率为5 Hz，采集点共1 800次，故测试时间为360 s，测试过程可分为加载阶段、卸载阶段以及稳定阶段。

图5土体深度为20 cm的正应力变化曲线Fig.5Positive Stress Change Curves with Soil Depth of 20 cm

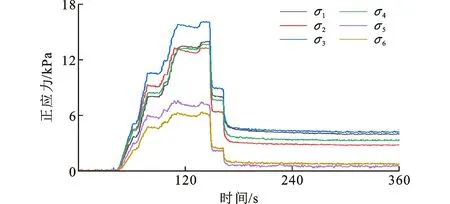
图6土体深度为70 cm的正应力变化曲线Fig.6Positive Stress Change Curves with Soil Depth of 70 cm

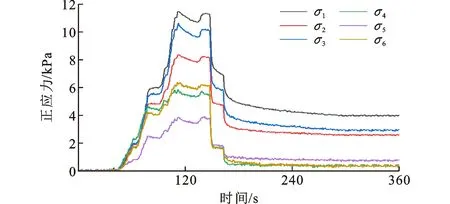
图7土体深度为120 cm的正应力变化曲线Fig.7Positive Stress Change Curves with Soil Depth of 120 cm

2试验结果及分析

2.1三维应力状态分析

根据图5～7所示的正应力变化曲线和文献[14]，通过反算三维应力空间中3个正应力σx、σy、σz与3个剪应力τxy、τyz、τzx的理论公式[式(1)]，并展开成矩阵形式，得到在加卸载条件下，土体深度分别为20、70、120 cm处测点的三维应力状态，如图8～10所示。

(1)

式中：lj、mj、nj分别为第j个正应力σj(j=1,2,3,4,5,6)的方向余弦。

图8土体深度为20 cm处测点的三维应力状态Fig.8Three-dimensional Stress States of Measuring Points with Soil Depth of 20 cm

图9土体深度为70 cm处测点的三维应力状态Fig.9Three-dimensional Stress States of Measuring Points with Soil Depth of 70 cm

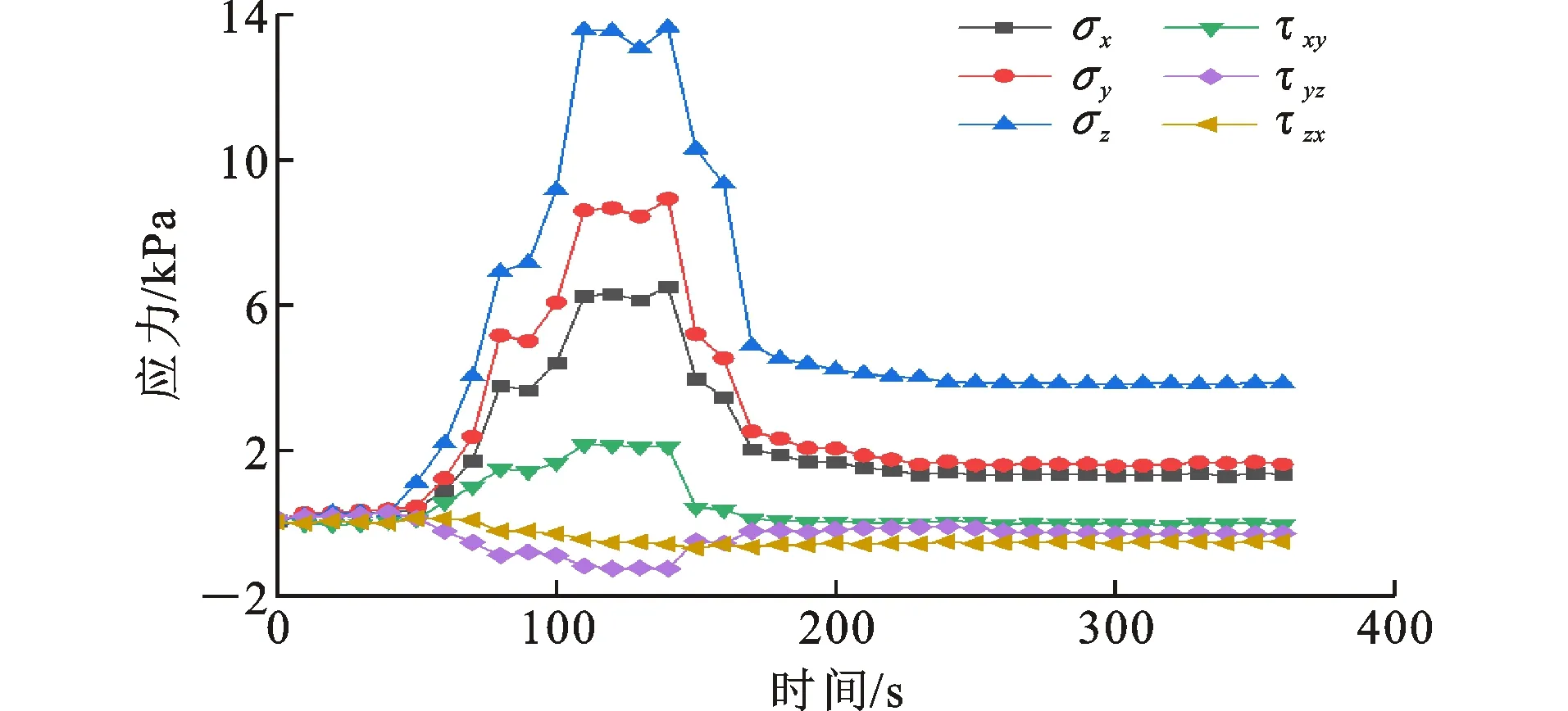
图10土体深度为120 cm处测点的三维应力状态Fig.10Three-dimensional Stress States of Measuring Points with Soil Depth of 120 cm

图8为土体深度20 cm处测点的三维应力状态变化曲线。从图8中可以看出：0～140 s为加载阶段，其中0～40 s为初步加载，应力大小基本没有较大变化，这是由于初步加载中钢筋未完全受拉，土颗粒间的大孔隙消失；该段时间正应力σx、σy、σz和剪应力τxy具有正方向增大趋势，而τyz、τzx具有负方向增大趋势，这是由于土颗粒开始发生相对滑移，剪应力方向与规定的方向不一致，和土压缩时表现出的力学性质相吻合。40～140 s进入正式加载状态，应力不连续性增加，且竖向应力σz最大，达到64.109 kPa，这是因为土颗粒间的孔隙逐渐减小，密实度随之变大；不难看出，有2段时间内应力大小没有明显变化，说明土体在加载过程中具有一定的弹塑性，导致其受到的部分压力抵消。140～240 s为卸载阶段，曲线初期陡降，减少到一定偏差应力时，曲线开始变缓，竖向应力σz减小至26.293 kPa。另外，土体的应力状态并没有完全恢复到原始状态。卸载过程的应力变化一方面是由土体弹性变形引起的，另一方面是由于存在不可恢复的塑性应变。240～360 s为稳定阶段，正应力和剪应力均基本保持不变，说明土体内部已变形破坏。在加载、卸载、稳定3个阶段中，竖向应力σz一直保持最大；相对正应力，3个剪应力均偏小，这些变化均符合土体本身的受力特性和加卸载条件下土体压缩时的力学特征。

图9为土体深度70 cm处测点的三维应力状态变化曲线。与图8比较，应力变化趋势基本一致，不同的是前者在40 s后对应时刻得到的竖向应力σz明显小于后者，且最大值为23.235 kPa。

图10为土样深度120 cm处测点的三维应力状态变化曲线。与图8和图9比较，应力变化趋势基本一致，不同的是该曲线在40 s之后对应时刻得到的竖向应力σz明显小于后两曲线，且最大值为13.634 kPa。

纵观图8～10可知，不同深度处土体受到的竖向应力以及水平向应力均不相等，三维土压力盒测定的σx与σy在加载阶段也不相等，造成这一现象的主要原因有：①三维土压力盒埋置深度较浅，加载过程中会存在偏移情况；②砂土颗粒粒径分布不均匀且其各向异性较显著；③圆筒各处厚度不同且内部刚度也不一致。曲线逐渐平缓后σx与σy接近相等，同时也说明作为新型测试技术手段，三维土压力盒用于测定土中一般应力状态是可靠的。基于李风增[16]研究得到的土压力随深度增加呈非线性变化，本试验得到随着深度增加，竖向应力值变化具有单调性，结合试验数据可知，其明显减小。

2.2静止侧压力系数K0分析

静止侧压力系数K0是岩土工程分析计算中的一个重要参数，定义为土体在无侧向变形条件下，水平向受到的正应力σh与竖向受到的正应力σv的比值[17]。在本试验中，K0表示为x方向的K0x和y方向的K0y，水平向正应力表示为σx和σy，竖向正应力则表示为σz，那么通过式(2)可求得静止侧压力系数。

(2)

根据图8～10及式(2)计算得到不同深度土体的K0值，绘制K0值随时间变化曲线，如图11、12所示。为更好地体现不同深度K0值的变化，横坐标选择三维应力状态变化曲线中50～360 s时间段。显然，土体深度为120 cm的K0值最大，土体深度为20 cm的K0值最小，240 s时曲线形成“平台”，并取最后120 s的K0值作为K0稳定值范围，结果如表1所示。

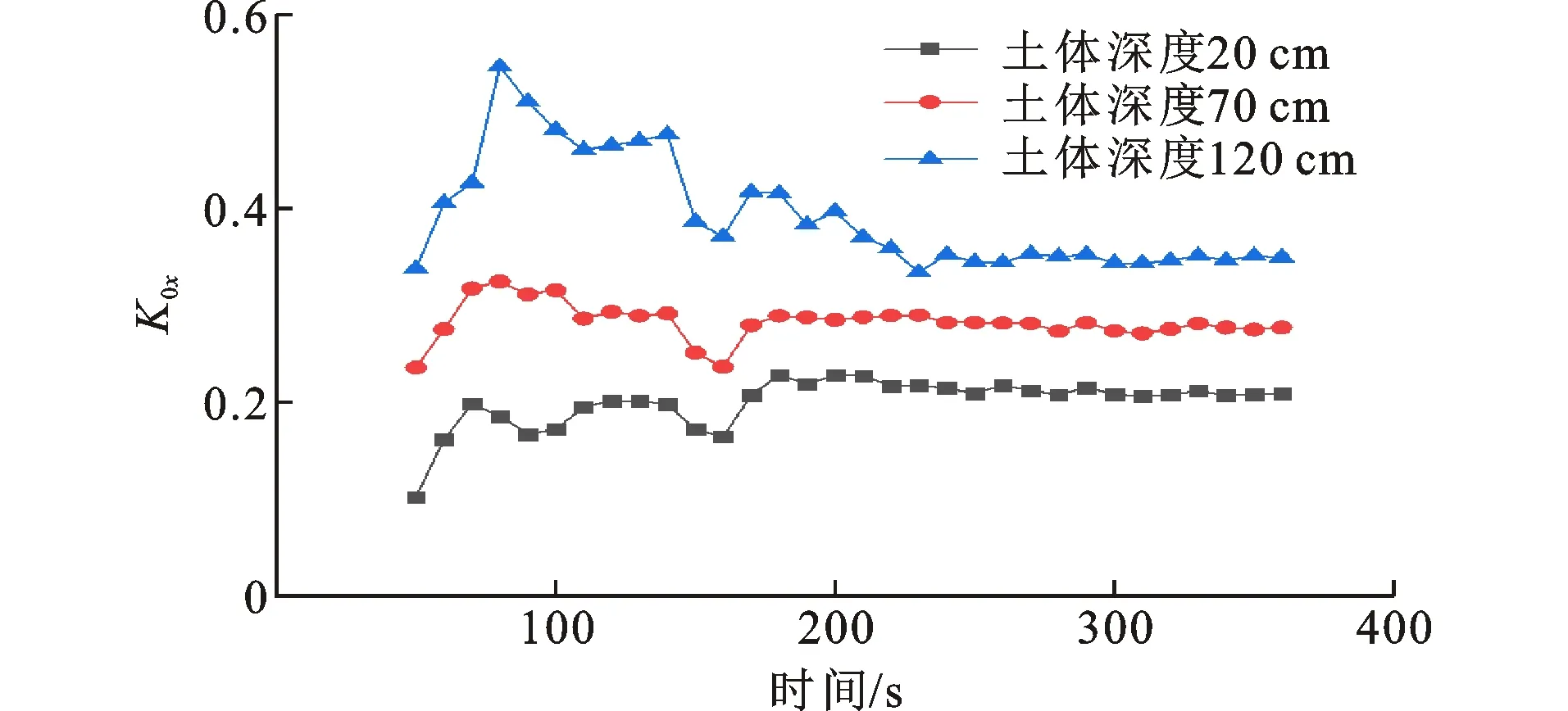
图11K0x随时间变化曲线Fig.11Change Curves of K0x with Time

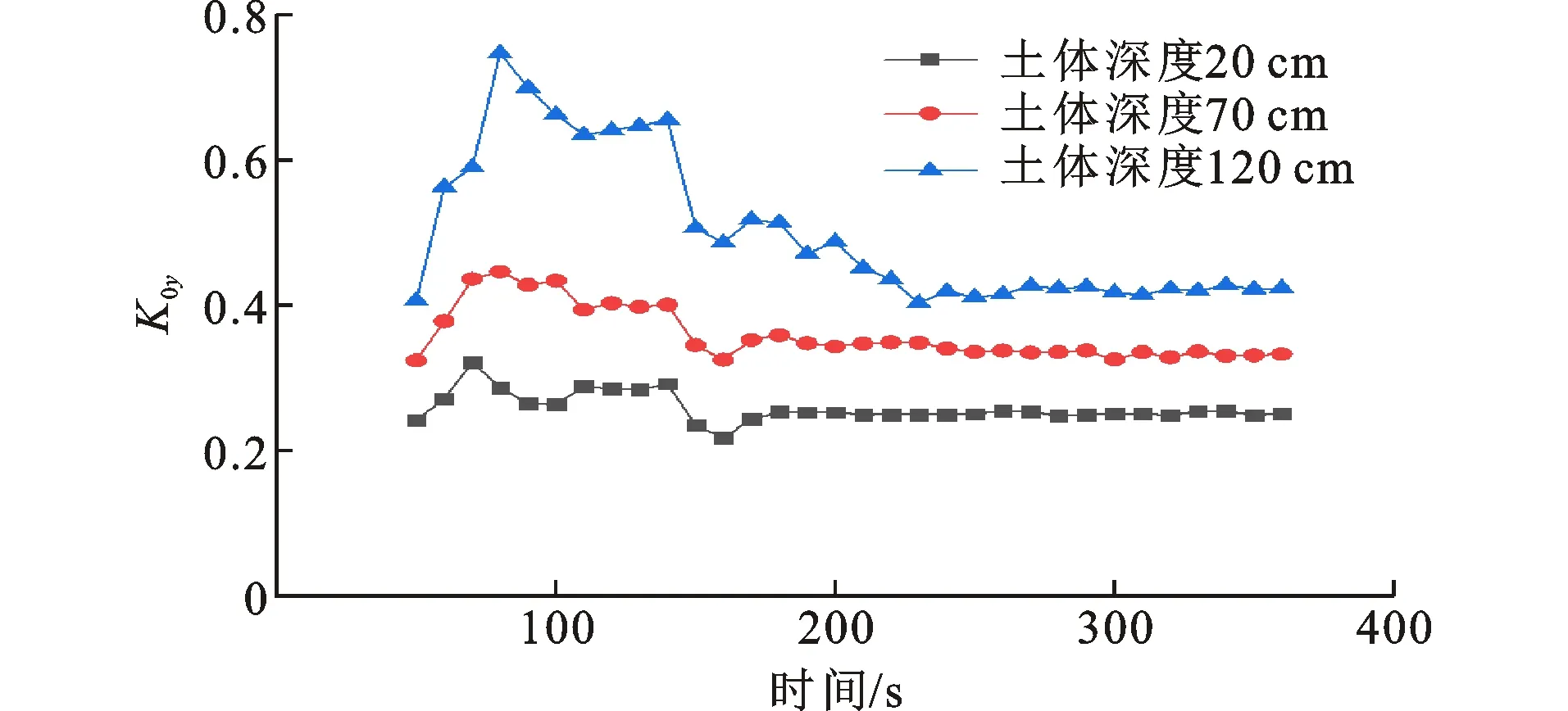
图12K0y随时间变化曲线Fig.12Change Curves of K0y with Time

对比图11、12可知，两曲线整体趋势基本一致，且卸载阶段都有明显的下降。区别在于不同深度土体的K0x值在每个时刻均小于K0y值，结合表1可以发现两者数值相差不大，而根据轴对称受力条件，两者理论上应是相等的。这主要和三维土压力盒的尺寸效应、土体的各向异性以及混凝土盖板的变形特点有关。土体深度为120 cm处K0x值接近经验值0.33～0.43[18]，K0y值满足《建筑地基基础设计规范》要求的0.4～0.5[19]。不同深度处土体K0x与K0y值相差也不大，其差值接近0，且均在0.04～0.07范围内，说明通过三维土压力盒测得的K0值真实有效。下面将从荷载传递与力系平衡、加卸载、主应力大小及方向、与传统经验方法对比以及突变5个方面对K0值变化进行分析。

表1不同深度处土体的K0稳定值范围Table 1K0 Stability Value Range of Soil at Different Depths

2.2.1 荷载传递与力系平衡分析

千斤顶施加的集中荷载通过混凝土盖板转化成为圆形均布荷载，该荷载作用在圆心处的土单元时，一部分主要变成土体受到的竖向应力，另一部分则变成水平向应力。随着土体深度的增加，荷载通过土体传递，逐渐转变为土体与筒壁间的摩擦力和土体相互接触的粒间应力，因此竖向应力和水平向应力逐渐减小。由于土单元竖直向受到的圆形均布荷载仍有一小部分存在，导致竖向应力减小的变化值大于水平向应力减小的变化值，从而使两者比值逐渐增大，根据式(2)，测点的静止侧压力系数K0也逐渐增大。最后，圆形均布荷载全部变成土体对底板的压力、土体与侧壁的摩擦力以及钢筋所受的拉力，故土体深度为20、70 cm的K0变化曲线波动较120 cm稳定些。

2.2.2 加卸载分析

从图11、12以及表1可以发现，在加卸载条件下，土体深度分别为20、70、120 cm的K0值随测试时间变化的整体趋势基本一致，即先增大再减小后趋于平稳。就y方向而言，相对第50 s，K0y值在加载末期均变大，这是由于荷载的增加使土体越来越密实。在110～140 s的加载过程中，K0y前后变化不大，K0x亦是如此，说明随着静止土压力的增大，筒内填土不再沉降。卸载后，土体K0变化曲线从明显下降到逐渐平缓，其中70 cm和120 cm处K0值从180 s起先减小再趋于稳定，原因在于卸载条件下深度越深，土体的回弹特征越明显。

2.2.3 主应力大小及方向分析

文献[20]中室内试验测试结果表明静止侧压力系数值随着主应力值增加而减小，非线性特征明显；原位测量结果表明K0值整体随着主应力σ1的增加而非线性减小。式(3)为计算应力空间中任意点的主应力大小及方向的三元一次方程组[21]。

(3)

式中：g、h、t为空间某点任一斜面外法线的方向余弦，且g2+h2+t2=1。

在稳定阶段，3个剪应力大小近似为0。另外，由于圆筒模型为轴对称实体，根据轴对称受力条件得到τxy=τyx，τyz=τzy，τzx=τxz。将这些关系代入式(3)得

(4)

由于g、h、t不能同时为0，从大小是否相等和方向是否一致可得到σx=σ或σy=σ或σz=σ。根据试验结果，σx、σy、σz均随着土体深度的增加而减小，结合文献[20]，最终得到在其他因素不变情况下，稳定后的静止侧压力系数K0随着土体深度的增加而增大。

2.2.4 与传统经验方法对比分析

三轴压缩试验采用低摩擦三轴测试仪，试验设备如图13(a)所示。取圆筒试样800 g，根据土工试验标准进行试验，其中围压依次设置为100、200、300、400 kPa，且每次围压对应的土样密度相等。试验结果如图13(b)所示的莫尔破坏包线，其中“σ=0.719 2τ+13.16”为库仑强度线方程。由此计算得到圆筒所用砂土的静止侧压力系数K0值为0.416，结合表1，该值处于圆筒模型试验测得的K0稳定值范围，这说明测算静止侧压力系数的圆筒模型试验可以用于新型土工试验。

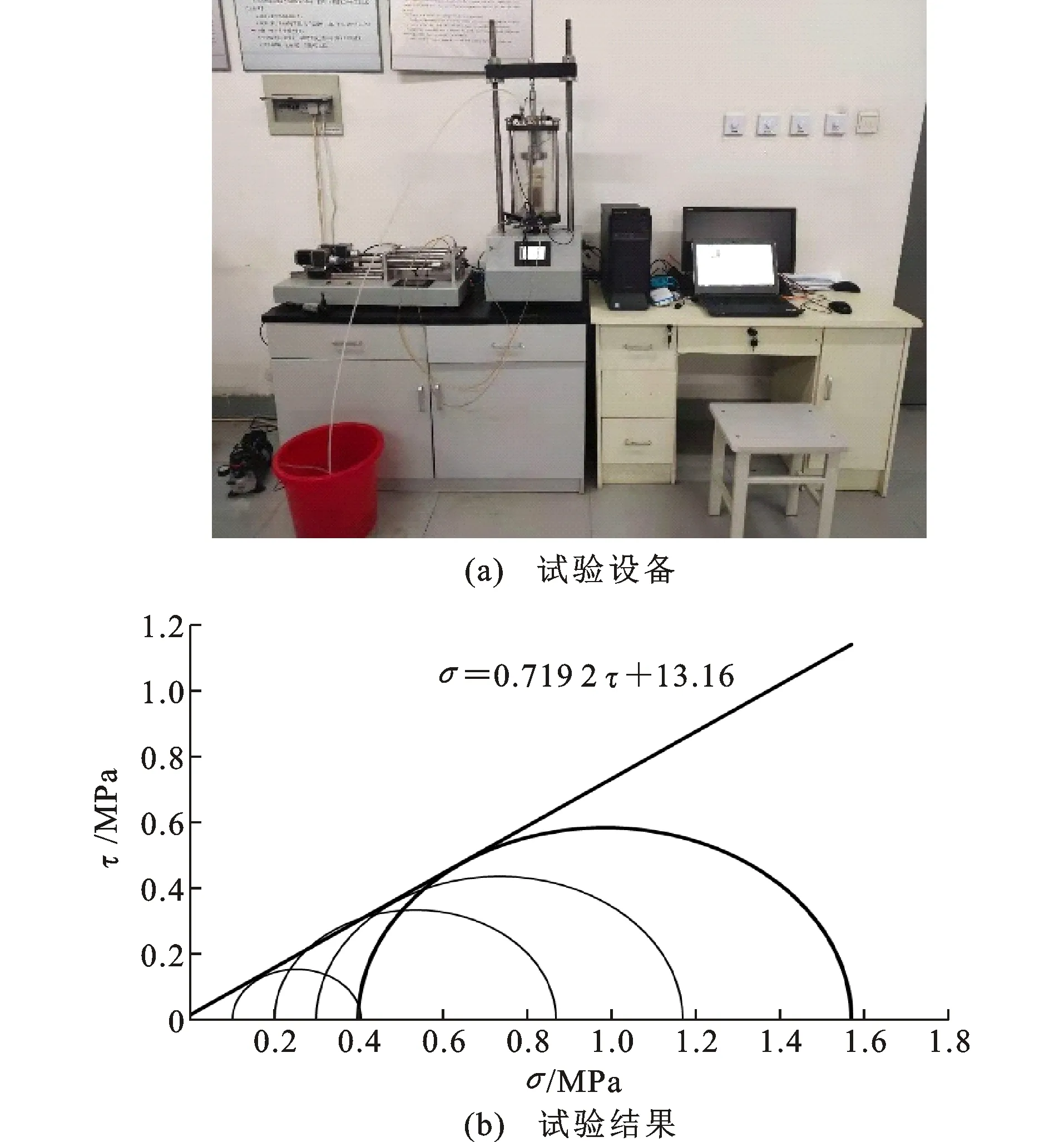
图13三轴压缩试验设备及结果Fig.13Triaxial Compression Test Equipments and Results

图14K0突变曲线Fig.14K0 Mutation Curves

2.2.5 突变分析

图14为K0突变曲线，可以看出在加载阶段的前50 s内，静止侧压力系数发生突变。图14中不同深度的K0值小至接近0，大至接近3，且水平直线K0=1以下的数据点较多。从三维应力状态的角度出发，3个正应力虽然变化不大，但存在竖向应力小于水平向应力的情况；从圆筒模型试验装置来看，初期加载过程中受力钢筋没有完全受拉，土体内部也没有达到三轴压缩试验应有的密实度。事实上，根据蒋明杰等[7]对静止侧压力系数的研究，试验整个压缩过程中K0值从突变到正常变化是合理的。

综合以上分析，圆筒模型试验所用砂土经过加载、卸载和稳定，其K0值受到深度的影响，圆筒内测点越深，砂土K0值越大并单调递增。在圆筒模型的基础上，若适当增加筒高和直径，而土类不变，预计砂土的K0值沿超过120 cm的一定深度内会继续增大，可能接近1，但随深度增加而变化的曲线的斜率会减小至0。

3结语

(1)制作了一种能够测算K0的圆筒模型试验装置，采用三维应力测试方法对浅层砂土进行加载和卸载，不同深度的正应力σx、σy、σz均随测试时间先增大再减小后平稳，说明该装置合理可行，该方法科学可靠。

(2)不同深度处的K0值变化趋势基本一致，并且随深度增加而增大。同一深度处水平方向K0x和K0y稳定后的差值在0.04～0.07之间。若减小三维土压力盒的角度旋转误差，并降低其尺寸效应，该差值会更接近0。