部分包覆钢-轻骨料混凝土组合短柱轴压性能数值分析

张慧洁，胡 晨，王静峰，钱正昊，刘 用

(1. 国网安徽省电力有限公司经济技术研究院，安徽合肥 230061； 2. 合肥工业大学土木与水利工程学院，安徽合肥 230009； 3. 合肥工业大学先进钢结构技术与产业化安徽省协同创新中心，安徽合肥 230009)

0引 言

在国家“碳达峰，碳中和”的可持续发展目标指导下，装配式建筑因其高效、环保等优势成为了建筑行业发展的新风向标[1]。部分包覆钢-混凝土组合(PEC)柱是一种在H型钢的翼缘与腹部间填充混凝土的新型组合结构柱[2-3]。PEC柱在具备优良性能的同时，可以较高程度实现结构构件的预制化与装配化，因此其在装配式建筑中具有广泛的应用前景。目前，国内外对PEC柱受力性能的研究初具成果[4-8]，并已成功应用在绍兴市行政中心配套住宅、盘锦市实验小学等实际工程中。

目前采用普通混凝土的装配式PEC部件因自重较大，存在着运输过程成本消耗大、装配过程施工难度高等问题，有悖于装配式建筑设计合理化、施工人性化的初衷。另一方面，轻骨料混凝土是一种干表观密度小于1 950 kg·m-3的新型绿色混凝土材料[9-10]，在保证强度的同时又能降低构件自重，与装配式建筑的发展理念不谋而合[11]。因此，将轻骨料混凝土应用在装配式构件中具有较高的研究意义与工程应用价值。

本文拟将轻骨料混凝土应用在PEC构件中形成部分包覆钢-轻骨料混凝土组合(PELC)短柱。然而，现有轻骨料混凝土构件的研究主要集中在钢筋轻骨料混凝土构件以及钢管轻骨料混凝土构件[12-17]，对部分包覆钢-轻骨料混凝土组合构件的研究尚未见报道。考虑到轻骨料混凝土与普通混凝土材料性能的差异，PELC构件和PEC构件中钢材和混凝土的相互作用机理并不完全相同，因此有必要对PELC构件的受力性能展开深入研究与分析。

本文将对轴压荷载作用下的PELC短柱受力性能进行研究。首先通过ABAQUS软件建立轴压荷载下PELC短柱的有限元模型，开展PELC短柱的全过程受力分析，揭示PELC短柱在不同阶段的应力发展过程以及典型破坏模式，在此基础上研究不同参数对PELC短柱轴压性能的影响规律。最后，基于规范AISC 360[18]以及轻骨料混凝土约束本构提出了一种能够预测PELC短柱的轴心承载力的计算公式。PELC短柱的截面如图1所示，本文研究成果拟为部分包裹轻骨料混凝土组合柱在实际工程中的应用提供理论依据。

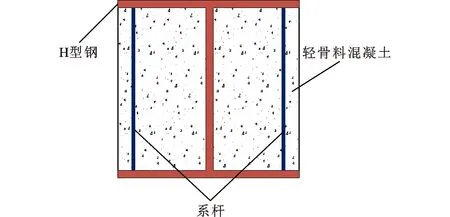
图1PELC短柱截面Fig.1Section of PELC Stub Column

1数值分析模型

1.1材料模型

根据规范[19]要求，将轻骨料混凝土应用于PEC构件中时，须采用LC25以上的混凝土强度等级，属于高强轻骨料混凝土。对于高强轻骨料混凝土，宜采用文献[20]提出的轻骨料混凝土应力-应变(σ-ε)曲线，数学表达式为

(1)

式中：σc为轻骨料混凝土压应力；fc为轻骨料混凝土轴心抗压强度标准值；εc为轻骨料混凝土峰值压应变；αa、αd1为和轻骨料混凝土等级相关的系数。

αa、αd1、εc的具体取值如表1所示。

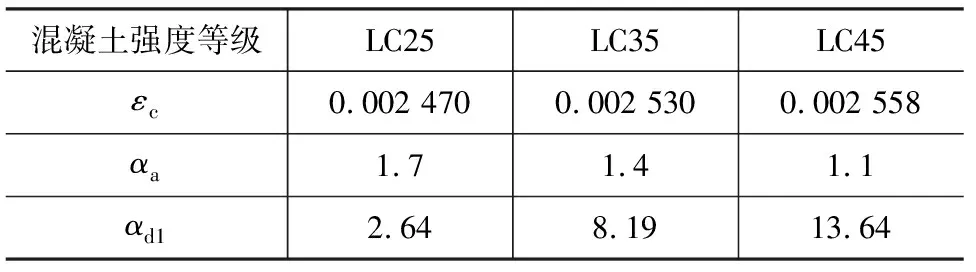
表1轻骨料混凝土应力-应变曲线系数Table 1Stress-strain Curve Coefficient of Lightweight Aggregate Concrete

轻骨料混凝土受拉本构关系模型参考文献[21]中提供的曲线进行计算，即

(2)

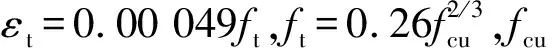
构件中系杆、H型钢以及端板均为钢材，其中系杆和端板采用简化的双折线模型。H型钢采用文献[22]建议的二次塑流模型，其应力-应变关系曲线如图2所示，其中，fb为钢材弹性阶段最大应力，fu为钢材的极限强度。具体表达式为

(3)

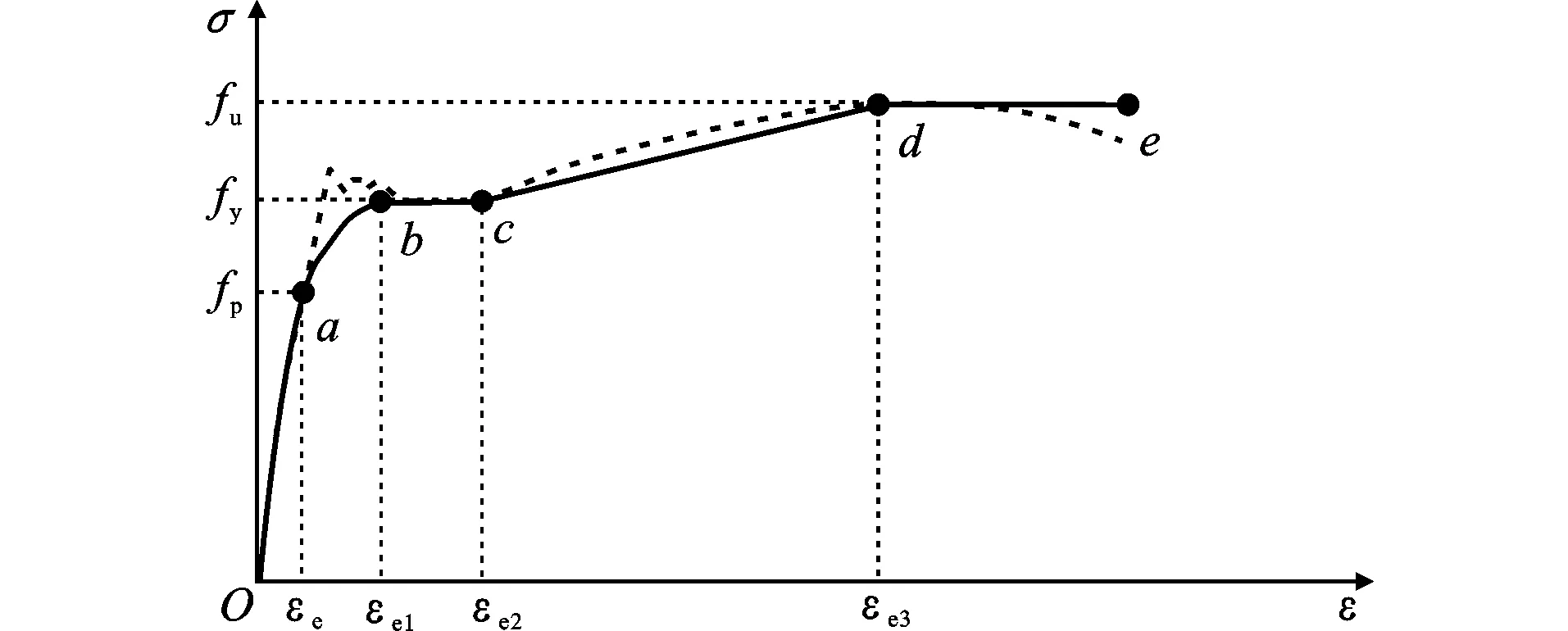
图2钢材应力-应变曲线Fig.2Stress-strain Curve of Steel

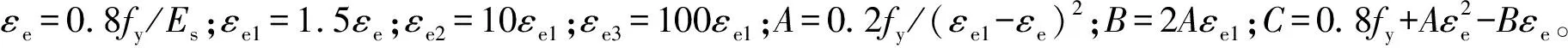
1.2有限元分析模型

本文建立的PELC短柱有限元模型尺寸为400 mm×400 mm×1 600 mm，构件的主要组成部分为端板、H型钢、轻骨料混凝土以及系杆。系杆采用三维桁架单元T3D2，其余部分均采用三维实体单元C3D8R。以标准试件PELC12-S200-35为例，端板、H型钢与轻骨料混凝土的网格尺寸为30 mm×30 mm，系杆的网格尺寸为20 mm×20 mm。PELC短柱有限元分析模型如图3所示。

图3PELC短柱有限元分析模型Fig.3Finite Element Analysis Model of PELC Stub Column

在PELC短柱有限元模型中，轻骨料混凝土与H型钢间的接触行为通过法向的“硬接触”与切向的“罚函数”进行模拟，其摩擦因数设置为0.6[23]。为简化分析模型，通过“Embedded”行为将系杆内置到整个模型中用来模拟杆与轻骨料混凝土、型钢间的复杂接触行为。同时，由于端板与H型钢是通过焊接连接的，不发生相对滑移，因此采用“Tie”绑定进行模拟。端板与端部轻骨料混凝土的法向行为为“硬接触”，切向行为的摩擦因数为0.4。为保证轴向荷载竖直作用在构件上，通过在端板中部的刀铰中部施加位移进行加载。同时，约束上端板处X、Y方向的平动以及Z方向的转动，下端板处约束X、Y、Z方向的平动。

2试验验证

目前国内外尚缺乏部分包覆钢-轻骨料混凝土组合构件的力学性能试验研究。因此，本文选取文献[24]中薄壁钢管轻骨料混凝土柱偏压试验和文献[25]中PEC柱轴压试验进行数值分析验证，从而确保轻骨料混凝土本构关系曲线的准确性与PEC柱有限元模型的合理性。对构件的荷载-位移(N-Δ)曲线以及典型破坏模式进行对比，如图4～6所示。

图4薄壁圆钢管轻骨料混凝土柱偏压试验曲线与计算曲线比较Fig.4Comparison of Eccentric Compression Test and Calculation Curves of Lightweight Aggregate Concrete Column with Thin Wall Round Steel Tube

图5部分包覆钢-混凝土组合柱轴压试验曲线与计算曲线比较Fig.5Comparison of Axial Compression Test and Calculation Curves of Partially-encased Concrete Composite Column

图6试验与有限元典型破坏模式对比Fig.6Comparison of Typical Failure Modes Between Test and Finite Element Model

对比结果表明：有限元分析模型计算曲线与试验曲线的整体误差较小；有限元计算与试验的典型破坏模式较为吻合。因此，本文建立的PEC结构模型与轻骨料混凝土材料模型可为部分包覆钢-轻骨料混凝土组合(PELC)短柱的轴压性能分析奠定了基础。

3PEC与PELC短柱轴压性能对比

为探究普通混凝土与轻骨料混凝土对部分包覆钢-混凝土组合短柱的影响，本节将采用标准模型分别建立PEC与PELC短柱模型，混凝土强度均取35 MPa，普通混凝土本构模型的选用根据规范[26]确定。标准试件尺寸的信息如下：截面长度为400 mm，宽度为400 mm，柱长为1 600 mm。H型钢的腹板厚度为10 mm，翼缘厚度为12 mm，系杆直径为12 mm，系杆间距为200 mm。H型钢屈服强度为355 MPa，系杆选用强度等级为HRB400的钢筋。

PEC与PELC短柱的荷载-位移曲线对比如图7所示。由图7可知，与PEC短柱相比，PELC短柱的峰值位移有着较大的提高，这是由于轻骨料混凝土的峰值应变更大引起的。轻骨料混凝土脆性破坏特性相比于普通混凝土更加明显，这造成了PELC短柱的峰值荷载与极限荷载均有一定程度降低。对比结果表明，采用轻骨料混凝土的PEC构件中H型钢性能将得到更好地利用，更能发挥组合结构钢与混凝土结构协同受力的独特优势。

图7PEC与PELC短柱荷载-位移曲线对比Fig.7Comparison of Load-displacement Curves Between PEC and PELC Stub Columns

4典型试件全过程受力分析

为探究部分包覆钢-轻骨料混凝土组合短柱在轴压荷载作用下的受力机理，本节以标准试件PELC12-S200-35为例，建立部分包覆钢-混凝土组合短柱的有限元数值分析模型，并对PELC短柱的N-Δ曲线展开全过程受力分析。PELC短柱的N-Δ曲线(图8)按线段特征可大致分为3个阶段：弹性阶段(OM段)、弹塑性阶段(MN′段)以及下降阶段(N′P段)。在此基础上，对曲线不同特征的应力展开分析，其中轻骨料混凝土选用纵向平均应力，型钢及系杆选用Mises应力。为了更好地分析PELC短柱在各阶段的受力特点，本节将PELC短柱的变形进行了放大，放大系数为8，试件PELC12-S200-35的特征点应力云图如图9所示。

图8轴压荷载作用下PELC短柱的典型轴向

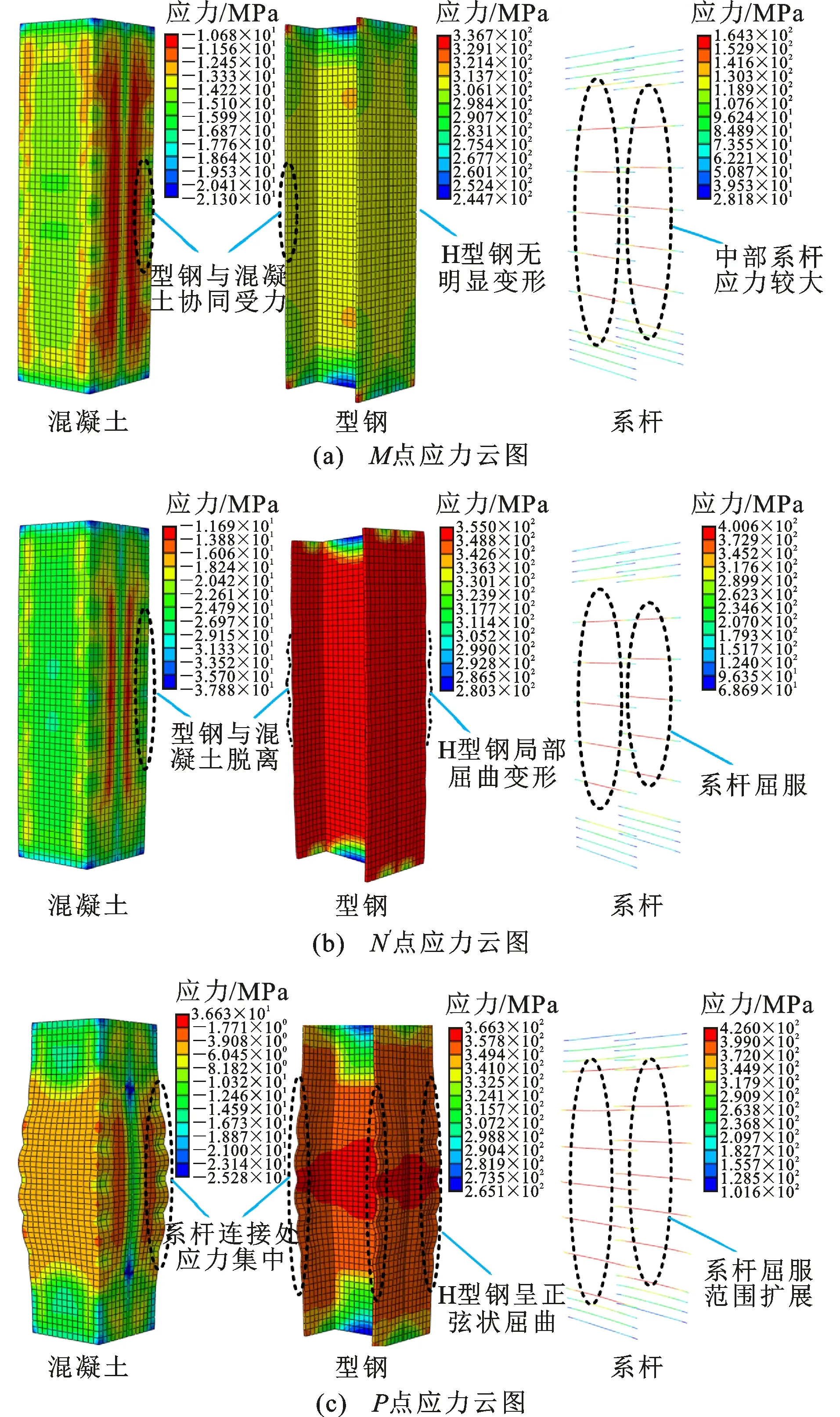
图9试件PELC12-S200-35的特征点应力云图Fig.9Stress Nephogram at Characteristic Points of Specimen PELC12-S200-35

(1)弹性阶段(OM段)：构件各组成部分基本处于弹性状态，构件的N-Δ曲线处于线性增长状态。

曲线达到M点时，试件各组成部分的应力发展情况如图9(a)所示。此时，轻骨料混凝土的应力未充分发展，但由于受到系杆的拉结作用，系杆周围的轻骨料混凝土产生较大的应力。同时，H型钢应力有了一定的发展，但尚未屈服。另一方面，H型钢与轻骨料混凝土均未产生较大变形，两者可以较好地协同变形。系杆的应力发展较慢，其最大应力分布在与混凝土最大应力相对处的中部区域。

(2)弹塑性阶段(MN′段)：随着荷载的持续增加，构件各组成部分均有了一定的塑性发展。构件的N-Δ曲线呈现非线性发展状态。此阶段，H型钢应力逐渐增长至屈服。轻骨料混凝土受压膨胀，但其横向变形受到H型钢翼缘与系杆的约束。系杆将发挥拉结作用，应力快速增长。

曲线到达N′点时，试件各组成部分的应力发展情况如图9(b)所示。此时，构件中的大部分轻骨料混凝土已经到达峰值应力。H型钢主体部分已经屈服，且腹板由于轻骨料混凝土的包裹作用并未产 生明显的变形，但翼缘部分由于系杆的拉结作用出现了局部屈曲变形现象，导致了轻骨料混凝土与型钢间出现了一定的分离。系杆中部的应力已经达到屈服强度。

(3)下降阶段(N′P段)：峰值点后，轻骨料混凝土的应力处于下降段，H型钢与系杆渐渐进入强化阶段。此阶段轻骨料混凝土的应力不断下降。系杆与H型钢的应力小幅度增加，但变形不断增长。

曲线到达P点时，试件各组成部分的应力发展情况如图9(c)所示。此时，中部轻骨料混凝土产生了严重的鼓曲变形，应力大幅度下降，表明轻骨料混凝土基本退出工作。受到系杆拉结作用的影响，H型钢外翼缘呈现正弦半波状鼓曲。系杆屈服的范围由非加密区扩张到了加密区，系杆的横向伸长量较大，处于强化阶段。

5参数分析

为研究轴压荷载下部分包覆钢-轻骨料混凝土组合短柱的受力性能，本文对轻骨料混凝土强度、系杆间距、含钢率以及截面形状等参数影响下PELC短柱的受力性能展开了深度分析。各试件的尺寸信息、峰值承载力以及延性如表2所示，轴向荷载-位移(N-Δ)曲线如图10所示。延性系数γ的定义如式(4)所示。

(4)

式中：Δu为构件峰值承载力对应的竖向位移；Δ85%为轴向荷载降至85%峰值承载力时对应的竖向位移。

(1)轻骨料混凝土强度。表2与图10(a)分别给出了轻骨料混凝土强度为LC25、LC35、LC45对 应的PELC短柱在轴压荷载作用下的峰值承载力、延性系数和N-Δ曲线。与轻骨料混凝土强度等级为LC25的PELC短柱相比，轻骨料混凝土强度为LC35和LC45的试件峰值承载力分别提高了12.73%和24.60%。延性系数分别降低了8.33%和12.88%。结果表明，随着轻骨料混凝土强度的增加，PELC短柱的峰值承载力将不断增长，延性会逐渐降低。这是由于轻骨料混凝土强度越高，变形能力越差。

表2部分包覆钢-轻骨料混凝土组合短柱有限元计算参数Table 2Finite Element Calculation Parameters of Partially-encased Lightweight Aggregate Concrete Composite Stub Columns

图10轴压荷载下部分包覆钢-轻骨料混凝土组合短柱轴向荷载-位移曲线Fig.10Axial Load-displacement Curves of Partially-encased Lightweight Aggregate Concrete Composite Stub Columns

(2)系杆间距。表2与图10(b)分别给出了系杆间距为100、200、400 mm对应的PELC短柱在轴压荷载作用下的峰值承载力、延性系数和N-Δ曲线。与系杆间距为100 mm的PELC短柱相比，系杆间距为200 mm和400 mm的试件峰值承载力分别降低了0.63%和1.38%。延性系数分别降低了1.65%和3.25%。在本文限定的范围内，PELC短柱的峰值承载力与延性会随着系杆间距的减小渐渐增加。从第2节的分析可知，系杆的拉结作用能延缓H型钢的鼓曲变形，可以有效提高PELC短柱的延性。另一方面，系杆不参与PELC短柱的截面承载力计算，但系杆与H型钢的套箍作用能约束轻骨料混凝土的变形，能够小幅度提高PELC短柱的峰值承载力。

(3)含钢率。表2与图10(c)分别给出了含钢率为8.35%、9.33%、10.30%对应的PELC短柱 在轴压荷载作用下的峰值承载力、延性系数和N-Δ曲线。与含钢率为8.35%的PELC短柱相比，含钢率为9.33%和10.30%的试件峰值承载力分别提高了6.28%和12.78%。延性系数分别增长了0.83%和1.65%。结果表明，随着含钢率的增加，PELC短柱的峰值承载力将会增加，延性会有略微的提升。这是由于含钢率的增大将降低轻骨料混凝土的用量，PELC短柱的峰值承载力与延性将有一定的提升。

(4)翼缘宽厚比。考虑到轻骨料混凝土的强度可能与翼缘的约束效应有关，本节在含钢率和截面面积不变的情况下探索翼缘宽厚比对PELC短柱轴压性能的影响。表2与图10(d)分别给出了翼缘宽厚比为33.33、31.79、41.67对应的PELC短柱在轴压荷载作用下的峰值承载力、延性系数和N-Δ曲线。与翼缘宽厚比为33.33的PELC短柱相比，翼缘宽厚比为31.79和41.67的试件峰值承载力分别降低了0.29%和0.51%。延性系数无明显变化。因此，在本文分析的常用参数范围内，可忽略翼缘宽厚比对PELC短柱的轴压性能的影响。

6PELC短柱轴压承载力计算公式

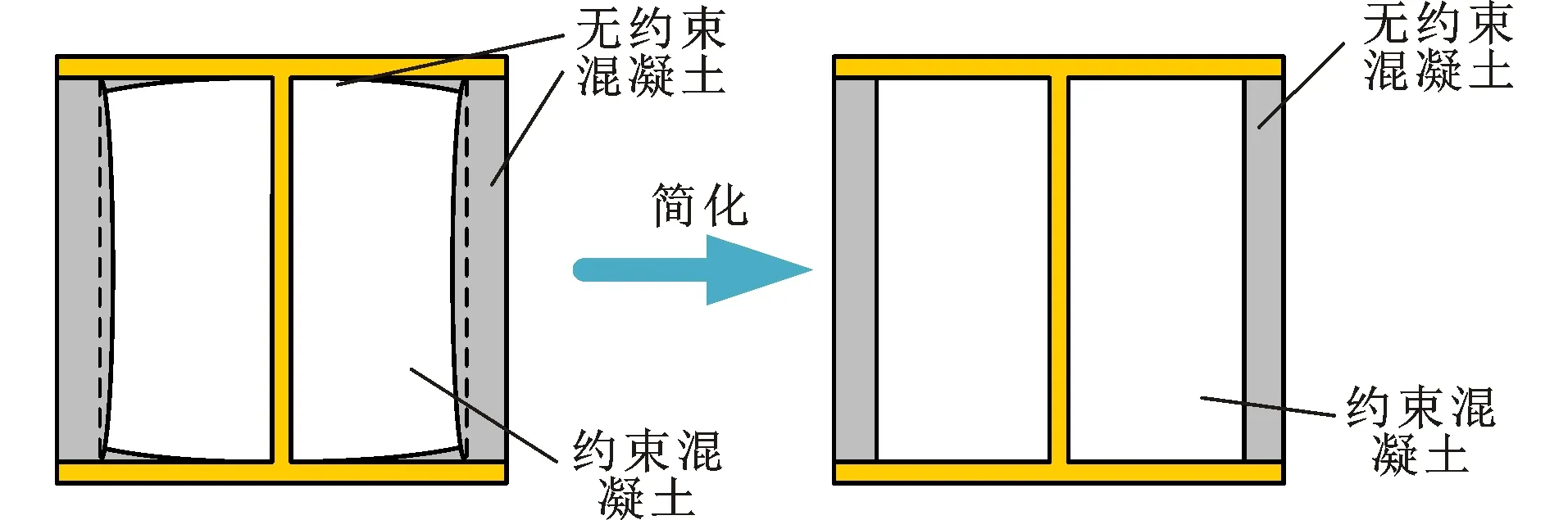
图11PELC短柱混凝土截面区域划分Fig.11PELC Stub Column Concrete Section Area Division

根据前文分析可知，系杆与H型钢的联合作用能够起到类似箍筋的约束效应，提高轻骨料混凝土的强度。因此，本节将根据规范AISC 360[18]中有关部分包覆钢-混凝土组合短柱的计算规定对PELC短柱的轴压承载力进行预测。图11(a)为考虑了腹板、翼缘以及系杆约束作用后的PELC短柱截面混凝土约束。为方便计算，本文将混凝土近似简化划分为图11(b)所示无约束混凝土与约束混凝土2个区域。约束区采用Khaloo等[27]提出的轻骨料混凝土约束模型进行计算，无约束区采用素混凝土强度进行计算，则PELC轴压承载力Nuc可由式(5)计算。

Nuc=fyAy+0.85(fccAcc+fcoAco)

(5)

式中：Ay为H型钢的截面面积；fcc和Acc分别为受约束混凝土的圆柱体轴心抗压强度及截面面积；fco和Aco分别为无约束混凝土的圆柱体轴心抗压强度及截面面积。

Khaloo等[27]提出的受约束轻骨料混凝土抗压强度可由式(6)～(8)计算。

(6)

(7)

[h-0.5s′tan(θ)]/(wh)

(8)

式中：fle为有效侧向约束力；fhcc为峰值点处箍筋实际应力，取为箍筋屈服强度；ke为有效约束系数；Ast为系杆截面面积；h为H型钢半截面净高；w为系杆至H型钢腹板的距离；s′为系杆净距；α和θ分别为约束曲线常数及角度，根据文献[28]分别取为6.5及45°。

为验证计算公式的适用性与准确性，将公式计算的承载力与有限元模拟的结果进行比较，结果如表3所示。对比发现，公式计算结果与有限元模拟数据比值的平均值为1.016，标准差为0.005 0。对比结果表明，本节提出的计算公式能够精确且保守地预测PELC短柱的轴压承载力。综上所述，本文提出的计算公式具有一定的安全储备，能够为PELC柱在实际工程的应用提供理论基础。

7结语

(1)本文建立了部分包覆钢-轻骨料混凝土组合短柱在轴压荷载作用下的有限元模型，并通过已有试验结果对模型的正确性以及轻骨料混凝土本构模型的适用性进行了验证。结果表明该有限元模型与实际情况具有较好的吻合度，能够用于轴压荷载下PELC短柱的计算与分析。

表3PELC短柱轴压承载力对比Table 3Comparison of PELC Stub Column Axial Compression Bearing Capacity

(2)PELC短柱在轴压荷载作用下的全过程受力曲线可分为弹性阶段、弹塑性阶段以及下降阶段3个阶段。PELC短柱的最终破坏形式为构件中部的轻骨料混凝土鼓曲破坏，H型钢屈服且外翼缘呈现正弦半波状鼓曲，系杆被拉长且进入强化阶段。

(3)提高PELC短柱的含钢率对其峰值承载力有较大的影响，但是对其延性的影响较小；提高轻骨料混凝土强度对其峰值承载力及延性均有较大的影响；另外，在本文分析的常用参数范围内改变系杆间距和翼缘宽厚比对PELC短柱峰值承载力和延性的影响较小。

(4)本文基于规范AISC 360以及轻骨料混凝土箍筋约束模型提出了部分包覆钢-轻骨料混凝土组合短柱轴压承载力计算公式。计算结果与数值分析结果吻合较好，可为部分包覆钢-轻骨料混凝土组合短柱的实际应用提供理论指导。