海洋环境荷载下半潜式平台上承房屋钢框架结构的动力响应特征
李富民,刘永强,赵 婕,郭 震
(中国矿业大学江苏省土木工程环境灾变与结构可靠性重点实验室,江苏徐州 221008)
0引 言
随着陆地资源逐渐减少,人们将目光投向了更为广阔的海洋空间,各类海洋开发平台正在快速发展。半潜式平台因其水线面小、载重量大的优点成为了目前国内外海洋开发的主流平台,主要应用于深海资源勘探、油气生产加工以及火箭发射等业务[1]。同时,为了解决人工吹填建岛带来的严重环境破坏问题以及只适宜于近海建造的条件限制问题,采用半潜式平台代替人工吹填建岛模式也将成为未来的发展趋势[2]。因此,半潜式平台的使用功能将不断增多,从业人员数量也将不断增加,平台上承生产、生活用房的需求必将日益增多,上承房屋结构的海洋环境荷载动力响应分析及设计方法研究工作亟需开展。
既有关于半潜式平台结构的研究工作主要体现在以下两个方面:
(1)关于平台自身整体结构极限强度的研究。冯国庆等[3-4]采用直接计算法对平台结构的总强度进行评估,通过三维水动力理论和设计波法计算了结构在多种工况下的应力响应,对平台结构总强度进行了校核,并给出了半潜式平台的设计建议。白艳彬等[5]针对平台结构总体强度分析,提出了计算工况选取原则及控制总体强度的关键因素。Jang等[6]采用有限元方法对半潜式结构的重量优化进行研究,开发了一套内部强度评估系统,根据结构的屈曲强度对半潜式结构进行优化,实现了半潜式结构强度评估过程的全自动化。叶谦等[7]基于半潜式平台结构整体强度分析方法,采用非线性逐步垮塌分析法建立了不同控制工况下极限承载力模型的功能函数,提出了串联结构体系可靠度计算方法。祁恩荣等[8]采用解析方法和简化方法对半潜式平台极限强度进行比较研究,建立了半潜式平台可靠性计算模型。张大勇等[9]提出了典型半潜式平台在海冰作用下的主要失效模式和评价方法。饶鑫等[10]通过对平台自身生活区横向、纵向布置的对比分析,得到了生活区参与平台总强度的规律。
(2)关于平台自身关键节点极限强度的研究。半潜式平台主体与浮体一般由加劲板结构组成,加劲板在焊接过程中会产生初始变形和残余应力,在结构承受荷载时造成不利影响。Paik等[11-13]通过试验和非线性有限元方法研究了考虑结构裂纹影响的板在轴向压缩或拉伸下的极限强度。Estefen等[14]研究了半潜式平台一个柱段中的加劲板在屈曲荷载及后屈曲条件下的状态,以及不同板缺陷情况对屈曲扩展的影响。Cheon等[15]对半潜式平台甲板底部加筋板在考虑流固耦合作用下的砰击压力进行研究。Huo等[16]提出了一种基于数值模型重建和外推的支撑结构强度分析方法,通过模型试验与数值模拟对考虑波浪冲击荷载的支撑强度进行研究。张健等[17]对深海半潜式平台典型构件和节点在腐蚀损伤下的极限强度进行研究,总结出腐蚀损伤对平台极限承载力的影响及随时间的演变规律。嵇春艳等[18-19]基于逐步破坏分析法和有限元计算方法,提出了一种考虑材料腐蚀、疲劳裂纹等结构损伤的半潜式海洋平台关键结构全寿期极限强度计算方法。
综上,既有半潜式平台结构的研究工作主要着眼于平台整体、关键节点的极限强度方面,而对于平台上承结构的有关问题研究较少[20]。本文基于深海半潜式平台上承房屋结构设计建造需求,选取较为适宜的钢框架结构为对象,对不同高度的钢框架结构进行极端海洋环境荷载作用下的动力时程分析;据此确定适宜的结构高度,然后对适宜结构高度进一步进行陆地8度设防地震和海洋3个等级环境荷载作用下的动力时程响应分析,通过对比得到海洋环境荷载作用下平台上承钢框架结构的动力响应特征,为海洋平台上承结构物的设计建造提供参考。由于海洋平台结构尺度非常大,真正有效的试验研究难度也就非常大,当前几乎所有此类研究都还只能采用数值模拟方法进行,因此,本文也将采用大型通用有限元分析软件ANSYS与水动力分析软件AQWA进行分析研究。
1海洋环境荷载下不同高度上承结构的动力响应模拟分析
在海洋环境荷载中,风荷载占有一定的比例,海面以上结构物高度对该比例的影响较大[21-22];另一方面,海洋平台的竖向稳固性相对较差,海洋环境荷载作用容易引起上下摇动,因而上承结构对自身的重心高度较为敏感。因此,研究海洋环境荷载作用下上承结构高度对其动力响应特征的影响,继而找出较为合适的高度作为推荐高度对于海洋平台上承结构设计非常必要。为此,本文建立3层、6层和9层(分别高9、18、27 m)3个平台上承钢框架结构模型进行动力响应有限元模拟研究,结构整体布置如图1所示。
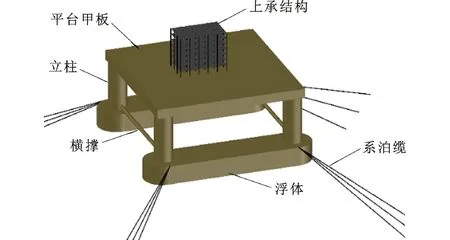
图1结构整体布置Fig.1Overall Layout of Structure
1.1结构参数
1.1.1 平台主体
半潜式平台主体采用常规四立柱双浮体形式。平台上部采用箱式甲板结构,水下采用双浮体结构,甲板与浮体之间采用四立柱进行连接,立柱相互之间通过横撑进行支撑[23]。各部分材料均采用Q345钢;平台主体自重25 000 t,主要几何参数如表1所示。
1.1.2 系泊系统
海洋平台工作的设计水深为1 000 m, 采用张紧式系泊系统设计方案,如图2所示。系泊系统共采用4组系泊缆沿浮体四角对称布置,每组系泊缆由3根等长的缆绳组成,每根缆绳与其水平投影的夹角均为40°,中间缆绳的水平投影与X(或Y)轴的夹角为45°,相邻两根缆绳之间的空间夹角为5°;每根缆绳的长度为1 490 m,预张力为1 000 kN,系泊缆材料组成及其性能参数如表2所示。

表1平台主体几何参数Table 1Geometric Parameters of Platform Body
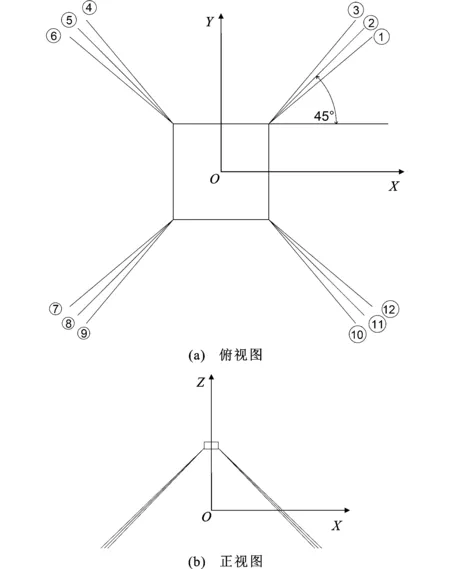
图2系泊系统布置Fig.2Mooring System Layout
1.1.3 上承结构
上承结构以住宅建筑为依据,按照陆地《钢结构设计标准》(GB 50017—2017)[24]《建筑抗震设计规范》(GB 50011—2010)[25]和《建筑结构荷载规范》(GB 50009—2012)[26]设计,截面参数如表3所示。本结构设定抗震类别为丙类,设防烈度为8度,场地类别为Ⅱ类,设计地震分组为第一组。
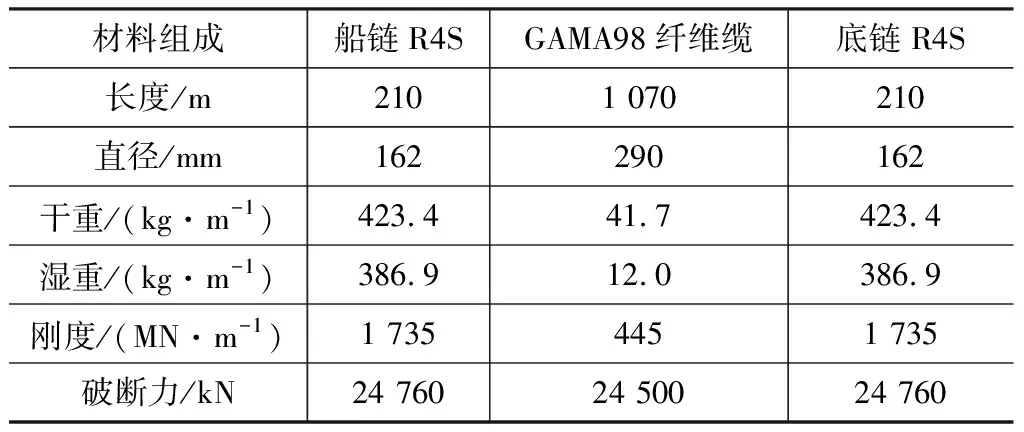
表2系泊缆材料组成及其性能参数Table 2Material Composition and Performance Parameters of Mooring Lines
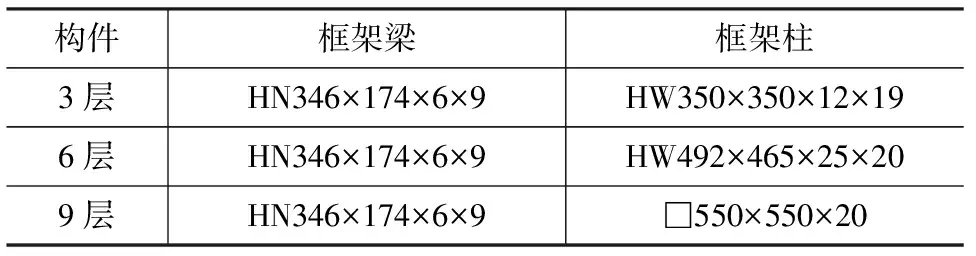
表3上承结构构件截面参数Table 3Section Parameters of Top Structure Members
3层、6层和9层钢框架(分别记为S3、S6和S9)的结构平面布置相同,如图3所示,每层的层高均为3 m。采用PKPM进行结构设计,3个结构所有框架梁的截面均取为相同,而框架柱的截面则按照3个结构各对应楼层层间位移角相近的原则确定;框架柱与框架梁的材料均采用Q345钢。所有楼板均采用100 mm厚压型钢板-混凝土组合板,其中压型钢板采用Q345的YX75-200-600开口型压型钢板,钢板厚度为0.75 mm;混凝土采用强度等级为C30的商品混凝土。所有墙体均采用尺寸为600 mm×200 mm×200 mm的蒸压加气混凝土砌块,并沿每层框架纵、横双向框架梁方向布置。3个结构的自重分别为620、1 278、2 007 t。
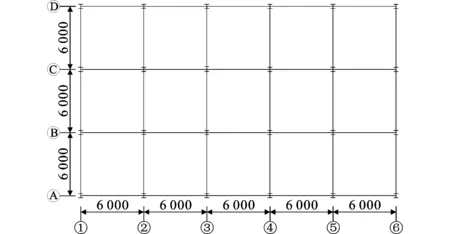
图3上承钢框架结构平面布置(单位:mm)Fig.3Plan Layout of Steel Frame Top Structure (Unit:mm)
1.2有限元模型
在ANSYS中建立结构有限元分析模型。平台主体由甲板、立柱与浮体组成,平台浮体、甲板与立柱均采用Shell181单元,横撑采用Pipe59单元。平台水动力计算模型如图4所示。
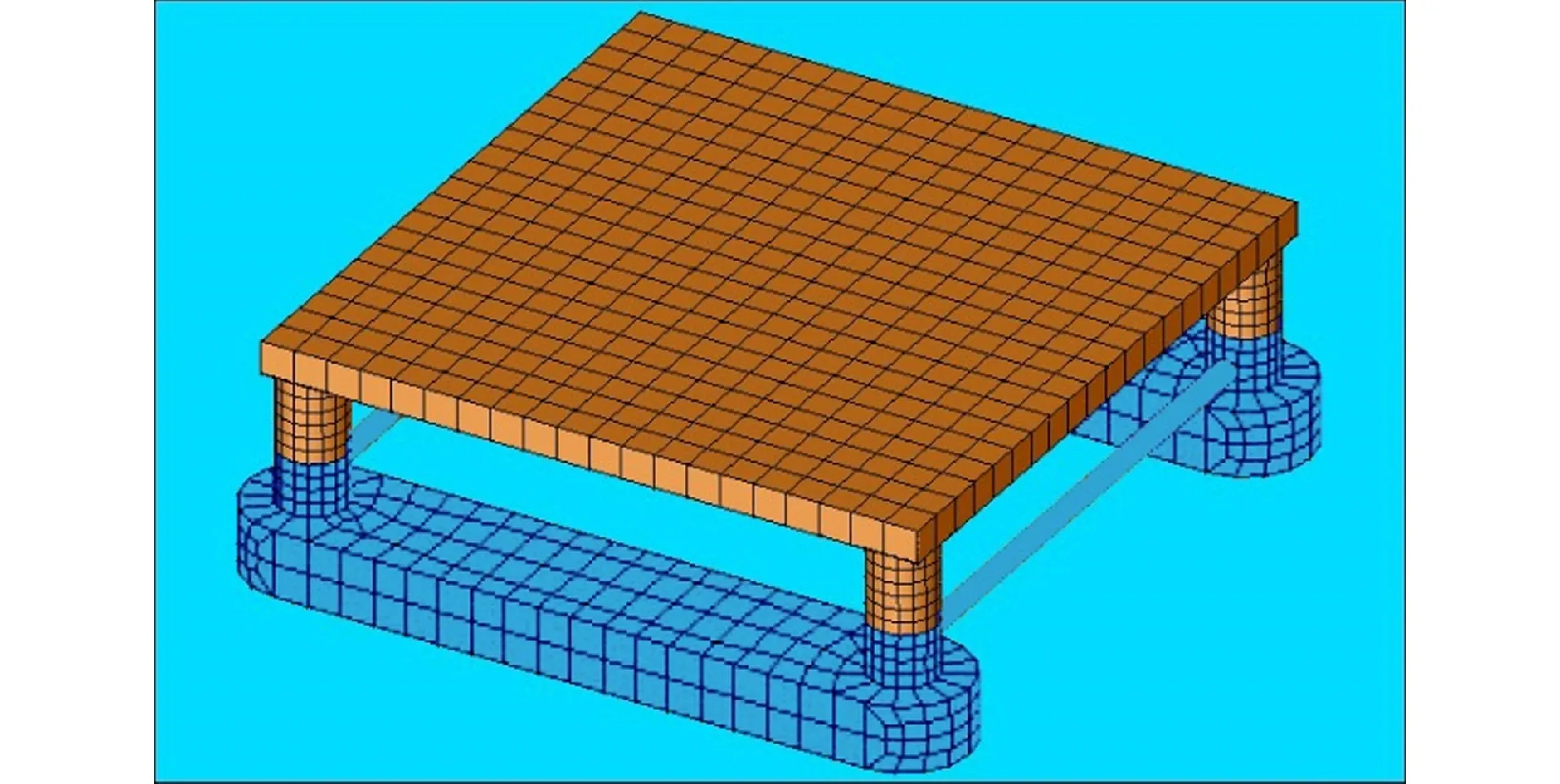
图4平台水动力计算有限元模型Fig.4Finite Element Model for Hydrodynamic Calculation of Platform
平台上承结构的框架柱与框架梁选用Beam188单元,板采用Shell181单元。框架梁与框架柱、楼板与框架梁之间均采用刚接形式连接。上承结构有限元分析模型如图5所示(以6层框架为例)。

图5上承结构动力响应分析有限元模型Fig.5Finite Element Model for Dynamic Response Analysis of Top Structure
1.3荷载选取
平台设计工作水深为1 000 m,海水密度为1 025 kg·m-3,空气密度为1.29 kg·m-3,重力加速度为9.81 m·s-2。波浪谱采用JONSWAP谱,风谱采用NPD谱,流荷载采用流速的方式进行施加。根据南海波浪分布图选取100年一遇的极端海况提取海洋环境荷载,具体环境荷载参数见表4。根据此荷载,采用波浪、风、流同向的最不利组合工况,在AQWA中对平台进行水动力计算,获取每个立柱与海平面交界线的2个外侧顶点(4根柱共8个点)的位移时程曲线,进一步在ANSYS中将上述8条位移时程曲线作为荷载施加到4个立柱的8个点上,对平台进行瞬态动力学分析。
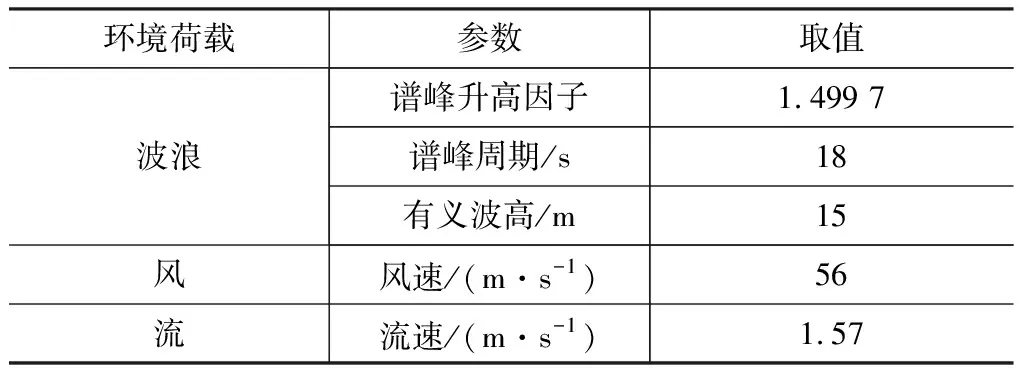
表4100年一遇极端海况参数Table 4Extreme Sea State Parameters with 100 Year Return Period
1.4动力时程分析
由于平台甲板的整体刚度很大,对上承结构的动力响应影响仅限于与钢柱连接处的局部变形,因而对计算结果影响非常小,尤其对结构的整体响应特征几乎没有影响;另一方面,因平台主体过于巨大,如均采用弹塑性模型进行分析,计算量过大,很难完成有效分析,因而目前常见的水动力分析软件在计算过程中均须把平台主体视作刚体进行分析。因此,本文在计算过程中亦将平台主体假定为刚体,将荷载施加点的位移时程施加到平台模型上,在ANSYS中进行动力时程分析。
1.4.1 加速度响应
3个不同高度的结构各楼层质点加速度峰值如图6所示。由图6可知:结构加速度峰值随高度的增加近似呈线性增长;S3各楼层的加速度峰值略小于S6和S9各楼层,而S6各楼层的加速度峰值则与S9各楼层基本相当。
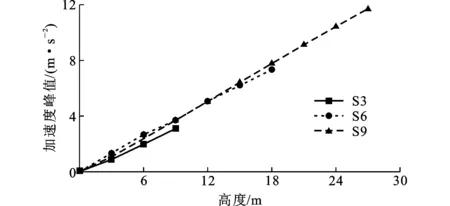
图6极端海况上承结构加速度峰值Fig.6Peak Acceleration of Top Structure Under Extreme Sea State Condition
1.4.2 位移响应

图7极端海况上承结构最大位移响应Fig.7Maximum Displacement Response of Top Structure Under Extreme Sea State Condition
极端海况下,上承结构各楼层的最大层间位移角以及各楼盖的最大相对侧移如图7所示。其中楼盖的最大相对侧移是指,以迎浪方向一个角柱的柱底作为参考点,该角柱与每层梁板的交点作为考察点,考察点与参考点在横向的最大相对位移。显然,考虑到极端海况下平台会产生大幅度的摇动,这里定义的层间位移角和相对侧移不仅包含了变形引起的位移,也包含了刚体转动引起的位移。另外,这里定义的层间位移角和相对侧移都是作用时段的最大值,并不具有时间对应性,因而相对侧移与层间位移角之间并无直接关联。由图7可知:
(1)上承结构各楼层的最大层间位移角分布较为复杂。S3的最大层间位移角在第1层最大,第2层和第3层基本相当;S6的最大层间位移角从第1层至第3层逐渐增加,在第4层突然减小至最小值,然后再增加至与第1、2层大致相当的水平,总体曲线接近于S形;S9的最大层间位移角在第1层最大,然后逐渐减小,至第4层时达到最小值,之后从第4层到第6层又不断增加,最后从第6层到第9层又基本保持不变,总体曲线接近于C形。上述最大层间位移角的复杂分布主要是由于海浪、海流、海风共同组合而成的海洋环境作用比较复杂、组合的随机性较大等因素造成的。相比而言,S3与S6最大层间位移角的水平总体相差不大,而S9的最大层间位移角则明显大于S3与S6的。
(2)上承结构各层楼盖最大相对侧移分布相对简单,3个结构都随高度的增加而近似呈线性增大。相比而言,S3与S6前三层的楼盖最大相对侧移较为接近,而S9的楼盖最大相对侧移则明显大于S3和S6对应楼盖处的。
1.5适合高度建议
由第1.4节结构动力响应分析结果可知,在相同极端海况作用下,尽管不同高度结构对应楼层质点的最大加速度总体相差不大,但楼层最大层间位移角及楼盖最大相对侧移却存在明显差别,这种差别主要体现在9层结构与6层及3层结构上,即6层和3层结构的楼层最大层间位移角及楼盖最大相对侧移总体较为接近,但却均明显小于9层结构的。这表明,当结构高度大于6层时,就有可能带来结构动力响应的加速增大,因此,本文建议平台上承结构高度不宜超过6层,且以6层为相对适宜高度。
2海洋环境荷载与地震作用下上承结构动力响应特征对比分析
根据第1.5节的建议,现选取第1.1节所设定的6层钢框架结构作为基本结构模型,然后分别将其置于两种工况下进行动力响应分析,一种工况是将其固定于半潜式海洋平台上经受海洋环境荷载作用,另一种是将其固定在陆地地面上经受地震作用。钢框架及海洋平台的有限元模型仍与第1.2节的相同。
2.1荷载选取
2.1.1 海洋环境荷载
仍然采用第1.3节中的海洋基本参数设置,在此基础上,考虑海洋环境荷载水平常以有义波高来反映,这里选取有义波高差值在6 m左右的三级海洋环境荷载进行分析,这三级荷载所对应的重现期分别为1 d、4个月和100年,荷载具体参数见表5。
2.1.2 地震波的选取
基于《建筑抗震设计规范》(GB 50011—2010),根据工程场地类别为Ⅱ类、设计地震分组为第一组、抗震设防烈度为8度(0.2g,g为重力加速度)确定地震规范设计谱,进而根据规范设计谱各设计一条8度多遇及8度罕遇人工波,如图8(a)、(d)所示;同时,根据频谱特性、有效峰值和持续时间等参数相近的原则,在太平洋地震研究中心强震记录数据库中各选择两条与8度多遇及8度罕遇人工波相近的实际记录地震波(天然波),其中Friuli_Italy波和Mammoth Lakes波是与8度多遇人工波相近的天然波,Imperial Valley波和San Fernando波是与8度罕遇人工波相近的天然波,如图8(b)、(c)、(e)、(f)所示。荷载施加方向与海洋环境荷载方向相同。

表5海洋环境荷载参数Table 5Ocean Environmental Load Parameters
2.2动力时程分析
2.2.1 水平加速度响应
上承结构在3个级别的海洋环境荷载、3个8度多遇地震以及3个8度罕遇地震作用下,每个楼层质点的水平加速度峰值如图9所示。
由图9可知:
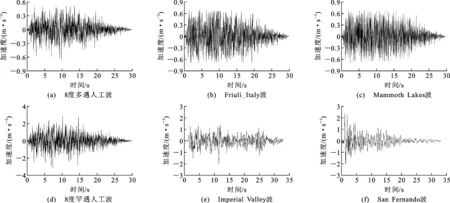
图8地震波加速度时程曲线Fig.8Time-history Curves of Seismic Acceleration

图9结构水平加速度峰值Fig.9Horizontal Peak Acceleration of Structure
(1)3个级别海洋环境荷载作用下上承结构的加速度峰值随高度的增加近似呈线性增长,且随荷载级别的增加,结构加速度峰值也在增大;3个8度罕遇地震作用下上承结构的加速度峰值随高度的增加总体上也接近线性增长,只是第5、6两层稍有偏离;3个8度多遇地震作用下上承结构的加速度峰值随高度的增加呈非线性变化趋势,尤其在第4、5层还出现了下降,到第6层又增长。
(2)海洋环境荷载作用下上承结构的加速度峰值全面小于8度罕遇地震作用下上承结构的加速度峰值,其中最大的100年一遇海洋环境荷载引起的加速度峰值不及最大的8度罕遇人工地震波引起的加速度峰值的一半;另一方面,海洋环境荷载引起的加速度峰值总体上也小于8度多遇地震引起的加速度峰值,但其中最大的100年一遇海洋环境荷载引起的加速度峰值在第4、5、6三层部分超过8度多遇地震引起的加速度峰值。
2.2.2 角加速度响应
与地震作用相比,海洋环境荷载作用下结构呈更为显著的六自由度运动,且平面外的运动对结构的影响较大,故这里对结构平面外运动进行探究,提取上承结构绕图3所示A轴转动的角加速度,如图10所示。
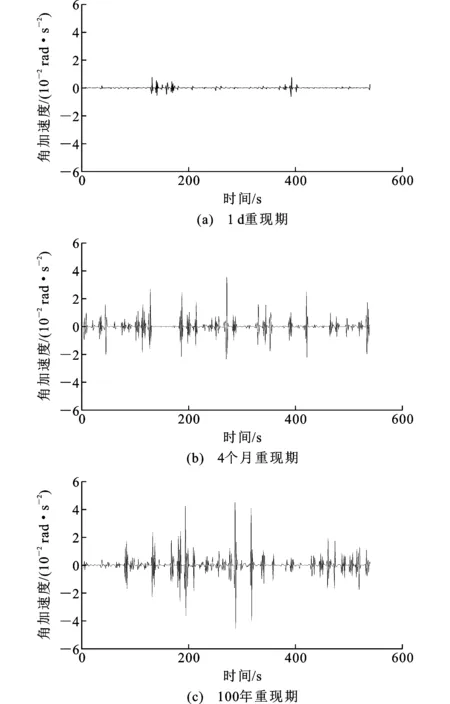
图10海洋环境荷载下平台上承结构角加速度时程曲线Fig.10Time-history Curves of Angular Acceleration of Top Structure Under Ocean Environmental Load
由图10可知:随荷载级别的增加,角加速度的峰值也在增大,但从1 d到4个月重现期的增大非常显著,而从4个月到100年重现期的增大则相对较小。原因在于:当海洋环境荷载较小时,结构摇动平衡主要依赖结构-水系统自身的回复力,此时荷载的增加会引起摇动响应的显著增大;然而,当海洋环境荷载较大以后,结构摇动平衡转为主要依赖系泊系统提供的回复力,鉴于系泊系统可提供较大刚度的约束,此时荷载的增加就不再会引起摇动响应的显著增大。
2.2.3 位移响应
图11、12分别为3个级别海洋环境荷载与3个8度多遇地震、3个8度罕遇地震作用下,每个楼层的最大层间位移角及每层楼盖的最大相对侧移。由图11、12可知:
(1)关于上承结构各楼层最大层间位移角的分布,在海洋环境荷载作用下,除了100年一遇极端海况下呈较复杂的S形之外,1 d和4个月一遇海况下均呈近似的铅垂直线形分布;在8 度多遇地震作用下,最大层间位移角的最小值均出现在第1层,最大值出现在第2层(Friuli_Italy波和Mammoth Lakes波)或第3层(人工波),第2层(或第3层)往上逐渐小幅减小;在8度罕遇地震作用下,最大值均出现在第2层,第2层往上逐渐以较大幅度减小。
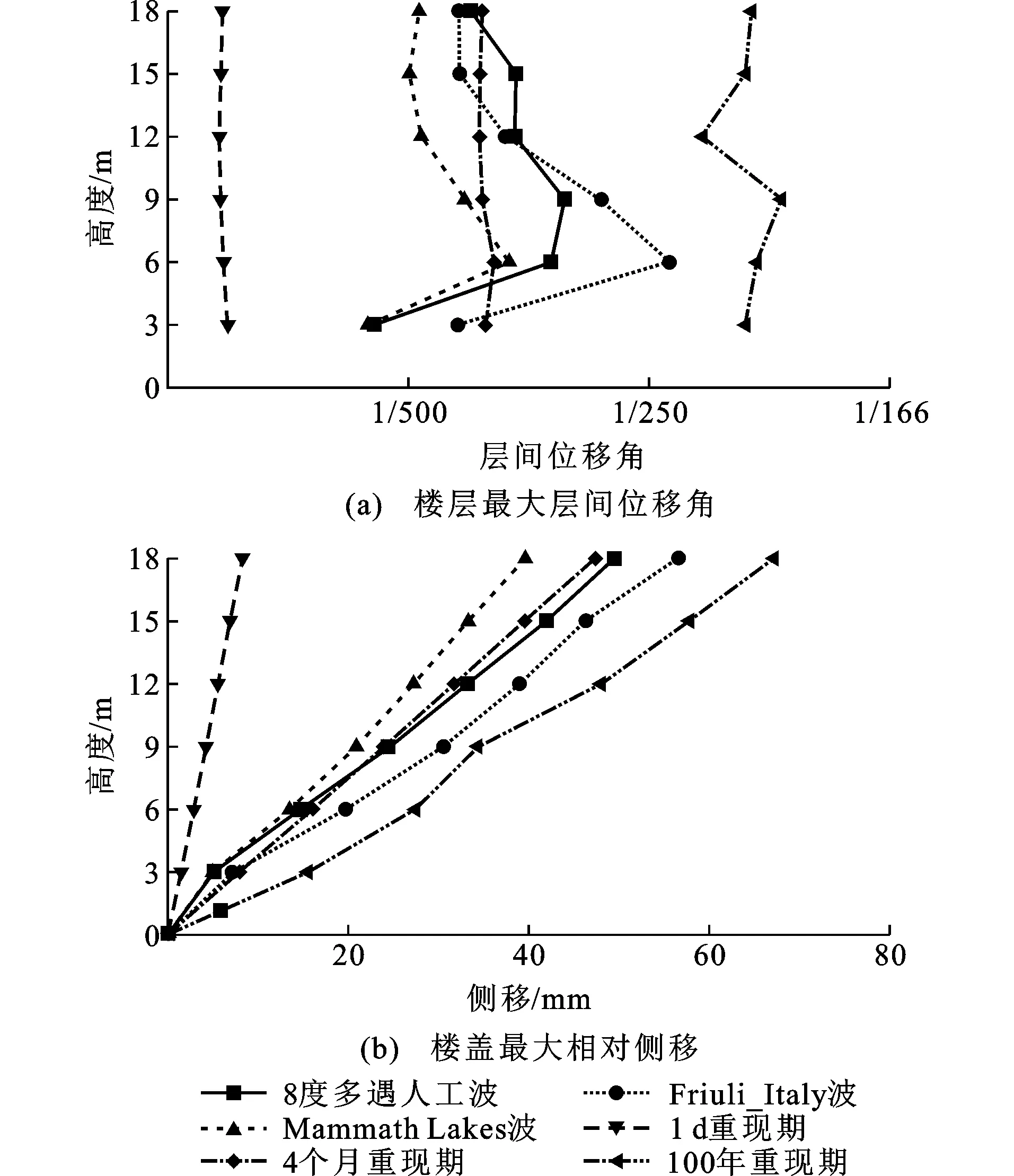
图118度多遇地震及海洋环境荷载下结构位移响应Fig.11Displacement Response of Structure Under 8 Degree Frequent Earthquake and Ocean Environmental Load
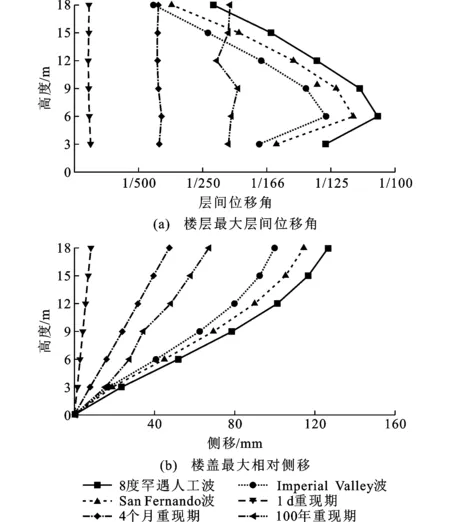
图128度罕遇地震及海洋环境荷载下结构位移响应Fig.12Displacement Response of Structure Under 8 Degree Rare Earthquake and Marine Environmental Load
(2)关于上承结构各楼层最大层间位移角的大小关系,4个月一遇海况下与8度多遇地震下各楼层的最大层间位移角大小总体基本相当,而1 d和100年一遇海况下各楼层的最大层间位移角总体上分别小于和大于8度多遇地震下各楼层的最大层间位移角;另一方面,3种海况下各楼层的最大层间位移角总体上明显小于8度罕遇地震下各楼层的最大层间位移角,只有100年一遇海况下第6层的最大层间位移角全面大于3个8度罕遇地震下第6层的最大层间位移角。
(3)关于上承结构各层楼盖最大相对侧移的分布,3种海况下及8度多遇地震下都随高度的增加近似呈线性增大,而8度罕遇地震下则呈非线性增大,即从第1层到第2层增大较快,从第2层往上增大越来越慢。
(4)关于上承结构各层楼盖最大相对侧移的大小关系,4个月一遇海况下与8度多遇地震下各层楼盖最大相对侧移大小总体基本相当,1 d一遇海况下各层楼盖最大相对侧移全面显著小于8度多遇地震下各层楼盖最大相对侧移,100年一遇海况下各层楼盖最大相对侧移全面略大于8度多遇地震下各层楼盖最大相对侧移;另一方面,3种海况下各层楼盖最大相对侧移总体上明显小于8度罕遇地震下各层楼盖最大相对侧移。
3结语
(1)在100年一遇海洋环境荷载作用下,6层(高18 m)与6层以下高度的上承结构各层的动力响应水平都相对较小且相互之间的差距也不大;高于6层以后,结构的动力响应水平因海风及结构倾斜影响过大而比6层结构的有显著增大。因此,海洋平台上承房屋钢框架结构的高度不宜超过6层(高18 m)。
(2)6层房屋钢框架结构的最大层间位移角当在陆地上经受8度抗震设防烈度多遇与罕遇地震作用时,自下而上呈先增加后减小的发展趋势,最大值基本都出现在第2层;当在平台上经受1 d、4个月和100年一遇海洋环境荷载作用时,自下而上总体上基本相等,近似呈铅垂直线形分布,只是100年一遇作用时略有偏离,接近较弱的S形。
(3)6层房屋钢框架结构的最大相对侧移当在平台上经受1 d、4个月和100年一遇海洋环境荷载作用时以及在陆地上经受8度抗震设防烈度多遇地震作用时,都随高度的增加近似呈线性增大,但在陆地上经受8度抗震设防烈度罕遇地震作用时,则随高度的增加而呈非线性增大,即从第1层到第2层增大较快,从第2层往上增大越来越慢。
(4)平台支承海洋环境作用与陆地支承地震作用两种条件下6层房屋钢框架结构的动力响应在4个月一遇海况下与8度多遇地震下的响应水平总体基本相当,而1 d、4个月及100年一遇海况下的响应水平总体上明显小于8度罕遇地震下的响应水平。
(5)由于海洋平台结构尺度非常大,真正有效的试验验证很难实现,因此,本文只做了数值模拟研究,其结果仅具参考价值。

