曲线双工字钢组合梁桥横梁受力分析研究
闫新凯,刘永健,2,邢子寒,封博文,陈 霄
(1. 长安大学公路学院,陕西西安 710064; 2. 长安大学公路大型结构安全教育部工程研究中心,陕西西安 710064)
0引 言
由于钢混组合梁桥能充分利用各材料的性能,具有较高的承载能力,因此在高速公路桥梁以及市政桥梁中广泛应用。其中双工字钢组合梁桥具有施工简捷高效、工业化程度高、结构构造简单、技术经济性高等诸多优点[1-2],在国内外已经有很多实践。2020年6月19日,中国最长的钢板组合梁桥西镇高速公路西乡泾洋河特大桥完成了合龙,并且在弯道最集中的6.04 km路段创新采用了中国规模最大的双工字钢板组合梁桥结构。曲线双工字钢组合梁桥作为开口截面,其抗扭刚度较小[3],截面可能会发生较大的翘曲变形。为保证截面形状不变,横梁发挥了非常明显的作用。跨中截面上,横梁将侧向荷载传给梁;支座截面处,横梁将扭转荷载转换成支座竖向以及横向的支反力[4]。

图1曲线双工字钢板组合梁桥Fig.1Curved Steel-concrete Composite Twin I-girder Bridge
目前,部分学者对横梁受力做了一系列研究,认为横梁内力可以近似采用简化方法V-load法来确定,V-load法与M/R法[5]类似,都是曲线梁桥简化计算方法,区别在于V-load法适用于工字梁而M/R法适用于箱梁。国外学者Jr Peollet[6]记载了V-load法的发展;Liu等[7]认为在水平弯曲钢梁分析中,若允许忽略曲率作用,横梁力可以根据V-load法进行确定。此外,作者给出了适用于2主梁到8主梁结构的横梁端部弯矩以及剪力的计算表格,并以一个5主梁结构设计实例进行了横梁内力计算。对于如图1所示双工字钢板组合梁,学者们一般将钢主梁、桥面板以及横梁组成的空间结构简化为框架模型来进行分析。Xiang等[8]在研究外荷载作用下横梁截面混凝土板的横向弯矩分布时,提出了一种横梁截面框架模型来分析横向弯矩分配系数,但该模型仅适用于竖向荷载作用于桥面板上的情况。拉伯特等[9]提出的横梁简化框架模型则考虑了侧向水平风荷载或曲率效应产生的侧向水平分力作用,但该框架模型仅考虑了框架平面内变形,并未考虑由于主梁腹板纵桥向翘曲使得横梁发生的纵桥向变形。在曲线双工字钢组合梁中,主梁腹板的纵桥向翘曲变形尤其突出。
为此,本文采用符拉索夫薄壁结构理论分析了曲线双工字钢组合梁桥的翘曲变形以及结构扭转角等物理现象,研究了横梁纵桥向变形对现有横梁框架模型应力分布的影响,最终通过有限元分析验证了其截面正应力分布规律,并给出了相应的设计建议。
1横梁受力与变形
图2为横梁内力示意图,将图2(a)所示横梁看成支撑在主梁腹板之间的杆件,其中Mx和Mz分别为绕工字型横梁截面强轴和弱轴的弯矩,F为横梁截面轴向受力。规定Mx为横梁截面竖向弯矩,Mz为横梁截面纵桥向弯矩[10]。

图2横梁内力Fig.2Internal Force of Crossbeam
当横梁框架作用侧向水平荷载时,横梁会受到竖向弯矩Mx和轴向力F作用,并且Mx和F可根据现有框架模型[9]计算得出。由于横梁与主梁腹板的变形协调作用,当考虑主梁的纵桥向翘曲变形时,框架模型中横梁便会产生纵桥向的变形,横梁截面会受到纵桥向弯矩Mz作用。
1.1现有框架模型
拉伯特等[9]提出不同位置的横梁框架模型,跨内横梁简化为如图3所示横梁框架模型进行简化计算。

图3横梁框架模型Fig.3Crossbeam Frame Model
传递侧向水平荷载是横梁的基本功能,图3所示横梁框架模型可能受到的侧向荷载主要包括:
(1)风荷载。跨内的横梁将风荷载传递给桥面板,支点处横梁则是把从跨内桥面板传来的风荷载全部传递给支座。
(2)曲线桥曲率作用。曲率作用下,主梁截面轴向力会产生径向分力作用,桥面板以及钢梁上翼缘的径向分力直接作用在桥面板,钢主梁下翼缘径向分力则直接作用在横梁框架模型上,最终传递至桥面板。
(3)侧向扭转屈曲的约束力。为保证支点受压翼缘不会发生侧向扭转屈曲,横梁会产生水平方向力,该作用力也可认为作用在框架模型上的侧向力。
对于曲线双工字钢组合梁桥,当结构只承受跨中竖向集中荷载且不承受风荷载时,跨内横梁框架模型侧向荷载主要来源于曲率作用下主梁截面正应力的径向分力。对于曲线双工字钢组合梁,截面正应力由弯曲正应力与翘曲正应力组成,为了简要说明问题,将曲线双工字钢梁桥截面应力简化为如图4(a)所示,并等效为图4(b)所示的一组“截面假想力”P。由于曲率作用[图4(c),其中R为曲率半径],这组“截面假想力”会产生沿曲线径向分力,在跨内上翼缘的径向分力通过桥面板传递到支点截面,下翼缘径向分力则作用于图4(d)所示横向框架模型。在曲线中,2片主梁下翼缘正应力大小不相等,导致等效径向分力P1与P2不相等,依据结构力学[11]框架计算,横梁会产生框架面内竖向弯曲变形和轴向变形,因此横梁内梁侧与外梁侧的应力分布如图5(a)、(b)所示,将对横梁产生的这种力学效应定义为“竖向弯曲效应”。
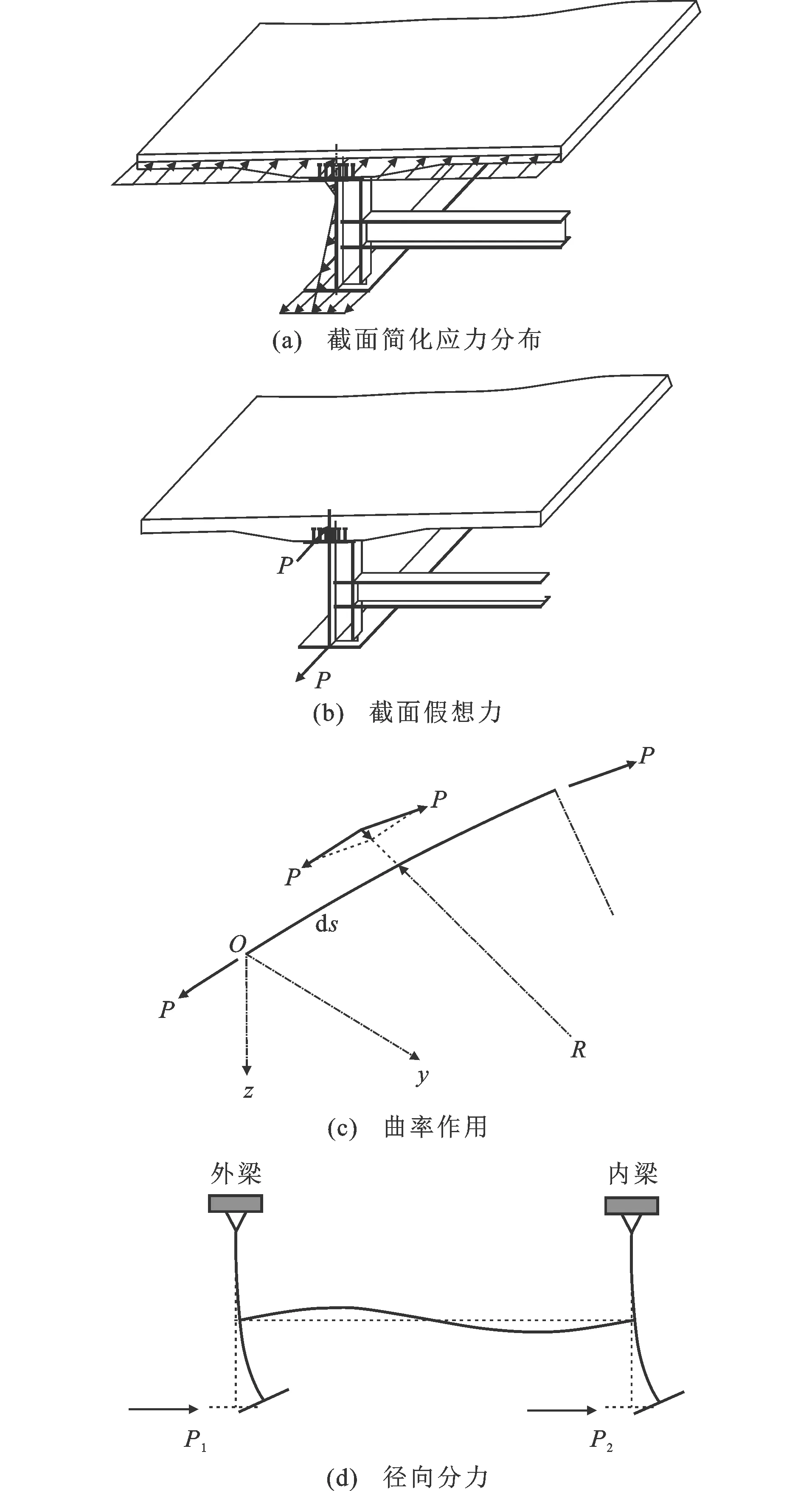
图4曲线梁曲率作用Fig.4Curvature Action of Curved Beam
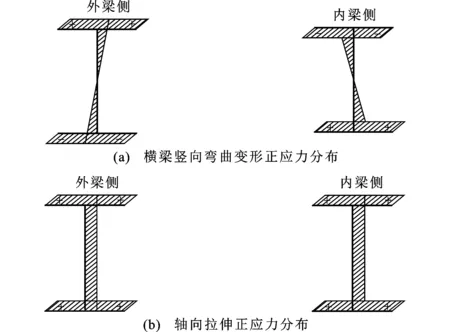
图5横梁框架模型正应力分布Fig.5Positive Stress Distribution of Crossbeam Frame Model
1.2横梁纵桥向变形
如前所述,横梁的纵桥向变形是由于主梁腹板的纵桥向翘曲变形不一致导致。主梁翘曲产生的原因是曲线双工字钢组合梁为开口截面,需要依靠主梁的纵桥向变形来平衡扭矩[12],因此需要先进行曲线双工字钢组合梁的约束扭转分析。
双工字钢组合梁桥由于截面厚度相对于其长度或宽度来讲较小,因此双工字钢组合梁桥在一定的尺寸范围内可被视为薄壁杆件[13],其长度、宽度(高度)和厚度应满足

(1)
(2)
式中:d为截面轮廓曲线上的壁厚;Ec和Es分别为混凝土和钢的弹性模量;dc和de分别为混凝土桥面板厚度和混凝土桥面板等效为钢板的等效厚度;b为截面的最大高度或宽度,对于双工字钢组合梁而言,最大宽度为支点截面支座间距;l为杆件长度。
对开口截面发生的约束扭转做如下2个基本假定:
(1)在小变形情况下,截面轮廓在自身平面内不发生变形。
(2)杆件中面上剪应变为0。
截面上任一点的翘曲位移u(x,s)可定义为
u(x,s)=-φ′(x)w(s)+u0(x)
(3)
式中:φ′为扭率;w为截面主扇性坐标;s为截面曲线坐标;u0(x)为截面x轴上s=0处的纵向翘曲位移。
曲线梁扭转角如图6所示,它主要包括两部分:一是与直梁相同的绕截面x轴的扭转角τ,二是弯桥特有的截面挠度h产生的扭转角h/R。由此可得曲线梁总扭转角φ为
(4)

图6曲线梁扭转角Fig.6Torsion Angle of Curved Beam
考虑曲线梁沿梁长方向外荷载轴力为0,依据符拉索夫理论[13-15],曲线开口截面约束扭转微分方程为
(5)

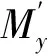
(6)
式中:Qy为竖向剪力;T为梁承受的扭矩。
对于式(5)的微分方程,需要先求解出沿梁长的竖向弯矩分布。对于式(6)来讲,现有简支梁两端都约束了梁的扭转,因此对于扭转而言是一次超静定结构,需要根据力法求出梁的内力分布。得到内力分布后,再采用式(7)初参数方程求解式(5)的微分方程。
X(x)=D(x)X0
(7)
(8)

双工字钢组合梁任意截面的状态向量表示为
(9)
式中:B和L分别为截面的翘曲双力矩和扭矩。
假设曲线梁截面沿梁长相同,图7所示的曲线简支梁杆系模型承受偏心集中荷载时,各物理参数计算公式如式(10)、(11)所示。

图7曲线简支梁杆系模型Fig.7System Model of Simply Supported Curved Beam
当0≤θ≤β时
(10)
当β<θ≤α时
(11)

选取截面尺寸如图8所示的π形钢梁做算例分析,简支曲线梁梁长18 m,曲线半径20 m,截面尺寸满足式(1)薄壁杆件尺寸要求,因此可用公式(10)、(11)进行计算。在跨中lp=9 m处的腹板正上方施加竖向偏心荷载P=400 kN,偏心距e=1 675 mm。材料弹性模量为2.06×105MPa,泊松比为0.3。

图8截面尺寸(单位:mm)Fig.8Section Size (Unit:mm)
根据式(10)、(11)可得偏心集中荷载作用下简支曲线梁各物理参数沿梁长的分布规律,具体如图9所示。由图9可知,翘曲双力矩分布与弯矩分布规律类似,曲率作用产生的扭矩不可忽略且与外扭矩一起从加载点截面向两端支座传递,扭转角在加载点截面处最大,扭率在加载点两侧呈现正负相反的趋势。
π形梁截面的主扇性坐标w如图10所示,点A代表主扇性零点。由式(3)可知,同一截面左右两腹板同一高度处的翘曲位移不一致,由于腹板与横梁的变形协调作用,横梁左右两端沿着纵桥向的变形也不一致,导致横梁发生纵桥向的弯曲。加载点两 侧扭率相反,因此加载点两侧的主梁翘曲变形方向相反,变形协调作用进而导致横梁的纵桥向变形方向相反。此外,当横梁越靠近下翼缘时,两侧主梁腹板翘曲变形差越大,导致横梁纵桥向弯曲变形更明显。
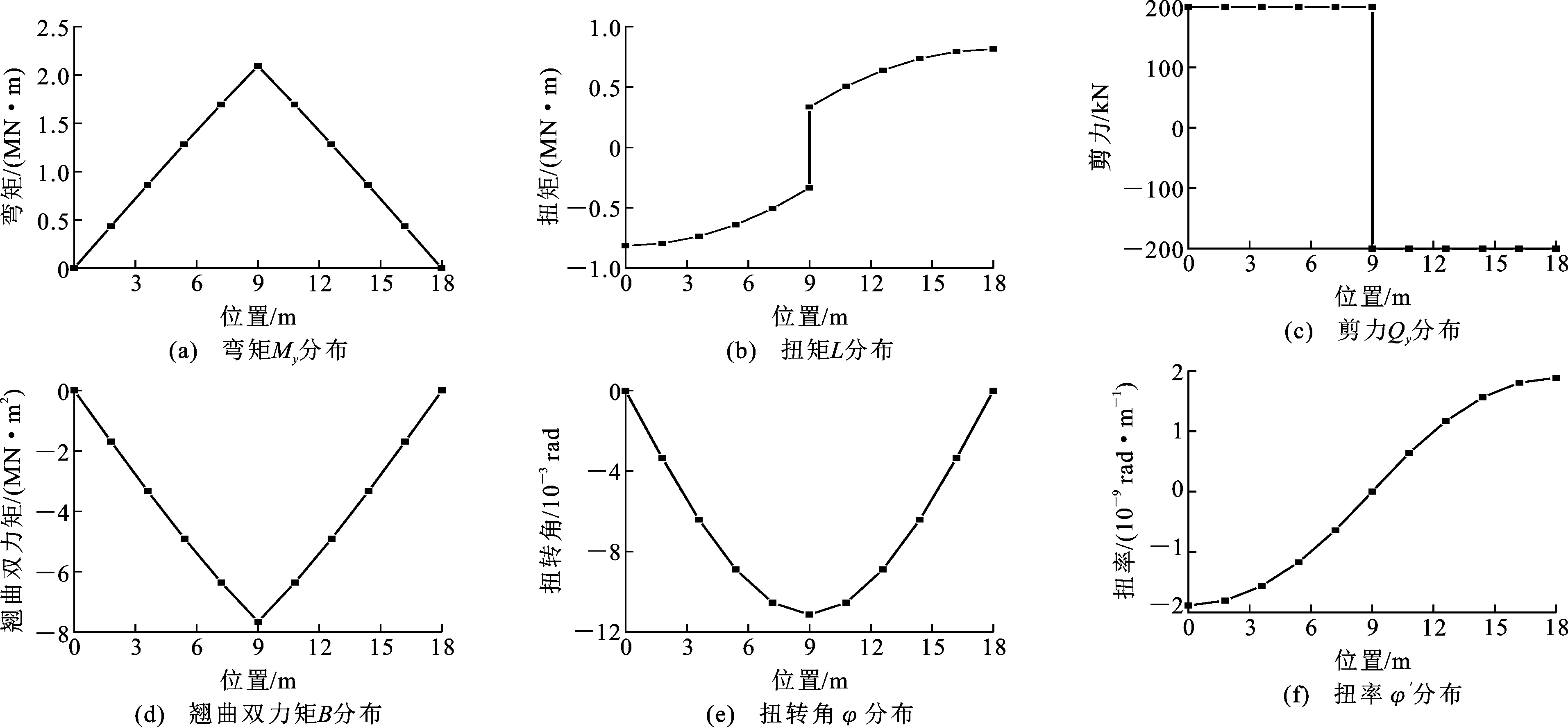
图9各物理参数计算结果Fig.9Calculation Results of Each Physical Parameter

图10主扇性坐标Fig.10Principal Sectoral Coordinate
与算例中的π形钢梁不同,实际结构中双工字钢组合梁桥的约束扭转分析需要考虑横梁对结构整体抗扭刚度的影响。Zhang等[18]提出可采用将横梁刚度连续化的方法处理横梁对这种开口截面约束扭转计算的影响,反映在约束扭转微分方程中为
(12)
式中:Kd为横梁刚度连续化处理后的等效刚度。
由式(12)可以看出,考虑了横梁的开口截面约束扭转微分方程的形式与不考虑横梁的完全一样,只是其圣维南扭转刚度增大了,并且由于横梁数量少,Kd相对于K很小[19],计算得到的规律也基本一致。因此可以采用算例中π形钢梁的约束扭转规律来类比说明带有横梁的组合梁的约束扭转规律。
曲线双工字钢组合梁在偏载作用下截面的效应由竖向弯曲作用和约束扭转作用组成。在竖向弯曲作用下,内外侧主梁沿着纵桥向产生相同的纵向变形Lh;在约束扭转作用下,截面会产生翘曲变形,由图10以及式(3)可知,同一截面处,内外侧主梁腹板会产生相反的翘曲变形Lw。式(13)即为2种效应变形叠加后的结果,总体变形如图11所示。腹板的纵桥向变形L1与L2不一致,会导致横梁发生纵桥向反对称变形。纵桥向的弯曲变形使得横梁内梁侧与外梁侧的应力分布如图12所示,将这种力学效应定义为“腹板变形不一致效应”。
(13)
式中:L1与L2分别为内外梁腹板沿纵桥向的总变形。
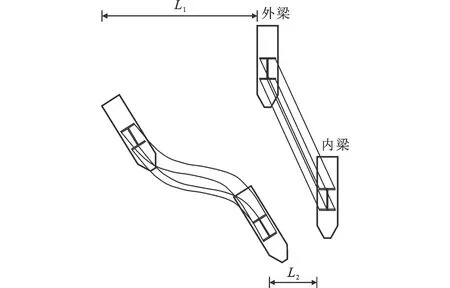
图11横梁纵桥向变形分析Fig.11Analysis of Longitudinal Bridge Deformation of Crossbeam

图12横梁纵桥向弯曲应力Fig.12Longitudinal Bridge Bending Stress of Crossbeam
1.3应力叠加
将上述“竖向弯曲效应”与“腹板变形不一致效应”相叠加,可得横梁的截面总正应力分布,如图13所示。由图9计算结果可得:靠近加载点截面弯矩与翘曲双力矩较大而扭率较小,因此横梁以“竖向弯曲效应”为主导;靠近支点截面弯矩与翘曲双力矩较小而扭率较大,横梁以“腹板变形不一致效应”为主导。

图13横梁截面总正应力分布Fig.13Sectional Total Positive Stress Distribution of Crossbeam
2基于有限元分析的横梁截面应力分布规律
2.1有限元模型
为验证上述正应力分布规律,拟定的简支曲线双工字钢组合梁桥总体布置如图14所示,截面布置如图15所示,计算跨径L′=18 m,曲率半径R=100 m,各部件尺寸见表1。为进一步探究横梁在腹板高度位置不同的影响,拟定2种模拟工况:工况一,横梁在腹板中心高度,即横梁中心距离下翼缘410 mm;工况二,横梁中心距离下翼缘180 mm。钢梁选用Q345钢材,弹性模量为2.06×105MPa,泊松比为0.3;混凝土桥面板采用C50混凝土,弹性模量为3.45×104MPa,泊松比为0.2。经计算,该截面尺寸满足薄壁杆件要求,可以采用符拉索夫理论对其进行分析。在跨中内梁腹板正上方施加竖向偏心荷载P=1 000 kN,偏心距e=1 675 mm,建立如图16所示的有限元模型。其中桥面板采用C3D8R实体单元模拟,钢主梁以及横梁采用S4R板壳单元模拟[20],桥面板与钢主梁之间采用绑定(Tie)接触,忽略桥面板与钢主梁之间的滑移。
2.2横梁结果提取点编号规则
横梁编号如图17(a)所示,编号顺序从左到右依次为1#~4#横梁。在每根横梁上提取2个截面正应力,分别距离内侧钢梁及外侧钢梁T形加劲肋30 cm,如图17(b)所示。每个断面提取4个节点正应力,位置及编号如图17(c)、(d)所示。

图14曲线双工字钢组合梁桥总体布置(单位:mm)Fig.14General Layout of Curved Steel-concrete Composite Twin I-girder Bridge (Unit:mm)

图15标准横截面(单位:mm)Fig.15Standard Cross Section (Unit:mm)
2.3工况一横梁截面正应力沿梁长分布规律
1#横梁内梁侧与外梁侧荷载-应力曲线如图18所示。由图18可知,NU1、NU2受压,NB1、NB2受拉,WU1、WU2受拉,WB1、WB2受压,说明“竖向弯曲效应”使1#横梁在竖向发生了反对称的弯曲变形,内梁侧为正弯矩,外梁侧为负弯矩。由图18亦可知:同一翼缘处,NU2应力大于NU1,NB1应力大于NB2;WU2应力大于WU1,WB1应力大于WB2,说明横梁翼缘左右两侧应力不一致,横梁发生纵桥向弯曲变形。U2、B1对角线应力大于U1、B2对角线应力,说明其为“竖向弯曲效应”与“腹板变形不一致效应”叠加而得。
2#~4#横梁各自内外梁侧应力变化规律与1#横梁类似,为探究应力分布沿梁长的变化规律,绘制1#~4#横梁内梁侧荷载-应力曲线结果,如图19所示。相较于1#横梁,2#横梁NU2应力较大,原因为2#横梁截面靠近加载点,下翼缘拉应力水平大于1#横梁截面,由于曲率产生的径向分力增加,进而导致横梁框架效应增加。2#横梁NU1与NU2、NB1与NB2应力差值明显小于1#横梁,其原因是2#横梁距离加载截面比较近,由图9(f)可知,2#横梁截面扭率小于1#横梁截面,进而导致内、外梁腹板变形差减小,使2#横梁纵桥向弯曲小于1#横梁。

表1各部件尺寸Table 1Dimensions of Each Component
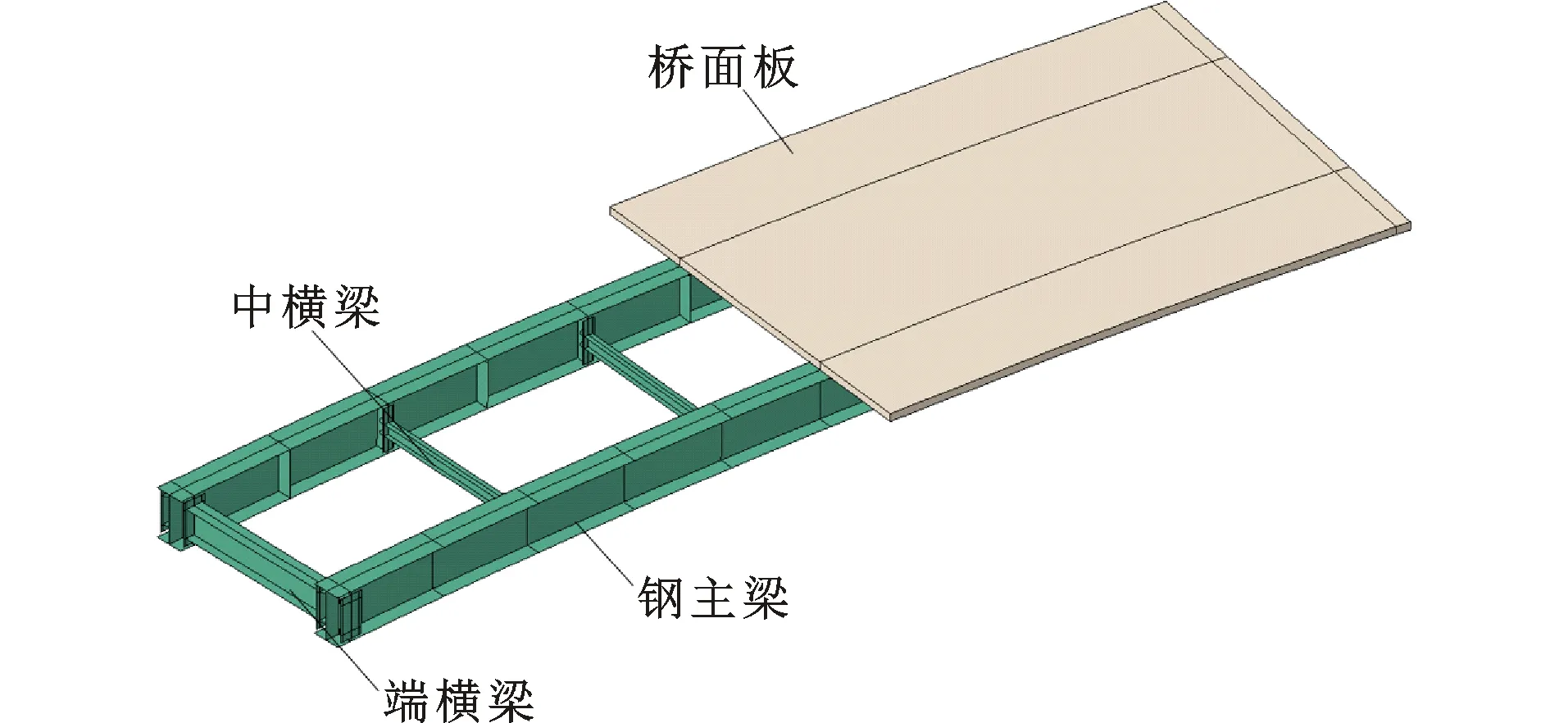
图16有限元模型Fig.16Finite Element Model

图17提取点位置及编号顺序Fig.17Location and Numbering Sequence of Extraction Points

图181#横梁应力分布Fig.18Stress Distribution of 1# Crossbeam

图191#~4#横梁内梁侧应力分布Fig.19Stress Distribution on Inner Beam Side of 1#-4# Crossbeam
由图19(c)、(d)可知,3#与2#横梁、4#与1#横梁的应力大小基本一致,不同点在于,1#与2#横梁U2、B1对角线应力大于U1、B2对角线应力,3#与4#横梁U1、B2对角线应力大于U2、B1对角线应力,原因是3#与4#横梁在加载点另一侧,而加载点截面两侧由于扭率正负相反使得翘曲变形方向相反,从而导致3#与4#横梁纵桥向弯曲方向与1#、2#横梁相反。
2.4工况一、二横梁正应力沿腹板高度分布规律对比
为了进一步探究横梁应力沿腹板高度的分布规律,将2种工况1#横梁内梁侧荷载-应力曲线进行对比,结果如图20所示,工况二中U1与U2(B1与B2)应力差值均大于工况一。原因在于工况二横梁位置低于工况一,正如前文提到,当横梁越靠近下翼缘时,两侧主梁腹板翘曲变形差越大,进而导致横梁纵桥向弯曲作用更明显。
2.5截面应力解析
工况一中1#~4#横梁在偏心荷载P=1 000 kN作用下内外梁侧的应力值见表 2。对横梁应力值进行解析,可得拉伸变形产生的正应力σ1、竖向弯曲变形产生的正应力σ2以及纵桥向弯曲变形产生的正应力σ3,如式(14)~(17)所示,U1、U2的计算方法同B1、B2。应力解析结果见表3。由表3可知,拉伸变形与竖向弯曲变形产生的应力值之比为0.27,说明曲线桥中横梁框架存在明显的轴向力。纵桥向弯曲变形与竖向弯曲变形产生的应力值之比最大值为0.37,说明翘曲变形导致的横梁框架的纵桥向变形作用不应被忽略,该作用会使得横梁截面应力显著变化;该比值在1#与4#横梁处大于2#和3#横梁处,说明越靠近支座截面,曲线梁翘曲变形越大,横梁纵桥向弯曲变形越明显。
横梁竖向和纵桥向弯曲应力如图21、22所示。由于横梁数量较少,将各效应解析值进行拟合,可以发现竖向弯曲变形产生的应力值与主梁弯矩分布规律类似,纵桥向弯曲变形产生的应力与扭率分布规律类似。
(14)
(15)
(16)
(17)
式中:σU1、σU2、σB2、σB1为图17中横梁提取点处的有限元正应力计算结果;σB1′、σB2′为从总应力中解析出σ1后的中间量。
3设计建议
从上文的分析可以发现,开口截面抗扭刚度较小,主要依靠翘曲变形来抗扭。越靠近支座截面,横梁的纵桥向变形越明显。端横梁不仅能起到横向传力的作用,也能达到纵向约束的目的。由于限制了变形,支座截面附近的横梁应力会一定程度的增大,对于焊接式横梁,可能会出现引发焊缝疲劳等诸多问题。针对这些问题,提出以下两点设计建议来增强结构整体抗扭刚度:
(1)当横梁越靠近支点截面时,横梁面外变形越明显,可适当增加支点截面附近横梁弱轴抗弯强度,以抵抗面外变形。增强横梁弱轴抗弯强度的方法有改变横梁截面形式或者增加工字型横梁尺寸等。

图202种工况下1#横梁内梁侧应力分布Fig.20Stress Distribution on Inner Beam Side of 1# Crossbeam Under Two Working Conditions
(2)在曲线桥中,可以适当增加下平联,使得截面变成“拟封闭”截面,以达到提高抗扭刚度、减小翘曲变形的目的。
4结语
(1)符拉索夫薄壁结构理论适用于双工字钢组合梁桥的约束扭转分析,并且基于该理论得到的横梁应力分布规律与有限元模拟的规律基本一致。
(2)曲线双工字钢板组合梁桥跨内横梁可通过横向框架模型分析其受力模式。越靠近加载点截 面,主梁竖向弯矩越大,导致横梁的框架效应越明显。在跨内表现为2#、3#横梁效应较大,1#、4#横梁效应较小。

表2横梁应力值Table 2Stress Value of Crossbeams

表3应力解析结果Table 3Stress Analysis Results
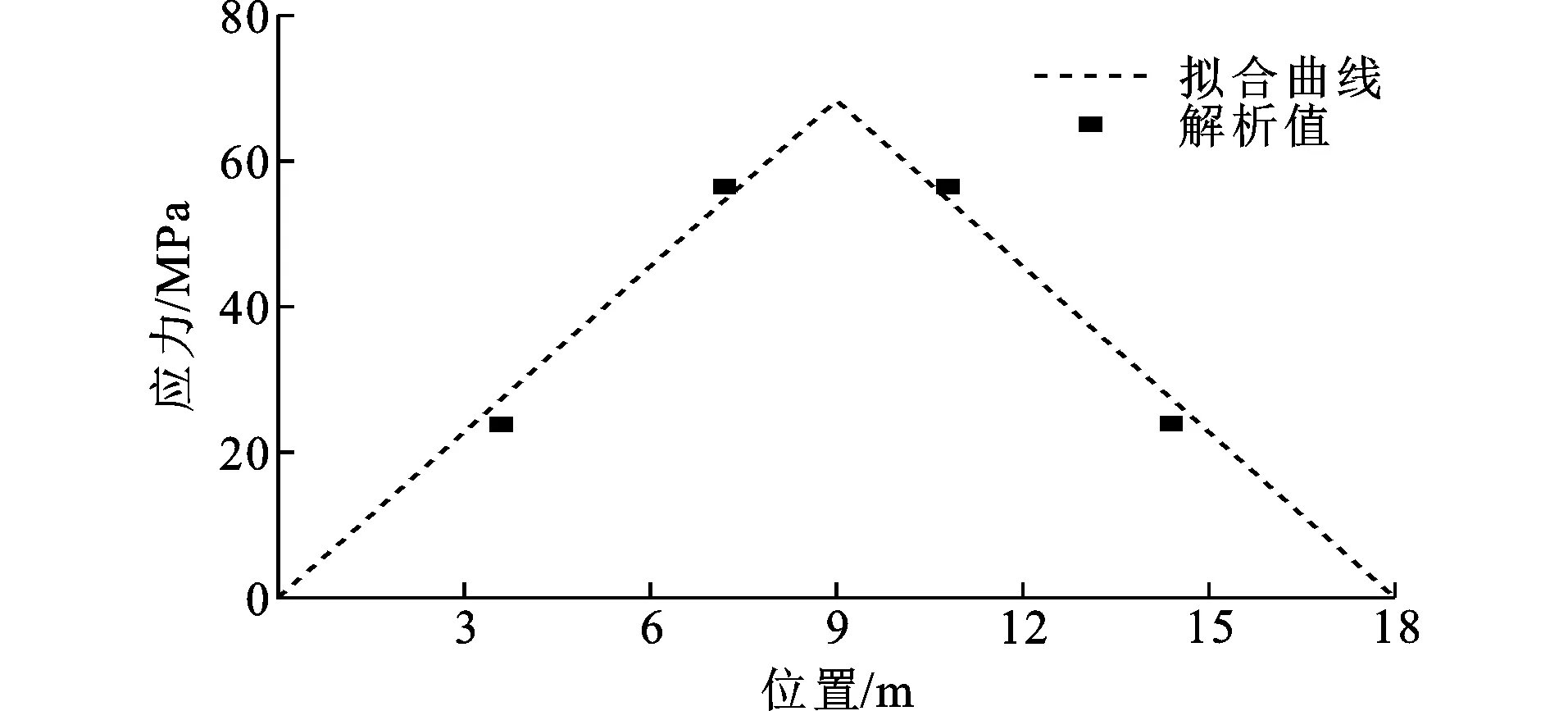
图21横梁竖向弯曲应力解析Fig.21Analysis of Vertical Bending Stress of Crossbeam

图22横梁纵桥向弯曲应力解析Fig.22Analysis of Longitudinal Bending Stress of Crossbeam
(3)约束扭转产生的翘曲变形与扭率以及截面主扇性坐标成正比,导致横梁的纵桥向弯曲变形在1#、4#横梁较大,2#、3#横梁较小,并且加载点截面两侧横梁的纵桥向变形方向相反。

