基于壁板屈曲后强度的矩形钢管混凝土偏压承载力计算方法
王海涛,刘永健,2,孙立鹏
(1. 长安大学公路学院,陕西西安 710064; 2. 长安大学公路大型结构安全教育部工程研究中心,陕西西安 710064)
0引 言
矩形钢管混凝土(RCFST)与圆钢管混凝土相比,抗弯性能优异,节点连接方便,传力可靠[1],在工程中应用越来越广泛,如钢管混凝土桁梁桥的弦杆[2-3]、缆索承重桥梁的桥塔[4]、高层建筑的框架柱[5]等。为了提高矩形钢管混凝土柱的偏压承载能力,满足大跨桥梁和超高建筑对构件的要求,可以采用增大截面尺寸、改变长宽比的方法,但该方法会使腹板的宽厚比变大,使得壁板的临界屈曲应力变小,从而更容易发生局部屈曲。当钢板正则化宽厚比大于0.5(下文简称“大宽厚比”)时,钢板发生弹塑性与弹性屈曲,屈服发生在屈曲之后[6],因此大宽厚比构件的承载能力受局部屈曲的影响较大[7]。大宽厚比钢管腹板在偏压荷载下承受非均匀压力,内侧存在混凝土的单侧约束,其极限荷载求解可归类为非均匀受压单侧约束平板的屈曲后强度问题。
Timoshenko[8]对加载边简支、非加载边具有不同支承条件的偏心加载板件的屈曲性能进行了研究,得到了板件的弹性屈曲系数。Rhodes等[9]研究了施加不同偏压荷载对板件屈曲行为的影响,结果表明对于承受恒定压缩偏心和恒定荷载偏心的板,它们的屈曲行为截然不同。Usami[10-11]使用能量法和非线性有限元法研究了矩形板在偏压荷载作用下的屈曲后强度,并提出了计算钢板极限强度的有效宽度公式。Liew等[12]研究了偏心荷载下方形和矩形大宽厚比钢箱柱的极限承载力,以及简支钢板在平面内偏压荷载下板件不同的宽厚比和荷载偏心率下的局部屈曲性能。Liang等[13]采用有限元分析方法,考虑了初始几何缺陷和残余应力,研究了薄壁钢管混凝土偏压柱侧板的临界局部屈曲和屈曲后行为,给出了确定钢管混凝土单侧约束矩形钢板临界局部屈曲和极限强度的设计公式。刘永健等[14]应用不同的特征函数描述了单侧约束矩形板在非均匀压力作用下的屈曲形态,通过伽辽金法建立屈曲控制方程组,分析了非均匀荷载作用对矩形钢管混凝土构件局部弹性屈曲性能的影响。Long等[15]基于能量法推导了偏心受压矩形钢管混凝土柱中钢板的弹性局部屈曲应力公式,研究了应力梯度系数、宽厚比和截面长宽比对矩形钢管混凝土偏心受压柱中钢板的局部屈曲行为的影响。Huang等[7]对超高强钢和高强混凝土组合的方钢管混凝土构件的偏压性能进行了试验研究,并通过有限元方法研究了不同荷载条件下的钢材屈服强度、混凝土抗压强度、壁板宽厚比等对构件承载力的影响。Nguyen等[16]对使用高强度材料的薄壁方形钢管混凝土短柱进行了偏压承载力试验研究,用经验证的有限元模型,研究了核心混凝土的约束效应以及材料强度、偏心率、截面宽厚比等对钢管混凝土柱偏压性能的影响。
国内外学者对有混凝土约束的单侧约束平板的偏压性能研究较少,未形成可进行工程应用的非均匀受压单侧约束平板的弹性屈曲系数计算公式和屈曲后强度计算方法,使大宽厚比矩形钢管混凝土的偏压承载力没有准确的计算方法。本文通过有限元方法对非均匀受压单侧约束平板的屈曲性能进行了研究,给出该类板件的弹性屈曲系数计算公式,并以此为基础,结合有效宽度法,提出大宽厚比钢管混凝土考虑腹板屈曲后强度的偏压承载力计算方法。
1非均匀受压单侧约束平板的屈曲
1.1弹性屈曲力学模型
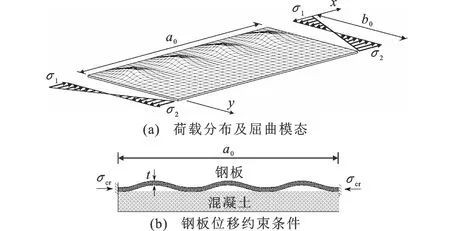
图1矩形钢管混凝土腹板非均匀受压屈曲模型Fig.1Non-uniform Compression Buckling Model of RCFST Web
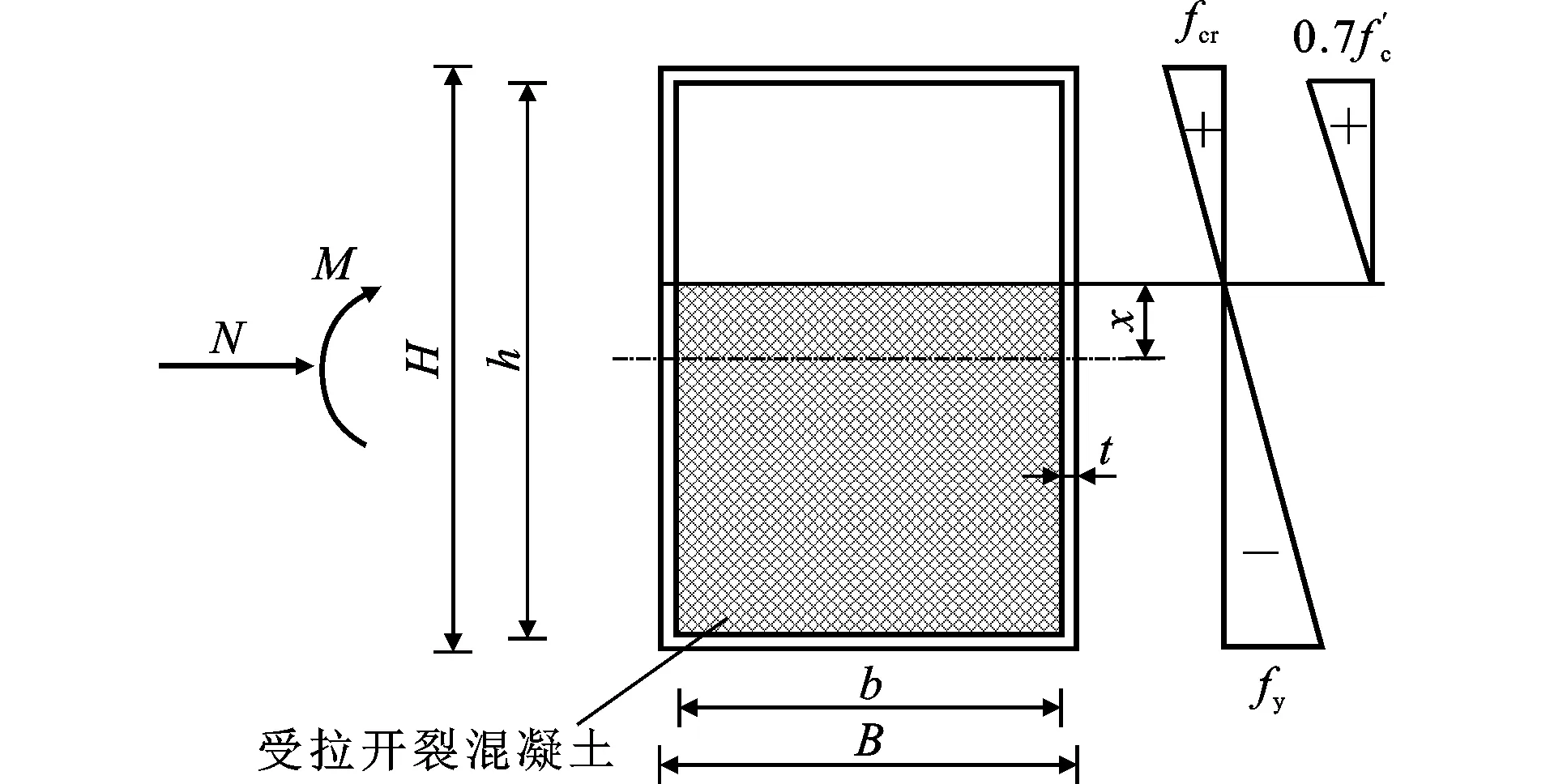
取矩形钢管混凝土偏压作用下的1块腹板为研究对象,可将其简化为1块受混凝土单侧约束的非均匀受压矩形平板,其受力与变形情况如图1所示,其中t、a0、b0分别为板件的厚度、长度、宽度,板件宽厚比为b0/t,σ1为最大应力,σ2为最小应力,σcr为临界屈曲应力。由于受到一侧混凝土的约束,板件屈曲时只能朝另一侧鼓曲且仅在受压侧存在屈曲波。不考虑钢板与混凝土界面的黏结力和摩擦作用,壁板强度降低程度在10%以内[6],为了方便对比研究计算,将其忽略。钢板加载边在压弯荷载作用下应力分布是线性的,受压为正,受拉为负。梯度荷载下的应力分布如图2所示。加载边应力梯度α=(σ1-σ2)/σ1,α=0时板件均匀受压,α=1为钢板出现拉应力的界限值,α=2时板件受纯弯作用,加载边上任意位置y处的应力σ可表达为σ=σ1(1-αy/b0)。
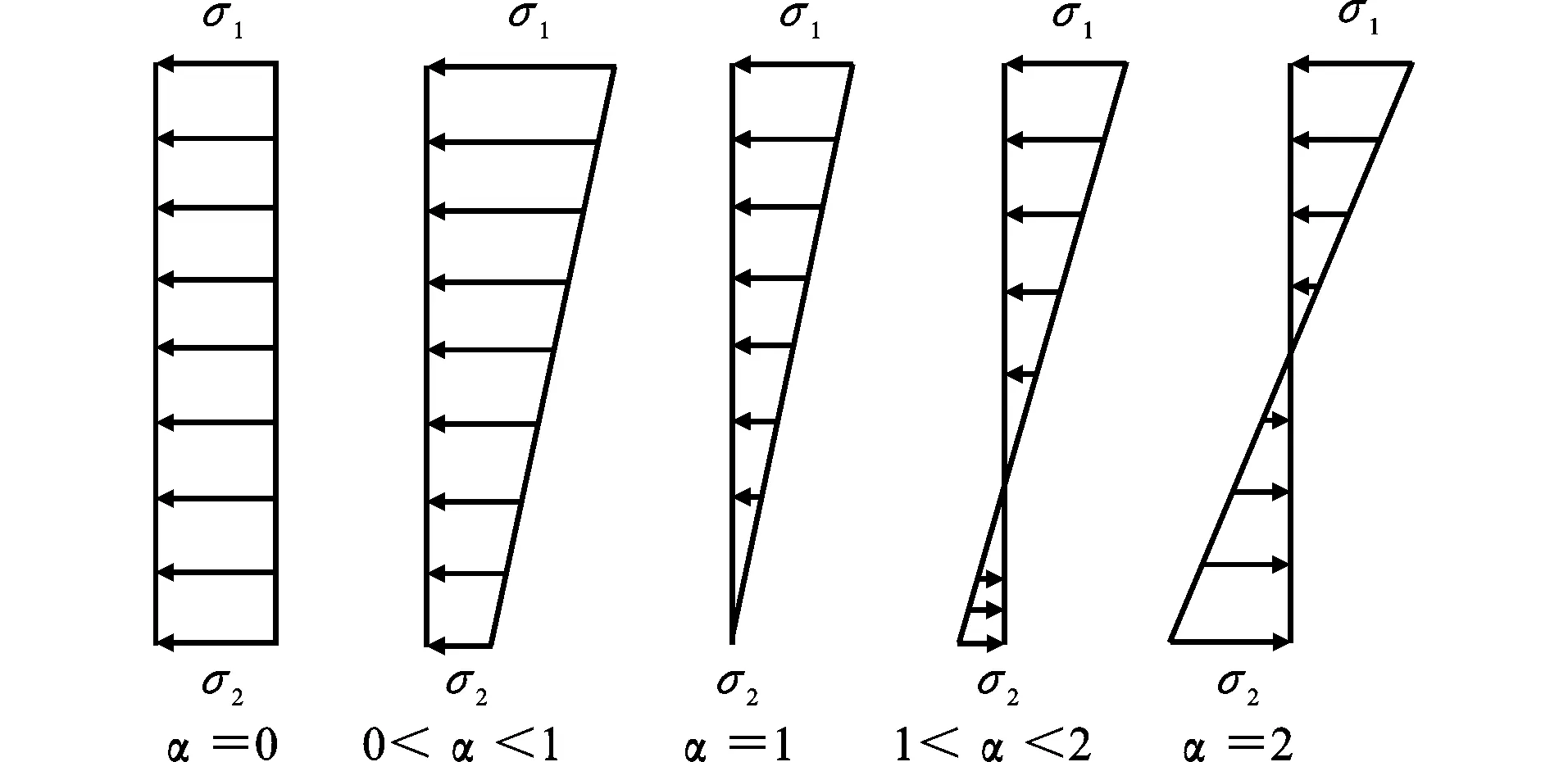
图2梯度荷载下的应力分布Fig.2Stress Distribution Under Gradient Load
σcr为板件的临界屈曲应力,即钢板发生局部屈曲时的边缘应力σ1,其表达式为
(1)
式中:k为弹性屈曲系数,k取决于板件的长宽比β与应力梯度α;E为板件的弹性模量;ν为板件的泊松比。
平板边缘的边界条件:由于混凝土的侧向约束,板件加载边绕y轴的转动约束近似为刚性约束,视为固支边界;板件的非加载边绕x轴的转动约束并非完全刚性约束,但根据孙立鹏等[6]的研究,非加载边受腹板翼缘板交汇处混凝土棱角的约束,自由转动困难,也可近似为固支边界。
1.2弹性屈曲系数
采用ABAQUS模拟非均匀受压单侧约束平板的受力过程,研究不同长宽比和不同应力梯度荷载对板件局部屈曲性能的影响,进而得到板件的弹性屈曲系数。
1.2.1 有限元分析
单侧约束钢板在非均匀受压作用下的有限元模型如图3所示,其中b′为混凝土板宽,Dx、Dy、Dz分别为x、y、z方向的自由度,Rx、Ry分别为x、y方向的转动自由度。有限元模型中钢板与混凝土均为弹性材料。钢板使用S4R减缩积分单元模拟,弹性模量Es=206 GPa,泊松比ν=0.3。混凝土使用C3D8R减缩积分实体单元模拟,弹性模量Ec=34.5 GPa,泊松比ν=0.2。
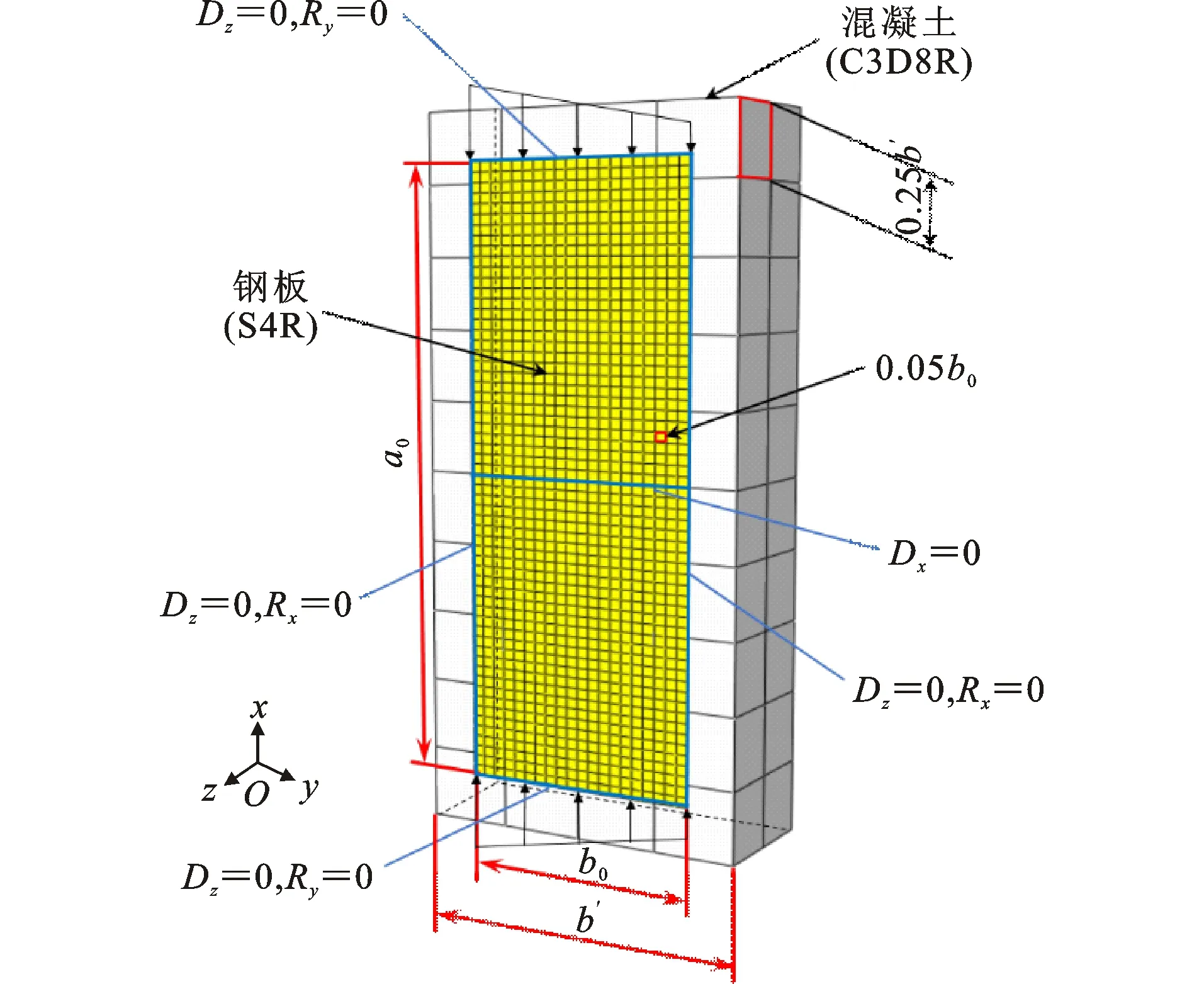
图3矩形钢管混凝土腹板非均匀受压有限元模型Fig.3Finite Element Model of RCFST Web Under Non-uniform Compression
钢板的边界条件为钢板4条边z方向的平动自由度、加载边绕y轴的转动自由度和非加载边绕x轴的转动自由度均被约束,为防止钢板加载时滑动,钢板中间高度截面x方向的自由度也被约束。对板件顶部和底部施加z=0平面内x方向上荷载大小线性变化的梯度荷载。
由于混凝土与钢板间存在接触问题,同时钢板还会因为屈曲存在大变形问题,用ABAQUS/Explicit求解存在上述问题的模型比用ABAQUS/Standard更容易收敛,在一定的加载速率下,显示动态求解的结果接近静态分析的结果,故本文采用该显示动态求解的方法对单侧约束平板的非均匀受压屈曲行为进行了有限元模拟。
混凝土对钢板的侧向约束和钢板屈曲时脱离混凝土表面用如下方式模拟:使用“Surface to Surface(Explicit)”接触并在法线方向选定“硬”接触,接触面切向选定“无摩擦”。为使钢板压弯变形后有足够的约束平面,混凝土板的长宽设置为钢板长宽的1.3倍,混凝土的网格尺寸为混凝土板宽的25%,钢板网格尺寸为钢板宽的5%,按上述网格尺寸划分可以同时保证结果的准确性与计算效率[6]。
有限元模型的参数应力梯度α为0~2,长宽比β为0.4~5.0,宽厚比b0/t为30~100。
1.2.2 弹性屈曲系数
图4为长宽比β=3,应力梯度α分别为0、1、2时钢板屈曲时的面外位移。板件屈曲波中点的面外位移与边缘荷载σ1的关系曲线如图5所示。面外位移开始急剧增长时的纵轴坐标即为此应力梯度下的弹性屈曲荷载σcr,将σcr代入式(1)即可得出非均匀受压单侧约束平板的弹性屈曲系数k。
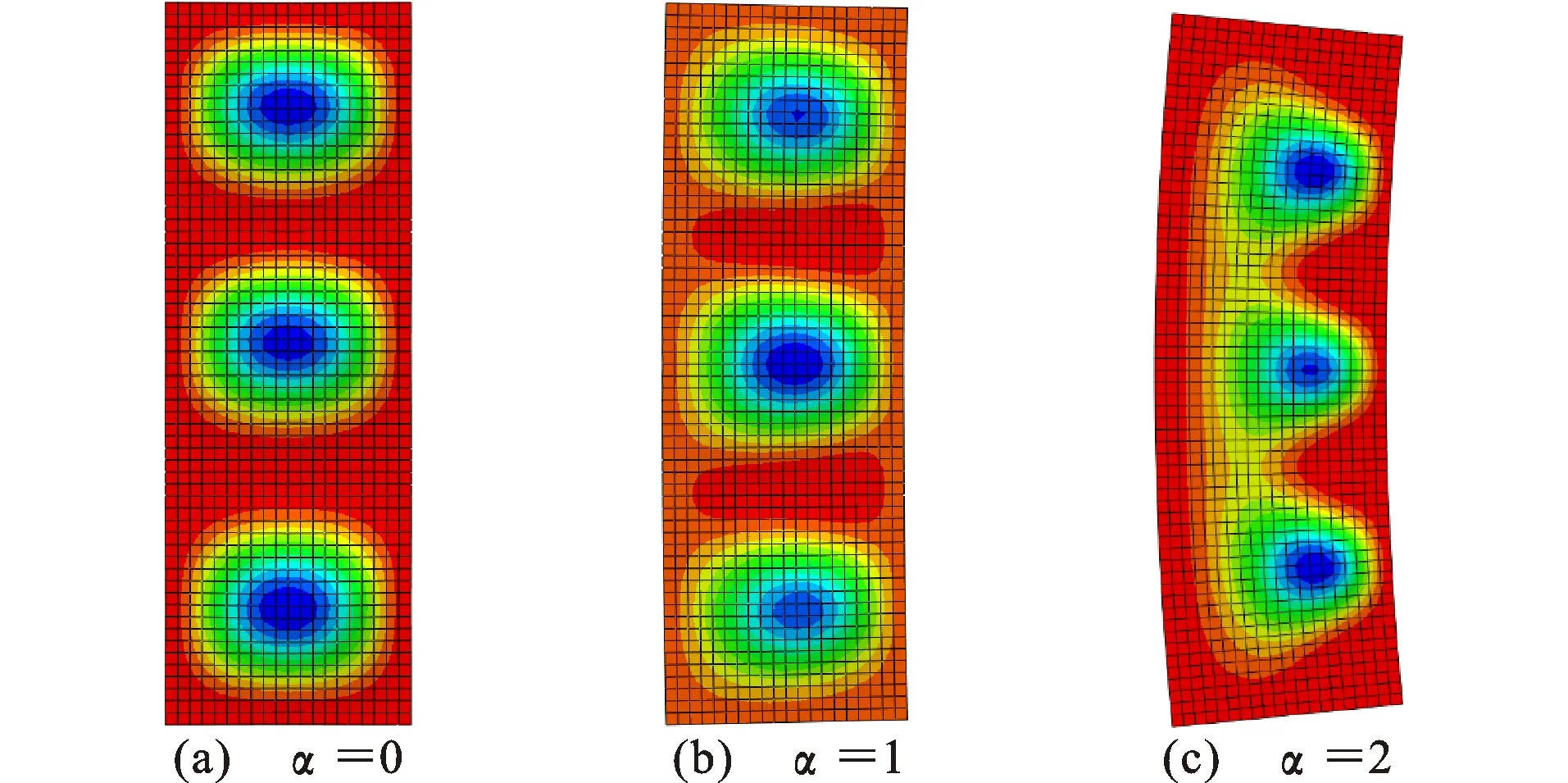
图4屈曲模态
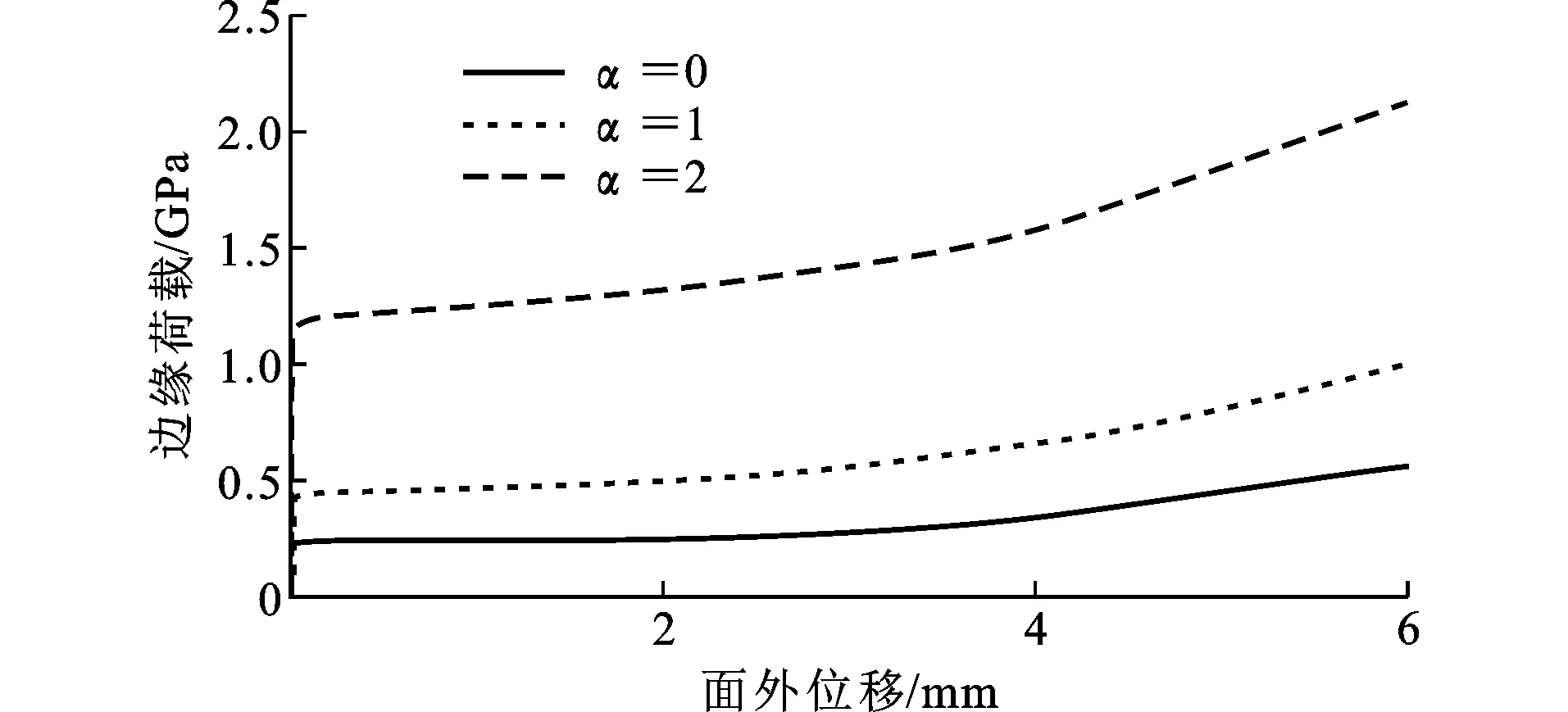
图5面外位移-荷载曲线Fig.5Out-of-plane Displacement-load Curve
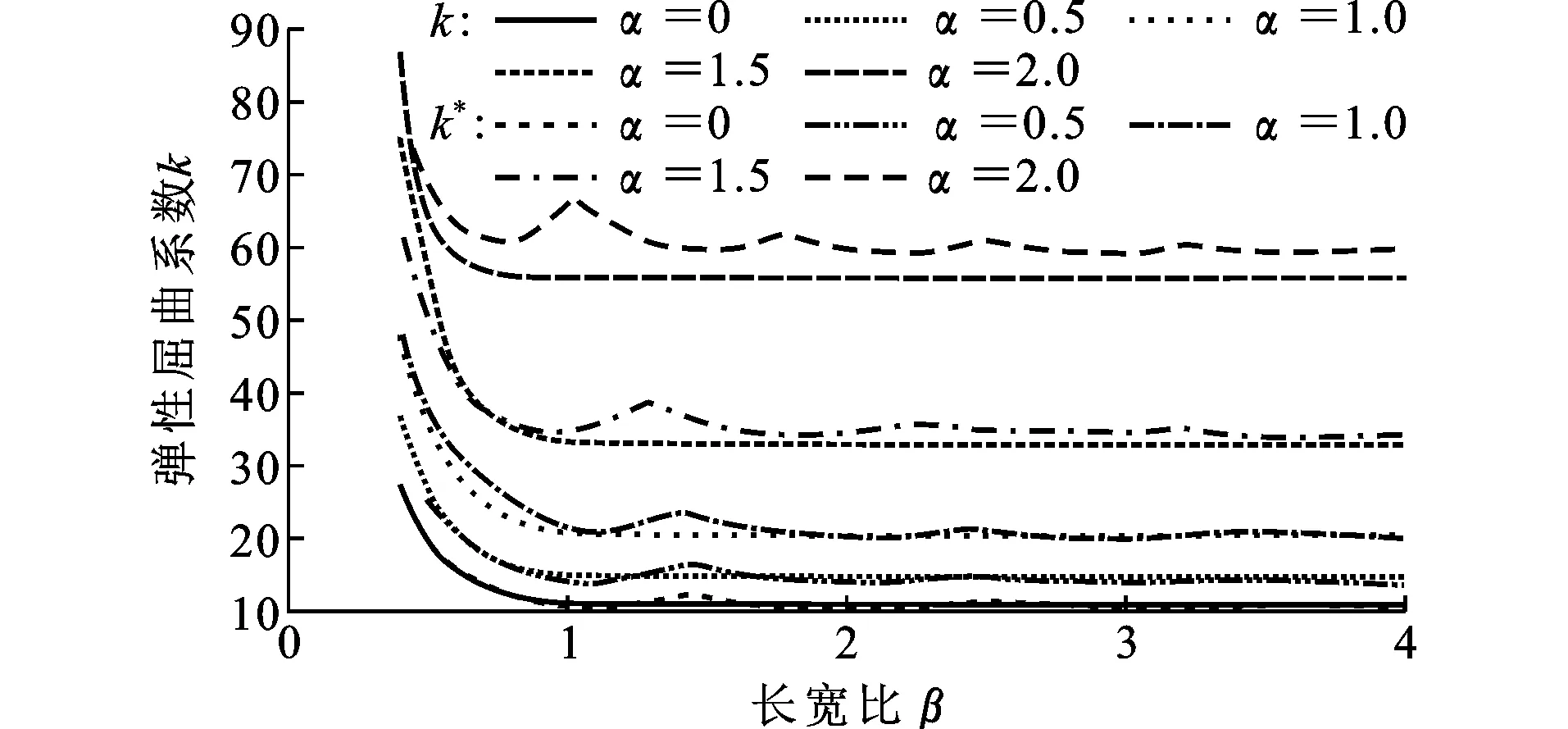
图6非均匀受压单侧约束平板弹性屈曲系数分布Fig.6Distribution of Elastic Buckling Coefficient of Unilateral Restraint Plate Under Non-uniform Compression
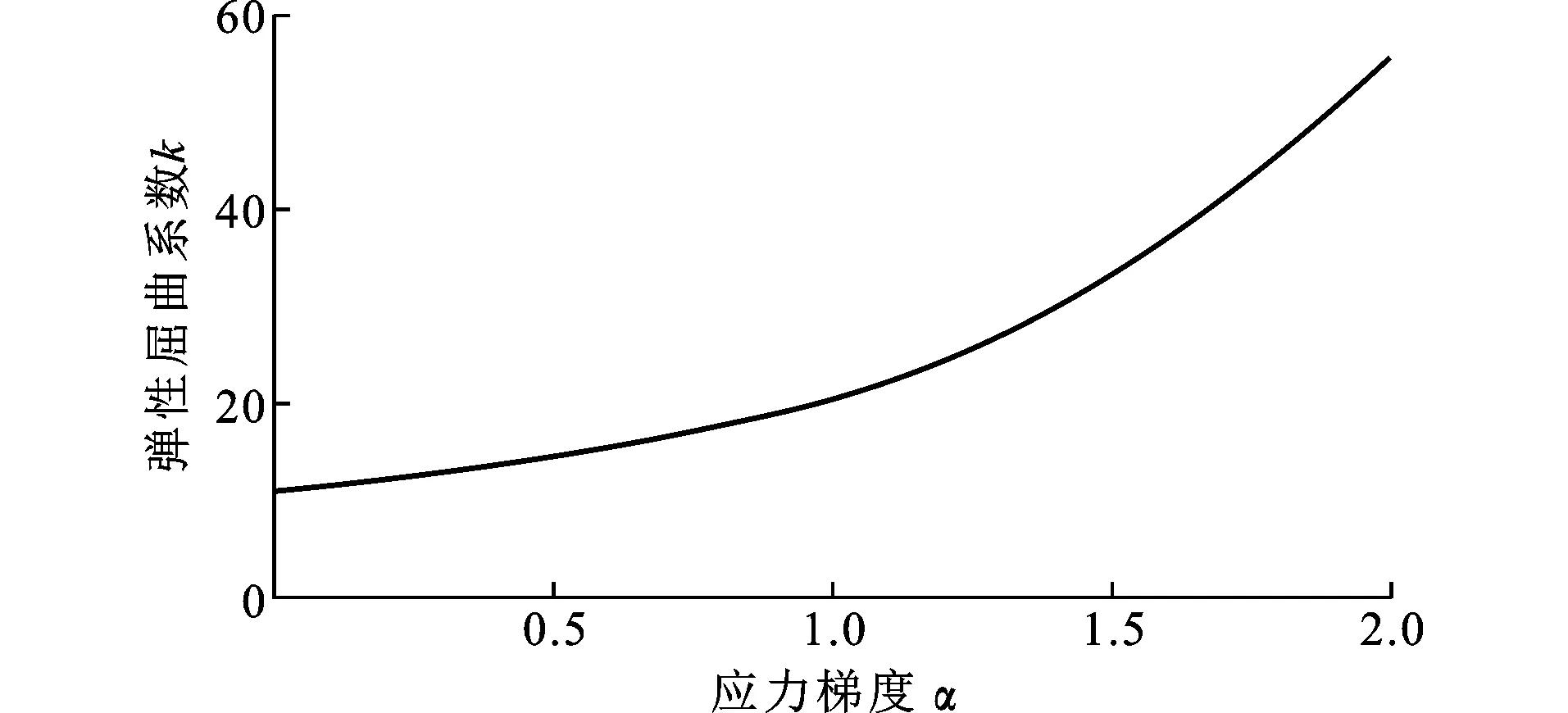
图7弹性屈曲系数与应力梯度关系Fig.7Relationship Between Elastic Buckling Coefficient and Stress Gradient
图7为长宽比β=3、应力梯度α在0~2范围内的弹性屈曲系数k的变化曲线。可以看出,弹性屈曲系数随着应力梯度的增大而增大,由轴压荷载时的10.96增加至纯弯荷载时的55.86。当加载边的应力梯度α<1.0时,弹性屈曲系数k随应力梯度的增大而提升的速度较为缓慢,但当加载边的应力梯度α>1.0时,由于板的加载边缘存在拉应力,延缓了横波的出现并使屈曲波的波峰出现在靠近受压的一侧(图4),从而有效提高了板抵抗局部屈曲能力,使弹性屈曲系数得到明显的提高。不同应力梯度下的弹性屈曲系数在长宽比β<1.2时随着长宽比的增大而明显减小,长宽比β>1.2时基本趋于稳定,实际工程中可以保守地取长宽比β>1.2时的弹性屈曲系数作为该应力梯度下弹性屈曲系数的取值,将不同应力梯度下的弹性屈曲系数参照中国规范GB 50018—2002[17]中的受压板件稳定系数公式进行拟合,得到单侧约束非均匀受压板的弹性屈曲系数计算公式,如式(2)所示。
(2)
(3)
W=b1h3/12+Bt3/6+Bt(h+t)2/2
(4)
A=b1h+2Bt
(5)
b1=2t+b0Ec/Es
(6)
式中:Ψ为应力梯度的另一种表述形式;N为截面承受轴力;W、A分别为钢管混凝土柱截面核心混凝土等效成钢后的抗弯惯性矩和截面面积;e为荷载偏心距;b1为按照混凝土和钢的应变-应力关系得到的混凝土等效为钢的截面宽度;B为钢管混凝土截面宽度;h为混凝土截面高度;Ec、Es分别为混凝土、钢的弹性模量。
由式(3)~(6)可知,钢管混凝土柱受力处于弹性阶段时腹板的应力梯度只与钢管混凝土柱截面尺寸和偏心距有关。
1.3屈曲模式
对于大宽厚比矩形钢管混凝土偏心受压柱,受拉侧混凝土先被拉裂失效,然后受压翼缘钢板局部屈曲,随后相邻腹板的钢壁板发生局部屈曲,屈曲波附近的混凝土由于失去钢板约束,先于其他截面的混凝土压碎,最终发生破坏[18]。按照钢壁板屈曲时钢材应力、应变所处的弹塑性阶段不同,可将钢壁板的局部屈曲分为塑性屈曲、弹塑性屈曲和弹性屈曲3种模式[6,19-20],可以通过正则化宽厚比λ的大小来确定钢壁板可能发生的局部屈曲模式,钢壁板的正则化宽厚比按式(7)确定[6]。
(7)
式中:fy为钢材屈服强度。
钢管混凝土柱中受混凝土约束的钢壁板屈曲问题中的塑性屈曲和弹塑性屈曲界限值λp可偏保守地取0.500,弹塑性屈曲与弹性屈曲板件的正则化宽厚比界限值λe取为1.348[6]。当λ<λp时,钢壁板发生塑性屈曲;当λp<λ≤λe时,钢壁板发生弹塑性屈曲;当λ>λe时,钢壁板发生弹性屈曲。
2偏压承载力计算公式
2.1基本假定
2.1.1 材料的强度假定
钢管应力-应变关系简化为理想弹塑性模型,不考虑应力硬化。根据极限平衡理论[21],矩形钢管混凝土偏压柱达到极限强度时,受拉区混凝土退出工作,受压区混凝土均匀受压。大宽厚比矩形钢管混凝土对核心受压混凝土的约束较弱,混凝土达到抗压强度后不会继续提高[7]。
2.1.2 钢管翼缘板和腹板的有效宽度
钢管混凝土偏压柱钢壁板的屈曲后强度计算采用Von Karman等提出的有效宽度理论。腹板与受压翼缘板使用有效宽度法的应力分布假定如图8所示。对于受压翼缘板,承受均匀压应力时,将中间部分因局部屈曲而发生承载力折减的部分视为失效部分,不承担压应力,而钢板在两侧宽度各为be/2的范围内,钢材应力均达到屈服强度,翼缘板的有效宽度be=ρfb,ρf为翼缘板有效宽度系数,b为受混凝土约束的翼缘板宽度。腹板在确定的偏心荷载下假定拉应力的部分都可达到屈服强度,而压应力的部分腹板应力分布按照受压翼缘的分布假定,腹板压应力部分有效宽度he=ρw(hs-t),hs为中和轴距受压混凝土上缘的距离,ρw为腹板有效宽度系数。本文的有效分布宽度系数ρ采用文献[6]中的适用于普通强度钢和高强钢,并区分弹性与弹塑性屈曲极限状态应力差异的单侧约束钢壁板的有效分布宽度公式,ρ取值为
(8)
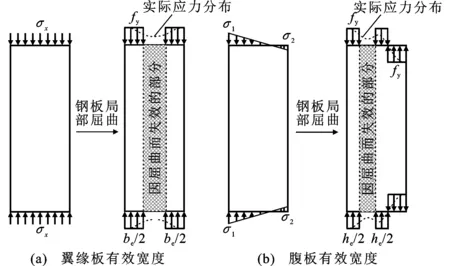
图8翼缘板与腹板有效宽度Fig.8Effective Width of Flange and Web
由式(8)可知,钢壁板的有效宽度与其正则化宽厚比λ有关,钢管的翼缘板和腹板的正则化宽厚比与弹性屈曲系数有关,翼缘板的弹性屈曲系数kf取10.96,而腹板的弹性屈曲系数kw与腹板的应力梯度α有关,按式(2)取值。
2.2轴力-弯矩相互作用方程
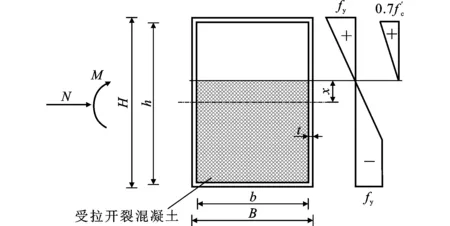
根据塑性中和轴的位置将轴力-弯矩(N-M)相互作用关系分两种情况讨论:中和轴位于腹板时,受力示意图见图9(a);中和轴位于翼缘板时,受力示意图见图9(b),其中H为钢管高度,“+”代表截面受压,“-”代表截面受拉,fck为棱柱体抗压强度标准值。
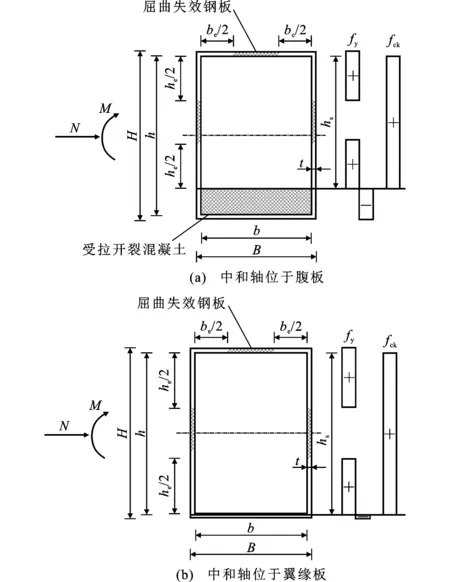
图9偏压荷载下截面受力示意图Fig.9Schematic Diagram of Cross-section Force Under Eccentric Load
2.2.1 中和轴位于腹板
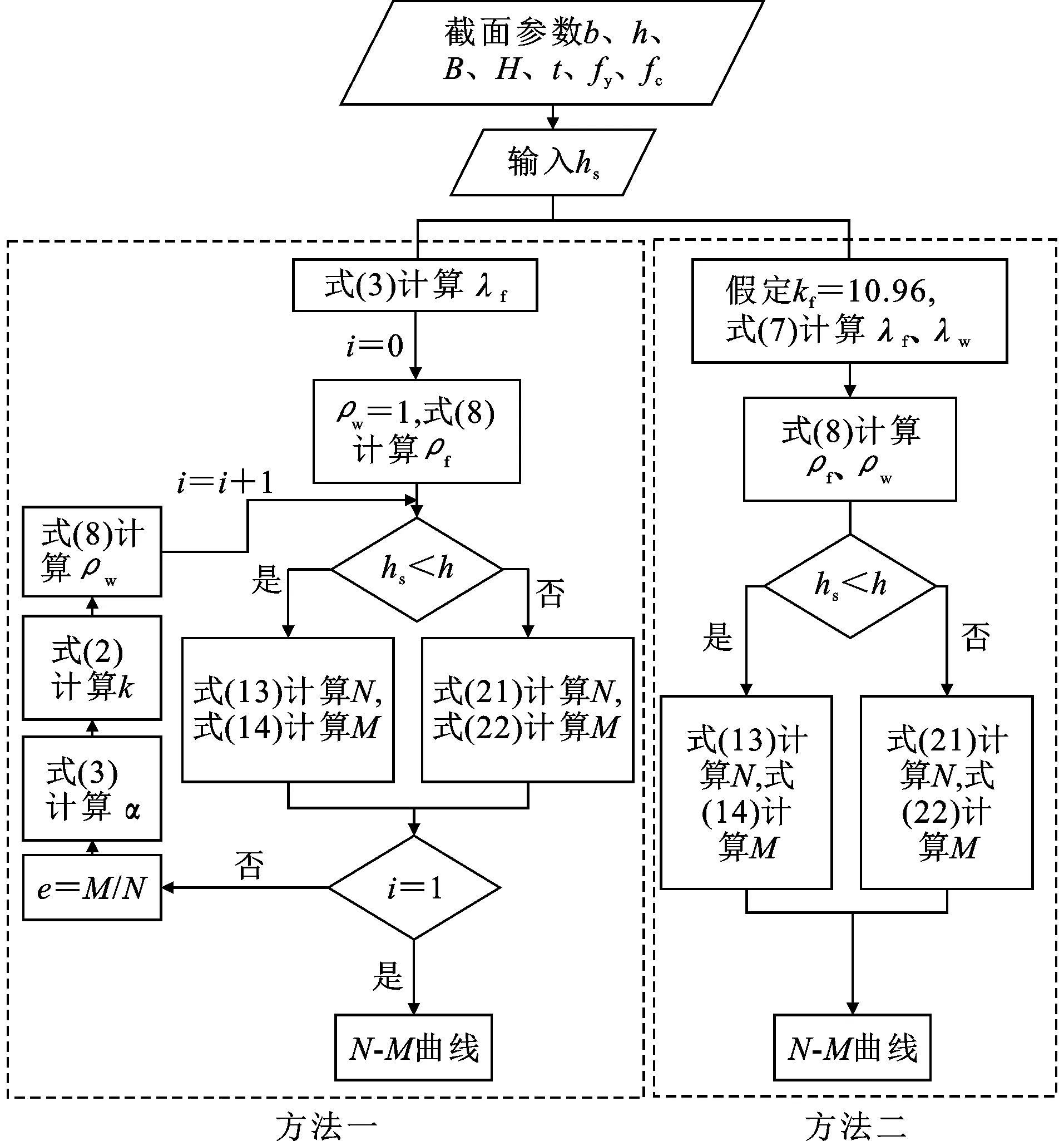
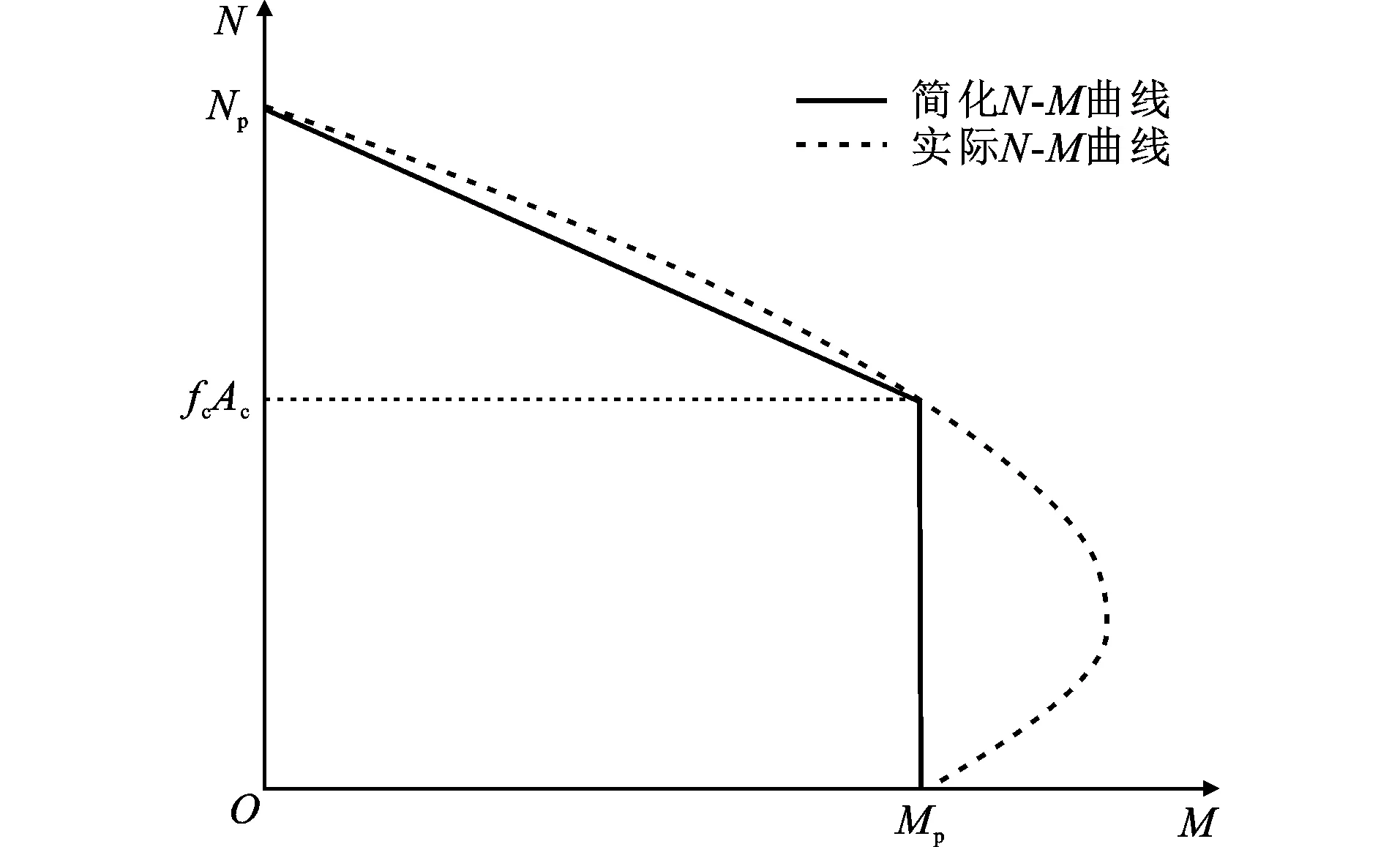
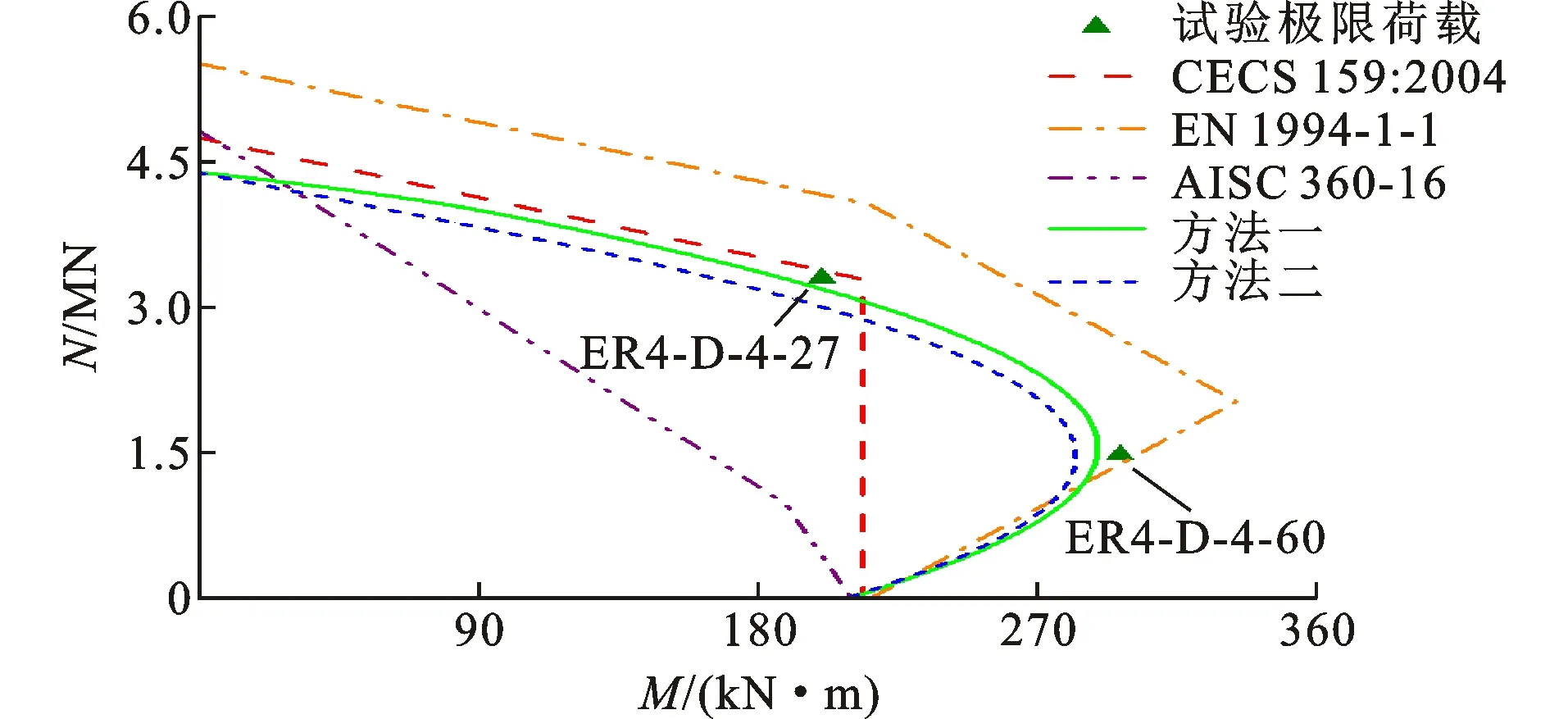
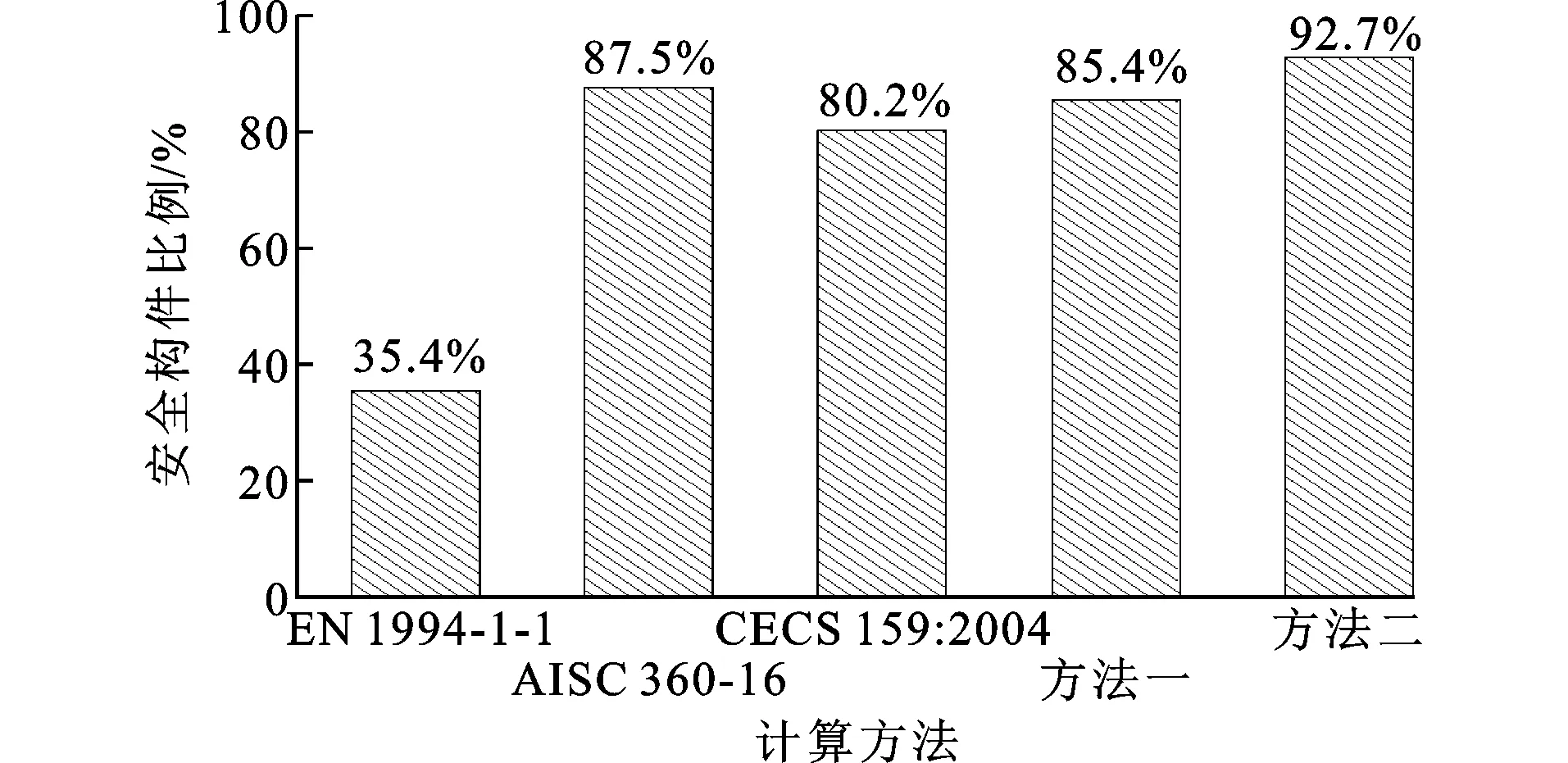
中和轴位于核心混凝土区域,即hs Ns=[2hs(1+ρw)t-2ht-(1-ρf)bt]fy (9) Nc=hsbfck (10) Ms={(h-hs)hs+(1+ρw)t+ 0.5(h+t)t[4t+(1+ρf)b]}fy (11) Mc=0.5(h-hs)hsbfck (12) N=hsbfck+[2hs(1+ρw)t-2ht-(1-ρf)bt]fy (13) M=0.5(h-hs)hsbfck+{(h-hs)hs(1+ρw)t+ 0.5(h+t)t[4t+(1+ρf)b]}fy (14) 式中:Ns为钢板承担轴力;Ms为钢板承担弯矩;Nc为混凝土承担轴力;Mc为混凝土承担弯矩。 由式(13)可得出中和轴的位置。 (15) 将截面轴力之和N=0代入式(15),可得出纯弯情况下中和轴的位置。 (16) 将式(16)计算的hs代入式(14)即可得到矩形钢管混凝土的纯弯承载力。 2.2.2 中和轴位于翼缘板 塑性中和轴位于钢管壁板内区域,即h Ns={2ρwht-(1-ρf)bt+ (hs-h)[4t+(1+ρf)b]}fy (17) Nc=fckhb (18) Ms={0.5[(hs+t)(h+t-hs)[4t+(1+ρf)b]}fy (19) Mc=0 (20) N=fckhb+{2ρwht-(1-ρf)bt+ (hs-h)[4t+(1+ρf)b]}fy (21) M={0.5[(hs+t)(h+t-hs)[4t+(1+ρf)b]}fy (22) 令式(21)中hs=h+t即可得到矩形钢管混凝土的轴压承载力,如式(23)所示。 N=fckhb+2(ρwh+ρfb+2t)tfy (23) 第2.1.2节仅给出了腹板有效宽度的分布模式,未给出ρw大小。腹板的有效宽度系数ρw需要通过偏心距e求得,但钢管混凝土偏压柱在从受力初期的线弹性阶段到破坏阶段存在受拉混凝土开裂和钢壁板屈曲后应力重分布等复杂情况,无法精确给出hs对应的偏心距e,也就无法得到ρw。因此本节提出了以下两种偏安全的腹板有效宽度ρw取值的假定,避开hs与ρw的精确对应关系,得到两种计算N-M相互作用曲线的方法: (1)方法一假定受压区腹板全截面有效,在给定hs后根据式(13)、(14)得出截面的M和N。由于偏心受压短柱加载时轴力和弯矩近似成比例增加,即M=Ne,将e=M/N代入式(3)、(4)得到腹板弹性屈曲系数kw,然后得到在给定偏心距下的ρw,将此ρw代回式(13)、(14)即可得出N-M相互作用曲线。由于最初假定腹板受压区全截面有效,且局部屈曲失效的部分靠近截面中心线,内力臂远小于翼缘板,所以在该假定下得出的偏心距要小于实际情况下腹板部分失效得出的偏心距,由式(2)、(3)、(7)、(8)可知,偏心距越小所得出的失效宽度就越大于实际情况的失效宽度,所以在该假定下得出的截面弯矩和轴力最终计算结果略小于实际截面的轴力与弯矩,故该假定偏安全。 (2)方法二假定腹板的有效宽度系数ρw取均匀受压板的有效宽度系数,则腹板的有效宽度系数不会随着荷载偏心距的变化而改变,hs在确定的范围内取值即可得出N-M相互作用曲线。由式(2)可知,在所有的梯度荷载中,承受均压荷载(α=0)的腹板弹性屈曲系数最小,由式(7)、(8)可知,弹性屈曲系数越小,壁板的有效宽度就越小,意味着屈曲后强度就越低。将任意屈曲荷载下的腹板有效宽度系数ρw取其均匀受压下的有效宽度系数,相当于不考虑腹板由均压荷载变为非均压荷载屈曲后强度的提高,是一种偏于安全的假定。 两种方法的计算流程如图10所示。 图10计算方法流程Fig.10Calculation Method Flow 本节采用收集到的试验数据,对不同规范及本文给出的偏压承载力计算公式进行对比,评价其适用性。 3.1.1 EN 1994-1-1规范 图11EN 1994-1-1计算方法示意图Fig.11Schematic Diagram of EN 1994-1-1 Calculation Method 图12EN 1994-1-1的N-M曲线Fig.12N-M Curve of EN 1994-1-1 3.1.2 AISC 360-16规范 AISC 360 Method-2(后文简称Method-2)为厚实截面的N-M曲线计算方法,与EN 1994-1-1规范类似,区别在于前者将混凝土的强度考虑了0.85的折减系数。AISC 360 Method-1为非厚实截面和柔薄截面采用二折线的计算方法(下文简称Method-1),仅需确定截面的轴压承载力Nn和纯弯承载力Mn就可以建立N-M相互作用方程(图13)。 图13AISC 360 Method-1的N-M曲线Fig.13N-M Curve of AISC 360 Method-1 两种截面的承载力分别有相应的计算方法: (1)若截面为柔薄截面,钢管混凝土柱钢壁板发生弹性屈曲,混凝土强度考虑0.7的折减系数,纯弯计算示意图如图14所示。轴压承载力Nn取为Ncr,按式(24)计算。 图14AISC柔薄截面计算示意图Fig.14Calculation Schematic Diagram of AISC Slender Section (24) (2)若截面为非厚实截面,钢壁板发生弹塑性屈曲,混凝土的强度在0.7~0.85间按宽厚比大小进行折减,Mn和Nn分别按式(25)、(26)计算。 (25) (26) (27) 式中:Mp、Np分别为非厚实截面与厚实截面的宽厚比界限值λp处对应的Mn和Nn,计算方法与厚实截面相同;My、Ny分别为非厚实截面与柔薄截面的宽厚比界限值λr处对应的Mn与Nn。 AISC非厚实截面计算简图如图15所示。 图15AISC非厚实截面计算示意图Fig.15Calculation Schematic Diagram of AISC Noncompact Section 3.1.3 CECS 159:2004规范 CECS 159:2004[24]关于偏压柱截面的N-M曲线的求解方法与EN 1994-1-1类似,为了方便设计,将实际的相互作用曲线简化为两折线,如图16所示。 图16CECS 159:2004的N-M曲线Fig.16N-M Curve of CECS 159:2004 为了验证本文所提出的大宽厚比矩形钢管混凝土短柱偏压承载力计算方法,从以往试验报告中搜集并整理了96个发生弹性屈曲或弹塑性屈曲截面的偏压试验数据,包括82个偏压试验数据和14个纯弯试验数据,见表1。偏压试件均为短柱,由于发生非塑性屈曲的钢板大都使用高强钢或具有大宽厚比,所以部分试件的宽厚比、钢材强度、混凝土强度突破了规范的限值,混凝土强度为圆柱体抗压强度。 利用第3.2节建立的矩形钢管混凝土短柱偏压试验数据库,用本文提出的大宽厚比矩形钢管混凝土短柱偏压承载力计算方法,计算数据库中构件的N-M曲线,并依据规范EN 1994-1-1、AISC 360-16、 CECS 159:2004计算出构件的N-M曲线做对比,EN 1994-1-1、AISC 360-16混凝土强度采用圆柱体抗压强度计算,CECS 159:2004与本文所提出的计算公式中的混凝土强度采用圆柱体抗压强度换算后的棱柱体抗压强度。 表1偏压试验数据Table 1Data of Eccentric Test 图17N-M相互作用曲线Fig.17Interaction Curves of N-M 定义强度因子S=Nexp/Ne,Nexp为试验偏心荷载承载力,Ne为各计算方法计算的极限偏心荷载,图18为各计算方法强度因子S分布图。图19为各计算方法安全构件比例(安全构件为S>1,即各计算方法得出的承载力不高于试验承载力的试件)。 图18各计算方法强度因子 图19安全构件比例Fig.19Safe Component Ratio 由图17和图18(a)可知,EN 1994-1-1规范计算出的截面承载力为最大的,随着正则化宽厚比的增大,有数量较多的试件的极限荷载低于按照EN 1994-1-1规范计算的极限承载力,因此它是最不保守的规范。原因是EN 1994-1-1规范假定钢材和混凝土都可以达到材料的极限强度,但数据库中部分试件的宽厚比超出规范适用范围,导致钢材发生弹塑性和弹性屈曲,使钢材无法全截面达到屈服强度。 由于AISC 360-16对混凝土的强度做了折减,其厚实截面承载力在用Method-2计算的时候比EN 1994-1-1要保守,且其非厚实和柔薄截面用Method-1的双折线模型计算承载力时体现出了过高的保守性(图17)。由图18(b)可知,试件的宽厚比越大,计算结果越保守,试件宽厚比小于并接近厚实截面与非厚实截面的界限宽厚比λp时,Method-2的计算偏于危险,但是当宽厚比大于这个界限时要换用Method-1计算,其计算结果又变得过于保守。AISC 360-16规范在宽厚比λp附近各构件的强度因子有较高的差异性,在宽厚比大于λp时AISC 360-16规范表现出了过高的保守性。 由于CECS 159:2004采用的混凝土抗压强度标准值是由棱柱体抗压强度确定的,对于相同的混凝土,其数值小于圆柱体抗压强度,因此其计算结果比EN 1994-1-1要保守(图17)。与EN 1994-1-1规范一样,部分试件的宽厚比超出了规范限值,使用该规范计算偏心距较小的大宽厚比试件时具有一定的危险性,如ER4-D-4-27试件,但其采用的简化双折线模型对偏心距较大试件做了保守折减,所以CECS 159:2004规范对发生大偏心破坏的试件(荷载偏心距大于双折线拐点处偏心距)承载力预测过于保守,如ER4-D-4-60试件。 由图17可知,由于腹板有效宽度的假定不同,方法一求得的截面承载能力略高于方法二得出的截面承载能力,方法一较为接近试验结果,但某些试件的承载力会介于方法一与方法二之间,造成了方法二的安全构件比例高于方法一(图19)。本文提出的两种方法在计算正则化宽厚比0.5~1.545的试件时均表现出较强的适用性。在计算采用高强钢、小宽厚比试件的偏压承载力时,其计算结果与各规范类似,当截面的正则化宽厚比较大时,由于该方法考虑了受压腹板和翼缘板的屈曲对钢板强度的折减,对EN 1994-1-1和CECS 159:2004中的钢板全截面屈服偏危险的假定进行了优化,同时又考虑了钢板屈曲后强度,相比于AISC 360-16过于保守的计算方法更加合理,所以其计算结果比其他规范要接近试件实际承载力。 本文推导的考虑翼缘板和腹板屈曲后强度的N-M曲线计算方法能够较为准确且略偏保守地计算大宽厚比矩形钢管混凝土柱偏压承载力。相比于EN 1994-1-1和CECS 159:2004,本文方法计算大宽厚比矩形钢管混凝土柱偏压承载力有更高的安全构件比例(图19),相比于AISC 360-16,其计算结果更加准确。方法二的安全构件比例是各计算方法中最高的(图19),与方法一相比,计算假定更容易理解,计算简单,且能准确地评估构件的偏压承载力,故本文推荐方法二作为大宽厚比矩形钢管混凝土短柱偏压承载力的计算方法。 (1)非均匀受压单侧约束平板的弹性屈曲系数k在长宽比β<1.2时随着长宽比的增大而明显减小,β>1.2时基本不变。在长宽比一定时,k随着应力梯度的增加而增加。提出的非均匀受压单侧约束平板的弹性屈曲系数计算公式,可用于有效宽度法计算非均匀受压单侧约束平板的屈曲后强度。 (2)各规范在计算大宽厚比矩形钢管混凝土偏压承载力时误差均较大:EN 1994-1-1规范未考虑钢壁板的屈曲,有75%的试件承载力进行了危险预估,是最不保守的规范;AISC 360-16规范在正则化宽厚比较大时对试件承载力进行了过于保守的估计,强度因子平均值为1.338,是各规范中最高的;CECS 159:2004规范也未考虑钢壁板的屈曲,对小偏心受压试件承载力进行了过高估计,其安全构件比例为80.2%。 (3)本文以非均匀受压单侧约束板件的弹性屈曲系数公式为基础,提出的基于壁板屈曲后强度的矩形钢管混凝土偏压承载力计算方法具有较高的计算精度,计算结果与试验结果吻合良好,方法一的强度因子平均值为1.111,方法二的强度因子平均值为1.085,方法二与方法一相比计算简单,相较于各计算方法能够准确地评估构件的偏压承载力,本文推荐方法二作为大宽厚比矩形钢管混凝土短柱偏压承载力的计算方法。2.3两种N-M曲线求解方法
3偏压承载力计算公式对比
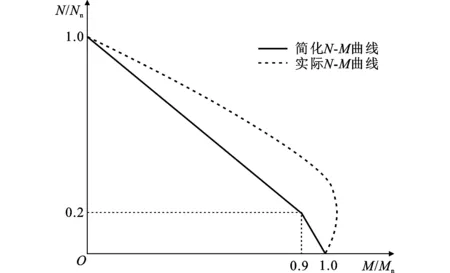
3.1规范中的N-M曲线

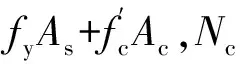

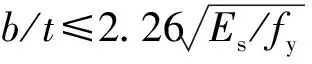
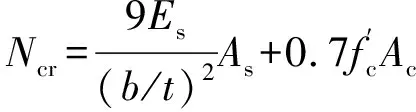
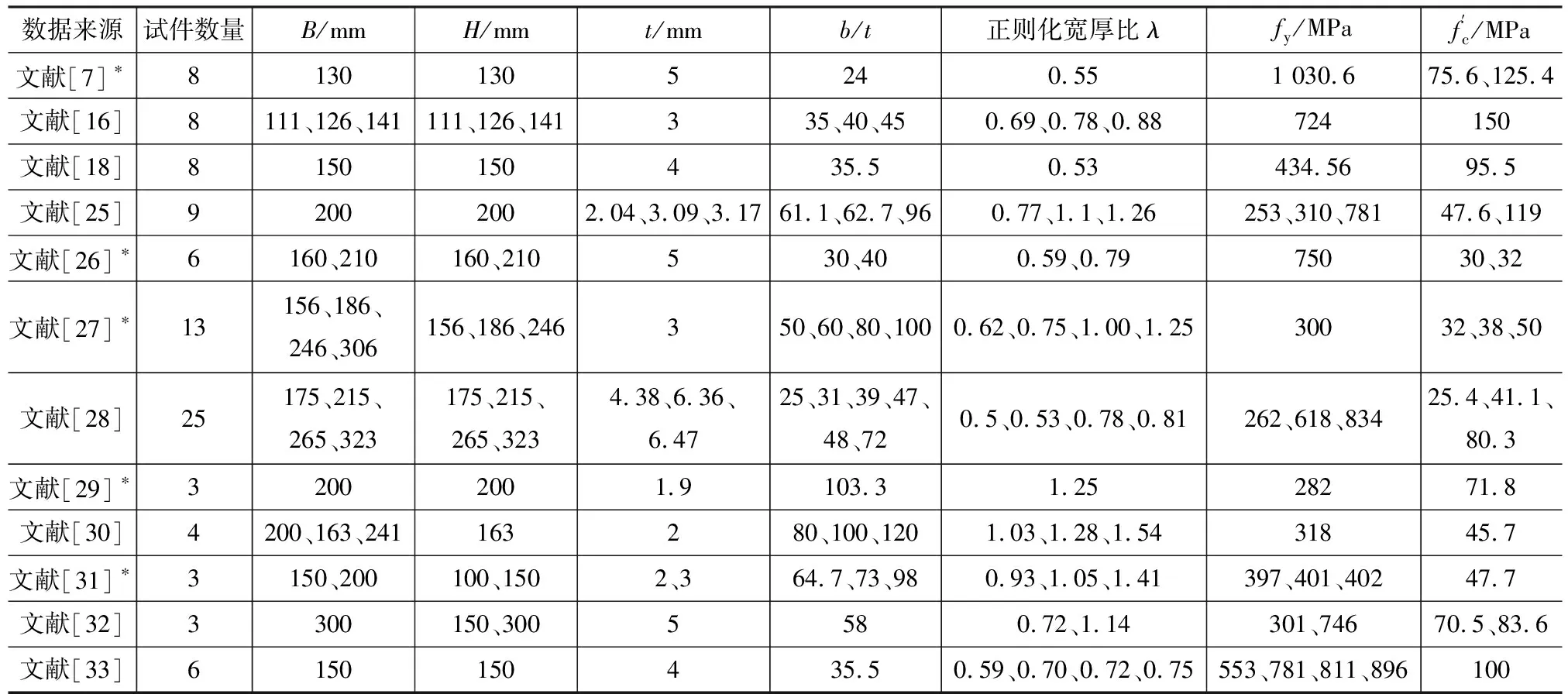
3.2大宽厚比矩形钢管混凝土柱偏压试验数据
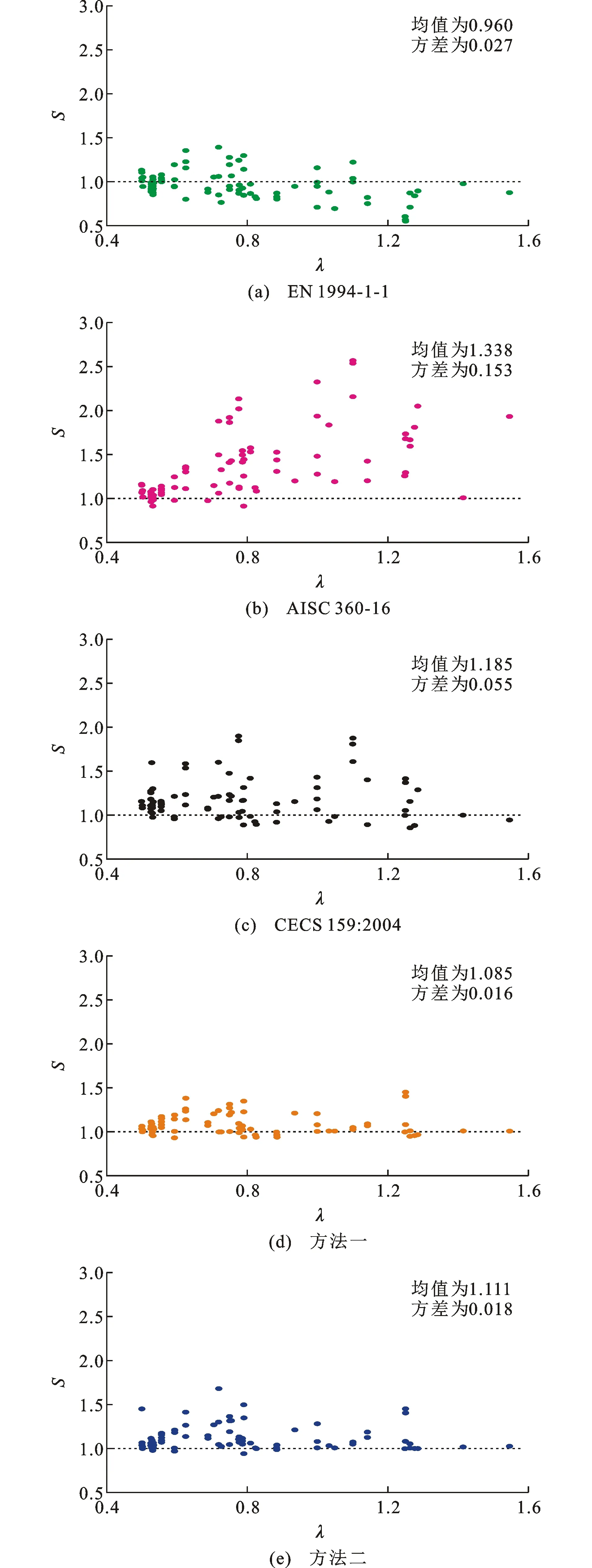
3.3对比与分析
4结语

