基于深度学习的高三专题复习教学微设计——以“同构法求数列通项公式”为例

肖 辉，吴 云

(南京市第十三中学，江苏南京，210008)

专题复习是高三数学教学的重要一环，某种程度上来说，专题复习的设计与教学实施决定了高考数学的质量.本文以“同构法求数列通项公式”为例，探讨高三二轮复习中基于深度学习的教学微设计.

1 教学过程

1.1 基础再现：在回顾中梳理知识

(1) 已知a1=1，an+1=an+1，则{an}的通项公式an=；

(2) 已知a1=1，an+1=2an，则{an}的通项公式an=；

(3) 已知a1=1，an+1=2an+1，则{an}的通项公式an=；

(4) 已知a1=1，an+1=an+n，则{an}的通项公式an=；

(5) 已知a1=1，an+1=an+2n，则{an}的通项公式an=.

设计意图：解题教学要遵循熟悉化、简单化、直观化原则，围绕模式识别实现转化和化归.本节课由基础题(1)(2)回忆等差、等比数列的定义，基础题(3)(4)(5)都是朝着“等差数列”“等比数列”方向转化，即“差”形式、“比”形式.

题(3)构造an+1+1=2(an+1)得到解决.一方面让学生感受同构式(结构相似，架构相同的式子)以及同构法，点明本节课主题；另一方面和学生一起归纳一般形式.

(板书1)an+1=pan+q⟹an+1+λ=p(an+λ).基础题(4)、(5)右边不是常数，可运用累加法来化解求和问题，为后面类似处理做铺垫.

我国著名的数学教育家徐利治先生曾经说过：“数学是模式的科学.”本组习题教会学生识别出基本模式，并熟练运用模式解决相关简单问题，教会学生遇到陌生的数列递推公式要有转化为“差”形式、“比”形式的意识.

1.2 似曾相识：在探究中训练思维

例1(1) 已知a1=1，an+1=2an+2n，求{an}的通项公式；

(2) 已知a1=3，an+1=2an+1-n，求{an}的通项公式.

设计意图：在数学学习里，联想可以将要研究的数学对象和有关的知识之间进行联系，由此及彼，找到不同对象和知识之间共有的规律.如问(1)与上面基础习题进行对比，产生联想，得到如下转化思路：

思路①，an+1=2an+2n⟹an+1=an+2n⟹“差”形式；

思路②，an+1=2an+2n⟹an+1=2an+1⟹“比”形式.

提问：思路①两式中an系数不一样，能否让左右两边系数转化一致？转化为“差”形式？找到同构式？思路②两式中相邻两项差不是常数，能否让两项的差转化为常数？转化为“比”形式？找到同构式？进一步探索发现有如下同构式：

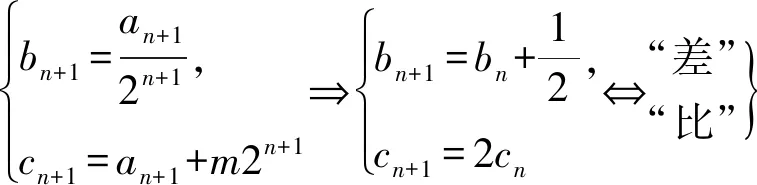
上面两组提问唤醒了学生的思维，激发学生从基本模式中进行类比联想，从解后反思中不断优化解题方法，不断增强学生洞察力和转化能力.波利亚说“数学问题的解决仅仅是一半，更重要的是解题之后的回顾.”很多看似风马牛不相及的习题，其实本质却是相通的.至此要引导学生重视解后反思，略去浮华，呈现本质，促进转化，有意识地训练学生数学思维.

由上面(1)的探究过程联想，引导学生发现(2)也可得到两种思路：

思路①，an+1=2an+1-n⟹an+1=an+1-n⟹“差”形式；

思路②，an+1=2an+1-n⟹an+1=2an+1⟹“比”形式.

提问：哪一思路更简单？后面遇到此情形优先选择哪一个？和学生一起归纳出一般形式：

(板书3)an+1=pan+an+b⟹an+1+λ(n+1)+μ=p(an+λn+μ)

令bn+1=an+1+λ(n+1)+μ，得到bn+1=pbn，从而将问题转化为“比”形式.学生在解题中遇到陌生的习题，生疏的知识，要认真观察、分析、联想，让新旧知识之间进行迁移，以发现知识间的共有规律，从而突破解题的障碍，打破解题的瓶颈，渗透数学核心素养的培养.

1.3 小试牛刀：在应用中培养素养

(1) 求证：数列{bn}是等比数列，并求其通项公式；

(2) 求{an}的通项公式.

教师深度引导、学生深度思考、学生深度参与、师生深度探究本例题，为深度学习进一步奠定了坚实的基础.

1.4 真题再现：在拓展中发展能力

例3(八省联考)已知各项都为正数的数列{an}满足an+2=2an+1+3an.

(1) 证明:数列{an+an+1}为等比数列;

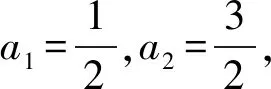
解题教学中，引导学生从不同角度、不同方向进行思考、联想，巧妙地运用迁移化归的数学思想方法，往往可以达到化繁为简、化生为熟、化隐为显、化难为易的效果，从而降低解题难度，快速找到解题突破口，真正掌握处理一阶、二阶递推公式的通用通法，在拓展中提升能力.

2 教学反思

2.1 教师的深度学习是前提

李善良教授认为，数学深度学习是为了学生核心素养发展的教学，是通过有深意的数学活动，让学生深度参与数学学习过程，深刻理解数学内容的本质和思想，实现数学与教材、教师、生活经验深度对话，培养学生质疑反思习惯和思维能力的教学.数学深度教学过程不是一个告知与接受的过程，而是一个交流合作、深度探究、质疑反思的过程，是一个发现问题、分析问题、解决问题的过程.深度学习是培养学生学科素养的重要途径，教师的深度学习则是前提.教师自身要对课标进行深度学习，深入了解学情，深入了解考情，深度细致备课，形成比较深度的数学思想体系.教师的教学设计要有层次化、系统化、结构化，教学中不断搭支架、不断给台阶、适当调控，提高学生的思维品质.

2.2 学生的深度学习是核心

用波利亚《怎样解题》中的思想，基础题是最能激发学生思考，是数学思维活动的切入点.本节课从“基础题型”开始，调动学生积极性；紧接着“似曾相识”引导学生通过类比和联想，打开思维，形成同构；“小试牛刀”更是基本模式的熟练运用，甚至一位同学当堂表示“早点上这节课，考试时就不会束手无策了”；最后八省联考的“真题再现”让学生不由体会到“看破迷雾”的恍然大悟.当然设计的问题也要符合学生的实际，要让学生处于“跳一跳，摘到桃”的状态，从而能持续驱动学生进行探究，激发思维.本节课中例1(1)中一连串的追问都会引起学生认知冲突，引发探究，驱动思维发展.本节课中，从开始的困境到同构法的形成，都是学生利用已有知识、方法、思想“同构”出来的，让学生充分从感性到理性、从特殊到一般中构建出一般方法，符合学生的认知规律，遵循了学生学习规律.

2.3 把深度学习的教学真正落实到课堂教学中

本文以“同构法求数列通项公式”的教学设计为例，通过类比学习、探究活动、创设冲突，帮助学生打开思维，深化自主建构方法的意识，提炼出建构新方法的一般策略，提升自主完善方法及反思的能力，提高认知能力和创新能力.从“深度学习”走向“深度教学”，深入推进基于核心素养的教学方式的改革，把基于核心素养的教学真正落实到课堂教学中，把深度学习的教学真正落实到课堂教学中，这样就把核心素养从抽象的理论变成看得见、摸得着的行动.笔者在本节课的设计上努力实践美国教育家苏娜丹戴克说过的一句话：Tell me， I will forget；Show me， I may remember; Involve me， I will understand.(告诉我，我会忘记；做给我看，我会记住；让我自主参与，我会完全理解.)