基于logistic回归的连续型解释变量离散化方法效果比较
何贤英
郑州大学第一附属医院互联网医疗系统与应用国家工程实验室,450052 河南 郑州
多因素回归分析在医学领域中具有广泛的应用,无疑已成为医学研究者的得力工具。在影响因素识别、影响程度量化的相关医学研究中,通过对连续型解释变量离散化后构建回归模型十分常见。连续型变量转变为分类变量后,被分到同一组内的个体被视作具有相同的概率风险[1-2],选择不同的界点将导致不同的分析结果,分界点选择有误甚至可能得出影响因素和结局之间虚假的联系。因此,如何客观合理地选择分界点对连续型解释变量进行分类,最大程度地区分出高风险组和低风险组,充分利用连续型解释变量提供的信息是多因素回归研究中面临的问题之一。本研究以logistic回归分析为例,针对自变量和结局变量为非线性变化关系时,提出连续型解释变量离散化的有效解决方法,其他类型的多因素回归分析可以此类推。
1 原理和方法
1.1 模拟数据产生
本研究以病例对照研究为研究背景,模拟产生服从正态分布的连续型自变量“年龄”。选取效应量作为关键指标,以控制自变量和结局变量之间发生假阳性的情形。效应量是指由于因素引起的差别,表示不同处理下的总体均值之间差异的大小,可以在不同研究之间进行比较,是衡量处理效应大小的指标[3-5]。
1.1.1 不同效应量下单自变量非线性数据的产生
设定病例组和对照组的“年龄”(age)均服从正态分布,控制2组的标准差取值不同,依次增加病例组和对照组均数的差值,从而使效应量的大小从0.1依次增加到0.6,产生模拟数据集A1~A6。
在模拟数据A分析的基础上,固定效应量取值为0.5,分别产生二分类自变量X1、X2、X3,设定X1、X2、X3和结局的关联系数分别为0.0、0.3、0.5,从而控制进入回归方程的自变量。与此同时,产生服从正态分布的连续型自变量X4、X5,其中X4的病例组和对照组均数效应量为0.0,X52组均数效应量为0.5。通过上述方式产生模拟数据集B1。
1.1.3 不同样本取值下单自变量非线性数据的产生
设定病例组和对照组的“年龄”(age)均服从正态分布,控制2组的标准差取值不同,固定效应量取值为0.5,依次增加病例组和对照组的样本量,分别取值为200、500、1 000、2 000、5 000,从而产生模拟数据集C1~C5。
1.2 资料非线性判断方法及其预处理
本研究采用“SemiPar”软件包中的半参数回归模型,根据自由度是否大于2对连续型自变量和logitπ之间是否满足线性关系进行判断[6]。SmeiPar包中的半参数回归模型是一种使用了2m-1次样条平滑的混合模型,其一般表达式为
1.3 连续型解释变量离散化的4种预处理方法
拟合logistic回归模型时,分别采用目前常用的离散化方法原始变量法、中位数法、单界点P值最小法及本研究提出的双界点OR值最大法对原始数据进行预处理,具体的离散化方法实现过程如下[7]:
1)原始变量法:原始数据不做处理,直接纳入回归模型。
2)中位数法:以中位数为分界点,将连续型自变量转化为二分类变量。
例如,在对幼儿的行为习惯进行培养的过程中,我们可以结合幼儿的性格特点,对一些在日常生活中不好的习惯加以指出,并向幼儿解释这些习惯在生活中可能带来的影响等。之后,我们还要及时与幼儿一起,以相互约定的方式制定一些简单又便于实施的规则,让幼儿对这些“约定”能够有一个较为深入的体验。而为了避免幼儿自觉性薄弱所造成的忘记遵守这些规则,我们可以在班级中张贴图片或可爱的艺术字体来达到对幼儿的一个警示或提醒的作用,让幼儿在这种人性化的管理服务中,逐渐养成正确的行为习惯,使精细化管理在精确到幼儿这一主题时的价值得以充分体现。
3)单界点P值最小法:以自变量的每一个取值作为潜在分界点(排除前后20%的自变量取值),对原始数据进行二分类,选择P值最小的自变量取值作为分界点。
4)双界点OR值最大法:根据概率风险相同的原则,将大于下侧界点和小于上侧界点的个体划分为高风险组,两端个体划分为低风险组,选择OR值最大的上下界点作为自变量取值的分界点。
1.4 模型拟合效果评价
模型效果的评价主要考虑三方面的内容,模型的拟合优度、判别能力、变异的解释程度。其中拟合效果的评价采用-2 log likelihood和最小信息准则,即AIC准则(akaike information criterion);判别能力采用正确合计率进行评价;变异程度的解释采用NagelkerkeR2系数进行评价。
2 模拟实验结果
2.1 不同效应量下单自变量模型拟合结果
对模拟数据集A1~A6采用半参数回归模型拟合得到自变量和logitπ的函数关系,见图1。其中A1~A6自由度(df)均大于2,说明自变量和logitπ不满足线性关系。

图1 模拟数据集A1~A6自变量和logitπ的函数关系图
分别采用连续型变量法、中位数法、单界点P值最小法、双界点OR值最大法分类后拟合logistic回归模型所得AIC见图2。模拟研究A1~A6可见,对于自变量和logitπ为非单调变化关系的数据,基于OR值最大化的分类方法均能更好地捕捉到与结局有关联关系的影响因素,模型拟合效果最好。
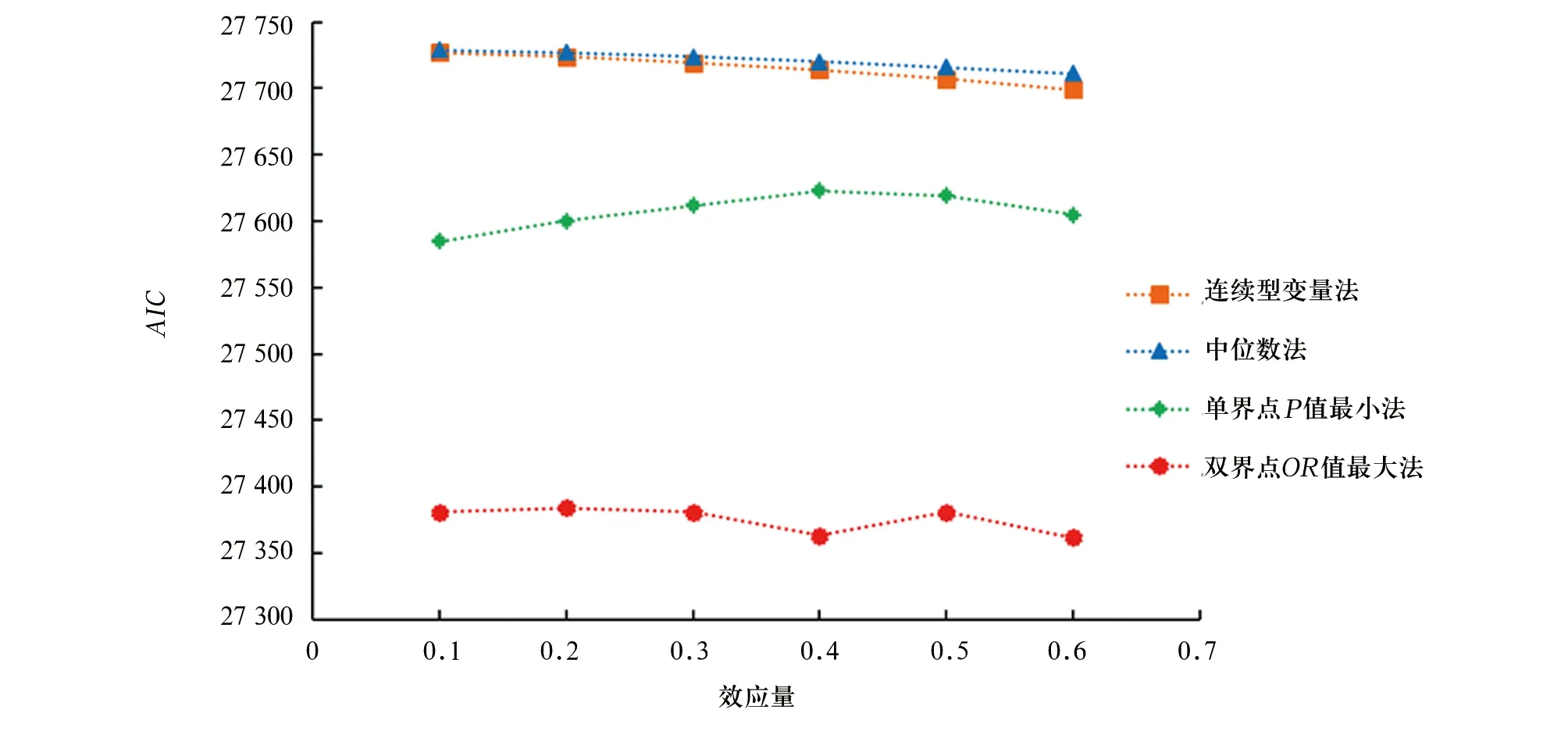
图2 4种方法拟合logistic回归模型的AIC变化情况
2.2 固定效应量下多自变量模型拟合结果
模拟数据集B1采用半参数回归模型拟合结果见图3。由图3可以看出自变量age和logitπ之间不满足线性关系(df=4.773),自变量X4、X5和logitπ之间满足线性关系(df=1)。
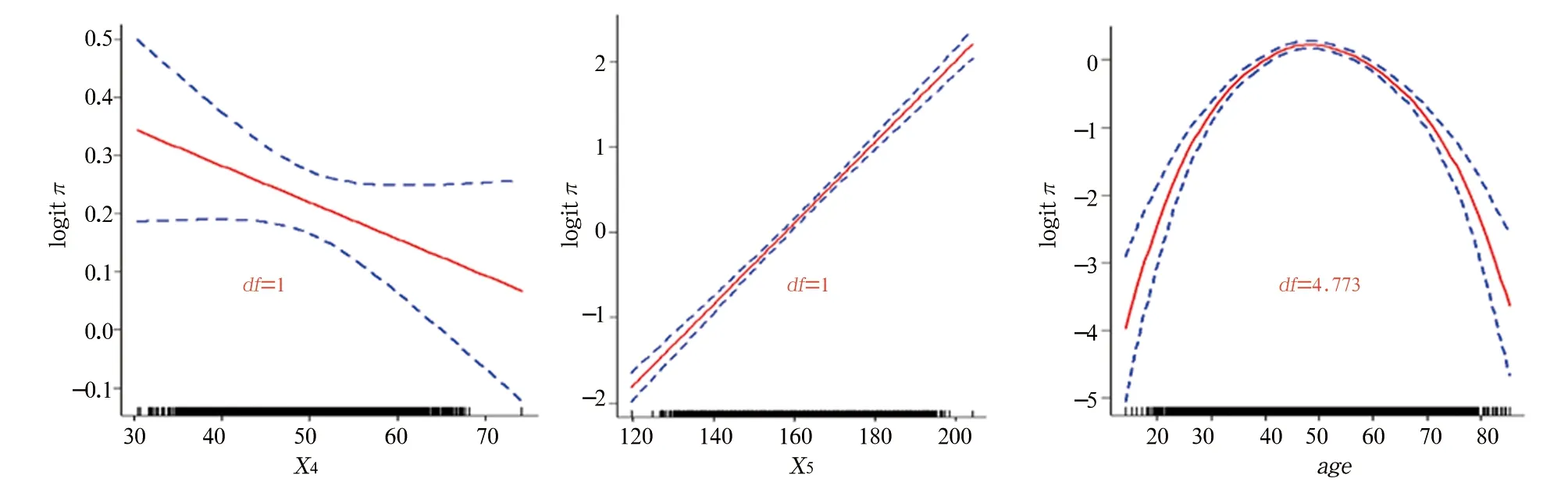
图3 模拟数据集B1自变量和logitπ的函数关系图
采用4种方法处理后的数据拟合logistic回归模型信息见表1。表1显示中位数法纳入的自变量为X2、X3、X5,连续型变量法、单界点P值最小法、双界点OR值最大法除纳入这3个变量外还纳入了自变量年龄。

表1 模拟数据B1拟合logistic回归模型信息汇总表
不同处理方法模型拟合logistic回归模型效果比见表2。由表2可知双界点OR值最大法模型拟合效果最好,表现在其AIC、-2 log likelihood值最小,NagelkerkeR2最大,正确合计率、灵敏度和特异度也较高。由此结果可见,基于OR值最大化的分类方法能更好地捕捉到与结局有关联关系的影响因素,且模型拟合效果均比目前常用的分类法好。

表2 不同处理方法模型拟合效果比较(模拟数据B1)
2.3 不同样本取值下单自变量模型拟合结果
设定病例组和对照组的效应量取值为0.5,选取不同的样本量200、500、1 000、2 000、5 000,并采用4种处理方法拟合logistic回归。见表3。
在样本量取值为200、500、1 000及2 000时连续型变量法和中位数法均没有筛选出有意义的自变量“年龄”,而单界点P值最小法和基于OR值最大化的分类法自变量“年龄”均有统计学意义。当样本量为5 000时4种方法筛选出的自变量“年龄”均有统计学意义,但是OR值最大化的分类法模型拟合效果最好,表现为AIC取值最小。见表3。

表3 (续)
3 讨论
在医学研究中研究者从临床应用及统计分析的角度考虑,经常将连续型自变量转变为二分类变量进行分析[8]。从临床应用的角度考虑,二分类自变量的优势在于:1)提供了简单的风险分类方法,比如高风险组和低风险组;2)有助于建立前瞻性研究的适宜标准;3)协助选择治疗建议;4)设定疾病的诊断标准;5)估计疾病的预后;6)施加一个假定的生物学阈值等[9-13]。从统计学的角度考虑,二分类自变量的优势在于:1)从统计模型方面提供了关于效应更为简单的解释方法,比如logistic回归模型中的OR值及Cox回归中的RR值;2)不需要考虑一般常用统计模型中连续型自变量和结局之间需满足线性这一前提条件;3)可根据事先假定的阈值效应建立模型;4)在研究中收集连续型自变量需要更高的经济成本,并且质控不严时,数据的可靠性也难以保证,所以分类数据能提供更有效的信息[14-18]。
针对多因素回归分析中连续型自变量离散化的处理方法,国内外有不少学者进行了有益的尝试[19-20]。目前对于连续型变量转变为分类变量的方法主要从2个角度考虑[8]。第一,基于数据的分类方法,如以特定的百分位数、均数、临床参考界值等进行分类。目前,较为常用的分类方法为中位数法[20],该方法以中位数为界将连续型自变量分为低风险组和高风险组。第二,基于结果的分类方法,该方法将自变量的每一个取值都作为可能的潜在分界点,对所有潜在界点分类分析并比较分析结果,以一定的评价标准,选择最佳的分界点,最为常用的为单节点P值最小法。上述分类方法会导致具有相同(或相近)的概率风险的研究个体被分到不同的组,从而使高、低风险组比较时部分风险抵消。本研究以OR值最大化作为寻找分界点的判定标准。因为OR值不仅能反映自变量和结局有无关系,同时能够充分概括这种联系的强弱;当筛选多个影响因素时,可以根据OR值的大小排序,对应于各影响因素的风险高低。通过对比研究证实,当自变量和logitπ为非单调变化关系时,基于OR值最大化的分类方法能更好地捕捉到与结局有关联关系的影响因素。与其他3种方法相比,双界点OR值最大法能够更合理地量化自变量和结局之间的联系,且模型的拟合优度、变异的解释程度均比目前常用的连续型变量法和中位数分类法效果好。
冯国双等[21]对logistic回归模型构建过程中容易忽视的几个问题做了系统阐述,指出现有相关研究在研究资料前提条件判断时存在2个主要问题:缺乏连续型解释变量和logitπ之间是否满足线性关系前提判断及样本量不足。本研究以效应量作为关键指标,采用半参数模型判断验证自变量和结局变量之间的非线性关系,证明了在回归模型的构建过程中,应首先判断连续型解释变量和结局变量之间的函数关系。通过研究结果分析,本研究推荐在实际研究工作中采用半参数回归模型,探索表现为未知函数形式的自变量和结局变量之间的函数关系。Wand等[22]于2003年对半参数回归模型进行系统描述,并形成了R软件包SemiPar用于半参数回归模型分析[6]。拟合logistic回归模型时,先对连续型自变量和结局变量拟合半参数回归模型,能够更清楚地了解自变量与结局之间的真实风险关系,便于后续选择适宜的数据处理方法。本研究根据不同离散化方法获得的模型拟合效果指标AIC值,说明连续型解释变量离散化方法的选择对于多因素回归模型的结果解释至关重要。
本研究的局限性在于仅探讨了连续型自变量离散化为二分类自变量的情况。而在医学研究的领域中,对连续型自变量进行多分类也非常普遍。可以在本研究的基础上,继续研究当连续型自变量离散化为多分类自变量时,适宜分界点的确定方法。与此同时,本研究仅模拟了当一个连续型自变量和logitπ之间不满足单调变化关系时,如何将其离散化为二分类自变量的情况,对于多个连续型自变量和logitπ之间呈现非单调变化关系时,如何寻找合适的分界点进行分类有待一步的研究。

