基于R语言的ARIMA模型在医院平均住院日预测中的应用

郭在金 周罗晶

1 扬州大学公共卫生学院，225009 江苏 扬州； 2 江苏省苏北人民医院管理研究所，225001 江苏 扬州

如何降低平均住院日，不断优化卫生资源配置，提升医院运行效率，既是现代医院管理制度的要求，也是医院管理者必须充分重视和着力解决的问题之一。因此，对医院平均住院日进行科学预测，可以为合理配置医疗资源，提高医疗服务质量和医院精细化管理水平提供科学依据。差分自回归滑动平均模型(autoregressive integrated moving average model，ARIMA)是一种经典的时间序列分析方法，可以较好地获取时间序列中的线性特征以及周期性和趋势性，被广泛地应用于传染病预测[1]、卫生资源预测[2]等方面，预测效果较为准确，并且在平均住院日预测方面也有较好的应用[3]。本研究利用江苏省某三甲医院的平均住院日逐月数据构建ARIMA模型，对医院的平均住院日进行预测，为医院医疗资源的优化配置提供参考。

1 资料和方法

1.1 资料来源

通过江苏省某三甲医院的数据中心，获取2013年1月至2022年5月共113个月的逐月平均住院日数据。其中2013年1月至2021年6月的数据作为训练集建立模型，2021年7月至2022年5月共11个月的数据作为验证集验证模型。

1.2 方法

ARIMA模型最早由美国统计学家Box和Jenkins于1972年提出[4]，是时间序列中预测精度相对较高的一种模型，其由自回归AR和移动平均MA组成。AR表示根据自身的滞后值或先前值进行回归，MA则是依据时间序列资料，逐项推移，依次计算包含一定相数的序时平均值。ARIMA模型包括不具有季节性的ARIMA(p，d，q)和具有季节性的ARIMA(p,d,q)(P,D,Q)s，其中，p、d、q分别是自回归阶数、差分次数和移动平均阶数；P、D、Q则是具有季节性的自回归阶数、差分次数和移动平均阶数；s是季节周期。ARIMA模型的原理是将预测值由过去数值和随机误差的线性函数来表达[5]。

ARIMA模型主要包括以下步骤：①数据的预处理，首先确定时间序列是否为稳定的平稳时间序列，如果为非平稳时间序列则要通过差分或数据转化使其变为平稳的时间序列。②模型的识别与选择，通过绘制自相关系数图(autocorrelation function，ACF)和偏自相关系数图(partial autocorrelation function，PACF)来确定备选模型的参数p、q；P、Q的确定一般是通过高阶到低阶逐个尝试，还可以通过R语言中auto.arima函数来确定多个备选模型，最后通过赤池信息准则(AIC)和贝叶斯信息准则(BIC)最小原则来确定最佳模型。③模型的参数诊断，通过Ljung-Box检验对模型进行白噪声检验，判断残差是否满足白噪声序列，检查残差是否独立且正态分布，从而验证所建立序列模型的充分性。在模型建立后，通过MAPE(平均相对误差)和RMSE(均方根误差)来评价模型的拟合程度，其值越低表示拟合效果越好。

1.3 统计学方法

本研究使用Excel 2016建立数据库，应用R 4.1.3软件进行统计分析，建立ARIMA模型。检验水准α双侧=0.05。

2 结果

2.1 时间序列图

绘制2013年1月至2021年6月该院平均住院日逐月时间序列图，并对时间序列进行趋势性、季节性、周期性分解。observed为该院平均住院日值，trend是序列的趋势性，由trend处可见该院平均住院日整体上呈现下降的趋势，seasonal处可看出该序列有一定的周期性。用adf.test函数对原始序列进行ADF检验后，Dickey-Fuller值为-2.32，P=0.44，提示该序列为非平稳时间序列，需要进行差分。见图1。

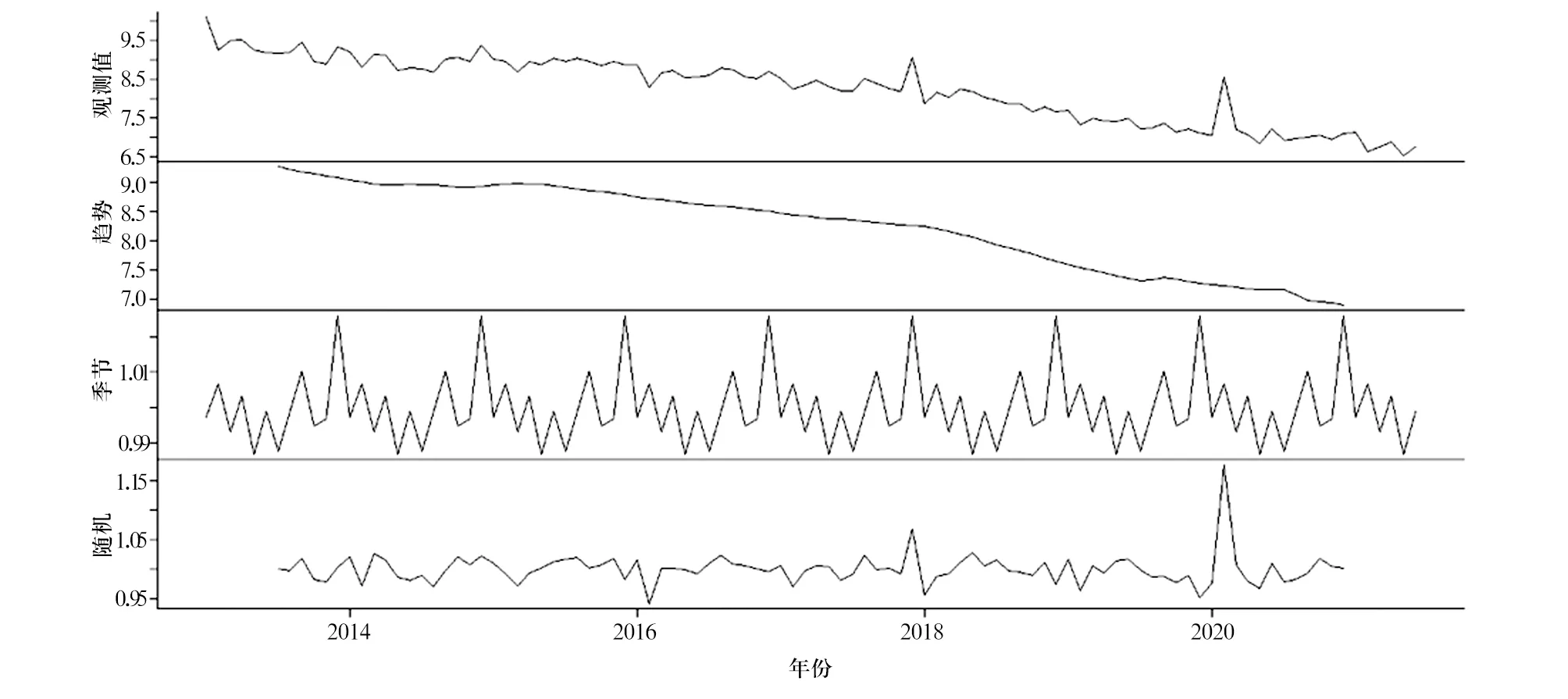
图1 2013年1月至2021年6月该院平均住院日时间序列分解图

2.2 时间序列的平稳化

原始时间序列为非平稳的时间序列，并且具有一定的周期性，因此需进行季节性差分。经1阶12步季节性差分后(d=1，D=1,s=12)，再进行ADF检验，Dickey-Fuller值为 -6.26，P<0.01，提示差分后的序列为平稳的时间序列。差分后的序列中，原序列的季节性趋势被消除，初步判断该模型的参数为ARIMA(p,1,q)(P,1,Q)12。

2.3 模型的识别与诊断

对差分后的数据绘制ACF图和PACF图，见图2、图3。由ACF图可以看出，自相关系数在一阶后截尾，而偏自相关系数图拖尾，同时结合R语言中的auto.arima函数，寻找最佳参数，最终确定p=0，q=1。而对于季节性的参数P、Q而言，根据文献[6-7]，不会超过2，一般是通过从高阶到低阶逐个尝试，根据赤池信息准则(AIC)和贝叶斯信息准则(BIC)最小原则来确定最佳模型。通过筛选，最终确定3个备选模型，分别是ARIMA(0,1,1)(0,1,1)12、ARIMA(0,1,1)(0,1,2)12、ARIMA(0,1,1)(1,1,0)12，见表1。再利用Box.test函数对3个备选模型进行白噪声检验，计算在滞后阶数6、12处的Ljung-Box统计量，结果见表2。3个模型均通过了白噪声检验，即原始序列中所有信息均被提取充分，所建立的模型有效。3个模型中ARIMA(0,1,1)(0,1,1)12的AIC=39.04，BIC=46.50,均最小，并且各项参数都具有统计学意义，最终确定ARIMA(0,1,1)(0,1,1)12为最佳模型。

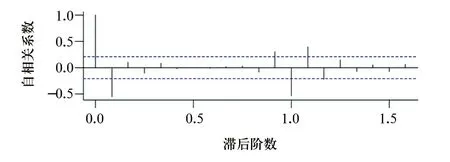
图2 差分后自相关系数图

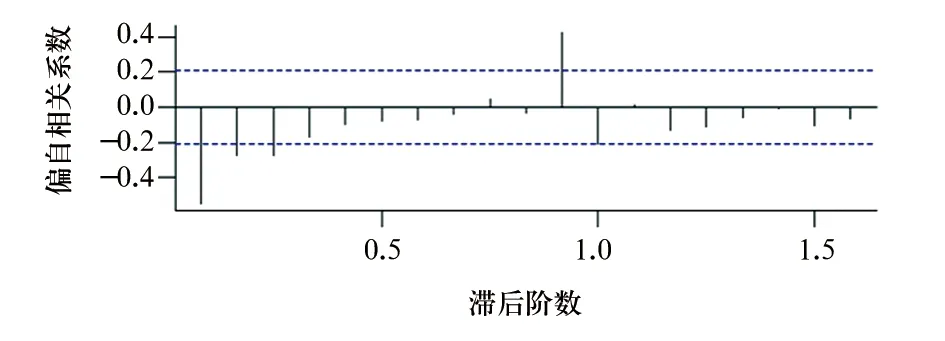
图3 差分后偏自相关系数图

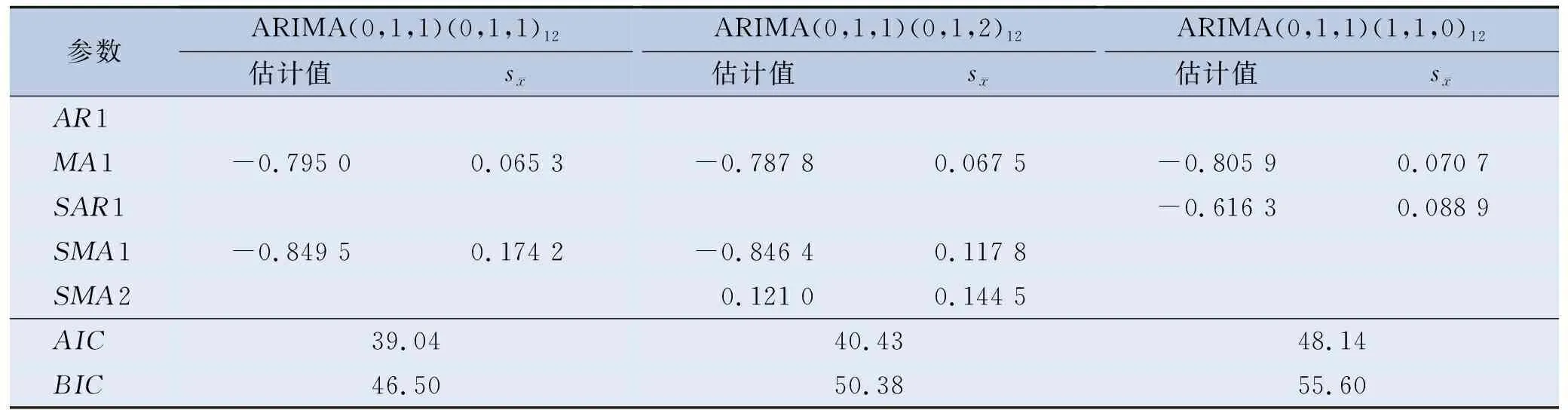
表1 备选模型参数估计

表2 备选模型残差白噪声检验

2.4 模型评价与预测

使用accuracy函数对ARIMA(0,1,1)(0,1,1)12拟合效果进行评价，其MAPE为1.78%，RMSE为0.24。利用建立好的ARIMA(0,1,1)(0,1,1)12模型对2021年7月—2022年5月11个月的平均住院日进行预测，结果见表3、图4。其中2021年8月份的相对误差较大，其他月份的相对误差较小，且所有月份预测值均在95%置信区间之内，RMSE为1.49，MAPE为7.78%，预测结果较为理想。

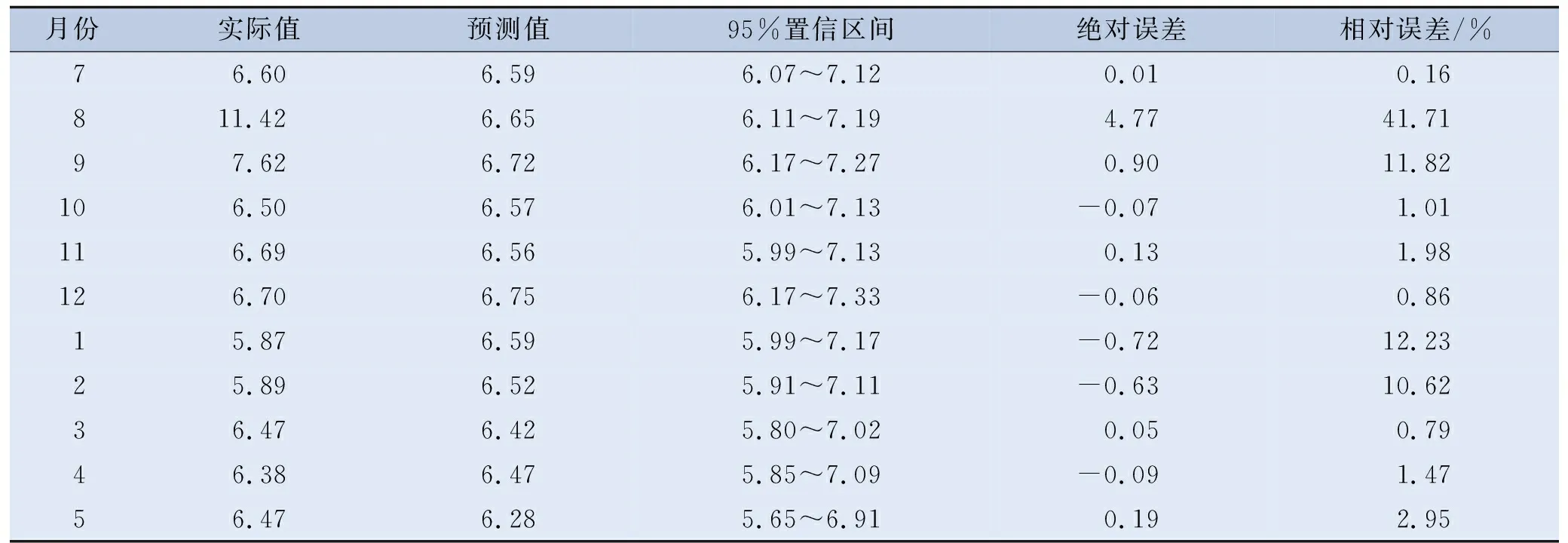
表3 2021年7月—2022年5月平均住院日ARIMA(0,1,1)(0,1,1)12模型预测结果

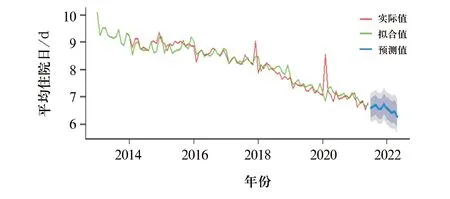
图4 ARIMA(0,1,1)(0,1,1)12模型拟合及预测图

3 讨论

本研究以江苏省某三甲医院为样本医院，建立ARIMA模型对平均住院日进行预测，预测结果总体可靠，为该院平均住院日的预测提供了科学依据，有利于该院合理优化医疗资源配置。

ARIMA模型在建模时综合考虑了趋势因素、周期因素及随机误差等因素的影响，可以很好地对未来一段时间内的平均住院日进行预测。平均住院日的长短，往往也受临床疾病的影响。该院平均住院日整体呈下降趋势，并且在2018年年中下降坡度明显陡峭，可能与该院自2018年7月起成立围手术期管理中心，大力开展日间手术有关。围手术期管理中心集中了入院前的检查、采血化验、预约检查和麻醉评估等4大功能，并对全院的床位实行统一调度使用，加快了床位周转，因此平均住院日得到进一步缩短。从长期数据来看，该院平均住院日呈现递减的时间序列，说明该院医疗质量以及医院运营效率在不断提升。

本研究也存在着一定的局限性。医院平均住院日受诸多方面的影响，如病种、术前待床日、手术占比、床位使用率、三四级手术率等[8]，而ARIMA模型在建模过程中仅依靠历史数据，未能深入分析以上因素对平均住院日的影响。此外，ARIMA模型还忽视了突发事件或公共政策变化带来的影响，如研究中2021年8月份的相对误差较大，当月平均住院日出现显著升高，与当时暴发的新冠肺炎德尔塔病毒疫情明显相关。8月份正值疫情的高发期，严格的疫情管控措施以及核酸检测排查要求，加上转运病人的异常艰难导致病人滞留院中，使平均住院日显著升高。在以后的预测过程中，应加强对医院平均住院日的监测收集，不断更新数据，从而提高预测的准确性和可靠性。