理清问题本质 探究多种解法——2022年武汉市中考数学第9题的解法探究

高武月

(甘肃省庆阳市环县第五中学，甘肃庆阳，745700)

1 试题呈现

(2022年武汉市中考数学第9题)如图1，在四边形材料ABCD中，AD∥BC，∠A=90°，AD=9 cm，AB=20 cm，BC=24 cm.现用此材料截出一个面积最大的圆形模板，则此圆的半径是

图1

( )

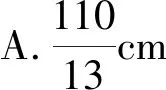
2 试题分析

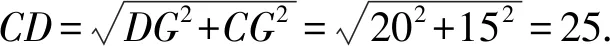
图2

3 解法探究

基于以上分析，本题有多种解法.

思路1利用面积法求解

根据圆的切线的性质，圆的切线垂直于经过切点的半径.因此，本题可以将经过切点的半径作为某些三角形的高线，通过利用面积法列方程求解.

解法1如图3，延长BA，交CD的延长线于点N.⊙I是△BCN的内切圆，切点分别为E，F，H.连接IE，IF，IH，IN，IB，IC.

图3

设⊙I的半径为r，则IE=IF=IH=r.

由S△NBC=S△IBN+S△IBC+S△ICN，得

故选：B.

点评：这种解法将圆与直角梯形ABCD某些边相切问题转化为三角形的内切圆问题，这是学生熟悉的几何模型.通过图形转化，建立起了所求量与已知量之间的逻辑关系，为解决问题创造了有利条件.由此可以看出，面积法是解决三角形内切圆问题的通性通法.

解法2如图4，过点D作DG⊥BC，垂足为G.⊙I与直角梯形ABCD的边AB，BC，CD分别相切于点E，F，H.连接IA，IE，IB，IF，IC，IH，ID.延长FI，交AD于点N.

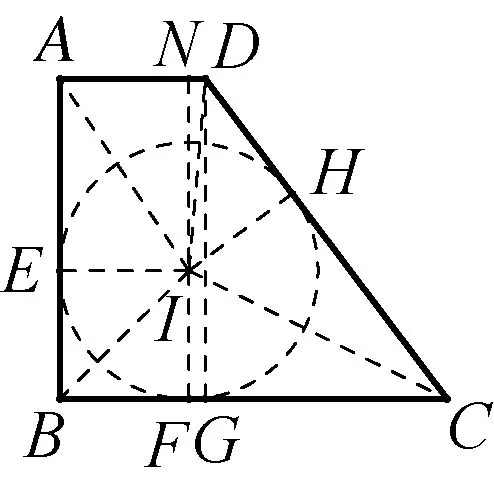
图4

易知DG=AB=20，CG=BC-AD=15，由勾股定理，易得CD=25.

设⊙I的半径为r，则IN=20-r，IE=IF=IH=r.

由S梯形ABCD=S△IAB+S△IBC+S△ICD+S△IAD，得

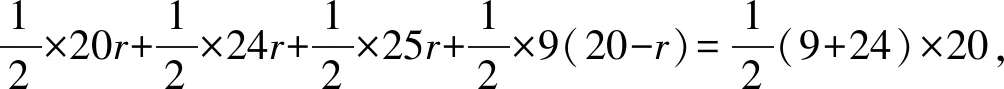
故选：B.

点评：这种解法将直角梯形ABCD分解为四个三角形，然后利用三角形与梯形的面积关系列方程求解.利用这种方法求解的关键是用含有r的代数式表示△IAD的边AD上的高，显然IN=NF-IF=DG-r，故需求得直角梯形ABCD的高DG，既而得到IN=20-r.这种解法主要用到了勾股定理和三角形的面积公式，通俗易懂，是一种较为简洁的解法.

思路2构造相似三角形，利用相似三角形的性质和切线的性质求解

解法3如图5，⊙I与直角梯形ABCD的边AB，BC，CD分别相切，与AB相切于点E，与BC相切于点F，连接IE，IF，IC.过点D作DG⊥BC，垂足为G.过点I作HI∥CD，交BC于点H.

图5

易知DG=AB=20，CG=BC-AD=15，由勾股定理，易得CD=25.

设⊙I的半径为r，则IE=IF=BF=r.

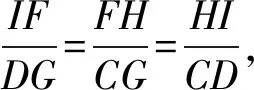
由圆的切线的性质，易知∠DCI=∠FCI.

由IH∥CD，得∠DCI=∠CIH，所以∠FCI=∠CIH.

故选：B.

点评：这种解法构思巧妙，求解过程仅用到了相似三角形的判定与性质、圆的切线的性质、平行线的性质、等腰三角形的性质等知识，所列方程为一元一次方程，求解过程简洁明了，通俗易懂，是一种非常简洁的求解方法.

解法4如图6，⊙I与直角梯形ABCD的边AB，BC，CD分别相切，与AB相切于点E，与BC相切于点F，连接IE，IF，IC.过点D作DG⊥BC，垂足为G.过点D作DH∥IC，交BC的延长线于点H.

图6

易知DG=AB=20，CG=BC-AD=15，由勾股定理，易得CD=25.

由圆的切线的性质，易知∠DCI=∠FCI.

由DH∥IC，得∠DCI=∠CDH，∠FCI=∠H，所以∠CDH=∠H，所以CH=CD=25，所以GH=40.

设⊙I的半径为r，则IE=IF=BF=r.

又因为FC=BC-BF=24-r，所以2r=24-r，解得r=8.

故选：B.

点评：这种解法与解法3类似，也是利用相似三角形的判定与性质、圆的切线的性质、平行线的性质、等腰三角形的性质等知识解决问题，其关键是利用两种不同方法用含有r的代数式表示线段FC的长，然后列方程求解，这本质上是一种“算两次”原理.

思路3构造直角三角形，利用勾股定理列方程求解

解法5如图7，⊙I与直角梯形ABCD的边AB，BC，CD分别相切于点E，F，H.连接IE，IF，IH.过点D作DG⊥BC，垂足为G.延长EI，交CD于点M，过点M作MN⊥BC，垂足为N.

图7

设⊙I的半径为r，则IE=IF=BF=IH=MN=r.

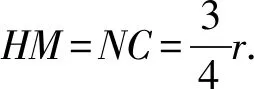
由圆的切线的性质，得HC=FC=24-r.

故选：B.

点评：利用这种方法解决问题的关键是构造合适的直角三角形，用含有r的代数式表示直角三角形的三条边长，然后利用勾股定理列方程求解.这种解法主要用到了相似三角形的判定与性质、全等三角形的判定与性质、圆的切线的性质、勾股定理等知识，这是《义务教育数学课程标准(2011年版)》规定的最基础最核心的知识，是学生必须掌握的内容.由此可以看出，勾股定理是解决与直角三角形有关的线段长度问题的基本工具.

解法6如图8，⊙I与直角梯形ABCD的边AB，BC，CD分别相切于点E，F，H.过点D作DG⊥BC，垂足为G.在⊙I上取点P，使过点P的切线QM∥BC，QM交AB于点Q，交CD于点M，过M作MN⊥BC，垂足为N.

图8

易知DG=AB=20，CG=BC-AD=15，由勾股定理，易得CD=25.

设⊙I的半径为r，则BE=BF=PQ=r，CG=CH=24-r，BQ=MN=2r，AQ=20-2r.

故选：B.

点评：这种解法主要用到了平行线分线段成比例定理、圆的切线的性质、勾股定理等知识，与其他解法相比，这种解法运算量较大，求解过程较为繁琐.

思路4利用解析法求解

解法7如图9，以直线BC为x轴，以直线AB为y轴，建立平面直角坐标系.⊙I与直角梯形ABCD的边AB，BC，CD分别相切于点E，F，H.连接IE，IF，IH，ID.过点D作DG⊥BC，垂足为G.

图9

易知DG=AB=20，CG=BC-AD=15，由勾股定理，易得CD=25.

设⊙I的半径为r，则IE=BF=IF=IH=r，CH=CF=24-r，DH=1+r.

易知I(r，r)，D(9，20).

在Rt△DHI中，由勾股定理，得DH2+IH2=ID2，即(1+r)2+r2=(9-r)2+(20-r)2，解得r=8.

故选：B.

点评：利用解析法求解本题的关键是用含有r的代数式表示△DHI的三条边长.根据切线的性质易得IH=r，DH=1+r.求线段ID的长可利用两点间的距离公式，如果学生不熟悉两点间的距离公式，可通过构造直角三角形，利用勾股定理求解.由此可以看出，解析法也是解决与线段长度有关几何问题的有效工具.

4 结束语

为准确把握问题本质，方便几何问题解决，必须实现已知量与未知量之间的逻辑关系外显化.笔者认为，添加辅助线是实现已知量与未知量之间的逻辑关系外显化的有效手段.在解决与线段长度有关的几何计算问题时，可通过添加辅助线，构造直线三角形、相似三角形、全等三角形或等腰三角形，然后利用这些基本图形的性质求解，必要时可借助一元一次方程或一元二次方程求解.通过“一题多解”，不仅可以提高学生的几何推理能力，而且可以培养学生发散思维和创新思维.面积法和解析法是解决与线段长度有关的几何计算问题的重要方法，有时可起到化繁为简，事半功倍的效果.