函数与方程思想在线性规划中的应用研究

房鹏飞

(安徽省阜南实验中学，安徽阜阳，23600)

1 函数与方程在数学教学中的渗透

关于函数与方程思想方法在数学教学中的渗透，教师不但要考虑学生乐于接受的渗透方式，还需要将其与各阶段的教学目标、教学难度结合起来，设计好函数与方程在数学教学中的渗透深度.为了帮助学生构建协同的函数与方程思想，教师应该注重该思想在教学工作中螺旋上升式、循环渐进式的渗透与应用.

以必修1中解方程的教学为例，在求解方程根时，可借助函数图象与轴相交情况，以此将解方程转变为函数零点求解的问题；以必修5数列教学为例，在求解等差数列问题时，可借助其与特殊函数之间的关系来讲等差数列求解转变为函数求解的问题.再以线性规划问题的教学为例，可将其转变为一定可行域内目标函数求解的问题.在求解更多方程式问题时，教师可利用函数与方程思想方法，将这些方程式转变为函数问题，继而加强方程与函数之间的联系，让学生找到不同知识点的关联点，以此在函数的可行域内去求解函数.

2 线性规划实际教学案例分析

2.1 线性规划中教学难点分析

在线性规划教学中，对于大多数学生而言，求解最优解是一个重难点问题.一些学生不懂最优解在几何上的意义，另一些学生则不能求解最优解.对此，在教学过程中，教师可借助GeoGebra这一多媒体数学教学软件，以动态的方式为学生呈现线性函数，让学生利用数形结合思想，了解线性规划中最优解的几何意义，并提升其分析问题与解决问题的水平.

2.2 学情分析

通过一段时间的学习之后，学生对不等式求解、不等关系等问题已经有所了解，这为后续的建模教学搭建了一定的基础.围绕“利用不等式关系解决线性规划问题”的教学内容，教师可先引导学生对已学的不等式问题进行回忆，再让学生探究不等式在线性规划中的应用价值，并在不等式与线性规划问题之间增加建模思维，让学生借助建模的思想来解决线性规划问题.

2.3 例题解析

银行希望通过为客户提供个人、企业信用贷款来获得收益，而一家银行计划投入的个人、企业信用贷款总额为2 500万元，希望借此实现的收益为3万元.如果该银行通过企业贷款的发放来获得收益的比例为12%，通过个人贷款的发放来获得收益的比例为10%.对此，银行怎样分配其资金才能实现该盈利计划？

教师通过情境教学引出学生设立方程组，继而应用类比法引导学生学会解法，如以函数x-y=6作为边界划分出的两个区域，将区域赋予其不等式的意义.

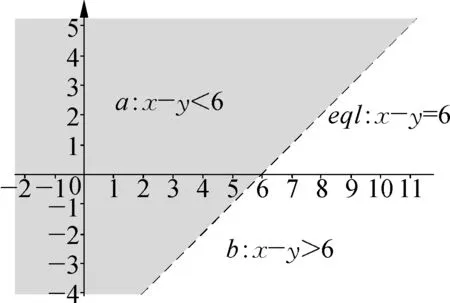
图1 划分区域边界

对于此类问题的求解，教师可先应用GeoGebra这一多媒体数学教学软件，并遵循“画、移、求、答”的基本解题步骤，为学生指出不等式代表的区域、交集可行域，继而为学生讲解不等式在函数中的几何意义，通过滑动画面中的滑动托条来寻找线性规划的最优解，以此解决此类问题.学生在教师的引导下，也可自行识别出函数的可行域，并拖动托条来确立线性函数最优解.

2.4 通过多媒体工具归纳巩固强化运用

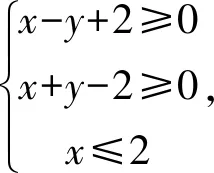
图2 目标函数动画模型

3 函数与方程思想在教学中的应用总结

3.1 通过认真审题了解问题隐含条件

在运用函数与方程思想解决方程问题时，教师应该让学生认真审题，通过审题来把握题目中的隐形条件，从而围绕题目给出的已知条件来搭建解题思路与方法.

例如：已知函数f(x)=xlog2x，g(x)=ax2-x(a∈R)，求f(x)≤g(x)恒成立的实数取值范围.此题的关键在于将函数之间的关系转化为图象之间的关系，要想f(x)0，因为(如图3)对数函数图象x取值范围始终大于0，如果学生没有意识到隐含条件，就无法判断a的取值，因此在解题时，要充分挖掘隐含条件并将其转化利用.

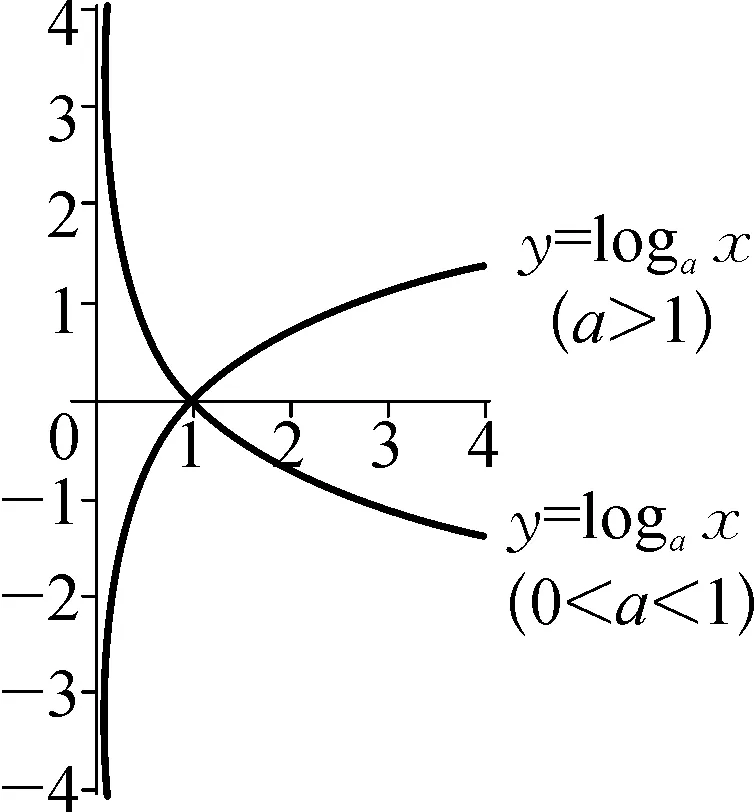
图3 对数函数图象

3.2 通过研究解题思路设立函数模型

认真解读题目后，学生进一步明晰了题目的条件与所要求解的问题，继而需要进一步寻找解题思路.这一过程中，教师可引导学生小组讨论，通过讨论的方式来探究题目中已知量和所要求解未知量之间的联系，基于一定的函数关系、函数原理，借助函数与方程思想为问题设立函数模型，并找到解题思路.如不等式解集条件借助零点存在性定理转化为方程在固定区间内求x1，x2根的问题，充分借助函数模型解决问题.

3.3 利用多重思想实现解决问题

通过审题、解题思路的寻找，继而需要学生结合其他的数学思想方法如建模、分类讨论等将题目中已知条件与未知条件联合起来，应用方程不等式等相关知识原理，借助函数与方程的思想，将方程式求解的问题转化为可行域内函数求解的问题，由此实现解题计划.

通过对题目假设条件的检验、解题过程的归纳总结，以此强化与提升学生对此类问题的求解能力，并让学生更为熟练地应用函数与方程思想方法.

3.4 教学总结

对于函数与方程思想方法的总结，教师不但要结合具体的知识问题来讲解函数与方程思想方法应用范围、重要性，而且应针对类似的题型，提炼与总结函数与方程思想方法的内在规律.在课堂总结、复习阶段，教师可基于横向、纵向两个角度来强调与重申函数与方程思想方法的应用，为了深化该方法在学生实际解题中的应用效果，教师需要本着一定的教学目标，结合具体的方程、函数知识来揭示函数与方程思想的本质.同时，在应用函数与方程思想方法解题时，教师需要结合该思想分散性、层次性的基本特征，坚持螺旋上升式、循环渐进式的应用原则.在一段教学时间之后，尤其是在每个章节结束之后，教师应重新整理各个章节分散的知识点，并认真为学生梳理函数与方程思想方法的应用情形，让学生对函数与方程思想方法的应用规律、情形有良好的认知，加深其对函数与方程思想方法的印象.