基于深度学习的GeoGebra软件与立体几何的教学融合研究

莫宗迪

(中山市龙山中学，广东中山，528471)

在立体几何教学中，视觉思维占了主导地位.对学生的空间思维想象能力要求很高，而学生在学习立体几何的过程中常遇到生活体验有限、空间识别力低、空间形象感知力不足等问题，是高中立体几何教学的老大难问题.笔者通过实践探索得知：教师通过多方位、多维度的探究兼并动手操作，让学生得到多种感官刺激强化，可以有效地提高学生的空间观念，重构正确的空间知识结构，促进学生深度学习.本文以深度学习理论为指导，以“正方体截面情况”为例，探索GeoGebra平台与立体几何融合教学的方法和手段，尝试提供一种立体几何教学的参考.

1 问题的提出

在平时的练习中，我们经常遇到下面这样的题目：

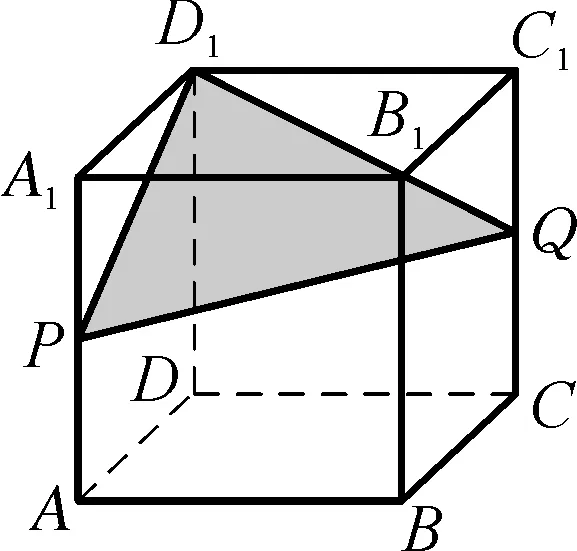
图1

(1) 在棱长为2的正方体ABCD-A1B1C1D1中，如图：P，Q为所在棱的中点，求过三点D1，Q，P的截面面积？

(2) 正方体ABCD-A1B1C1D1棱长为1，P为BC中点，Q为CC1上的动点，过点A，P，Q的平面截正方体所得的截面为S，则下面命题中正确的是

( )

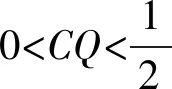
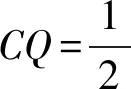
对于这类有关正方体截面的立体几何题，学生的正确率很低，原因在于学生空间思维尚未形成，直观想象不够，空间形象感知力不足.甚至有相当一部分学生直接将过三点的三角形当做截面.一部分学生能通过四点共面的方法找到平面与正方体的截面，但截面情况变化时，仍然受阻.

2 问题分析

初中的平面几何思维到高中的空间思维对学生的认知是一个重大的跨越.学生还没脱离根深蒂固的初中平面几何思维方式，特别是高一的学生，缺乏空间想象力，继而造成空间思维受阻.笔者认为借助实物模型和信息技术可以帮助学生突破空间思维壁障，实现空间问题可视化和直观化.教师可以通过教具和GeoGebra软件的3D功能等工具，引导学生深度学习，实现从抽象到直观的转化，使学生能够轻松地在直观、生动的学习中发展空间思维，形成空间意识和观念.笔者翻阅教材，发现：人教A版的教材中并没有专门针对截面情况的课时.只对四点共面的证明作了要求.学生的空间感知力的提升需要教师引导学生亲身通过实验操作或空间思维“可视化”的展示，在潜移默化中培养了学生的空间想象力和观察力.

3 解决问题

深度学习理论认为：学生的深度学习是对知识的深度理解、由低阶思维转化为高阶思维、实现知识的迁移和实践创新的学习过程[2].

3.1 让学生经历由低阶思维转化成高阶思维

笔者借助实物模型让学生建立二维与三维的联系，感知空间实物的形态与变化.

准备材料：正方体模型框架、绳子和双面胶、电池、泡沫正方体模型、电热丝和自制的切割装置.

问题1：如果我们拿一个平面去截一个正方体那么会得到什么形状的截面图形呢？

动手操作1：用电热丝切割正方体泡沫模型，如下图2和图3.

图2

图3

设计意图：通过学生自己动手操作，了解截面形成过程.使学生对正方体的截面情况有了初步的图象表征，在大脑中有了大致的空间观念.

动手操作2:用绳子捆绑正方体模型，观察绳子形成的截面情况？

设计意图：通过红绳捆绑正方体模型体验截面的变化，总结截面出现的情况，以及出现的弊端.然由捆绑绳子形成截面很容易出现偏差，因为绳子捆绑的可能不是一个面，可能仍是空间图形.但学生在亲身经历截面形成的过程中初步构建了空间观念.

学生通过自己的动手操作，调动了各种感官，多方位、多角度观察、认知事物，进而获得更清晰、牢固的空间观念.通过实验操作活动，可以帮助学生准确想象出几何图形形成现实空间.通过实例进化思维，把空间中的实体高度抽象在大脑中，并在大脑中进行分析推理.这种方法提高了学生动手能力，提高了学生主动探索的意识，是培养空间想象力的一个有效途径.

3.2 对空间知识的深度理解实现知识迁移

笔者借助信息技术GeoGebra平台，制作正方体截面的动态课件.通过对滑动条的平移操作实现对截面的平移、翻转，直接将所得的截面可视化，与动手操作得到的空间观念形成对比，纠正学生的错误认知，重新建构学生的空间知识结构.

问题2：截面如果是三角形，有几种情况？

学生通过切割模型和绳子捆绑讨论研究，老师协作引导探究.用GeoGebra软件进行信息技术的准确截面分析(如图4).

图4

设计意图：教具操作有很多情况是不能展示的，借助信息技术GeoGebra软件通过3D的空间图形形式，更直观地展示截面各种出现的情况.

问题3：如果截面是四边形，可以截出什么形状的四边形？

问题4：能截出五边形，六边形吗？

问题5：能截出七边形吗？

问题6：截面多边形的边数最多有几条？

设计意图：通过学生的动手操作和空间想象，找学生代表发言总结；利用软件平台直接反馈纠正，形成正确的数学认识、数学知识.

GeoGebra软件的3D绘图功能，直观、生动、形象的教学诱发学生展开丰富的联想，鼓励学生大胆猜想，让学生真实地经历数学立体几何问题的产生和解决全过程，既为思维的展开创造了良好条件，也为空间观念的顺利形成打开了大门.

图5

借助信息技术GeoGebra软件、一体机多媒体平台，很直观地演示各种情况下正方体分截面情况，使得学生体验到由抽象到具体形象，便于理解，认清本质.特别是用GeoGebra动态演示，使学生突破了认知难点：过棱上三点的平面与正方体表面的交线围成的截面情况.学生往往认为过三点的平面是三角形.其实面是无限的，通过操作GeoGebra软件的平移、翻转等完成截面的形成，纠正学生的错误认知，重新建构学生的空间知识结构.笔者通过总结提炼得出Geogebra软件与立体几何融合教学探究流程，如下图6.

图6 GeoGebra软件与立体几何融合教学探究流程

4 应用推广

GeoGebra对立体几何教学的一个重大功能是：帮助学生直观化、可视化地突破认知难点.顺利地将试卷上呆板的图形更立体、生动地呈现给学生看，构建新的空间知识，最终培养学生问题解决、知识迁移和创新的能力.

图7

例1已知正方体的棱长为4，如图，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为多少？

学生往往比较困惑为何在各棱中点时，截面取得最大值？笔者借助GGB软件的动态展示以及截面面积的动态变化分析，大大加强了学生的直观感受.教师再进行推理证明计算.学生受到的感官刺激更大，理解更透彻而且能激起学生探索的积极性.

5 结论与展望

现代心理学研究表明，表象的获得在于对实物的感知，特别是视觉感知.感知的多样性直接影响着获得表象的多样性.笔者认为在立体几何的教学中，教师应对学生进行多方位和多维度的感官刺激，建构学生的空间感知力，使学生对知识能深度理解，进而达到知识迁移和实践创造能力.鼓励教师在课堂上采用学生动手操作、教具模型操作和GeoGebra平台动态演示等多种手段结合.当然立体几何模型是有限的，但是强大功能的GeoGebra软件平台与立体几何的融合就很有必要了，它能呈现以往教学中难以呈现的课程内容，能够调动学生各种感官，多方位、多角度观察、认知事物，获得更清晰、牢固的空间观念，实现直观想象素养！